|
김관석
|
2020-05-13 13:43:29, 조회수 : 569 |
- Download #1 : 11_b.jpg (112.4 KB), Download : 1
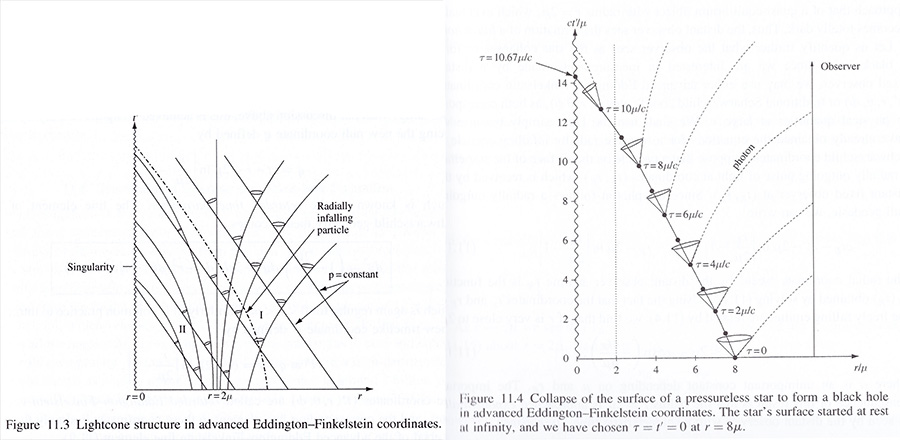

11.5 Eddington-Finkelstein coordinate (Eddington-Finkelstein 좌표)
Figure 1.11 과 11.2 의 시공간 diagram들은 방사상으로 움직이는 photon들과 질량의 입자들 모두의 세계선들이 𝑟 = 2𝜇 를 𝑡 = ∓∞ 에서 넘는 것을
보여준다. 이것은 '직선' 𝑟 = 2𝜇, -∞ < 𝑡 < ∞ 가 실제로는 한 직선이 전혀 아니고 한 단일한 점일 수도 있음을 제시한다. 즉, 우리의 좌표가 한 단일한
사건을 전체 직선 𝑟 = 2𝜇 으로 확장한 데가 잘못될 수 있는 것이다. 불만족한 좌표의 문제를 우회하기 위한 한 기법은 측지선으로 시공간을 '탐사하기'
로서, 측지선들은 결국 좌표와 독립되고 또한 좌표 유효성의 경계들에 의해서 아무런 영향을 받지 않을 것이다. 많은 가능성 중에서 우리는 탐사기로서
방사상으로 움직이는 photon의 세계선을 사용할 것이다.
Advanceded Eddington-Finkelstein Coordinate (전진한 Eddington-Finkelstein 좌표)
특히 우리가 낙하하는 입자들의 한 개선된 기술을 개발하기를 바라기 때문에, 우리는 방사상으로 낙하하는 photon들을 바탕으로 한 새 좌표계를 구성함
으로써 시작하도록 한다.방사상으로 들어오는 photon의 세계선은 다음으로 주어짐을 기억하라.
𝑐𝑡 = -𝑟 - 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣ + constant,
그 수법은 적분 상수 를 우리가 𝑝로 표시하는 새 좌표로 사용하는 것이다. 이리하여, 우리는 다음의 그 좌표 변환을 만든다.
𝑝 = 𝑐𝑡 + 𝑟 + 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣, (11.5)
여기서 𝑝는 역사적인 이유로써 advanced 시간 매개변수 로 알려졌으며, 그것은 분명히 null 좌표이다. 𝑝는 방사상으로 들어오는 photon의 전 세계선을
따라 상수이므로, 그것은 그 세계선이 어디를 관통하든 한 '좋은' 좌표일 것이다.
(11.5)를 미분하면 다음을 얻는다.
𝑑𝑝 = 𝑐 𝑑𝑡 + 𝑟/(𝑟 - 2𝜇) 𝑑𝑟,
그리고, Schwarzschild 선형 요소들에서 𝑑𝑡를 치환하면, 우리는 매개변수 𝑝의 용어로 그 선형요소들이 다음의 단순한 형식을 취함을 발견한다.
𝑑𝑠2 = (1 - 2𝜇/𝑟) 𝑑𝑝2 -2𝑑𝑝𝑑𝑟 - 𝑟2(𝑑𝜃2 + sin2𝜃𝑑𝜙2). (11.6)
우리는 즉시 (11.6)으로부터 𝑑𝑠2가 이제 정칙적 (regular)이라는 것을 본다; 과연 그것은 한 낙하하는 photon의 측지선에 의해서 탐사된 𝑟-값의 범위인,
전 0 < 𝑟 < ∞ 범위에서 정칙적이다. 이렇게, 어떤 점에서, 그 변환 (11.5)는 복합 함수의 해석적 연속 을 연상시키는 한 방법으로 그 해의 좌표 범위를
연장시켰다.
(이하는 좀 간추려 기술함 ...) 그 metric (11.6)은 null 측지선의 경로를 계산하는데 편리해서, (𝑑𝑠 = 𝑑𝜃 = 𝑑𝜙 = 0 이므로) 다음으로 주어진다.
(1 - 2𝜇/𝑟)(𝑑𝑝/𝑑𝑟)2 - 2𝑑𝑝/𝑑𝑟 = 0,
그것은 다음의 두 해를 갖는다.
𝑑𝑝/𝑑𝑟 = 0 ⇒ 𝑝 = constant; 𝑑𝑝/𝑑𝑟 = 2(1 - 2𝜇/𝑟) -1 ⇒ 𝑝 = 2𝑟 + 4𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣ + constant, (11.7)
이들은 각각 들어오고 나가는 방사적 null 측지선들에 대응한다. 그런데 𝑝가 null 좌표라는 것이 직관적으로는 친숙하지 않으므로, 다음으로 정의되는
그와 관련된 timelike 시간 좌표 𝑡'로 실행하는 것이 일반적이다.
𝑐𝑡' ≡ 𝑝 - 𝑟 = 𝑐𝑡 + 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣. (11.8)
𝑑𝑠2 = 𝑐2(1 - 2𝜇/𝑟) 𝑑𝑡'2 - (4𝜇𝑐/𝑟)𝑑𝑡'𝑑𝑟 - (1 + 2𝜇/𝑟)𝑑𝑟2 - 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2). (11.9)
좌표 (𝑡', 𝑟, 𝜃, 𝜙)는 advanced Eddington-Finkelstein 좌표라고 불린다. 우리는 여기서 변환 𝑡' → -𝑡' 에 대해 불변적이지 않음에 주목한다. (11.7)
로부터, 우리는 들어오고 또한 나가는 photon 세계선들이 다음으로써 주어짐을 본다.
𝑐𝑡'= -𝑟 + constant, (11.10); 𝑐𝑡'= 𝑟 + 4𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣ + constant, (11.11)
들어오는 photon을 위한 𝑟-축에 45∘ 각을 이루는 직선에 대응하는 첫번째 방정식은 0 < 𝑟 < ∞ 를 위해서 유효하고, 이 photon 측지선들은 𝑟 = 2𝜇 를
가로질러 연속된 직선들이다. 이 좌표에서 Schwarzschild 기하학의 시공간 diagram은 위 Figure 11.3 에서 보여진다. 그 시공간 diagram은 이제 더
상식적이다. 한 떨어지는 방사상 궤적이나 photon은 Schwarzschild 반경 𝑟 = 2𝜇에서 연속적이다. 광추 구조가 Schwarzschild 반경에서 바뀌어 일단
당신이 그 경계 𝑟 = 2𝜇 를 넘으면 당신의 미래는 그 특이점으로 향한다, 유사하게, 한 입자나 photon이 𝑟 < 2𝜇 에서 시작하면 𝑟 > 2𝜇 으로 탈출할 수
없다. Schwarzschild 반경은 한 사건 지평선 돌아오지 않는 경계를 정의한다. 일단 한 입자가 그 사건의 지평을 넘으면 그것은 그 특이점 𝑟 = 0 으로만
떨어져야만 한다. 더구나, '나가는' null 측지선들의 경로에서는, 우리는 𝑟 < 2𝜇 에서 떨어지는 입자에 의해서 방출된 어떤 photon들도 영역 𝐈 에 있는
관찰자에 도달하지 않을 것이다. 이렇게 그 입자는 그러한 관찰자에게는 그 사건 지평선을 건널 수 없는 것처럼 보인다, 한 사건 지평선을 갖고 있는 한
compact한 물체는 블랙홀 (black holes)이라 불린다.
Retarded Eddington-Finkelstein Coordinate (지연된 Eddington-Finkelstein 좌표)
이번에는 누가 방사적으로 나가는 photon들의 세계선을 바탕으로 한 새 좌표계를 구성한다면 어떻게 되나고 묻는 것은 합리적일 수 있겠다. 앞에서의
과정과 유사하게 진행하면서 다음으로 정의된 새 null 좌표 𝑞를 도입함으로써 곧바로 이를 성취할 수 있다.
𝑞 = 𝑐𝑡 - 𝑟 - 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣,
이것은 지연된 시간 매개변수 로 알려져 있다. 그러면 Schwarzschild 기하학의 선형 요소 다음이 된다.
𝑑𝑠2 = (1 - 2𝜇/𝑟) 𝑑𝑞2 + 2𝑑𝑞𝑑𝑟 - 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2),
이것은 또다시 0 < 𝑟 < ∞ 에서 정칙적이다, 유사하게, 다음으로 정의되는 timelike 좌표 𝑡*를 도입하는 것이 일반적 실행이다.
𝑐𝑡* ≡ 𝑞 + 𝑟 = 𝑐𝑡 - 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣.
좌표 (𝑡*, 𝑟, 𝜃, 𝜙)는 retarded Eddington-Finkelstein 좌표라 불리며, 이 좌표의 선형 요소들은 단순히 advanced Eddington-Finkelstein 좌표 선형
요소 (11.9)의 시간 반전(time reversal)이다.
Figure 11.3 에 유추된 retarded Eddington-Finkelstein 좌표로 시공간 diagram를 그리는 것은 수월해서, 우리는 나가는 방사적 null 측지선들은
𝑟-축에 45∘ 각을 이루지만, 반면에 들어오는 null 광선들은 비연속적이며, 𝑟 = 2𝜇 에서 𝑡* = +∞ 로 향함을 본다. 이 경우에, 표면 𝑟 = 2𝜇 이 또다시 한
일방향의 membrane으로 작용하지만, 그러나 이 시간은 오직 나가는 timelike 또는 null 측지선만이 내부에서 외부로 넘도록 허용한다. 과연, 입자들은
𝑟 = 0 의 특이점으로부터 움직여 나가야만 하고 그래서 𝑟 < 2𝜇 영역으로부터 강제로 내쫓긴다. 그러한 물체는 한 화이트홀 (white hole) 이라 불린다.
이 거동은 한 massive한 물체의 중력적인 인력을 고려하는 우리의 직관에는 완전히 어긋난 듯하다. 더구나, 우리는 좌표들이 시공간 사건들의 단지
임의적인 label들이라는 입장을 줄곧 유지 해온 까닭에, 어떻게 이 물리적 과정이 좌표의 선택에 의존해서 그렇게도 과격하게 다르게 일어나는 것일까?
그 명백한 paradox를 해결하는 열쇠는 우리의 원래 좌표 (𝑡, 𝑟, 𝜃, 𝜙)가 '전체의' Schwarzschild 기하학의 일부만 담당했다는 것을 깨닫는 것이다. 이
topic은 전체 기하학을 포함하고 또한 한 블랙홀과 한 화이트홀의 양자 특이점을 소유하는 것을 보여주는 Kruskal 좌표를 도입하는 Section 11.9에서
충분히 논의돤다. (수학적인 호기심에 반하여) 물리적 실재로의 화이트홀들은 상당히 의심스럽지만, 우리가 이제 논의하려고 하는 것처럼, 블랙홀들은
물리적으로 발생할 것 같다.
11.6 Gravitational collapse and black-hole formation (중력의 붕괴와 블랙홀 형성)
우리의 블랙홀의 특성에의 조사가 대자연에 존재할 수 있다고 믿지 않는다면, 크게는 academic하다고 하겠다. 그것들의 존재 가능성은 중력의 붕과의
관념으로부터 발생한다.
하나의 별은 그 질량에 의존하는 상대적인 공헌들(relative contributions)인 gas와 방사능 압력(rdiation pressure)의 한 혼합체에 의해 유지된다. 이
압력 지지(pressure support)를 공급하는 energy는 가벼운 핵들이 무거운 것들로, 현저하게는 helium 원자 각 하나당 약 26Mev를 방출하면서 수소가
helium으로 융합하는 데서 비롯된다. 하지만 그 모든 핵 연료가 전부 사용되면, 그 별은 냉각되고 또한 자신의 중력햐에서 붕괴하기 시작한다. 대부분의
별들은, 그 붕괴가 한 백색왜성 (white dwarf)이라고 알려진 한 고밀도 별 잔존물(stellar remnant)에서 끝이 난다. 실제로, 약 50억년이 지나면 태양은
붕괴하여 약 5000km 반경이고 또한 약 109kgm-3인 높은 평균 밀도의 한 백색 왜성을 형성할 것이다.
천문학지들은 1915년 (Sirius B로 알려진 가장 이른 예) 같은 오래전부터 백색왜성들에 관하여 알고 있었으나, 아무도 그것들을 어떻게 설명할 지 알지
못했다. 내부 압력이 그렇게 고밀도의 물체를 지지하는 물리적 장치는 한 신비였다. 그 해답은 양자역학의 발전과 Fermi-Dirac 통계의 형성을 기다려야
했다. Fowler는 1926년 이 백색왜성들이 전자 축퇴 압력 (electron degeneracy pressure)에 의해 유지되는 것을 깨달았다. 한 백색왜성에 있는 전자
들은 한 금속안의 자유 전자들과 같이 거동하지만, 백색-왜성 형태안의 그 별의 작은 크기 때문에 그 전자 상태들은 energy 안에서 넓게 간격하고 있다.
Pauli 배타 원리로 인해서 그 전자들은 한 높은 특성의 Fermi energy에까지 완전히 그 상태들을 채운다. 그 별의 붕괴로부터 구하는 것은 이 높은 전자
energy인 것이다.
1930년, Chadrasekhar는 한 백색왜성이 더 massive할 수록 더 고밀도가 되고 따라서 그 중력장이 더 강해짐을 깨달았다. 약 1.4𝑀⊙의 한 임계 질량를
넘는 백색왜성에게는, 중력은 그 축퇴 압력을 압도하고 또한 아무론 안정적 해가 가능하지 않게 되곤 한다. 이리하여, 그 물체의 중력의 붕괴는 계속되어
야만 한다. 처음에는 그 백색오ㅔ서이 한 점으로 붕괴함이 틀림없다고 생각되었으나, 중성자의 발견 후에는, 그렇지만, 그 붕괴의 어떤 단계에서 지극히
높은 고밀도들이 전자들이 역 𝛽-붕괴를 경유해서 중성자들(그리고 단순히 탈출하는 neutrio들)이 양성자들과 상호작용을 하도록 초래함을 깨닫게 되었다.
그러므로 축퇴된 중성자들에 의해서 압력 지지를 공급받은 하나의 새로운 안정적인 구성 - 한 중성자별 - 이 가능하다. 한 태양 질량의 한 중성자별은 약
1016kgm-3 밀도와 더불어서 단지 30km의 반경을 갖는다. 한 중성자별안의 물질은 핵의 밀도(nuclear density)에 있으므로 그 별의 중력의 힘들은 지극히
강하다. 실제로, 한 성상 물체의 진화에서 일반상대성적 효과가 중요하다고 (Chapter 12에서 상대론적 별들을 논의할 것이다) 예상되는 첫번째 점이다.
한 중성자별 내부에서 극한 밀도가 주어지면 물질의 상태 방정식 안의 불확실성들이 남는다. 그럼에도 불구하고, (백색왜성에게는) 그 위로는 안정적인
중성자-별 구성이 가능하지 않은 한 최대 질량이 존재한다고 믿어진다. 이 최대 질량은 약 3𝑀⊙ (Openheimer-Volkoff 한계라고 알려진)이라고 믿어진다.
이렇게, 우리는 이 한계보다 더 질량이 큰 별들은 붕괴하여 블랙홀 을 형성한다고 믿는다. 나아가 만일 그 붕괴가 구면으로서 대칭이면 그것은 반드시 한
Schwarzschild 블랙홀을 생기게 한다.
일부의 이론가들은 블랙홀의 형성에 대해 대단히 회의적이다. Schwarzschild 해는 특별히 대단히 특별하다 - 그것은 구형으로서 정확하게 구면인
대칭이다. 현실에서는, 헌 별은 완벽하게 대칭적이 않고, 그래서 아마도, 그것이 붕괴하면서 그 비대칭이 확대되면서 또한 한 사건 지평선이 생기는 것을
막는다. 그렇지만 1960년대 초에 Penrose는 '특이점 정리들'의 한 유명한 순열을 증명하기 위해 광범위한(global) 기하학적 기법들을 적용했다. 이들은
실제 상횡에서 한 사건 지평선 (한 닫혀진 덫의 곡면)이 형성되고 또한 이 곡면안에 한 특이점, 즉 곡률이 발산하고 그래서 일반상대성이 유효하지 않게
되는 한 점이 틀림없이 존재한다는 것을 보여주었다. 이 특이점 정리들은 블랙홀이 대자연에 반드시 형성하는 것을 사람들에게 설득하는 데에 중요했다.
우리는 블랙홀이 과연 존재한다는 어쩔 수 없는 증거가 있음을 볼 것이다. 더구나, 강력한 X-ray 망원경들을 사용해 몇년내로 블랙홀들의 질량을 측정할
뿐만 아니라 그 각 운동량들도 측정할 수 있게 되야 마땅하다! 강한-중력 체재(regime)의 직접 실험적 탐사가 이제는 가능하다.
11.7 Spherically symmetric collapse of dust (먼지의 구상적인 대칭적 붕괴)
우리가 한 massiv한 별의 구상적인 대칭적 붕괴가 한 Schwarzschild 블랙홀을 형성하고 또한 이 과정이 먼 반경에 있는 고정된 관찰자에 의해서 보여
지는 이 과정을 고려하도록 하라. 단순하게, 우리는 그별이 한 균일한 밀도를 갖고 또한 내부 압력은 영으로 가정한 경우를 고려한다. 그것들의 운동을
구부러뜨리는 압력 구배의 부재에서는 이 '먼지의 공'의 바깥 곡면에 있는 입자들은 단순히 방사적 측지선을 따를 것이다. 우리의 분석을 아직 더 단순화
하기 위해서, 우리는 처음에는 그 '별'의 표면-곡면-이 무한에서 정지해 있다고 가정할 것이다. 이 경우에는 그 곡면의 입자들은 방사적인 측지선을 따를
것이다.
구상형 별의 중력의 붕괴에 참여하는 두 관찰자를 고려하라. 한 관찰자는 그 별의 곡면을 𝑟 = 0 까지 올라타고, 또한 다른 관찰자는 커다란 반경에서
고정되어 남아있다. 게다가 그 추락하는 관찰자는 한 시계를 갖고서 먼 관찰자와 이 시계에 따른 동일한 간격으로 방사적인 광신호들을 보냄으로써 연락
한다고 가정하라. Figure 11.4는 𝜃와 𝜙가 은폐된 advanced Eddiington-Finkelstein 좌표 (𝑐𝑡', 𝑟) 의 관련된 시공간 diagram을 보여준다. 그 점들은
𝑐𝑡/𝜇 의 단위 간격들을 나타내고 또한 우리는 𝑟 = 8𝜇 에서 𝜏 = 𝑡' = 0 를 선택했다. 이 diagram은 Figure 11.2 로부터의 결과들로부터 쉽게 구축된다.
고정된 𝑟에의 한 원거리 관찰자에게는, 우리는 표준 Schwarzschild 좌표 시간 𝜏는 고유시간을 측정한다는 것을 안다. 하지만 우리는 (11.8)로부터 𝑟이
고정되면 𝑑𝑡' = 𝑑𝑡 이라는 것을 본다. 이리하여, 𝑡'의 한 단위 간격은 한 원거리 관찰자의 고유시간의 단위 간격에 대응한다. diagram으로부터, 우리는
그 빛 파동이 𝑡'의 동일한 간격으로 수신되지 않음을 본다. 오히려, 원거리 관찰자에 의해 측정되는 파동간의 고유시간 간격은 끊임없이 증가한다. 과연,
이 관찰자에게 도달하는 마지막 빛 파동은 그 별의 표면이 𝑟 = 2𝜇 를 넘기 바로 전에 방사된 것이다. 이 photon의 세계선은 단순히 수직선 𝑟 = 2𝜇 이고,
그래서 이 파동은 그 원거리 관찰자에게는 𝑡' = ∞ 로 '도달할' 뿐이다. 그 별의 표면이 그 사건의 지평선을 건너간 후에 방사된 파동은 더 큰 𝑟이 아니고
대신에 더 작은 𝑡로 진행하고 또한 𝑟 = 0 에의 특이점에서 종료한다.
이처럼, 원거리 관찰자는 별의 표면이 반경 𝑟 = 2𝜇 을 건너는 것을 결코 보지 못한다. 더욱이, 떨어지는 관찰자의 시계에 의해 똑깥은 간격으로 방사된
파동들은 점점 더 먼 간격들로 원거리 관찰자에게 도착한다. 결과적으로, 그 원거리 관찰자에 의해 수신된 photon들은 점점 더 적색편이가 되고, 그 적색
편이는 별 표면이 𝑟 = 2𝜇 에 도달하면 무한으로 향한다. 이 양자 효과들은 원거리 관찰자는 별의 광도가 영으로 떨어지는 것을 보는 것을 의미한다. 요약
하면, 그 원거리 관찰자는 붕괴가 느려지고 또한 별 상태가 반경 𝑟 = 2𝜇인 한 유사-평형(quasi-equilibrium) 물체의 것으로 접근하는 것을 본다. 이렇게,
원거리 관찰자는 한 블랙홀 의 형성을 본다. /
앞으로 우리는 그 관찰자가 그 별이 붕괴하여 한 블랙홀을 형성하는 것을 본 것을 정량화하도록 한다. (이제부터는 요약해서 기술하기로 한다.) 우리는
advanced Eddington-Flinkelstein 좌표와 전통적 Schwarzschild 좌표를 사용한다, 별의 표면의 한 입자는 좌표 (𝑡𝐸, 𝑟𝐸) 에서 방사적으로 나가는 빛의
파동을 방사하고, 그것은 (𝑡𝑅, 𝑟𝑅) 에의 고정된 원거리 관찰자가 수신한다고 가정하라. 그 photon은 한 방사적으로 나가는 null 측지선을 따르기 때문에,
다음으로 쓸 수 있다.
𝑐𝑡𝐸 - 𝑟𝐸 - 2𝜇 ln ∣ 𝑟𝐸/2𝜇 -1∣ = 𝑐𝑡𝑅 - 𝑟𝑅 - 2𝜇 ln ∣ 𝑟𝑅/2𝜇 -1∣. (11.2)
(11.4)에 의한 𝑡𝐸와 𝑟𝐸의 관계 사실을 사용해서, 만일 𝑟이 2𝜇에 매우 접근하면,
𝑟𝐸(𝑡𝑅) ≈ 2𝜇 + 𝑎 exp(-𝑐𝑡𝑅/4𝜇), (11.13)
여기서 𝑎는 𝜇와 𝑟에 의존하는 중요하지 않은 상수이다. (그 과정은 해설되지 않음) 이 결과의 중요성은 𝑟 = 2𝜇 가 원거리 관찰자에게 한 특성화된 시간
4𝜇/𝑐와 더불어서 지수적으로 접근된다는 것이다. 다음에 의해서
𝜇/𝑐 = 𝐺𝑀/𝑐3 = 5 ⨯ 10-6 (𝑀/𝑀⊙) seconds,
이므로, 별-크기의 물체를 위한 그 시간 축척은 보통 천체물리학적 표준보다는 아주 작다. 이처럼 임의의 붕괴를 위한 블랙홀로의 접근은 지극히 빠르다.
시간 𝑡의 한 함수로서 원거리 관찰자에 의해서 보여지는 적색편이를 작업해보도록 한다. 그 방사와 수신에서의 photon의 그 주파수의 비율은
𝜈𝑅 / 𝜈𝐸 = 𝑢𝜇𝑅 𝑝𝜇(𝑅) / 𝑢𝜇𝐸 𝑝𝜇(𝐸), (11.14) [Eq. (9.52) 참조]
여기서 𝑢𝐸와 𝑢𝑅은 각각 방사자와 수신자의 4-velocity들이고 또한 𝑝는 photon 4-momentum이다. 그 별의 표면에 탄 방사자의 4-velocity는
[𝑢𝜇𝐸] = [(1 - 2𝜇/𝑟)-1, -(2𝜇𝑐2/𝑟)1/2, 0, 0], [Eq. (9.38, 39) 참조]
한편으로는 무한대에서의 고정된 관찰자의 4-velocity는 (𝑟 → ∞ 를 대입하면)
[𝑢𝜇𝑅] = [1, 0, 0, 0].
그러므로 (11.4)는 다음으로 정리된다.
𝜈𝑅 / 𝜈𝐸 = 𝑝0(𝑅) / 𝑢0𝐸 𝑝0(𝐸) + 𝑢1𝐸 𝑝1(𝐸) = [𝑢0𝐸 + 𝑝1(𝐸)/𝑝0(𝐸) 𝑢1𝐸]-1,
여기서 우리는 Schwarzschild metric이 고정적이고 또한 그래서 photon 측지선을 따라서 𝑝0가 보존된다는 사실을 사용했다. 더욱이, 𝑝은 null이므로
우리는 𝑔𝜇𝜈𝑝𝜇𝑝𝜈 = 0 을 필요로 하여, 그것은 이 경우에는 다음으로 정리되어,
1/𝑐2(1 - 2𝜇/𝑟)-1(𝑝0)2 - (1 - 2𝜇/𝑟) (𝑝1)2 = 0.
그래서, 방사적으로 나가는 photon에서는, 𝑝1 = -(1 - 2𝜇/𝑟)𝑝-1𝑝0/𝑐 그리고 다음을 발견한다.
𝜈𝑅 / 𝜈𝐸 = (1 - 2𝜇/𝑟)[1 + (2𝜇/𝑟)1/2]-1 = 1 - (2𝜇/𝑟)1/2. (11.15)
𝑟 → 2𝜇 이면 우리는 𝜈𝑅 → 0 가 되며 그래서 (진동수에 반비례하는 파장의) 적색편이가 무한임을 본다. 𝑟 = 2𝜇 부근에서 (11.15)를 Taylor 확장을
하면, (근사식을 구하기 위해서), 우리는 다음으로 쓸 수 있다. (그 유도 과정은 생략한다)
𝜈𝑅 / 𝜈𝐸 ≈ (𝑟 - 2𝜇)/4𝜇;
그렇지만, 사건 지평선 부근에서 수신의 시간은 (11.13)에 의해 주어 진다. 그래서
𝜈𝑅 / 𝜈𝐸 ∼ exp(-𝑐𝑡/4𝜇), (위는 근사치이고, 이것은 유사치임)
그래서 그 적색편이는 한 특성화 시간 4𝜇/𝑐와 더불어 무한대로 지수적으로 증가한다. 그 광도(luminosity)의 계산은 비방사적인 photon 측지선도 포함
하기 때문에 더욱 복잡하다. 그럼에도 불구하고, 위의 분석을 통해서 우리는 계속적인 photon들 간의 간격이 또한 ∼ exp[-𝑐𝑡/4𝜇]으로 감소함을 보고
또한 우리는 그 광도가 ∼ exp[-𝑐𝑡/2𝜇]으로 지수적으로 약해지는 것을 예측한다.
11.8 Tidal forces near a black hole (한 블랙홀에 가까운 조석력)
Newton적 중력에서 지구를 향해서 자유 낙하는 상호 작용하지 않는 입자들의 한 분포(distribution)-한 집합체-는 중력의 조석 효과에 의해서, Section
(7.14)에서 논의되었듯이, 운동의 방향으로는 늘어나고 가로지르는 방향으로는 압축될 것이다, 똑같은 효과가 일반상대성에서 한 구형 물체를 향해서
떨어지는 한 신체(body)에서도 일어나는데, 만일 그 물체가 한 블랙홀이면 그 효과는 r = 0 에서 무한대가 된다.
우리는 그 조석력을 전통적 좌표 (𝑡, 𝑟, 𝜃, 𝜙)의 Schwarzschild 기하학으로 계산할 수 있다. 공간의 임의의 점에서, 자유 낙하하는 조석력은 임의의
(근접한) 입자의 짝들을 위해서 같은 형식을 갖는다. 그래서, 𝑟에서 정지함으로부터 해제된 두 입자의 경우에서 어떤 좌표 반경 𝑟에서의 조석력을 계산
하는 것이 가장 쉽다. 이 경우, 그 입자들 중 하나의 순간적으로 정지한 관성적 계를 정의하는 한 직교(orthonormal) 기저 vector들의 계는 다음과 같이
취할 수 있다.
(ȇ0)𝜇 = (1/𝑐)𝑢𝜇 = (1/𝑐)(1 - 2𝜇/𝑟)-1/2𝛿𝜇0, (ȇ1)𝜇 = (1 - 2𝜇/𝑟)1/2𝛿𝜇1, (ȇ2)𝜇 = (1/𝑟)𝛿𝜇2, (ȇ3)𝜇 = (1/𝑟sin𝜃)𝛿𝜇2
Schwarzschild 좌표 내의 Riemann tensor의 성분들을 위한 해당 표현들과 더불어서 이 표현들을 (7.28)에 치환해서, 우리는 (7.27)로부터 다음을
만족하는 두 입자들 사이의 직각의 연결하는 vector들의 공간 성분들을 얻는다. (여기의 범위가 이님; 얼마간의 대수 작업 후에)
𝑑2𝜁𝑟̄/𝑑𝜏2 = +(2𝜇𝑐2/𝑟3)𝜁𝑟̄, 𝑑2𝜁𝜃̄/𝑑𝜏2 = -𝜇𝑐2𝜁𝜃̄, 𝑑2𝜁𝜙̄/𝑑𝜏2 = -𝜇𝑐2𝜁𝜙̄.
𝜁𝑟̄ 방정식의 양의 부호는 방사 방향의 한 tension이나 늘어남을 가리키고, 𝜁𝜃̄와 𝜁𝜙̄ 방정식의 음의 부호는 가로지르는 방향의 압축을 기리킨다. 각각의
경우에서 중력의 조석력의 특성인 1/𝑟3 의존성을 주목하라. 더욱이, 조석력은 𝑟 = 2𝜇 에서 어떠한 '변환'이 없으나 𝑟 = 0 에서는 무한하다.
우리는 한 블랙홀 안으로 다리부터 먼저 떨어지는 한 용맹한 우주비행사를 고려해보도록 한다. 위의 유도된 공식들이 정확하게 유효하지 않을 것이다,
왜나하면 그 비행사를 구성하는 입자들(원자들)간에 힘들이 존재할 것이기 때문이다. 그럼에도 불구하고 그 조석력이 강해지면, 우리는 원자간 힘들을
무시할 수 있고, 위에서 유도된 식들이 훌륭한 근사로 유효할 것이다. 그래서 그 조석력은 비행사의 몸을 찢어버릴 뿐만 아니라 그 원자들도 궁극적으로
같은 운명이 될 것이다! 한 인간의 신체를 늘리거나 압축하는 허용 한계는 미터당 ∼400ms2의 한 가속도 구배로 가정하면, 한 인간이 조석력을 견딜 수
있는 Schwarzschild 반경은 다음과 함께하는 어떤 대단히 질량이 큰 블랙홀이다.
𝑀 ≳ 104𝑀⊙.
만일 당신이 한 초대형 블랙홀, 말하자면𝑀 ≳ 109𝑀⊙ (그러한 블랙홀은 여러 은하들의 중심에 있다고 믿어진다.) 을 향해 떨어진다면, 당신은 별 느낌
없이 사건 지평선을 넘어갈 것이다. 하지만, 당신의 운명은 정해져서 - 당신이 탈출할 수 없는 그 특이점을 접근하면서 그 블랙홀의 조석력에 의해 찢겨
져서 끝이 날 것이다. 만일 당신이, 말하지면 질량 10𝑀⊙인 한 '작은' 블랙홀을 향해서 떨어진다면, 당신이 그 사건 지평선에 도달하기도 전에 조석력에
의해서 찢겨질 것이다.
* 2019년 4월 ETH(사건 지평선 망원경) 국제적 연합이 직접 관측한 블랙홀의 모습을 최초로 발표했음.
p.s. 전개 과정이 (지면상 또는 기초적 내용이라) 생략된 수식들을 만나면 답답한데, 여기에는 그런 부분들이 꽤 많음..ㅠ
여기서는 수리물리학적 논리의 상세한 전개보다는 블랙홀에 관련된 물리 현상들의 소개와 그 해설에 더 역점을 두는 듯함.
Faber의 GR과 Dirac의 GR은 입문적/기초적 내용이었지만, 전반적으로 논리 전개가 엄밀해서 좋았읍니다만 ...
|
|
|





































