|
김관석
|
2020-06-07 08:02:59, 조회수 : 669 |
- Download #1 : F15a.jpg (182.6 KB), Download : 1

15. Cosmological models* .
We must continue the previous discussion further. One may use (14.36) (14.39) equations conveniently. Also equation (14.39) can be useful alternative forms as follows
𝑑(𝜌𝑅3)/𝑑𝑡 = - 3𝑝Ṙ𝑅2/𝑐2 , 𝑑(𝜌𝑅3)/𝑑𝑅 = - 3𝑝𝑅2/𝑐2.
And the density and the pressure of a fluid are related by its equation of state. In cosmology we assume that the cosmological fluid follows
𝑝 = 𝑤𝜌𝑐2 or 𝑝𝑖 = 𝑤𝑖𝜌𝑖𝑐2
where the equation-of-state parameter 𝜔 is a constant. Then the energy equation can then be written
𝑑(𝜌𝑅3)/𝑑𝑅 = - 3𝑤𝜌𝑅2.
This equation has the immediate solution, which we can use from now on
(15.0 ← 14.42 & 14.44) 𝜌 ∝ 𝑅-3(1+𝑤) or 𝜌𝑖 ∝ 𝑅-3(1+𝑤𝑖)
15.1 Components of cosmological fluid .
We assume that the cosmological fluid consists of three components, matter, radiation and the vacuum, each with a different equation of state. The total equivalent mass density is simply the sum of each one,
(15.1) 𝜌(𝑡) = 𝜌𝑚(𝑡) + 𝜌𝑟(𝑡) + 𝜌𝛬(𝑡),
where 𝑡 is the cosmic time and we shall assume that these are non-interacting. although matter and radiation did interact in the early universe. So each component has an equation of state of the form
𝑝𝑖 = 𝑤𝑖𝜌𝑖𝑐2,
where the equation-of-state parameter 𝑤𝑖, is a constant and i labels the component. In particular, 𝑤𝑖 = 0 for pressureless 'dust', 𝑤𝑖 = 1/3 for radiation and 𝑤𝑖 = -1 for the vacuum. In general, if 𝑤𝑖 is a constant then, requiring that the weak energy condition is satisfied and that the local sound speed** (𝑑𝑝/𝑑𝜌)1/2 is less than 𝑐, one finds that 𝜔𝑖 must lie in -1 ≤ 𝑤𝑖 ≤ 1. We now discuss each components in turn and conclude with a description of total density as the universe evolve.
[Matter]
In general, matter in the universe may come in several different forms. Indeed, observations of the large-scale structure in the universe suggest the most of he matter is in the form of non-baryonic dark matter, which interact electromagnetically only very weakly and hence invisible or 'dark'. Moreover, dark matter may itself come in different forms, such as cold dark matter (CDM) and hot dark matter (HDM), the naming of which is connected to whether the typical energy of the particle is non-relativistic or relativistic. So we have
𝜌𝑚(𝑡) = 𝜌𝑏(𝑡) + 𝜌𝑑𝑚(𝑡).
But in the following discussion, we will deal only the total matter density that determines how the scale factor 𝑅(𝑡) evolves with cosmic time 𝑡. We shall also commonly assume that the matter particles have thermal energy that is much less than their rest mass energy, and the matter can be considered to be pressureless, i.e. dust. Thus, from (15.0), if a present-day proper density 𝜌𝑚(𝑡o) ≡ 𝜌𝑚,0, its density of some other cosmic time 𝑡 is given by
𝜌𝑚(𝑡) = 𝜌𝑚,0[𝑅o/𝑅(𝑡)]3 or 𝜌𝑚(𝑧) = 𝜌𝑚,0(1 + 𝑧)3,
These expressions concur with our expectation for the behavior of the space density of dust particles in an expanding universe.
[Radiation]
Radiation includes not only photons but also other species with very small or zero rest mass, such as a neutrino, which is a small non-zero rest mass. The total equivalent mass density of radiation in the universe at some cosmic time 𝑡 may be written as follows
𝜌𝑟(𝑡) = 𝜌𝛾(𝑡) + 𝜌𝜈(𝑡).
However, only the total energy density determines the behavior of the scale factor. For radiation, in general, we have 𝑤 = 1/3 and from (15.0), if the total radiation in the universe has a present-day energy density of 𝜌𝑟,0, at other cosmic time,
𝜌𝑟(𝑡) = 𝜌𝑟,0[𝑅o/𝑅(𝑡)]4 or 𝜌𝑟(𝑧) = 𝜌𝑟,0(1 + 𝑧)4,
It is worth nothing that, to a very good approximation, the dominant contribution to the radiation energy density of the universe is due to the photons of the cosmic microwave background (CMB). The radiation is to a very high degree of accuracy uniformly distributed throughout the universe and has a
blackbody form. For blackbody radiation, the number density of photons with frequencies in the range [𝜈, 𝜈 + 𝑑𝜈] is given by,
(15.2) 𝑛(𝜈, 𝑇)𝑑𝜈 = 8π𝜈2/𝑐3(𝑒𝘩𝜈/𝑘𝑇 - 1) 𝑑𝜈,
where 𝑇 is the 'temperature' 0f the radiation. since the energy per unit frequency is simply 𝑢(𝜈, 𝑇) = 𝑛(𝜈, 𝑇)𝘩𝜈, the total equivalent mass density of the radiation is
𝜌𝑟(𝑇) = 1/𝑐2 ∫∞0𝑢𝜈 𝑑𝜈 = 𝑎𝑇4/𝑐2,
where 𝑎 = 4π2𝑘4𝐵/(60ℏ3𝑐3) is the reduced Stefan-Boltzmann constant. observations shows that the CMB is characterized by a present-day temperature 𝑇0 = 2.726𝐾, which corresponds to a total present-day number density 𝑛𝛾,0 ≈ 4 ⨯ 108m-3. It is easily shown that the CMB photon energy distribution retains in general blackbody form as the universe expands. Thus, at any given cosmic time 𝑡, the temperature of the CMB radiation in the universe is given by
(15.3) 𝑇(𝑡) = 𝑇0[𝑅0/𝑅𝑡] or 𝑇(𝑧) = 𝑇0(1 + 𝑧)
[Vacuum]
As the vacuum can be modeled as a perfect fluid having as equation of state 𝑝 = -𝜌𝑐2, so that the fluid has a negative pressure. This corresponds to an equation of state parameter 𝑤 = -1. thus, from (15.0), we see that at any cosmic time 𝑡, we have
𝜌𝛬 = 𝜌𝛬,0 = 𝛬𝑐2/8π𝐺.
[Relative contributions of the components]
On combining the above results, we find
(15.4) 𝜌(𝑡) = 𝜌𝑚,0[𝑅o/𝑅(𝑡)]3 + 𝜌𝑟,0[𝑅o/𝑅(𝑡)]4 + 𝜌𝛬,0.
Typically one wold expect radiation to dominate the total density when 𝑅(𝑡) is small. As the universe expands, the radiation energy density dies away the most quickly and matter becomes the dominent component. Finally, if the universe continues to expand then the matter density also dies away and the vacuum ultimately dominate the energy density. We conclude by that cosmologists often define the normalized scale parameter
𝑎(𝑡) ≡ 𝑅(𝑡)/𝑅o,
in terms of which the above results are more compactly written, since 𝑎o = 1 by definition.
15.2 Cosmological parameters .
In our very simplified model of the universe, its entire history is determined by only a few cosmological parameters. Indeed the three values of the equivalent mass densities , 𝜌𝑚(𝑡), 𝜌𝑟(𝑡) and 𝜌𝛬 and the Hubble parameter 𝐻(𝑡) are sufficient to determine the scale factor 𝑅(𝑡) at all cosmic time using (14.19) (14.36). So the cosmological model is entirely fixed by specifying the four quantity
𝐻0, 𝜌𝑚,0, 𝜌𝑟,0, 𝜌𝛬,0.
However, it is common to work in terms of alternative dimensionless quantities, called density parameters or simply density defined by
(15.5) 𝛺𝑖(𝑡) = 8π𝐺/3𝐻2(𝑡) 𝜌𝑖(𝑡).
In terms of these new dimensionless parameters, the cosmological model may thus be fixed by following the four present-day quantities
(15.6) 𝐻0, 𝛺𝑚,0, 𝛺𝑟,0, 𝛺𝛬,0.
A major goal of obsevational cosmology is therefore to determine these quantities for our universe. With significant advances, about 2005, we know them to an accuracy of a few percent. They are
(15.7) 𝐻0 ≈ 70km s-1Mpc-1) , 𝛺𝑚,0 ≈ 0.3, 𝛺𝑟,0 ≈ 5 , 𝛺𝛬,0 ≈ 0.7,
where 1 Mpc = 10 parsecs ≈ 3.09 ⨯ 1022m; in SI units, 𝐻0 ≈ 2.27 ⨯ 10-18s-1. Perhaps most astonishing is that the present-day energy density of the universe is dominated by the vacuum!
We also note that cosmologists define further these density for the individual contributions to the matter and the radiation. For examples, 𝛺𝑏, 𝛺𝑑𝑚 and 𝛺𝜈 are commonly used to denote the density of baryons, dark matter and nutrinos respectively. For our universe, cosmological observations suggest present-day values
(15.8) 𝛺𝑏,0 ≈ 0.05, 𝛺𝑑𝑚,0 ≈ 0.25, 𝛺𝜈,0 ≈ 0,
where we see the familiar baryonic matter density is one-sixth of the total matter density. Moreover, the majority of the baryonic matter seems not to reside in ordinary (hydrogen-burning) stars; the contribution of such stars is only 𝛺* ≈ 0.008. The values of the individual quantities (15.8) affect the astrophysical process occurring in the universe and have a profound influence on, for example, the formation of the structure.
The reason for defining densities (15.5) becomes clear when we rewrite the second of the cosmological field equations (14.36) in terms of them. Dividing this equation through by 𝑅2 and noting 𝐻 = Ṙ/𝑅, we obtain
(15.9) 1 = 𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 - 𝑐2𝑘/[𝐻2𝑅2],
where, for simplicity, we omitted the explicit time dependence of the variables. It is also common practice to define the curvature density parameter
(15.10) 𝛺𝑘(𝑡) = -𝑐2𝑘/[𝐻2(𝑡) 𝑅2(𝑡)],.
so that all the cosmic times 𝑡, we have the elegant relation
(15.11) 𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 + 𝛺𝑘 = 1.
From (15.9), we see that 𝛺𝑚, 𝛺𝑟 and 𝛺𝛬 determine the spatial curvature in a simple fashion. We have three cases:
𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 < 1 ⇔ negative spatial curvature (𝑘 = -1) ⇔ 'open'
𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 = 1 ⇔ zero spatial curvature (𝑘 = 0) ⇔ 'flat'
𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 > 1 ⇔ positive spatial curvature (𝑘 = 1) ⇔ 'closed'
The fact that the sum of the density parameters is unity means that the universe cannot evolve from one form of the FRW geometry to another. Cosmologists often also define total density parameter
(15.12) 𝛺 ≡ 𝛺𝑚 + 𝛺𝑟 + 𝛺𝛬 = 1 - 𝛺𝑘.
where from (15.1) and (15.50 we see that 𝛺 = 8π𝐺𝜌/(3𝐻2). From the present-day data of (15.7), we also see that for our universe 𝛺0 ≈ 1 or equivalently 𝛺𝑘,0 ≈ 0, and it is therefore close to being spatially flat (𝑘 = 0).
Finally, for flat cosmological model one require 𝛺 = 1 and it is common to describe the corresponding total equivalent mass density as the critical density and the value of present-day critical density are
(15.12a) 𝜌crit ≡ 3𝐻2/8π𝐺. 𝜌crit,0 ≈ 9.2 ⨯ 10-27 kg m-3.
Also it is worth noting that 𝜌crit,0 ≈ 5.5 protons m-3 which is extremely low by laboratory standards.
15.3 The cosmological field equations .
Recalling that 𝐻 = Ṙ/𝑅, the second cosmological field equations of (14.36) may be written
𝐻2 = 8π𝐺/3(𝛴𝑖𝜌i) - 𝑐2𝑘/𝑅2,
where the label 𝑖 includes matter, radiation and the vacuum. From (15.4), (15.5) and (15.10), we therefore find
(15.13) 𝐻2 = 𝐻02(𝛺𝑚,0 𝑎-3 + 𝛺𝑟,0 𝑎-4 + 𝛺𝛬 + 𝛺𝑘,0 𝑎-2).
where 𝑎 = 𝑅/𝑅0. Since 𝑎 = 𝑅/𝑅0 = (1 + 𝑧)-1, the equation (15.13) may yield an expression of the Hubble parameter 𝐻(𝑧) as a function of redshift 𝑧.
We now turn to the first equation in (14.36). multiplying the equation through by 𝑅/Ṙ2 and using equation-of- state parameter 𝑤 = 𝑝/𝜌𝑐2, we have
𝑅Ȑ/Ṙ2 = - 4π𝐺/(3𝐻2) 𝛴𝑖𝜌𝑖(1 + 𝑤𝑖),
where left-hand side is equal to minus the deaccecleration parameter 𝑞 defined in (14.19) as 𝑞(𝑡) ≡ -𝑅(𝑡)Ȑ(𝑡)/Ṙ(𝑡)2. Thus using (15.5) and substituting 𝑤i, one finds the neat relation
(15.14) 𝑞 = 1/2 (𝛺𝑚 + 2𝛺𝑟 - 2𝛺𝛬).
Also one can write this equation in terms of present-day values by using the result (15.13)
𝛺𝑖 = 𝛺𝑖,0(𝐻0/𝐻)2 𝑎-3(1 + 𝑤𝑖).
15.4 General dynamical behavior of the universe .
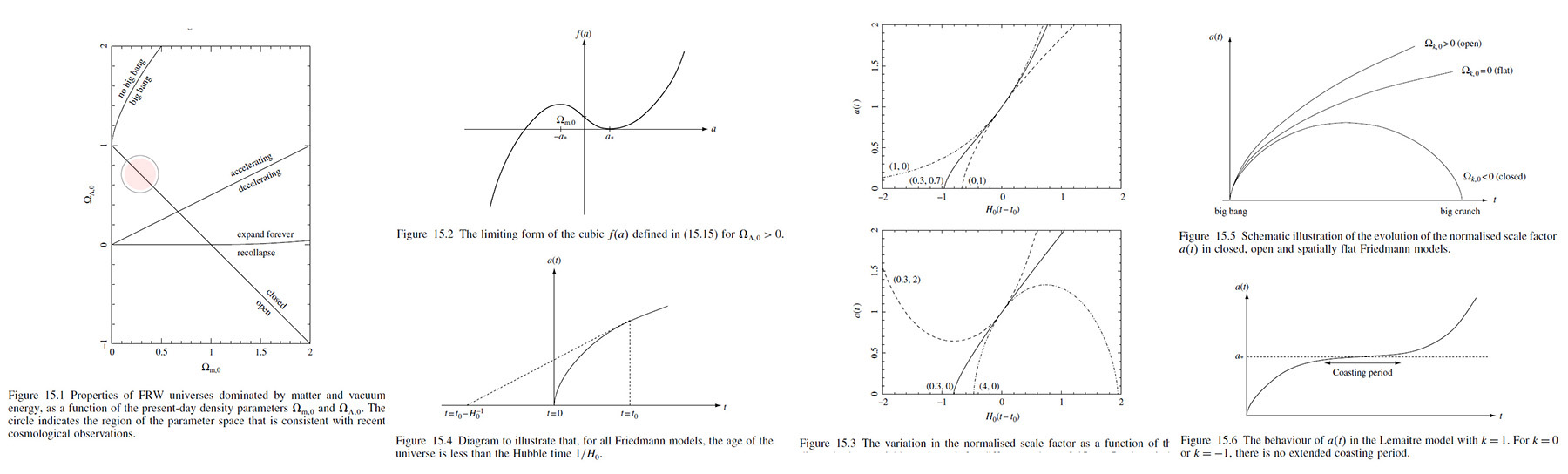
Because 𝛺𝑟,0 is significantly smaller than 𝛺𝑚,0 or 𝛺𝛬,0 according to the observations (15.7), it is a reasonable approximation to neglect it and parameterize a universe in terms of just 𝛺𝑚,0 and 𝛺𝛬,0. Figure 15.1 is a marvelous summary of the properties of FRW universe dominated by matter and vacuum energy (known as Lemaitre models). In the figure the 'open-close' line comes from (15.11) in case of zero spatial curvature
𝛺𝛬,0 = 1 - 𝛺𝑚,0.
The 'accelerating-decelerating' line is obtained by setting 𝑞0 = 0 in (15.14) for 𝑡 = 𝑡0, which gives
𝛺𝛬,0 = 1/2 𝛺𝑚,0.
When we set 𝑡 = 𝑡* for 𝐻(𝑡*) = 0 in (15.13), we can rearrange as follows
(15.15) 𝑓(𝑎) ≡ 𝛺𝛬,0𝑎3 + (1 - 𝛺𝑚,0 - 𝛺𝛬,0)𝑎 + 𝛺𝑚,0 = 0.
In the figure for the case 𝛺𝛬,0 < 0 from (15.14) we may deduced that Ȑ or a is always negative and Ṙ > 0 (because we observe redshifts), hence the 𝑎(𝑡) graph must be convex for all values of 𝑡. This means that 𝑎(𝑡) must have equaled zero at some point in the past, usually in 𝑡 = 0 and the universe must eventually recollapse. As the universe expands, the vacuum energy eventually dominates and and so we need only consider the 𝛺𝛬 on the right-hand side of (15.14), which will not tend to zero as the scale factor increases. Thus a cannot tend to zero and so 𝑎 → 0 at some finite cosmic time in the future.
In case of 𝛺𝛬,0 = 0, the equation (15.15) has the single solution 𝑎* = 𝛺𝑚,0/(𝛺𝑚,0 - 1), which is negative in the range 0 ≤ 𝛺𝑚,0 ≤ 1, indicating that there is no turning point. Therefore over this range, the 'expand-forever-recollapse' line is simply given by 𝛺𝛬,0 = 0.
Finally in case of 𝛺𝛬,0 > 0, 𝑓(𝑎) → ∓∞ as 𝑎 → ∓∞ and 𝑓(0) = 𝛺𝑚,0 ≈ 0.3. Thus 𝑓(𝑎) has a positive root, it must have a turning point in the region 𝑎 > 0. On evaluating the derivatives 𝑓'(𝑎) and 𝑓"(𝑎) with respect to 𝑎, 𝑓(𝑎) must have the general form illustrated in Figure 15.2. Thus we requires 𝑓(𝑎*) = 𝑓'(𝑎) = 0, which yields
(15.16) 𝑎* = (𝛺𝑚,0/2𝛺𝛬,0)1/3.
On substituting this expression back into (15.5) one can a equations for 𝛺𝛬,0 > 0, given by
(15.17) 4(1 - 𝛺𝑚,0 - 𝛺𝛬,0)3 + 27𝛺𝑚,02𝛺𝛬,0 = 0
By introducing the variable 𝑥 = [𝛺𝛬,0/4𝛺𝑚,0)]1/3, we have
𝑥3 - 3𝑥/4 + (𝛺𝑚,0 - 1)/4𝛺𝑚,0 = 0,
Which is convenient form to finding the solutions. If we write in terms of 𝛺𝛬,0, one finds the following three cases:
• 0 < 𝛺𝑚,0 ≤ 1/2, one positive root at
(15.18) 𝛺𝛬,0 = 4𝛺𝑚,0 cosh3[1/3 cosh-1 (1 - 𝛺𝑚,0)/𝛺𝑚,0];
• 0 < 𝛺𝑚,0 ≤ 1/2, one positive root at
(15.19) 𝛺𝛬,0 = 4𝛺𝑚,0 cosh3[1/3 cos-1 (1 - 𝛺𝑚,0)/𝛺𝑚,0];
• 𝛺𝑚,0 > 1, two positive root, larger given by (15.19) and smaller by
(15.20) 𝛺𝛬,0 = 4𝛺𝑚,0 cos3[1/3 cosh-1 (1 - 𝛺𝑚,0)/𝛺𝑚,0].
Moreover, from (15.16), we finds that 𝑎* < 1 for (15.18, 15.19), whereas 𝑎* > 1 for (15.20). the universe is expanding, if 𝑎* < 1, there is a turning pint in the past and no big bang, whereas 𝑎* > 1, there is a turning point in the future (i.e. recollapse).
The resulting lines of Figure 15.1 shows some interesting features. In particular, when 𝛺𝛬,0 = 0, any combination of spatial geometry and eventual fate is possible. It is worth noting that the red colored region is consistent with the recent cosmological observations of (0.3, 0.7) in 𝑘 = 0, i.e. flat spatial model, These shows that the expansion of the universe to be accelerating and during 1998 the accelerating expansion was astonishingly discovered! They also require the universe to have started at a big bang at some finite cosmic time in the past and to expand forever in the future.
15.5 Evolution of the scale factor .
We now discusshow to find the form of the 𝑎(𝑡) curve at all cosmic times, for a given st of present-day cosmological parameters. From (15.13), remembering 𝐻 = ά/𝑎 and multiplying 𝑎2, we obtain
(15.21) (𝑑𝑎/𝑑𝑡)2 = 𝐻02(𝛺𝑚,0 𝑎-1 + 𝛺𝑟,0 𝑎-2 + 𝛺𝛬 𝑎2 + 1 - 𝛺𝑚,0 - 𝛺𝑟,0 - 𝛺𝛬,0).
It is more convenient to introduce the new dimensionless variable
(15.22) 𝙩 = 𝐻0(𝑡 - 𝑡0),
which measures cosmic time relative to the present epoch in the units of the 'Hubble time' 𝐻0-1. in terms of 𝙩, (15.21) becomes
(15.23) (𝑑𝑎/𝑑𝙩)2 = 𝛺𝑚,0 𝑎-1 + 𝛺𝑟,0 𝑎-2 + 𝛺𝛬 𝑎2 + 1 - 𝛺𝑚,0 - 𝛺𝑟,0 - 𝛺𝛬,0.
When 𝙩 = 0 (the present epoch) , for which 𝑎0 = 1, the normalized scale factor at time step 𝑛 + 1 can be approximated by Taylor expansion
(15.24) 𝑎𝑛 + 1 ≈ 𝑎𝑛 + (𝑑𝑎/𝑑𝙩)𝑛 𝛥𝙩 + 1/2 (𝑑2𝑎/𝑑𝙩2)𝑛 (𝛥𝙩)2,
where 𝛥𝙩 is the small step size. The coefficient of 𝛥𝙩 and (𝛥𝙩)2 are given by (15.23) directly and differentiating it.
Figure 15.3 shows the variation in the normalized scale factor 𝑎(𝙩) for different values of (𝛺𝑚,0, 𝛺𝛬,0). In the top panel see that the solid line corresponds to the case (0.3, 0.7) and the present epoch 𝙩 = 0 corresponds closely to the point of inflection on the curve 'coincidentally'. A second such 'coincident' is that the age of the universe in this model is very close to one Hubble time 𝐻0-1.*** The broken-and-dotted line in the panel of the case (0, 1) is known as de Sitter model, which will be discussed later, has no big-bang origin and will expand forever. The other one the case (1, 0) is known as Einstein-de-Sitter model does have a big-bang origin and is on the borderline between expanding forever and recollapsing; it will in fact expand forever but ά → 0, as 𝙩 → ∞.
In the bottom panel we have 𝛺𝑚,0 + 𝛺𝛬,0 ≠ 1 and so the universe is spatially curved; in the case (0.3, 0) is open and the case (0.3, 2) and (4, 0) are closed. We see that the former has no big-bang origin and known as a bounce model, and the latter corresponds to a cosmological model with a big-bang origin that expands to some finite minimum value of a before recollapsing to a big crunch.
It is worth to discuss the general case in the limit 𝑎 → 0. We can assume that the energy density of the universe is dominated by one kind of source. in this case, (15.23) can be written
(15.25) (𝑑𝑎/𝑑𝙩)2 = 𝛺𝑖,0 𝑎-(1+3𝑤𝑖) + 𝛺𝑘,0,
where the label 𝑖 denotes the dominant form of the energy density as 𝑎 → 0 and 𝑤𝑖 th corresponding equation-of-state parameter. Moreover, if we restrict our attention to the realistic case, in which 𝑖 denote ether dust (𝑤𝑖 = 0) or radiation (𝑤𝑖 = 1/3) and neglect the curvature density 𝛺𝑘,0. So we integrate (15.25) and obtain
(15.26) 𝑎(𝙩) = ∓[3/2 (1+𝑤𝑖)√𝛺𝑖,0]2/[3(1+𝑤𝑖)] (𝙩 - 𝙩*)2/[3(1+𝑤𝑖)],
where 𝙩* is the value of 𝙩 at which 𝑎 = 0 and the plus and minus sign correspond to the big bang and big crunch respectively. From (15.25) we also note that 𝑑𝑎/𝑑𝙩 → ∞ as `𝑎 → 0. Thus we conclude that the 𝑎(𝙩)-graphs meets the 𝙩-axis at right angles.
15.6 Analytical cosmological models .
Although in the general case the evolution of the (normalized) scale factor 𝑎(𝑡) must be solved explicitly, there exist a number of special cases, corresponding to the particular values of cosmological parameters 𝛺𝑚,0, 𝛺𝑟,0 and 𝛺𝛬,0, for which equation (15. 21) can be solved analytically. We now discuss some of these analytical models in terms of cosmic time 𝑡 directly.
[The Friedmann models]
Cosmological models with a zero cosmological constant is known as the Friedmann models, after the mathematician A. A. Friedmann (1888-1925). Figure 15.4 shows some information without solving the equations (14.36) and (15.21) explicitly. We see that the 𝑎(𝑡)-curve is everywhere convex and it crosses the point (𝑡0, 𝑎0) (note that 𝑎0 = 1) and the tangent of the point reaches the 𝑡-axis if the expansion had been uniform, that is, ά = constant and ἄ = 0. The time elapsed from that point to the present epoch is simply ά(𝑡0)/𝑎(𝑡0) = 𝐻0-1 i.e. the Hubble time. Thus
𝑡0 < 𝐻0-1.
After the big-bang, the evolution depends critically on the curvature density parameter 𝛺𝑘,0 = 1 - 𝛺𝑚,0 - 𝛺𝑟,0. From (15.21) we can distinguish three possible histories depending on 𝛺𝑘,0:
𝛺𝑘,0 > 1 ⇔ open (𝑘 = -1) ⇔ ά → non-zero constant as 𝑎 → ∞,
𝛺𝑘,0 = 0 ⇔ flat (𝑘 = 0) ⇔ ά → 0 as 𝑎 → ∞,
𝛺𝑘,0 < 1 ⇔ closed (𝑘 = 1) ⇔ ά = 0 at some finite value 𝑎max.
The three case above are illustrated in Figure 15.5. We shall now find explicit analytical solutions in some special cases.
Dust-only Friedmann models (𝛺𝛬,0 = 0, 𝛺𝑟,0 = 0) In this case (15.21) becomes as follows and also one may obtains expressions for 𝜌𝑚(𝑡) = 𝜌𝑚,0𝑎-3 and 𝛺𝑚(𝑡),
(15.27) ά2 = 𝐻02(𝛺𝑚,0𝑎-1 + 1 - 𝛺𝑚,0) ⇒ 𝑡 = 1/𝐻0 ∫0𝑎[𝑥/{𝛺𝑚,0 + (1 - 𝛺𝑚,0)𝑥}]1/2 𝑑𝑥
• For 𝛺𝑚,0 = 1 (𝑘 = 0), known as the Einstein-de-Sitter (or EdS) model,
(15.28a) 𝑎(𝑡) = (3/2 𝐻0𝑡)2/3
• For 𝛺𝑚,0 > 1 (𝑘 = 0), the integral (15.27) can be evaluated by substituting 𝑥 = [𝛺𝑚,0/(𝛺𝑚,0 -1)] sin2(𝜓/2), where 𝜓 is known as the development angle between [0, π]. One then obtains a cycloid graph,
(15.28b) 𝑎 = 𝛺𝑚,0/2(𝛺𝑚,0 -1) (cos 𝜓 - 1), 𝑡 = 𝛺𝑚,0/2𝐻0(𝛺𝑚,0 -1)3/2 (𝜓 - sin 𝜓),
• For 𝛺𝑚,0 < 1 (𝑘 = -1), the integral (15.27) can be evaluated by substituting 𝑥 = [𝛺𝑚,0/(1 - 𝛺𝑚,0)] sinh2(𝜓/2), and on obtains
(15.28c) 𝑎 = 𝛺𝑚,0/2(1 - 𝛺𝑚,0) (cosh 𝜓 - 1), 𝑡 = 𝛺𝑚,0/2𝐻0(1 - 𝛺𝑚,0)3/2 (sinh 𝜓 - 𝜓),
Rdiation-only Friedmann models (𝛺𝛬,0 = 0, 𝛺𝑚,0 = 0) In this case (15.21) becomes as follows and also one may obtains expressions for 𝜌𝑟(𝑡) = 𝜌𝑟,0𝑎-4 and 𝐻(𝑡) = ά/𝑎 and hence for 𝛺𝑟(𝑡),
(15.29a) ά2 = 𝐻02(𝛺𝑟,0𝑎-2 + 1 - 𝛺𝑟,0) ⇒ 𝑡 = 1/𝐻0 ∫0𝑎[𝑥/√{𝛺𝑟,0 + (1 - 𝛺𝑟,0)𝑥2} 𝑑𝑥,
• For 𝛺𝑟,0 = 1 (𝑘 = 0), we find that
(15.29b) 𝑎(𝑡) = (2𝐻0𝑡)1/2.
• For 𝛺𝑟,0 < 1 (𝑘 = -1) and 𝛺𝑟,0 > 1 (𝑘 = 1), the integral (15.27) can be evaluated by inspection give
(15.29c) 𝑎(𝑡) = (2𝐻0𝛺𝑟,01/2𝑡)1/2[1 + (1 - 𝛺𝑟,0)/2𝛺𝑟,01/2 𝐻0𝑡]1/2.
spatially flat Friedmann models (𝛺𝛬,0 = 0, 𝛺𝑚,0 + 𝛺𝑟,0 = 1) In this case (15.21) becomes
(15.30a) ά2 = 𝐻02(𝛺𝑚,0𝑎-1 + 𝛺𝑟,0𝑎-2) ⇒ 𝑡 = 1/𝐻0 ∫0𝑎 𝑥/√(𝛺𝑚,0𝑥 + 𝛺𝑟,0) 𝑑𝑥,
which may be integrating by substituting 𝑦 = 𝛺𝑚,0𝑥 + 𝛺𝑟,0
(15.30b) 𝐻0𝑡 = 2/3𝛺𝑚,02 [(𝛺𝑚,0𝑎 + 𝛺𝑟,0)1/2(𝛺𝑚,0𝑎 - 2𝛺𝑟,0) + 2𝛺𝑟,03/2].
Thogh this expression cannot be easily inverted to give 𝑎(𝑡), it becomes 2/3 𝑎3/2 for a matter-only model and 1/2 𝑎2 for a radiation-only model, and therefore agrees with our earlier results.
[The Lemaitre models]
The Lemaitre models are a generalization of the Friedmann models in which the cosmological constant is non-zero. In particular we will focus on matter-only models .
Matter-only Lemaitre models with arbitrary spatial curvature (𝛺𝑟,0 = 0) In this case (15.13) reads
(15.31) ά2 = 𝐻02(𝛺𝑚,0𝑎-1 + 𝛺𝛬,0𝑎2 + 𝛺𝑘,0) = 𝐻02(𝛺𝑚,0𝑎-1 + 𝛺𝛬,0𝑎2 + 1 - 𝛺𝑚,0 - 𝛺𝛬,0),
Though the equation is very complicate to solve for 𝑎(𝑡), we see that for small 𝑎 the first term on the right-hand side dominates and for large 𝑎 the second term does. Thus, the 𝑎(𝑡)-curve at first increases as, after starting from a big-bang origin at 𝑡 = 0, then the matter energy density decreases and the vacuum energy eventually dominates.
𝑎(𝑡) = (3/2 𝐻0 √𝛺𝑚,0 𝑡)2/3 (for small 𝑡);
𝑎(𝑡) ∝ exp (𝐻0 √𝛺𝛬,0 𝑡) (for large 𝑡).
From the above behavior the universe must make a transition from a decelerating to an accelerating phase. This occurs when ἄ = 0 where has a point of inflection. Differentiating (15.31), we find that
(15.32) ἄ = 1/2 𝐻02(2𝛺𝛬,0𝑎 - 𝛺𝑚,0𝑎-2𝑎-2).
From this result, we may verify that when 𝑎 is small, we have ἄ < 0 and so the expansion is decelerating and the deceleration gradually decrease until ἄ changes sign, after which the expansion accelerates ever more rapidly. We see that ἄ = 0 occurs is given by
(15.33) 𝑎* = (𝛺𝑚,0/2𝛺𝛬,0)1/3.
To obtain an approximate analytical expression for 𝑎(𝑡) in the vicinity of the point of inflection, denoting the cosmic time of inflection by 𝑡*, we may perform separate Taylor expansion of 𝑎 and ά2 about 𝑡 = 𝑡* when ἄ = 0 with the notation of 𝑎* ≡ 𝑎(𝑡*),
𝑎 ≈ 𝑎* + ά*(𝑡 - 𝑡*) and ά2 ≈ ά*2 + ά* 𝑑3𝑎*/𝑑𝑡*3 (𝑡 - 𝑡*)2,
(15.34) ά2 ≈ ά*2 + [𝑑3𝑎*/𝑑𝑡*3 (𝑎 - 𝑎*)2]/ά*2.
Differentiating (15.32) to obtain the third derivative of 𝑎(𝑡), 𝑑3𝑎/𝑑𝑡3 and using (15.33) and (15.31) in turn, one finds that (15.34) becomes
ά2 ≈ 𝐻02[𝛺𝑘,0 + 3𝛺𝛬,0𝑎*2 + 𝛺𝛬,0(𝑎 - 𝑎*)2].
This equation can now integrated analytically and has the solution
(15.35) 𝑎(𝑡) = 𝑎* + 𝑎*[1 + 1/3 𝛺𝑘,0(1/4 𝛺𝛬,0𝛺𝑚,02)-1/3 ]1/2 sinh [𝐻0(3𝛺𝛬,0)1/2 (𝑡 - 𝑡*)]
An interesting property of the model is that in case of 𝑘 = 1, there is a 'coasting period' in the vicinity where ἄ = 0 during which the value of 𝑎(𝑡) remains almost equals to 𝑎* (see Figure 1.6)). In (15.35) by setting 1/3 𝛺𝑘,0(1/4 𝛺𝛬,0𝛺𝑚,02)-1/3 sufficiently close to -1.
Spatially flat matter-only Lemaitre models (𝛺𝑟,0 = 0, 𝛺𝑚,0 + 𝛺𝛬,0 = 1) In this case one can give an explicit formula for the scale factor. So the cosmological field equation (15.13) may be written
ά2 = 𝐻02[(1 - 𝛺𝛬,0)𝑎-1 + 𝛺𝛬,0𝑎2] ⇒ 𝑡 = 1/𝐻0 ∫0𝑎 𝑥/√{(1 - 𝛺𝛬,0)𝑥 + 𝛺𝛬,0)𝑥4} 𝑑𝑥.
This integral can be made tractable by the substitution 𝑦2 = 𝑥3∣𝛺𝛬,0∣/(1 - 𝛺𝛬,0), which yields
𝐻0𝑡 = 2/(3√∣𝛺𝛬,0∣) ∫0√{𝑎3∣𝛺𝛬,0∣/(1 - 𝛺𝛬,0)} 𝑑𝑦/√(1 ∓ 𝑦2),
where the plus sign corresponds to the case 𝛺𝛬,0 > 0 and the minus sign to 𝛺𝛬,0 < 0. This may now intergrated to give
(15.36) 𝐻0𝑡 = 2/(3√∣𝛺𝛬,0∣) sinh-1 [√{𝑎3∣𝛺𝛬,0∣/(1 - 𝛺𝛬,0)}] if 𝛺𝛬,0 > 0.
𝐻0𝑡 = 2/(3√∣𝛺𝛬,0∣) sin-1 [√{𝑎3∣𝛺𝛬,0∣/(1 - 𝛺𝛬,0)}] if 𝛺𝛬,0 < 0.
From (15.36) we may obtain analytic expressions for 𝐻(𝑡), 𝜌𝑚(𝑡), 𝛺𝑚(𝑡) and 𝛺𝛬(𝑡).
[The de Sitter model]
The de Sitter model is a particular special case of a Lemaitre model defined by the cosmological parameters 𝛺𝑚,0 = 0, 𝛺𝑟,0 = 0 and 𝛺𝛬,0 = 1. This model is therefore spatially flat and has some close connection with the theory of inflation (see Section 16.1).
For the de Sitter model, the cosmological field equation (15.13) reads
(ά/𝑎)2 = 𝐻02.
which tells us that the Hubble parameter 𝐻(𝑡) is a constant the normalized scale factor increase exponentially as
𝑎(𝑡) = exp[𝐻0(𝑡 - 𝑡0) = exp[√(𝛬/3) 𝑐(𝑡 - 𝑡0),
where the second equality is expressed in terms of the cosmological constant 𝛬. Thus, the de Sitter model has no big-bang singularity at a finite time in the past.
[Einstein's static universe]
Einstein derive his field equations well before the discovery of the expansion of the universe and he was worried that he could not find static cosmological solutions. He therefore introduced the cosmological constant to constructing static solution.
For 𝛬 > 0 and static universe, i.e. ἄ = ά = 0, the Hubble parameter 𝐻 is zero always, and from (14.36) we see that we require
4π𝐺𝜌𝑚,0 = 𝛬𝑐2 = 𝑐2𝑘/𝑅02.
In fact the first equality can be succinctly written as 𝜌𝑚,0 = 2𝜌𝛬,0. Since 𝛬 is positive we thus require 𝑘 = 1, so the universe has positive spatial curvature.
How well did Einstein's static universe fit with cosmological observations of the time? For the mean matter density, recent cosmological observations suggest that
𝜌𝑚,0 ≈ 3 ⨯ 10-27kgm-3.
Adopting the above value of 𝜌𝑚,0, we find that the scale factor is 𝑅0 ≈ 2 ⨯ 1026m ≈ 6000 MPc which is more than sufficient for the closed spacial geometry to encompass the observable universe. Also 𝛬 = 1/𝑅02 = 2.5 ⨯ 10-53m-2 which is small enough to evade the limits on 𝛬 from Solar system experiments. (∣𝛬∣ ≤ 10-45m-20.
However, it has the theoretically undesirable feature of being unstable. Since the cosmological constant must be fine-tuned to match the density of the universe, thus if we add or subtract one proton from the universe or convert some matter into radiation, the balance between gravity and the cosmological constant will be disturbed and the universe will begin to expand or contract.
.
* Textbook: M.P. Hobson, G. Efstathiou and A.N. Lasenby General Relativity An Introduction for Physicists (Cambridge University Press 2006)
** local sound speed: ?
*** Whether such coincidences have some deeper significance is the the subject of current cosmological research.
※ attention: some rigorous derivation might be required |
|
|





































