|
김관석
|
2020-09-17 21:43:31, 조회수 : 2,752 |
- Download #1 : as_Schroed7.jpg (249.7 KB), Download : 9

The Schrödinger Equation (1) (2) (3) (4) (5) (6)
5.3 Harmonic Oscillator
The quantum harmonic oscillator is worth our attention for several reasons. One of those reasons is that it provides an instructive example of the application of several of concepts of previous sections and chapters. The potential-energy function 𝑉(𝑥) of harmonic oscillator is a reasonable approximation for other potential energy functions in the vicinity of a potential minimum. This means that the harmonic oscillator, although idealized in this treatment, has a strong connection to several real-world configurations.
We may review the basics of the behavior of a system such as a mass sliding on a frictionless horizontal surface while attached to a spring. In the classical case, this type of system oscillates with constant total energy, continuously exchanging potential and kinetic energy as it moves from the equilibrium position to the "turning points" at which its direction of motion reverses. The potential energy of that object is zero at the equilibrium position and maximum at the turning points at which the spring is maximally compressed or extended. Conversely the kinetic energy is maximum as the object passes through equilibrium and zero when object's velocity passes through zero at the turning points. The object moves fastest at equilibrium and slowest at the turning points, which means that measurements of position taken at random times are more likely to yield results near the turning points, because the object spends more time there.
Several aspects of classical harmonic oscillator are relevant to the quantum case.
One of them is the quadratic form of potential energy, usually written as
(5.56) 𝑉(𝑥) = 1/2 𝑘𝑥2,
where 𝑥 represents the distance of the object from the equilibrium position and 𝑘 represents the "spring constant" (the force on the object per unit distance from the equilibrium position). The quadratic relationship between potential energy and position pertain to any restoring force that increases linearly with distance, that is, any force that obeys Hook's Law:
(5.57) 𝐹 = -𝑘𝑥,
where the minus sign indicates that the force is always in the direction toward the equilibrium point. We can see the relationship between Hooke's Law and quadratic potential energy by writing force as the negative gradient of the potential energy:
(5.58) 𝐹 = -∂𝑉/∂𝑥 = -∂(1/2 𝑘𝑥)/∂𝑥 = -2𝑘𝑥/2 = -𝑘𝑥,
Another useful result from classical harmonic oscillator is that the motion of the object is sinusoidal, with angular frequency 𝜔 give by
(5.59) 𝜔 = √(𝑘/𝑚),
where 𝑘 represents the spring constant and 𝑚 represents the mass of the object.
We can see a plot of the potential energy of a harmonic oscillator in Fig. 5.25. As in the potential wells we can find the energy levels and wavefunctions of the quantum harmonic oscillator by using separation of variables and solving the TISE (Eq. 3.40). So we have
(5.60) -(ℏ2/2𝑚) 𝑑2𝜓(𝑥)/𝑑𝑥2 + 1/2 𝑘𝑥2𝜓(𝑥) = 𝐸𝜓(𝑥).
It's customary to use angular frequency 𝜔 rather than spring constant 𝑘 in quantum mechanics. Plugging 𝑘 = 𝑚𝜔2 into the TISE gives
𝑑2𝜓(𝑥)/𝑑𝑥2 - 2𝑚/ℏ2[1/2 𝑚𝜔2𝑥2𝜓(𝑥)] = - 2𝑚/ℏ2𝐸𝜓(𝑥) 𝑑2𝜓(𝑥)/𝑑𝑥2 - [(𝑚2𝜔2/ℏ2)𝑥2𝜓(𝑥)] + (2𝑚/ℏ2)𝐸𝜓(𝑥) = 0
(5.61) 𝑑2𝜓(𝑥)/𝑑𝑥2 + [(2𝑚/ℏ2)𝐸 - (𝑚2𝜔2/ℏ2)𝑥2]𝜓(𝑥) = 0.
There are two different approaches to solve it, called the "analytic" approach and the "algebraic" approach. The former uses power series to solve Eq. 5.61 and the latter approach involves factoring the equation and an operator called a "ladder operator. Before starting the analytic path, we make two variable substitutions, which is to replace a dimensional variables, such as 𝐸 and 𝑥, with a dimensionless quantity, such as 𝐸𝑟𝑒𝑓 and 𝑥𝑟𝑒𝑓. The dimensionless version of energy is called 𝜖. defined like this:
(5.62) 𝜖 ≡ 𝐸/𝐸𝑟𝑒𝑓 = 𝐸/(1/2 ℏ𝜔),
where 𝜔 is the angular frequency of the ground-state wavefunction, and ℏ𝜔/2 turns out to be the ground-state energy of the quantum harmonic oscillator.
The dimensionless version of position is called 𝜉, defined by
(5.63) 𝜉 ≡ 𝑥/𝑥𝑟𝑒𝑓 = 𝑥/√(ℏ/𝑚𝜔),
where √(ℏ/𝑚𝜔) represent is the distance to the classical turning point of a harmonic oscillator for a particle in the ground state. Both 𝐸𝑟𝑒𝑓 and 𝑥𝑟𝑒𝑓 are shown in Fig. 5.25.
Now we may start by solving Wqs. 5.62 and 5.63 for 𝐸 and 𝑥, respectively:
(5.64, 65) 𝐸 = 𝜖𝐸𝑟𝑒𝑓 = 𝜖(1/2 ℏ𝜔), 𝑥 = 𝜉𝑥𝑟𝑒𝑓 = 𝜉√(ℏ/𝑚𝜔)
Next, it's necessary to work on the second-order spatial derivative 𝑑2/𝑑𝑥2. Taking the first spatial derivative of 𝑥 with respect to 𝜉 gives
(5.66) 𝑑𝑥/𝑑𝜉 = √(ℏ/𝑚𝜔), 𝑑𝑥 = √(ℏ/𝑚𝜔) 𝑑𝜉, and so
(5.67) 𝑑𝑥2 = ℏ/𝑚𝜔 𝑑𝜉2.
Plugging in the these expressions for 𝐸, 𝑥, and 𝑑𝑥2 into Eq. 5.61, which gives
𝑑2𝜓(𝜉)/(ℏ/𝑚𝜔 𝑑𝜉2) + [(2𝑚/ℏ2)𝜖(1/2 ℏ𝜔) - (𝑚2𝜔2/ℏ2){𝜉√(ℏ/𝑚𝜔)}2]𝜓(𝜉) = 0, 𝑚𝜔/ℏ 𝑑2𝜓(𝜉)/𝑑𝜉2 + (𝑚𝜔/ℏ 𝜖 - 𝑚𝜔/ℏ 𝜉2)𝜓(𝜉) = 0
(5.68) 𝑑2𝜓(𝜉)/𝑑𝜉2 + (𝜖 - 𝜉2)𝜓(𝜉) = 0.
Differential equation of this type called Weber equations, for which the solutions are known be the products of Gaussian function and Hermite polynomials . Because 𝑑2𝜓/𝑑𝑥2 represents the curvature of the wavefunction 𝜓 over distance, 𝜖 is proportional to 𝐸, and 𝜉2 is proportional to 𝑥2, Eq. 5.68 means that the magnitude of the curvature of harmonic oscillator wavefunctions increases as energy increases, but for a given energy, the wavefunction curvature decreases with distance from the center of the potential well.※
If we consider the asymptotic behavior of the solution 𝜓(𝜉) (that is, the behavior at very large or very small values of 𝜉), we can separate out the behavior of the solution in one regime frm that in another, and the differential equation may be simpler to solve in those regimes. For large 𝜉, the Eq. 5.68 looks like this:
(5.69) 𝑑2𝜓(𝜉)/𝑑𝜉2 - 𝜉2)𝜓(𝜉) ≈ 0 𝑑2𝜓(𝜉)/𝑑𝜉2 ≈ 𝜉2)𝜓(𝜉),
where the 𝜖 term is negligible relative to the 𝜉2 term for large 𝜉.
The solutions in this equation for large 𝜉 are ※
(5.70) 𝜓(𝜉 → ∓∞) = 𝐴𝑒𝜉2/2 + 𝐵𝑒-𝜉2/2,
but for the harmonic oscillator, if 𝜉 → ∓∞ the, then the potential energy 𝑉(𝑥) increases infinitely and wavefunction 𝜓(𝜉) must go zero. So the coefficient 𝐴 must be zero and we can write
(5.71) 𝜓(𝜉) = 𝑓(𝜉)𝑒-𝜉2/2,
where the 𝑓(𝜉) represents a function that determines the behavior of 𝜓(𝜉) at small values of 𝜉, and the coefficient 𝐵 has been absorbed into the function. Plugging Eq. 5.71 into Eq. 5.68:
(5.72) 𝑑2[𝑓(𝜉)𝑒-𝜉2/2]/𝑑𝜉2 + (𝜖 - 𝜉2)𝑓(𝜉)𝑒-𝜉2/2 = 0.
The first spatial dervative:
𝑑[𝑓(𝜉)𝑒-𝜉2/2]/𝑑𝜉 = 𝑑𝑓(𝜉)/𝑑𝜉 𝑒-𝜉2/2 + 𝑓(𝜉) 𝑑(𝑒-𝜉2/2)/𝑑𝜉 = 𝑑𝑓(𝜉)/𝑑𝜉 𝑒-𝜉2/2 + 𝑓(𝜉) (-𝜉𝑒-𝜉2/2) = 𝑒-𝜉2/2[𝑑𝑓(𝜉)/𝑑𝜉 - 𝜉𝑓(𝜉)],
and taking another spatial derivative gives
𝑑/2[𝑓(𝜉)𝑒-𝜉2/2]/𝑑𝜉/2 = 𝑑{𝑒-𝜉2/2[𝑑𝑓(𝜉)/𝑑𝜉 - 𝜉𝑓(𝜉)]}/𝑑𝜉 = 𝑑(𝑒-𝜉2/2)/𝑑𝜉 [𝑑𝑓(𝜉)/𝑑𝜉 - 𝜉𝑓(𝜉)] + 𝑒-𝜉2/2 𝑑/𝑑𝜉 [𝑑𝑓(𝜉)/𝑑𝜉 - 𝜉𝑓(𝜉)]
= -𝜉𝑒-𝜉2/2 𝑑𝑓(𝜉)/𝑑𝜉 - 𝜉𝑒-𝜉2/2[- 𝜉𝑓(𝜉)] + 𝑒-𝜉2/2 𝑑2𝑓(𝜉)/𝑑𝜉2 + 𝑒-𝜉2/2[-𝑓(𝜉) - 𝜉 𝑑𝑓(𝜉)/𝑑𝜉]
= 𝑒-𝜉2/2[-𝜉 𝑑𝑓(𝜉)/𝑑𝜉 + 𝜉2𝑓(𝜉) + 𝑑2𝑓(𝜉)/𝑑𝜉2 - 𝑓(𝜉) - 𝜉 𝑑𝑓(𝜉)/𝑑𝜉] = 𝑒-𝜉2/2[𝑑2𝑓(𝜉)/𝑑𝜉2 - 2𝜉 𝑑𝑓(𝜉)/𝑑𝜉 + 𝑓(𝜉)(𝜉2 - 1)].
Plugging this into Eq. 5.72 gives
𝑒-𝜉2/2[𝑑2𝑓(𝜉)/𝑑𝜉2 - 2𝜉 𝑑𝑓(𝜉)/𝑑𝜉 + 𝑓(𝜉)(𝜉2 - 1)] + (𝜖 - 𝜉2)𝑓(𝜉)𝑒-𝜉2/2 = 0 or
(5.73) 𝑒-𝜉2/2[𝑑2𝑓(𝜉)/𝑑𝜉2 - 2𝜉 𝑑𝑓(𝜉)/𝑑𝜉 + 𝑓(𝜉)(𝜖 - 1)] = 0.
Since the equation must be true for all values of 𝜉, the term in square brackets must equal zero:
(5.74) 𝑑2𝑓(𝜉)/𝑑𝜉2 - 2𝜉 𝑑𝑓(𝜉)/𝑑𝜉 + 𝑓(𝜉)(𝜖 - 1) = 0.
This equation is amenable to solution by the power-series approach. First we may write the function 𝑓(𝜉) as a power series:
𝑓(𝜉) = 𝑎0 + 𝑎1𝜉 + 𝑎2𝜉2 + ∙ ∙ ∙ = ∑𝑛=0∞𝑎𝑛𝜉𝑛.
It's customary to start the index at n = 0, so the ground-state wavefunction will be called 𝜓0. The first and second spatial derivatives of 𝑓(𝜉)
𝑑𝑓(𝜉)/𝑑𝜉 = ∑𝑛=0∞𝑛𝑎𝑛𝜉𝑛-1 and 𝑑2𝑓(𝜉)/𝑑𝜉2 = ∑𝑛=0∞𝑛(𝑛-1)𝑎𝑛𝜉𝑛-2
Inserting these into Eq. 5.74 gives
(5.75) ∑𝑛=0∞𝑛(𝑛 - 1)𝑎𝑛𝜉𝑛-2 - 2𝜉∑𝑛=0∞𝑛𝑎𝑛𝜉𝑛-1 + ∑𝑛=0∞𝑎𝑛𝜉𝑛(𝜖 - 1) = 0.
Since at the first summation for which the 𝑛 = 0 and 𝑛 = 1 terms both contribute nothing to the sum, we can simplify the indices by letting 𝑛 → 𝑛+2. So Eq. 5.75 may be written as
∑𝑛=0∞(𝑛 + 2)(𝑛 + 1)𝑎𝑛+2𝜉𝑛 - ∑𝑛=0∞2𝑛𝑎𝑛𝜉𝑛 + ∑𝑛=0∞𝑎𝑛𝜉𝑛(𝜖 - 1) = 0
∑𝑛=0∞[(𝑛 + 2)(𝑛 + 1)𝑎𝑛+2 - 2𝑛𝑎𝑛 + 𝑎𝑛𝜉𝑛(𝜖 - 1)]𝜉𝑛 = 0,
which means that the coefficients of 𝜉𝑛 for each value of 𝑛 must sum to zero:
(𝑛 + 2)(𝑛 + 1)𝑎𝑛+2 - 2𝑛𝑎𝑛 + 𝑎𝑛𝜉𝑛(𝜖 - 1) = 0
(5.76) 𝑎𝑛+2 = [2𝑛 + (1 - 𝜖)]/(𝑛 + 2)(𝑛 + 1) 𝑎𝑛.
This is a recursion relation that relates any coefficient 𝑎𝑛 to the coefficient 𝑎𝑛+2 that is two step higher. If we consider what this equation says about the ratio 𝑎𝑛+2/𝑎𝑛 for large 𝑛. The ratio is
(5.77) 𝑎𝑛+2/𝑎𝑛 = [2𝑛 + (1 - 𝜖)]/(𝑛 + 2)(𝑛 + 1),
and for large values of 𝑛 this ratio converges to
(5.78) 𝑎𝑛+2/𝑎𝑛 = [2𝑛 + (1 - 𝜖)]/(𝑛 + 2)(𝑛 + 1) for large 𝑛 → 2𝑛/(𝑛)(𝑛) = 2/𝑛.
Because 2/𝑛 is exactly what the ratio of the even or odd terms in the power series for the function 𝑒𝜉2 converges to, and if the ratio 𝑎𝑛+2/𝑎𝑛 behaves like 𝑒𝜉2 for large number of 𝑛, then Eq. 5.71 says that the wavefunction 𝜓(𝜉) looks like ※
𝜓(𝜉) = 𝑓(𝜉)𝑒-𝜉2/2 for large 𝑛 → 𝑒𝜉2𝑒-𝜉2/2 = 𝑒+𝜉2/2,
which cannot be normalized if 𝜉 → ∓∞ without any limit. So we must find what condition can cause this series terminate. Accirding to Eq. 5.77 the coefficient 𝑎𝑛+2 equals zero at any value of the energy parameter 𝜖 for which
[2𝑛 + (1 - 𝜖)]/(𝑛 + 2)(𝑛 + 1) = 0. so 2𝑛 + (1 - 𝜖) = 0 and
(5.79) 𝜖 = 2𝑛 + 1.
This means that 𝜖 is quantized, taking on discrete values that depend on the value of 𝑛. Denoting this quantization by using subscript 𝑛, so we have
𝐸𝑛 = 𝜖𝑛(1/2 ℏ𝜔) = (2𝑛 + 1)(1/2 ℏ𝜔) or
(5.80) 𝐸𝑛 = (𝑛 + 1/2)ℏ𝜔.
These are the allowed value for the energy of a quantum harmonic oscillator. So the ground-state energy is 𝐸0 = (1/2)ℏ𝜔, which is exactly what was used as 𝐸𝑟𝑒𝑓 in Eq. 5.62. Each energy level 𝐸𝑛 is precisely ℏ𝜔 higher than the adjacient lower level 𝐸𝑛-1.
From this point foward the summation index for wavefunction will be labeled as 𝑚 like this:
(5.81) 𝑓(𝜉) = ∑𝑚=0,1,2... 𝑎𝑚𝜉𝑚.
It's helpful to separate this into two series - one with the even powers and the other with the odd power:
(5.82) 𝑓(𝜉) = ∑𝑚=0,2.4... 𝑎𝑚𝜉𝑚 + ∑𝑚=1,3.5... 𝑎𝑚𝜉𝑚.
We know that the summation terminates whenever the energy parameter 𝜖𝑛takes on the value 2𝑛 + 1. Plugging this into Eq. 5.76
(5.83) 𝑎𝑚+2 = [2𝑚 + (1 - 𝜖𝑛)]/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = [2𝑚 + (1 - (2𝑛 + 1)]/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚,
which means the series terminates when 𝑚 = 𝑛. When 𝑚 = 𝑛 = 0 (so all even term with 𝑚 > 𝑛 are zero), To ensure all the odd terms zero we must set 𝑎1 = 0. So the function 𝑓0(𝜉) is
(5.84) 𝑓0(𝜉) = ∑𝑚=0 only 𝑎𝑚𝜉𝑚 = 𝑎0𝜉0 = 𝑎0.
Now consider the first excited (𝑛 = 1) case (so all odd term with 𝑚 > 𝑛 are zero). And to make sure that the even series doesn't blow up we must set 𝑎0 = 0. So the function 𝑓1(𝜉) for the first excited states is
(5.85) 𝑓1(𝜉) = ∑𝑚=1 only 𝑎𝑚𝜉𝑚 = 𝑎1𝜉1 = 𝑎1𝜉.
For the second excited state 𝑛 = 2, the energy parameter 𝜖2 = 5, and even series terminates at 𝑚 = 𝑛 = 2. But in this case the counter 𝑚 can take on 0 and 2. For 𝑚 = 0 and 𝑛 = 2, the recursion relation gives
𝑎2 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(0 - 2)/(0 + 2)(0 + 1) 𝑎0 = -2𝑎0,
and for 𝑚 = 2 and 𝑛 = 2, the recursion relation gives
𝑎2 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(2 - 2)/(2 + 2)(2 + 1) 𝑎0 = 00, so
(5.86) 𝑓2(𝜉) = ∑𝑚=0 and 2 𝑎𝑚𝜉𝑚 = 𝑎0𝜉0 + 𝑎2𝜉2 = (𝑎0 + 𝑎2𝜉2) = 𝑎0(1 - 2𝜉2).
For the third excited states 𝑛 = 3, 𝜖3 = 7, and the odd series terminates at 𝑚 = 𝑛 = 3. In this case the counter 𝑚 can take on the values of 1 and 3. For 𝑚 = 1 and 𝑛 = 3
𝑎3 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(1 - 3)/(1 + 2)(1 + 1) 𝑎0 = -2/3 𝑎1,
For 𝑚 = 3 and 𝑛 = 3
𝑎5 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(3 - 3)/(2 + 2)(2 + 1) 𝑎2 =0, Hence
(5.87) 𝑓3(𝜉) = ∑𝑚=1 and 3 𝑎𝑚𝜉𝑚 = 𝑎1𝜉1 + 𝑎3𝜉3 = (𝑎1𝜉 + 𝑎2𝜉3) = 𝑎1(𝜉 - 2/3 𝜉3).
For the fourth excited states 𝑛 = 4, 𝜖4 = 9, and the even series terminates at 𝑚 = 𝑛 = 4. In this case the counter 𝑚 can take on the values of 0, 2 and 4. For 𝑚 = 0 and 𝑛 = 4
𝑎2 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(0 - 4)/(0 + 2)(0 + 1) 𝑎0 = -4𝑎0,
For 𝑚 = 2 and 𝑛 = 4
𝑎4 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(2 - 4)/(2 + 2)(2 + 1) 𝑎2 = -4/12 𝑎2 = -1/3 𝑎2 = 4/3 𝑎0,
Finally for 𝑚 = 4 and 𝑛 = 4
𝑎6 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(4 - 4)/(4 + 2)(4 + 1) 𝑎2 = 0, Hence
(5.88) 𝑓4(𝜉) = ∑𝑚=0,2 and 4 𝑎𝑚𝜉𝑚 = 𝑎0𝜉0 + 𝑎2𝜉2 + 𝑎4𝜉4 = 𝑎0(1 - 4𝜉2 + 4/3 𝜉4).
For the fifth excited states 𝑛 = 5, 𝜖4 = 11, and the even series terminates at 𝑚 = 𝑛 = 5. In this case the counter 𝑚 can take on the values of 1, 3 and 5. For 𝑚 = 1 and 𝑛 = 5
𝑎3 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(1 - 5)/(1 + 2)(1 + 1) 𝑎1 = -4/3 𝑎1,
For 𝑚 = 3 and 𝑛 = 5
𝑎5 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(3 - 5)/(3 + 2)(3 + 1) 𝑎2 = -4/20 𝑎3 = -1/5 𝑎3 = 4/15 𝑎1,
Lastly for 𝑚 = 5 and 𝑛 = 5
𝑎6 = 2(𝑚 - 𝑛)/(𝑚 + 2)(𝑚 + 1) 𝑎𝑚 = 2(5 - 5)/(5 + 2)(5 + 1) 𝑎5 = 0, Thus
(5.89) 𝑓5(𝜉) = ∑𝑚=1,3 and 5 𝑎𝑚𝜉𝑚 = 𝑎1𝜉1 + 𝑎3𝜉3 + 𝑎5𝜉5 = 𝑎1(𝜉 - 4/3 𝜉3 + 4/15 𝜉5).
Now in order to relate to the Hermite polynomials mentioned earlier we may arrange the 𝑓𝑛 functions to pull out the constant needed to cause the numerical factor in front of the highest power of 𝜉 for each value of 𝑛 to be 2𝑛. That looks like this:
𝑓0(𝜉) = 𝑎0 = 𝑎0(1)
𝑓1(𝜉) = 𝑎1𝜉 = 𝑎1/2(2𝜉)
𝑓2(𝜉) = 𝑎0(1 - 2𝜉2) = -𝑎0/2 (4𝜉2 - 2)
𝑓3(𝜉) = 𝑎1(𝜉 - 2/3 𝜉3) = -𝑎1/12 (8𝜉3 - 12𝜉)
𝑓4(𝜉) = 𝑎0(1 - 4𝜉2 - 4/3 𝜉4) = 𝑎0/12 (16𝜉4 - 48𝜉3 + 12)
𝑓5(𝜉) = 𝑎1(𝜉 - 4/3 𝜉3 + 4/15 𝜉5) = 𝑎1/120 (32𝜉5 - 160𝜉3 + 120𝜉).
Referring to mathematical handbook we can find these expression:
𝐻0(𝜉) = 1 𝐻1(𝜉) = 2𝜉 𝐻2(𝜉) = 4𝜉2 - 2
𝐻3(𝜉) = 8𝜉3 - 12𝜉 𝐻4(𝜉) = 16𝜉4 - 48𝜉3 + 12 𝐻5(𝜉) = 32𝜉5 - 160𝜉3 + 120𝜉.
So calling the constant factors involving 𝑎0 or 𝑎1 in 𝑓𝑛(𝜉) 𝐴𝑛 Eq. 5.71 gives
(5.90) 𝜓𝑛(𝜉) = 𝑓𝑛(𝜉)𝑒-𝜉2/2 = 𝐴𝑛𝐻𝑛(𝜉)𝑒-𝜉2/2,
where constants will be determined later by normalizing the wavefunction 𝜓𝑛(𝜉).
The quantum harmonic oscillator wavefunctions are comprised of the product of Hermite polynomials 𝐻𝑛 and a Gaussian function 𝑒-𝜉2/2. The Gaussian term that causes wavefunction 𝜓(𝜉) to decrease toward zero as 𝜉 goes to ∓∞, providing the spatial localization for normalization.
To accomplish that normalization, set the integrated probability density over all space to unity. For 𝜓𝑛(𝑥), the integration is over 𝑥:
(5.91) ∫-∞∞ 𝜓*(𝑥)𝜓(𝑥) 𝑑𝑥 = 1,
and Eq. 5.66 relates 𝑑𝑥 to 𝑑𝜉, so
(5.92) ∫-∞∞ 𝜓*(𝑥)𝜓(𝑥) 𝑑𝑥 = √(ℏ/𝑚𝜔) ∫-∞∞ 𝜓*(𝜉)𝜓(𝜉) 𝑑𝜉, which means
(5.93) √(ℏ/𝑚𝜔) ∫-∞∞ [𝐴𝑛𝐻𝑛(𝜉)𝑒-𝜉2/2]*[𝐴𝑛𝐻𝑛(𝜉)𝑒-𝜉2/2] 𝑑𝜉 = 1, or
(5.94) √(ℏ/𝑚𝜔) ∣𝐴𝑛∣2 ∫-∞∞ ∣𝐻𝑛(𝜉)∣2𝑒-𝜉2/2 𝑑𝜉 = 1.
But mathematicans works on weber equation and Hermite polynomials have given us a very neat integral identity: ※
(5.95) ∫-∞∞ ∣𝐻𝑛(𝜉)∣2𝑒-𝜉2/2 𝑑𝜉 = 2𝑛𝑛!(π1/2).
Inserting this expression into Eq. 5.94 yields
√(ℏ/𝑚𝜔) ∣𝐴𝑛∣22𝑛𝑛!(π1/2) = 1 ∣𝐴𝑛∣22 = √(𝑚𝜔/ℏ) 1/[22𝑛𝑛!(π1/2)],
and taking the square root gives the normalization constant 𝐴𝑛:
(5.96) ∣𝐴𝑛∣ = (𝑚𝜔/ℏ)1/4 1/√[2𝑛𝑛!(π1/2)] = (𝑚𝜔/πℏ)1/4 1/√(2𝑛𝑛!).
With 𝐴𝑛 in hand, we can write the wavefunction 𝜓𝑛(𝜉) as
(5.97) 𝜓𝑛(𝜉) = (𝑚𝜔/πℏ)1/4 (1/√(2𝑛𝑛!) 𝐻𝑛(𝜉)𝑒-𝜉2/2.
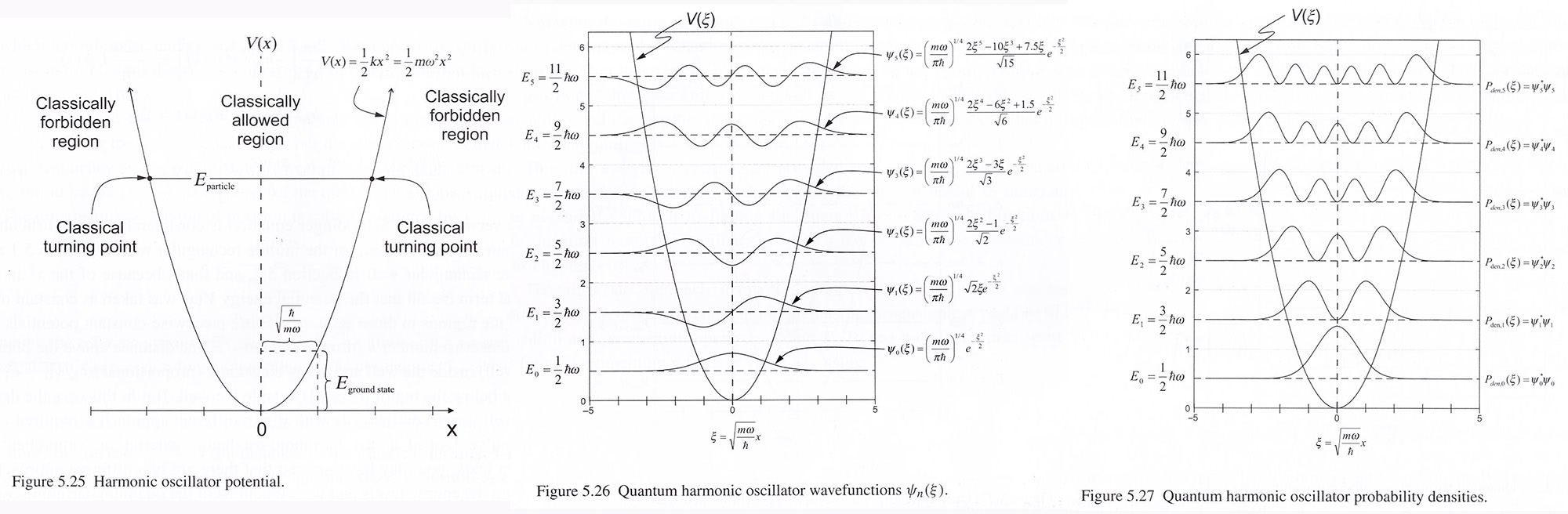
These wavefntions 𝜓𝑛(𝜉) for six lowest energy levels of the quantum harmonic oscillator are shown in Fig. 5.26. We can compare it with the solutions in the finite rectangular well, which are also oscillatory in the classically allowed region and exponentially decaying in the classically forbidden regions.In the classically allowed region.
the probability densities 𝑃𝑑𝑒𝑛(𝜉) = 𝜓𝑛*(𝜉)𝜓𝑛(𝜉) for the six lowest energy wavefunctions of the harmonic oscillator are shown in Fig. 5.27. At low energies the behavior of quantum harmonic oscillator differs significantly from the classical case. However as 𝑛 increases, the behavior of the quantumn harmonic oscillator does begin to resemble that of the classical case at large values of 𝑛, as required the Correspondence Principle described in Section 4.1.
We should also bear in mind that these wavefunctions are the eigenfunctions of the Hamiltonian operator achieved by separation of variables, so they represent stationary states for which the expectation values of observables such as position, momentum, and energy do not change over time. To determine the behavior of particles in other states, we must include the time function 𝑇(t), shich makes 𝜓𝑛(𝑥, 𝑡) ※
(5.97) 𝜓𝑛(𝑥, 𝑡) = (𝑚𝜔/πℏ)1/4 (1/√(2𝑛𝑛!) 𝐻𝑛[√(𝑥𝑚𝜔/ℏ)]𝑒-𝑥2𝑚𝜔/2ℏ𝑒-𝑖(𝑛 + 1/2)𝜔𝑡.
Knowing the allowed energy levels 𝐸𝑛 and wavefunctions 𝜓𝑛(𝑥, 𝑡) allows us to determine the quantum harmonic oscillator over space and time. Thus the analytic approach has provided the tools we need to analize this important configuration. But we may also find it useful to understand the algebraic approach to find the energy leves and wavefunctions for the quantum harmonic oscillator.
The algebraic approach involves a dimensionless version of Schrödinger equation using dimensionless versions of position and momentum operators 𝑋^ and 𝑃^. Starting by defining a momentum reference value 𝑝𝑟𝑒𝑓 using
𝑝𝑟𝑒𝑓2/2𝑚 = 𝐸𝑟𝑒𝑓 = 1/2 ℏ𝜔 𝑝𝑟𝑒𝑓 = √(𝑚ℏ𝜔),
we produce a dimensionless version of momentum called 𝓟 as
(5.99, 100) 𝓟 = 𝑝/𝑝𝑟𝑒𝑓 = 𝑝/√(𝑚ℏ𝜔) or 𝑝 = 𝓟(𝑝𝑟𝑒𝑓/).
To produce a dimensionless version of the TISE, we should write energy 𝐸 in terms of dimensionless energy 𝜖, position 𝑥 in terms of dimensionless position 𝜉, and momentum 𝑝 in terms of dimensionless momentum 𝓟. The TISE from Chapter 3:
(3.40) -(ℏ2/2𝑚) 𝑑2[𝜓(𝑥)]/𝑑𝑥2 + 𝑉[𝜓(𝜉)] = 𝐸[𝜓(𝜉)],
which can be written in terms of the momentum operator 𝑃^ and position operator 𝑋^ for quantum harmonic oscillator as ※
[𝑃^2/2𝑚 + 1/2 𝑚𝜔^2𝑋^2][𝜓(𝑥)] = 𝐸[𝜓(𝑥)],
Using dimensionless operators 𝓟^ = 𝑃^/𝑝𝑟𝑒𝑓 and 𝜉^ = 𝑋^/𝑥𝑟𝑒𝑓 makes this
[[𝓟^ (𝑝𝑟𝑒𝑓)]2/2𝑚 + 1/2 𝑚𝜔^2[𝜉^ (𝑥𝑟𝑒𝑓)]2][𝜓(𝑥)] = 𝜖(𝐸𝑟𝑒𝑓)[𝜓(𝜉)], or
[[𝓟^ √(𝑚ℏ𝜔)]2/2𝑚 + 1/2 𝑚𝜔^2[𝜉^ √(ℏ/𝑚𝜔)]2][𝜓(𝜉)] = 𝜖(1/2 ℏ𝜔)[𝜓(𝜉)] [𝓟^2ℏ𝜔/2 + 𝜉^2ℏ𝜔/2][𝜓(𝜉)] = 𝜖(1/2 ℏ𝜔)[𝜓(𝜉)]. So we have
(5.101) [𝓟^2 + 𝜉^2][𝜓(𝜉)] = 𝜖[𝜓(𝜉)].
To solve this equation we begin with two new operators, which are combinations of the dimensionless position and momentum operators. The first one is
(5.101) 𝑎^† = 1/√2 (𝜉^ - 𝑖𝓟^) and the second one is
(5.102) 𝑎^ = 1/√2 (𝜉^ + 𝑖𝓟^).
Their product is
𝑎^†𝑎^ = 1/√2 (𝜉^ - 𝑖𝓟^) 1/√2 (𝜉^ + 𝑖𝓟^) = 1/2 (𝜉^2 + 𝑖𝜉^𝓟^ - 𝑖𝓟^𝜉^ + 𝓟^2).
(5.104) 𝑖𝜉^𝓟^ - 𝑖𝓟^𝜉^ = 𝑖(𝜉^𝓟^ - 𝓟^𝜉^) = 𝑖[𝜉^, 𝓟^],
where [𝜉^, 𝓟^] represents the commutator of the operators 𝜉^ and 𝓟^. Thhis makes the product 𝑎^†𝑎^ looks like this:
(5.105) 𝑎^†𝑎^ = 1/2(𝜉^2 + 𝓟^2 + 𝑖[𝜉^, 𝓟^]).
This can be simplified by writing the commutator in terms of 𝑋^ and 𝑃^.
𝑖[𝜉^, 𝓟^] = 𝑖[𝑋^/𝑥𝑟𝑒𝑓, 𝑃^/𝑝𝑟𝑒𝑓] = 𝑖/𝑥𝑟𝑒𝑓𝑝𝑟𝑒𝑓 [𝑋^, 𝑃^] or
𝑖[𝜉^, 𝓟^] = 𝑖/√(ℏ/𝑚𝜔)√(𝑚ℏ𝜔) [𝑋^, 𝑃^] = 𝑖/ℏ [𝑋^, 𝑃^].
Recall from Chapter 4 that the canonical communication relation Eq. 4.68 tells us that [𝑋^, 𝑃^] = 𝑖ℏ, which means
(5.106) 𝑖[𝜉^, 𝓟^] = 𝑖/ℏ [𝑖ℏ] = -1.
Plugging this into Eq. 5.105 gives
(5.107) 𝑎^†𝑎^ = 1/2(𝜉^2 + 𝓟^2 - 1) or (𝜉^2 + 𝓟^2) = 2𝑎^†𝑎^ + 1.
This makes the TISE Eq. 5.101
[𝓟^2 + 𝜉^2][𝜓(𝜉)] = (2𝑎^†𝑎^ + 1)[𝜓(𝜉)] = 𝜖[𝜓(𝜉)] or 2𝑎^†𝑎^[𝜓(𝜉)] = (𝜖 - 1)[𝜓(𝜉)].
Plugging the definition of 𝑎^† and 𝑎^ into this equation gives
(5.108) 2[{1/√2 (𝜉^ - 𝑖𝓟^)}{1/√2 (𝜉^ + 𝑖𝓟^)}][𝜓(𝜉)] = (𝜖 - 1)[𝜓(𝜉)] or (𝜉^ - 𝑖𝓟^)(𝜉^ + 𝑖𝓟^) = (𝜖 - 1)[𝜓(𝜉)].
One way that this equation can be satisfied is for 𝜖 = 1 while 1/√2 (𝜉^ + 𝑖𝓟^)[𝜓(𝜉)] = 0.
So if 𝜖 = 1, the total energy is
𝐸 = 𝜖𝐸𝑟𝑒𝑓 = (1)(ℏ𝜔/2) = 1/2 ℏ𝜔,
in agreement which 𝐸0 determined by the analytical approach in Eq. 5.80. If (𝜉^ + 𝑖𝓟^)[𝜓(𝜉)] = 0, the momentum operators 𝑃^ and 𝓟^ is from Eq. 3.29, Eq. 5.66, and Eq. 5.99
𝑃^ = -𝑖ℏ 𝑑/𝑑𝑥 = -𝑖ℏ 𝑑/[√(ℏ/𝑚𝜔) 𝑑𝜉] = -𝑖√(𝑚ℏ𝜔) 𝑑/𝑑𝜉 and 𝓟^ = 𝑃^/𝑃𝑟𝑒𝑓 = -𝑖√(𝑚ℏ𝜔)/√(𝑚ℏ𝜔) 𝑑/𝑑𝜉 = -𝑖𝑑/𝑑𝜉, then
(5.109) (𝜉^ + 𝑖𝓟^)[𝜓(𝜉)] = [𝜉 + 𝑖(-𝑖𝑑/𝑑𝜉)][𝜓(𝜉)] = 0 [𝜉 + 𝑑/𝑑𝜉][𝜓(𝜉)] = 0 𝑑𝜓(𝜉)/𝑑𝜉 = -𝜉𝜓(𝜉).
The solution is this equation is 𝜓(𝜉) = 𝐴𝑒-𝜉2/2, and normalizing gives 𝐴 = (𝑚𝜔/πℏ)1/4.※
Hence the algebraic approach gives the lowest-energy eigenfunction
𝜓0(𝜉) = (𝑚𝜔/πℏ)1/4 𝑒-𝜉2/2,
exactly as found for 𝜓0(𝜉) using the analytic approach.
The operator 𝑎^† and 𝑎^ also useful individually. We can see this by applying the 𝑎^† to 𝜓0(𝜉):
𝑎^†𝜓0(𝜉) = 1/√2 (𝜉^ - 𝑖𝓟^)[(𝑚𝜔/πℏ)1/4 𝑒-𝜉2/2] = 1/√2 (𝑚𝜔/πℏ)1/4 [𝜉𝑒-𝜉2/2 - 𝑑/𝑑𝜉(𝑒-𝜉2/2)] = (𝑚𝜔/πℏ)1/4[√2𝜉𝑒-𝜉2/2] = 𝜓1(𝜉).
For this reason 𝑎^† is known as a "raising" operator. For the raising operator, the constant of proportionality is √(𝑛 + 1), so
(5.110) 𝑎^†𝜓𝑛(𝜉) = √(𝑛 + 1)𝜓𝑛+1(𝜉).
Also the operator 𝑎^ performs the complementary function, producinga wavefunction proportional to the wavefunction with the quantum number lowered by one. Hence 𝑎^ is called a "lowering operator", and for the lowering oprator, the constant of proportionality is √𝑛. Thus
(5.111) 𝑎^𝜓𝑛(𝜉) = √𝑛 𝜓𝑛-1(𝜉).
This is why 𝑎^† and 𝑎^ are known as ladder operators; they alloe us to "climb" up or down the wavefunctions of the quantum harmonic oscillator. Some texts refer to the ladder operators as "creation" and "annihilation" oprators - each step up creates and each set down destroys one quantum (1/2 ℏ𝜔) of energy.
* Textbook: Daniel A. Fleisch A Student's Guide to the Schrödinger Equation (Cambridge University Press 2020)
※ attention: some rigorous derivation might be required
p.s. 동일 저자의 인기 저서인 Maxwell's Equation (2008) [59], Vectors and Tensors (2012) [82]에 이은 세번째 책
앞에서 언급했듯이 Mathematics of Astronomy (2013)도 읽었는데, 모두 천체물리학 초보/독학자들에게 강력히 추천함.
학습 후 1년 지나서 번역판을 발견함..ㅎ <슈뢰딩거 방정식> (Daniel A. Fleisch, 최준곤 옮김, 학산미디어 2020)
|
|
|





































