|
김관석
|
2020-06-07 01:21:03, 조회수 : 1,060 |
- Download #1 : Math_Cos_2.jpg (169.7 KB), Download : 1

14. The Friedmann-Robertson-Walker geometry* .
14.1 The cosmological principle .
We have good evidence that the universe is isoptropic on the very larges scales, to high accuarcy. If the universe has no prefered center then isotropy also implies homogeneity. We assume the cosmological principle, which states that at any particular time, the universe the same from all positions in space and all directions in space at any point are equivalent.
4.2 Slicing and threading spacetime .
In general relativity the concept of a 'moment of time' is ambiguous and is replaced the notion of a three-dimensional spacelike hypersurface. To define a 'time' parameter we slice 'slice up' spacetime by introducing a series of non-intersecting spacelike hypersurfaces that are labelled by some parameter 𝑡. This parameter then defines a universal time in that 'particular time' means a given hypersurface.
It is useful at this point to introduce the idealized concept of fundamental observers, who are assumed to have no motion relative to the overall cosmological fluid associated with the 'smeared-out' motion of all the galaxies and other matter in the universe. Whe we adopt Weyl's postulate (1923) asumming that the worldlines of galaxies are a bundle or congruence of geodesics in spacetime diverging from a point in the finite or infinitely distant past or future or both, the worldline means the timelike worldline of the fundamental observer. The set of worldlines is sometimes described as providing threading for the spacetime.
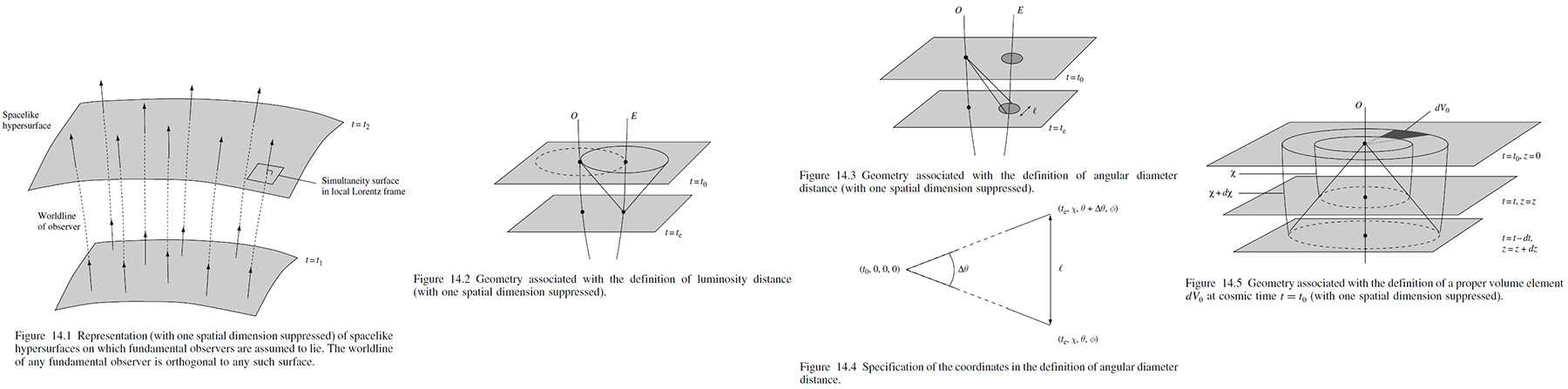
The hypersurfaces 𝑡 = constant may now be naturally constructed in such a way that the 4-velocity of any fundamental observer is orthogonal to the hypersurface. Thus, the surface of simultaneity of the local Lorentz frame of any such observer coincides locally with the hypersurface (see Figure 14.1). Each hypersurface may therefore be considered as the 'meshing together' of all the local Lorentz frames of the fundamental observers.
14.3 Syncronous comoving coordinates .
The spacelike hypersurfaces are labelled by a parameter 𝑡, which may be taken to be the proper time along the worldline. The parameter 𝑡 is the called the synchronous time coordiniate or cosmic time. In addition, we may introduce spatial coordinates (𝑥1, 𝑥2, 𝑥3) that are constant along the worldline. Thus each fundamental observer has fixed (𝑥1, 𝑥2, 𝑥3) coordinates, and is called comoving coordinates. The line element takes the form
(14.1) 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑔𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗 (𝑖,𝑗 = 1,2,3),
where the 𝑔𝑖𝑗 are functions of the coordinates (𝑡, 𝑥1, 𝑥2, 𝑥3).
Let 𝑥𝜇(𝜏) be the worldline of a fundamental observer, where 𝜏 is the proper time along the worldline. Then, by construction, 𝑥𝜇(𝜏) is given by
(14.2) 𝑥0 = 𝜏, 𝑥1 = constant, 𝑥2 = constant, 𝑥3 = constant.
Since 𝑑𝑥𝑖 = 0 along the worldline, we obtain 𝑑𝑠 = 𝑐 𝑑𝜏 = 𝑐 𝑑𝑡 and so 𝑡 = 𝜏. Thus, from (3.2) the 4-velocity of a fundamental observer in comoving coordinates is
(14.3) [𝑢𝜇] = [𝑑𝑥𝜇/𝑑𝜏] = (1, 0, 0, 0).
Since any vector lying in the hypersurface t = constant has the form [𝑎𝜇] = [0, 𝑎1, 𝑎2, 𝑎3). we see that
𝑔𝜇𝜈𝑢𝜇𝑎𝜈 = 0,
because 𝑔0𝑖 = 0 for 𝑖 = 1,2,3. Hence the observer's 4-velocity is orthogonal to hypersurface. Finally, we may show that the worldline given by (14.2) satisfies the geodesic equation
𝑑𝑠2𝑥𝜇/𝑑𝜏2 + 𝛤𝜇𝜈𝜎 𝑑𝑥𝜇/𝑑𝜏 𝑑𝑥𝜎/𝑑𝜏 = 0.
Using (3.3), we see that we require only that 𝛤𝜇00 = 0. This quantity is given by
𝛤𝜇00 = 1/2 𝑔𝜇𝜈(2𝑔0𝜈,0 - 𝑔00,𝜈),
which is easily shown to be zero by using the fact that 𝑔0𝑖 = 0 for 𝑖 = 1,2,3. Thus the worldline 𝑥𝜇(𝜏) are geodesics and hence can describe particles (observers) moving only under the influence of gravity.
14.4 Homogeneity and isotropy of the universe .
The metric (3.1) does not yet incorporate the property that space is homogeneous and isotropic.
Let us now incorporate the postulates of homogenitey and isotropy. The (squared) spatial separation on the same hypersurface 𝑡 = constant of two nearby galaxies at coordinates (𝑥1, 𝑥2, 𝑥3) and (𝑥1 + 𝛥𝑥1, 𝑥2 + 𝛥𝑥2, 𝑥3 + 𝛥𝑥3) is
𝑑𝜎2 = 𝑔𝑖𝑗𝛥𝑥𝑖𝛥𝑥𝑗.
If we consider the triangle formed by three nearby galaxies at some particular time 𝑡, then isotropy requires that the triangle at some later time must be similar to the original triangle. Moreover the homogeneity requires that he magnification factor must be indepenent of the position of the triangle in the 3-space.It follows that time 𝑡 can enter the 𝑔𝑖𝑗 only trough a common factor, so that the ratios of small distances are the same at all times, Hence the metric must take the form
(14.4) 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑆2(𝑡)𝘩𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗,
where 𝑆(𝑡) is a time-dependent scale factor and the 𝘩𝑖𝑗 are the functions of the coordinates (𝑥1, 𝑥2, 𝑥3) only. since the magnification factor are independent of position, we must neglect the small peculiar velocities of real individual galaxies.
14.5 The maximally symmetric 3-space .
We clearly require the 3-space spanned by the spacelike coordinates (𝑥1, 𝑥2, 𝑥3) to be homogeneous and isotropic. This leads us to study the maximally symmetic 3-space. A maximally symmetric space is specified by the curvature K, which is independent of the coordinates. Such constant curvature spaces must clearly be homogeneous and isotropic.
The simplest expression that satisfies the various symmetry properties and identities of 𝑅𝑖𝑗𝑘𝑙 and contains just 𝐾 and the metric tensor is given by
(14.5) 𝑅𝑖𝑗𝑘𝑙 = 𝐾(𝑔𝑖𝑘𝑔𝑗𝑙 - 𝑔𝑖𝑙𝑔𝑗𝑘),
which is the definition of a maximally symmetric space.
The Ricci tensor and Ricci scalar are given as follows
𝑅𝑗𝑘 = 𝑔𝑖𝑙𝑅𝑖𝑗𝑘𝑙 = 𝐾𝑔𝑖𝑙(𝑔𝑖𝑘𝑔𝑗𝑙 - 𝑔𝑖𝑙𝑔𝑗𝑘) = 𝐾(𝛿𝑙𝑘𝑔𝑗𝑙 - 𝛿𝑙𝑙𝑔𝑗𝑙𝑔𝑗𝑘) = 𝐾(𝑔𝑗𝑘 - 3𝑔𝑗𝑙𝑔𝑗𝑘) = -2𝐾𝑔𝑗𝑘.
𝑅 = 𝑅𝑘𝑘 = -2𝐾𝛿𝑘𝑘 = -6𝐾.
The metric of an isotropic 3-space must depend only on the rotational invariants
𝐱 ⋅ 𝐱 ≡ 𝑟2, 𝑑𝐱 ⋅ 𝑑𝐱, 𝐱 ⋅ 𝑑𝐱,
and in spherical polar coordinates (𝑟, 𝜃, 𝜙) it must take the form
𝑑𝜎2 = 𝐶(𝑟)(𝐱 ⋅ 𝑑𝐱)2 + 𝐷(𝑟)(𝑑𝐱 ⋅ 𝑑𝐱)2 = 𝐶(𝑟)𝑟2𝑑𝑟2 + 𝐷(𝑟)(𝑑𝑟2 + 𝑟2𝑑𝜃2 + 𝑟2sin2𝜃 𝑑𝜙2) = 𝐵(𝑟)𝑑𝑟2 + 𝑟2𝑑𝜃2 + 𝑟2sin2𝜃 𝑑𝜙2,
where 𝐵(𝑟) is an arbitrary function of 𝑟.
The above line element is identical to the space part of Schwartzschild metric. The only non-zero connection coefficients are
𝛤𝑟𝑟𝑟 = 1/2𝐵(𝑟) 𝑑𝐵(𝑟)/𝑑𝑟, 𝛤𝑟𝜃𝜃 = -𝑟/𝐵(𝑟), 𝛤𝑟𝜙𝜙 = -𝑟sin2𝜃/𝐵(𝑟), 𝛤𝜃𝑟𝜃 = 𝛤𝜙𝑟𝜙 = 1/𝑟, 𝛤𝜃𝜙𝜙 = -sin 𝜃 cos 𝜃, 𝛤𝜙𝜙𝜃 = cot 𝜃,
The Ricci tensor in terms of connection coefficients and non-zero components are
𝑅𝑖𝑗 = 𝛤𝑘𝑖𝑘,𝑗 - 𝛤𝑘𝑖𝑗,𝑘 + 𝛤𝑘𝑖𝑘 𝛤𝑘𝑖𝑗 - 𝛤𝑙𝑖𝑗 𝛤𝑘𝑙𝑘,
𝑅𝑟𝑟 = -1/𝑟𝐵 𝑑𝐵/𝑑𝑟, 𝑅𝜃𝜃 = 1/𝐵 - 1 - 𝑟/2𝐵2 𝑑𝐵/𝑑𝑟, 𝑅𝜙𝜙 = 𝑅𝜃𝜃 sin2𝜃
Since 𝑅𝑖𝑗 = -2𝐾𝑔𝑖𝑗, so we get following equations
(14.6) 1/𝑟𝐵 𝑑𝐵/𝑑𝑟 = 2𝐾𝐵(𝑟), ∴ 𝐵(𝑟) = 1/(𝛢 - 𝐾𝑟2)
(14.7) 1+ 𝑟/2𝐵2 𝑑𝐵/𝑑𝑟 - 1/𝐵 = 2𝐾𝑟2. 1 - 𝛢 + 𝐾𝑟2 = 𝐾𝑟2, ∴ 𝛢 = 1
(14.8) 𝑑𝜎2 = 𝑑𝑟2/(1 - 𝐾𝑟2) + 𝑟2𝑑𝜃2 + 𝑟2sin2𝜃 𝑑𝜙2,**
which is the line element for the maximally symmetric 3-space with one number, 𝐾, the curvature of the space and the metric for a 3-sphere embedded in four-dimensional Euclidean space. The metric contains a 'hidden symmetry', since the origin of the radial coordinate is completely arbitrary. We can choose any point in this space as our origin since all points are equivalent.
14.6 The Friedmann-Robertson-Walker metric .
Combining the line element (3.4) for cosmological principle and Weyl's postulate and equation (3.8) we obtain
(14.9) 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑆2(𝑡)[𝑑𝑟2/(1 - 𝐾𝑟2) + 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)].
If we define 𝑘 = 𝐾/∣𝐾∣ and introduce the rescaled coordinates 𝑟̄ = ∣𝐾∣1/2𝑟, then (3.9) becomes
𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑆2(𝑡)/∣𝐾∣[𝑑𝑟2/(1 - 𝑘𝑟2) + 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)].
Finally, we define a rescaled scale function 𝑅(𝑡) by
𝑅(𝑡) = {𝑆(𝑡)/∣𝐾∣1/2 if 𝐾 ≠ 0, 𝑆(𝑡) if 𝐾 = 0}
Then, dropping the bars on the radial coorrdinates, we obtain the standard form for the Friedmann-Robertson-Walker (FRW) line elements,
(14.10) 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑅2(𝑡)[𝑑𝑟2/(1 - 𝑘𝑟2) + 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
where 𝑘 takes the values -1, 0, or 1 depending on whether the spatial section has negative, zero or positive curvature respectively.
14.7 Geometric properties of the FRW metric .
[Positive spatial curvature: 𝑘 = 1]
In this case, because the coefficient of 𝑑𝑟 in FRW metric becomes singular as 𝑟 → 1, we introduce a new radial coordinates 𝜒 as follows
𝑟 = sin 𝜒 ⇒ 𝑑𝑟 = cos 𝜒 𝑑𝜒 = (1 - 𝑟2)1/2𝑑𝜒
𝑑𝜎2 = 𝑅2[𝑑𝜒2 + sin2𝜒 (𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
Consider the 3-space as embedded in a four-dimensional Euclidean space with coordinates (𝑤, 𝑥, 𝑦, 𝑧) given by
𝑤 = 𝑅 cos 𝜒, 𝑥 = 𝑅 sin 𝜒 sin 𝜃 cos 𝜙, 𝑦 = 𝑅 sin 𝜒 sin 𝜃 sin 𝜙, 𝑧 = 𝑅 sin 𝜒 cos 𝜃;
𝑤2 + 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2,
𝑑𝜎2 = 𝑑𝑤2 + 𝑑𝑥2 + 𝑑𝑦2 + 𝑑𝑧2 = 𝑅2[𝑑𝜒2 + sin2𝜒 (𝑑𝜃2 + sin2𝜃 𝑑𝜙2)].
Consider again at a particular time 𝑡 the 2-surface given by 𝜒 = constant, whence we get 𝑤 = 𝑅 cos 𝜒, and
𝑥2 + 𝑦2 + 𝑧2 = 𝑅2 sin2 𝜒
This behaviour is similar to what happen on a 2-sphere in a three-dimensional Euclidean space. When 𝜒 = constant, The surface area 𝛢 and a finite total volume 𝑉 are given as follows,
𝛢 = ∫π𝜃=0∫2π𝜙=0 (𝑅 sin 𝜒 𝑑𝜃)(𝑅 sin 𝜒 sin 𝜃 𝑑𝜙) = 4π𝑅2 sin2𝜒,
𝑉 = ∫π𝜒=0∫π𝜃=0∫2π𝜙=0 (𝑅 𝑑𝜒)(𝑅 sin 𝜒 𝑑𝜃)(𝑅 sin 𝜒 sin 𝜃 𝑑𝜙) = 2π2𝑅3,
where 𝑅 is often referred to as the 'radius of the universe'.
[Zero spatial curvature: 𝑘 = 0]
In this case, if we set 𝑟 = 𝜒, the 3-space line element is simply the ordinary three-dimensional Euclidean space as follows,
𝑑𝜎2 = 𝑅2[𝑑𝜒2 + 𝜒2 (𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
𝑥 = 𝑅𝜒 sin 𝜃 cos 𝜙, 𝑦 = 𝑅𝜒 sin 𝜃 sin 𝜙, 𝑧 = 𝑅𝜒 cos 𝜃;
𝑑𝜎2 = 𝑥2 + 𝑦2 + 𝑧2.
[Negative spatial curvature: 𝑘 = -1]
In this case, we introduce a new radial coordinates 𝜒 given by
𝑟 = sinh 𝜒 ⇒ 𝑑𝑟 = cosh 𝜒 𝑑𝜒 = (1 + 𝑟2)1/2𝑑𝜒
𝑑𝜎2 = 𝑅2[𝑑𝜒2 + sinh2𝜒 (𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
which is embedded in a four-dimensonal Minkowski space with coordinates (𝑤, 𝑥, 𝑦, 𝑧) given by
𝑤 = 𝑅 cosh 𝜒, 𝑥 = 𝑅 sinh 𝜒 sin 𝜃 cos 𝜙, 𝑦 = 𝑅 sinh 𝜒 sin 𝜃 sin 𝜙, 𝑧 = 𝑅 sinh 𝜒 cos 𝜃;
𝑑𝜎2 = 𝑑𝑤2 - 𝑑𝑥2 - 𝑑𝑦2 - 𝑑𝑧2
𝑤2 - 𝑥2 - 𝑦2 - 𝑧2 = 𝑅2,
which shows that the 3-space can be represented as a three-dimensional hyperboloid in the four-dimensional Minkowski space. The hypersurface is defined by the coordinate rnges,
0 ≤ 𝜒 ≤ ∞, 0 ≤ 𝜃 ≤ π, 0 ≤ 𝜙 ≤ 2π
The 2-surfaces 𝜒 = constant are 2-spheres with surface area
𝛢 = 4π𝑅2 sinh2𝜒 '
which increases indefinitely as 𝜒 increases. The proper radius of such a 2-sphere is 𝑅𝜒, and so the surface area is larger than that in Euclidean space. The total volume of the space is infinite.
We can summarize the above discussion as follows
(14.11) 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑅2(𝑡)[𝑑𝜒2 + 𝑆2(𝜒)(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
(14.12) 𝑟 = 𝑆(𝜒) = {sin 𝜒, if 𝑘 = 1, 𝜒, if 𝑘 = 0, sinh 𝜒, if 𝑘 = -1}.
14.8 Geodesics in the FRW metric .
In the comoving coordinate systems the 'cosmological fluid' is at rest and we now consider the motion of particles travelling with respect to the frame. It is free in the sense that it is affected only by the 'background' cosmological gravitatinal field and no other fields. This could be a projectile shot out of a galaxy or a light wave (photon) travelling through intergalactic space.
It is convenient to the express the FRW metric in the form (3.11) and write [𝑥𝜇] = (𝑡, 𝜒, 𝜃, 𝜙], so that
𝑔00 = 𝑐2, 𝑔11 = -𝑅2(𝑡), 𝑔22 = -𝑅2(𝑡)𝑆2(𝜒), 𝑔33 = -𝑅2(𝑡)𝑆2(𝜒) sin2𝜃.
The path of a particle is given by the geodesic equation. (Refer to[Islam 2002 p.46] and [Hobson Efstathiou Lasenby 2006] as follows together!)
𝑑𝑢𝜇/𝑑𝜆 + 𝛤𝜇𝜈𝜎𝑢𝜈𝑢𝜎,
where 𝑢𝜇 = 𝑑𝑥𝜇/𝑑𝜆. For our present purpose it will be more useful to use rewrite the geodesic equation in the form [Hobson Efstathiou Lasenby 2006, p.81]
𝑑𝑢𝜇/𝑑𝜆 = 1/2 𝑔𝜈𝜎,𝜇 𝑢𝜈𝑢𝜎,
which shows if the metric 𝑔𝜈𝜎 is independent of a particular coordinate 𝑥𝜆 then 𝑢𝜆 = constant, i.e. it is conserved along the geodesic.
Let us suppose that the geodesic passes through some spatial point 𝑃 of which 𝜒 = 0 and consider 𝜙-component 𝑢3, 𝜃-component 𝑢2, 𝑟-component 𝑢1 in turn.
For the 𝜙-component, since the metric is independent of 𝜙, we have 𝑑𝜇𝜇/𝑑𝜆 = 0 so that 𝑢3 is constant along the geodesic.
𝑢3 = 𝑔33𝑢3 = -𝑅2(𝑡)𝑆2(𝜒) sin2𝜃 𝑢3
so that 𝑢3 = 0 at the point 𝑃 where 𝜒 = 0, Thus 𝑢3 = 0 along the path and also we have 𝑢3 = 𝑑𝜙/𝑑𝜆 = 0 as well. So 𝜙 is constant along the along the geodesic,
𝜙 = constant.
For the 𝜃-component, we have,
(14.13) 𝑑𝑢2/𝑑𝜆 = -1/2 𝑔𝜈𝜎,2 𝑢𝜈𝑢𝜎 = 0
The only component of 𝑔𝜈𝜎 which depends on 𝑥2 = 𝜃 is 𝑔33 and since 𝑢3 = 0, 𝑑𝑢2/𝑑𝜆 vanishes. So 𝑢2 is constant along the geodesic. Again,
𝑢2 = 𝑔22𝑢2 = -𝑅2(𝑡)𝑆2(𝜒) 𝑢2,
which vanishes at 𝑃(𝜒 = 0), and so 𝑢2 is zero along the geodesic, as 𝑢2, so that
𝜃 = constant.
For the 𝜒-component, we have 𝑢2 = 𝑢3 = 0, while 𝑔00 and 𝑔11 are independent of 𝜒. Thus
(14.14) 𝑑𝑢1/𝑑𝜆 = -1/2 𝑔𝜈𝜎,1 𝑢𝜈𝑢𝜎.
We have 𝑑𝑢1/𝑑𝜆 = 0, so that 𝑢1 is constant along the geodesic. so 𝑢1 = 𝑔11𝑢1 must be constant.Thus we have
(14.15) 𝑅2(𝑡) 𝑑𝜒/𝑑𝑠 = constant.
where we have taken the parameter 𝜆 to be the propertime 𝑠. [Islam 2002 p.47]
Finally, 𝑢0 = 𝑡 can be found from the appropriate normalization condition, because 𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑅2(𝑡)𝑑𝜒2 as above, we have 𝑑𝑠2 = 𝑢𝜇𝑢𝜇 = 𝑐2 for massive particles or 𝑑𝑠2 = 0 for a photon according to Special Relativity [Mukhanov 2005 p.37], then we have
(𝑑𝑡/𝑑𝑠)2 = 1 + [𝑅2(𝑡) (𝑑𝜒/𝑑𝑠)2]/𝑐2 for a massive particle,
(𝑑𝑡/𝑑𝑠)2 = [𝑅2(𝑡) (𝑑𝜒/𝑑𝑠)2]/𝑐2 for a photon.
14.9 The cosmological redshift .
Suppose that a photon is emitted at cosmic time 𝑡𝐸 by a comoving observer with fixed spatial coordinates (𝜒𝐸, 𝜃𝐸, 𝜙𝐸) and received by another observer of (𝑡𝐸, 𝜒𝐸, 𝜃𝐸, 𝜙𝐸). We may take the latter to be at the origin of our spatial coordinate system.
For a photon one can choose an affine parameter such that the 4-momentum is 𝑝𝜇 = 𝑑𝑥𝜇/𝑑𝜆. Since 𝑑𝜃 = 𝑑𝜙 = 0 along the photon geodesic or equivalently 𝑝2 = 𝑝3 = 0 and 𝑝1 is constant along the geodesic and the photon momentum is null, we require 𝑔𝜇𝜈𝑝𝜇𝑝𝜈 = 0, which reduces to
1/𝑐2 (𝑝0)2 - 1/𝑅2(𝑡) (𝑝1)2 = 0,
from which we find 𝑝0 = 𝑐𝑝1/𝑅(𝑡).
According to [Hobson Efstathiou Lasenby 2006 Appendix 9A], for an emitter and recevier with fixed spatial coordinate, the frequency shift of the photon is given, in general, by
(14.16) 𝜈𝑅/𝜈𝐸 = 𝑝0(𝑅)/𝑝0(𝐸) [𝑔00(𝐸)/𝑔00(𝑅)]1/2
For the FRW metric we have 𝑔00 = 𝑐2, and so we find immediately that
(14.17) 1 + 𝑧 ≡ 𝜈𝐸/𝜈𝑅 = 𝑅(𝑡𝑅)/𝑅(𝑡𝐸),
where 𝑧 = (𝜆𝑅 - 𝜆𝐸)/𝜆𝐸 is the fractional change in the wavelength. Thus we see that if the scale factor 𝑅(𝑡) is increasing with cosmic time, so that the universe is expanding, the photon is redshifted by an amount 𝑧 and vice versa.
We may also arrive at this result directly from the FRW metric.Since 𝑑𝑠 = 𝑑𝜃 = 𝑑𝜙 = 0 along the photon path, from (3.11), we have
(14.17a) ∫𝑡𝑅𝑡𝐸𝑐𝑑𝑡/𝑅(𝑡) = ∫𝜒𝐸0𝑑𝜒 = 𝜒𝐸.
Now, if the emmitter sends a second light purse at time 𝑡𝐸 + 𝛿𝑡𝐸, which is received by at time 𝑡𝑅 + 𝛿𝑡𝑅, then
∫𝑡𝑅+𝛿𝑡𝑅𝑡𝐸+𝛿𝑡𝐸𝑐𝑑𝑡/𝑅(𝑡) = ∫𝜒𝐸0𝑑𝜒 = 𝜒𝐸.
from which we see immediatly [Ohanian Ruffini 1994 p.567 Fig. 9.18] that
∫𝑡𝑅+𝛿𝑡𝑅𝑡𝑅𝑐𝑑𝑡/𝑅(𝑡) = ∫𝑡𝐸+𝛿𝑡𝐸𝑡𝐸𝑐𝑑𝑡/𝑅(𝑡)
Asumming 𝛿𝑡𝑅, 𝛿𝑡𝐸 to be small compared to 𝑡𝑅, 𝑡𝐸, the above can be approximately as follows
𝛿𝑡𝑅/𝑅(𝑡𝑅) = 𝛿𝑡𝐸/𝑅(𝑡𝐸)
Considering the pulse to be the successive wavecrests of an electromagnetic wave, we again find that
1 + 𝑧 ≡ 𝜈𝐸/𝜈𝑅 = 𝛿𝑡𝑅/𝛿𝑡𝐸 = 𝑅(𝑡𝑅)/𝑅(𝑡𝐸).
14.10 The Hubble and decceleration parameters .
In a common notation we denote the present cosmic time as 𝑡0. If a nearby galaxy emits a photo at cosmic time 𝑡, we can write 𝑡 = 𝑡0 - 𝛿𝑡, where 𝛿𝑡 ≪ 𝑡0. Let us expand the scale factor 𝑅(𝑡) as a power series about the present epoch 𝑡0 to obtain
(14.18) 𝑅(𝑡) = 𝑅[𝑡0 - (𝑡0 - 𝑡)]
= 𝑅(𝑡0) - (𝑡0 - 𝑡)Ṙ(𝑡0) + 1/2 (𝑡0 - 𝑡)2Ȑ(𝑡0) - ∙∙∙
= 𝑅(𝑡0)[1 - (𝑡0 - 𝑡)𝐻(𝑡0) - 1/2 (𝑡0 - 𝑡)2𝑞(𝑡0)𝐻2(𝑡0) - ∙∙∙ ],
where we have introduced the Hubble parameter 𝐻(𝑡) and the decceleration parameter 𝑞(𝑡). These are given by
(14.19) 𝐻(𝑡) ≡ Ṙ(𝑡)/𝑅(𝑡), 𝑞(𝑡) ≡ - Ȑ(𝑡)𝑅(𝑡)/Ṙ2(𝑡)
where the dot corresponds to differentiation with respect to cosmic time 𝑡. The present-day values of them are usually denoted by 𝐻0 ≡ 𝐻(𝑡0) and 𝑞0 ≡ 𝑞(𝑡0).
𝑧 = 𝑅(𝑡0) /𝑅(𝑡) - 1 = [1 - (𝑡0 - 𝑡)𝐻(𝑡0) - 1/2 (𝑡0 - 𝑡)2𝑞(𝑡0)𝐻2(𝑡0) - ∙∙∙ ]-1 - 1
and assuming that 𝑡0 - 𝑡 ≪ 𝑡0, we have
(14.20) 𝑧 = (𝑡0 - 𝑡)𝐻0 + (𝑡0 - 𝑡)2(1 + 1/2 𝑞0)𝐻02 + ∙∙∙.
(14.21) 𝑡0 - 𝑡 = 𝐻0-1𝑧 - 𝐻0-1(1 + 1/2 𝑞0)𝑧2 + ∙∙∙.
Using the Taylor expansion (3.18), we can also obtain an approximate 𝜒-coordinate of the emitting galaxy from (3.17a),
𝜒 = ∫𝑡0𝑡 𝑐𝑑𝑡/𝑅(𝑡) = ∫𝑡0𝑡𝑐𝑅0-1 [1 - (𝑡0 - 𝑡)𝐻0 - ∙∙∙ ]-1 𝑑𝑡.
Assuming once more that 𝑡0 - 𝑡 ≪ 𝑡0and then using (3.21) again, we have
(14.22) 𝜒 = 𝑐𝑅0-1[(𝑡0 - 𝑡) + 1/2 (𝑡0 - 𝑡)2𝐻0+ ∙∙∙ ].
(14.23) 𝜒 = 𝑐/𝑅0𝐻0[𝑧 - 1/2(1 + 𝑞0)𝑧2 + ∙∙∙ ].
From the FRW metric, we see that the proper distance 𝑑 to the emitting galaxy at 𝑡0 is 𝑑 = 𝑅0𝜒. Thus for very nearby galaxies, 𝑑 ≈ 𝑐(𝑡0 - 𝑡) and 𝑧 ≈ (𝑡0 - 𝑡)𝐻0. So if we interpret the cosmological redshift as a Doppler shift due to a recession velocity 𝑣 of the emitting galaxy, we would obtain
(14.24) 𝑣 = 𝑐𝑧 = 𝐻0𝑑,
which is approximately valid for small 𝑧. This is Hubble's law, named after Edwin Hubble who discovered the expansion of the universe in 1929 by comparing redshifs with distance measurements to nearby galaxies (derived from the period-luminosity relation of Cepheid variables). The quantity 1/𝐻0 gives the age of the universe within a factor of unity. By combining the xpression (14.18) (14.19) and (19.21), we can get
(14.25) 𝐻(𝑧) = 𝐻0[1 + (1 + 𝑞0)𝑧 - ...].
So far, we have been considering the low-𝑧 limit. In general, we have
𝑑𝑧 = 𝑑(1+ 𝑧) = 𝑑(𝑅0/𝑅) = -𝑅0/𝑅2 Ṙ 𝑑𝑡 = -(1+ 𝑧) 𝐻(𝑧) 𝑑𝑡,
where we used quotient rule and get a useful relation between an interval in redshift and the corresponding interval in cosmic time. Thus we can write the look-back time as
(14.26) 𝑡0 - 𝑡 = ∫𝑡0𝑡 𝑑𝑡 = ∫𝑧0 𝑑𝑧/[(1+ 𝑧)𝐻(𝑧)],
and galaxiy's 𝜒-coordinate is given by
(14.27) 𝜒 = ∫𝑡0𝑡 𝑐𝑑𝑡/𝑅(𝑡) = 𝑐/𝑅0 ∫𝑧0 𝑑𝑧/𝐻(𝑧).
In order to evaluate these integrals we must know 𝐻(𝑧) which requires knowledge of the evolution of the scale factor 𝑅(𝑡).
14.11 Distances in the FRW geometry .
Distance measures in an expanding universe can be confusing. What do you mean by the 'distance' to a galaxy? From the FRW metric
𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑅2(𝑡)[𝑑𝜒2 + 𝑆2(𝜒)(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)],
The parameter 𝜒 is sometimes referred to as the coordinate distance, whereas the proper distance to an object at some cosmic time is 𝑑 = 𝑅(𝑡)𝜒, but this cannot be measured in practice. The two most important operationally defined distance measures are the luminosity distance and the angular diameter distance. These distance measures form the basis for observation of the universe.
[Luminosity distance]
In an ordinary static Euclidean universe, if a source of absolute lumnosity 𝐿 (in 𝑊 = 𝐽/𝑠) is a distance 𝑑 then the flux that we received (in 𝑊/𝑚2) is 𝐹 = 𝐿/(4π𝑑2). In the FRW geometry, if we know the luminosity 𝐿 and we observe a flux 𝐹, then the quantity
(14.28) 𝑑𝐿 = (𝐿/4π𝐹)1/2,
is called the luminosity distance of the source. This is an operational definition.
Consider an emitting souce 𝐸 with a fixed comoving coordinate 𝜒 relative to an observer 𝑂 (the emitter would assign the same value of 𝜒 to the observer). We assume that the absolute luminosity of 𝐸 as a function of cosmic time is 𝐿(𝑡) and the photons which have be emitted at an earlier time 𝑡e are detected by 𝑂 at cosmic time 𝑡0. Assuming the photons to have been emitted isotropically, the radiation will be spread evenly over a sphere centered on 𝐸 and passing trough 𝑂 (see Figure 14.2). The proper area of part of the sphere iis
𝛢 = 4π𝑅2(𝑡0)𝑆2(𝜒).
However, each photon received by 𝑂 is redshifted in frequency, so that
𝜈0 = 𝜈e/(1+ 𝑧),
and the arrival rate of the photons is also reduced by the sme factor. Thus, the observed flux at 𝑂 is
𝐹(𝑡0) = 𝐿(𝑡e)/4π[𝑅0𝑆(𝜒)]2 ⨯ 1/(1+ 𝑧)2,
Thus the luminosity distance defined above is now
(14.29) 𝑑𝐿 = 𝑅0𝑆(𝜒)(1+ 𝑧).
[Angular diameter distance]
In Euclidean spaceit were at a distance 𝑑 it would subtend an angular diameter 𝛥𝜃 = 𝐷/𝑑. in an FRW geometry, we thus define the angluar diameter distance to an object to be
(14.30) 𝑑𝐴 = 𝓁/𝛥𝜃.
This is again an operational definition. Suppose we have two radial null geodesics (light path) meeting at the observer at time 𝑡0 with the angular separation 𝛥𝜃, having been emitted at time 𝑡e from a a source of proper diameter 𝓁 at a fixed comoving coordinate 𝜒 (asumming that 𝜙 = constant); see Figure 14.3 and the view of looking it vertically down Figure 14.4. From the FRW metric we have
𝓁 = 𝑅(𝑡e)𝑆(𝜒)𝛥𝜃, 𝑑𝐴 = 𝑅(𝑡e)𝑆(𝜒) = 𝑅(𝑡0) ⨯ 𝑅(𝑡e)/𝑅(𝑡0) ⨯ 𝑆(𝜒) = 𝑅(𝑡0)𝑆(𝜒) /(1+ 𝑧),
(14.31) 𝑑𝐴 = 𝑅(𝑡0)𝑆(𝜒) /(1+ 𝑧),
Of course, we need to know the time history of 𝑅(𝑡) to evaluate 𝑑𝐿 and 𝑑𝐴 because of the 𝜒-dependence.
14.12 Volumes and number densities in the FRW geometry .
The interpretation of cosmological observation often requires one to determine the volume of some three-dimensional region of the FRW geometry. Consider a comoving observer at the origin 𝜒 = 0 and we see that at cosmic time 𝑡0, the proper volume of the region of space lying in the infinitesimal coordinate range 𝜒 → 𝜒 + 𝑑𝜒 and subtending an infinitesimal solid angle 𝑑𝛺 = sin 𝜃 𝑑𝜃 𝑑𝜙 at the observer is
𝑑𝑉0 = (𝑅0 𝑑𝜒)[𝑅02𝑆2(𝜒) 𝑑𝛺] = 𝑅03𝑆2(𝜒) 𝑑𝜒 𝑑𝛺.
For the interval 𝜒 → 𝜒 + 𝑑𝜒 in the radial comoving coordinate there exists a corresponding interval 𝑧 → 𝑧 + 𝑑𝑧 and 𝑡 → 𝑡 + 𝑑𝑡 within which the light observed by 𝑂 at 𝑡 = 𝑡0 was emitted. We may therefore write the volume element as
𝑑𝑉0 = 𝑅03𝑆2(𝜒) (𝑑𝜒/𝑑𝑧) 𝑑𝑧 𝑑𝛺.
From (14.27) we can find the equivalent of 𝑑𝜒/𝑑𝑧 and so
𝑑𝜒/𝑑𝑧 = 𝑐/𝑅0𝐻(𝑧), 𝑑𝑉0 = 𝑐𝑅02𝑆2(𝜒(𝑧))/𝐻(𝑧) 𝑑𝑧 𝑑𝛺,
where we have a function of 𝑧. This volume element is illustrated in Figure 14.5. Finally using (14.17) we have
(14.32) 𝑑𝑉(𝑧) = 𝑑𝑉0/(1+ 𝑧)3 = 𝑐𝑅02𝑆2(𝜒(𝑧))/[(1+ 𝑧)3𝐻(𝑧)] 𝑑𝑧 𝑑𝛺.
The main use of (14.32) is in predicting the numbers of galaxies. Suppose the proper number density of galaxies at a redshift 𝑧 is given by 𝑛(𝑧) and the total number 𝑑𝛮 of such objects is
(14.33) 𝑑𝛮 = 𝑛(𝑧)𝑑𝑉(𝑧) = 𝑐𝑅02𝑆2(𝜒(𝑧))/𝐻(𝑧) 𝑛(𝑧)/(1+ 𝑧)3 𝑑𝑧 𝑑𝛺.
14.13 The cosmological field equation .
The dynamics of spacetime geometry is characterized entirely by the scale factor 𝑅(𝑡), we must solve the gravitational field equations in the presence of matter.
The standard Einstein field equations are
𝑅𝜇𝜈 - 1/2 𝑔𝜇𝜈𝑅 = -𝜅𝑇𝜇𝜈, 𝜅 = 8π𝐺/𝑐4,
where in the right-hand side we may use minus sign for consistency with Newtonian theory. In fact Einstein proposed a modification known as the cosmological term. Because we can add any constant multiple of 𝑔𝜇𝜈 to the left-hand side of the above equation and still obtain a consistent set of field equations. It is usual to denote this multiple by 𝛬. So the field equation become [Hobson Efstathiou Lasenby 2006 p.185]
(14.34) 𝑅𝜇𝜈 = -𝜅(𝑇𝜇𝜈 - 1/2 𝑇𝑔𝜇𝜈) + 𝛬𝑔𝜇𝜈, 𝑇 = 𝑇𝜇𝜇.
For simplicity, we assume a perfect flluid, which is characterized at each point by its proper density 𝜌 and the pressure 𝑝 in the instantaneous rest frame. The energy-momentum tensor is given by [Hobson Efstathiou Lasenby 2006 p.179]
(14.35) 𝑇𝜇𝜈 = (𝜌 + 𝑝/𝑐2)𝑢𝜇𝑢𝜈 - 𝑝𝑔𝜇𝜈.
Since we are seeking solutions for a homogeneous and isotropic universe, the density 𝜌 and the pressure 𝑝 must be funtions of cosmic time t alone.
We may perform the calculation by adopting the comoving coordinates [𝑥𝜇] = (𝑡, 𝑟, 𝜃, 𝜙) in which the FRW metric is from (3.10)
𝑑𝑠2 = 𝑐2𝑑𝑡2 - 𝑅2(𝑡)[𝑑𝑟2/(1 - 𝑘𝑟2) + 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2)].
Thus the covariant components 𝑔𝜇𝜈 of the metric are
𝑔00 = 𝑐2, 𝑔11 = -𝑅2(𝑡)/(1 - 𝑘𝑟2), 𝑔22 = -𝑅2(𝑡)𝑟2, 𝑔33 = -𝑅2(𝑡)𝑟2sin2𝜃.
Since the metric is diagonal, the contravariant components 𝑔𝜇𝜈 are simply the reciprocals of them.
The connection is given in terms of the metric by the following equation and from which we have only non-zero coefficients are
𝛤𝜎𝜇𝜈 = 1/2 𝑔𝜎𝜌(𝑔𝜇𝜈(𝑔𝜌𝜇,𝜈 + 𝑔𝜌𝜈,𝜇 - 𝑔𝜇𝜈,𝜌,
𝛤011 = 𝑅Ṙ/𝑐2(1 - 𝑘𝑟2), 𝛤022 = 𝑅Ṙ𝑟2/𝑐2, 𝛤033 = 𝑅Ṙ𝑟2 sin2𝜃/𝑐2
𝛤101 = Ṙ/𝑅, 𝛤111 = 𝑘𝑟/(1 - 𝑘𝑟2), 𝛤122 = -𝑟(1 - 𝑘𝑟2), 𝛤133 = -𝑟(1 - 𝑘𝑟2) sin2𝜃,
𝛤202 = 𝛤303 = Ṙ/𝑅, 𝛤212 = 𝛤313 = 1/𝑟, 𝛤233 = - sin 𝜃 cos 𝜃, 𝛤323 = cot 𝜃,
where the dot denote differentiation with respect to cosmic time 𝑡. We next substitute these expression for the Ricci tensor,
𝑅𝜇𝜈 = 𝛤𝜎𝜇𝜎,𝜈 - 𝛤𝜎𝜇𝜈,𝜎 + 𝛤𝜌𝜇𝜎𝛤𝜎𝜌𝜈 - 𝛤𝜌𝜇𝜈𝛤𝜎𝜌𝜎.
𝑅00 = 3Ȑ/𝑅, 𝑅11 = -(𝑅Ȑ + 2Ṙ + 2𝑐2𝑘)𝑐-2/(1 - 𝑘𝑟2), 𝑅22 = -(𝑅Ȑ + 2Ṙ + 2𝑐2𝑘)𝑐-2𝑟2, 𝑅33 = -(𝑅Ȑ + 2Ṙ + 2𝑐2𝑘)𝑐-2𝑟2 sin2𝜃,
In our comoving coordinate system (𝑡, 𝑟, 𝜃, 𝜙), the 4-velocity of the fluid simply
[𝑢𝜇] = (1, 0, 0, 0),
which we can write 𝑢𝜇 = 𝛿𝜇0. Thus the covariant components of the 4-velocity and the energy-momentum tensor are
𝑢𝜇 = 𝑔𝜇𝜈𝛿𝜈0 = 𝑔𝜇0 = 𝑐2𝛿0𝜇,
𝑇𝜇𝜈 = (𝜌𝑐2 + 𝑝)𝑐2𝛿0𝜇𝛿0𝜈 - 𝑝𝑔𝜇𝜈.
𝑇 = 𝑇𝜇𝜇 = (𝜌 + 𝑝/𝑐2)𝑐2 - 𝑝 - 𝑝𝛿𝜇𝜇 = 𝑝𝑐2 - 3𝑝.
𝑇𝜇𝜈 - 1/2 𝑇𝑔𝜇𝜈 = (𝜌𝑐2 + 𝑝)𝑐2𝛿0𝜇𝛿0𝜈 - 1/2 (𝑝𝑐2 - 𝑝)𝑔𝜇𝜈.
Including the cosmological-constant term, the field equations (3.24) vanish for 𝜇 ≠ 𝜈. The non-zero components reads
𝑅00 = -𝜅(𝑇00 - 1/2 𝑇𝑔00) + 𝛬𝑔00 = -1/2 𝜅(𝜌𝑐2 + 3𝑝)𝑐2 + 𝛬𝑐2,
𝑅11 = -𝜅(𝑇11 - 1/2 𝑇𝑔11) + 𝛬𝑔11 = -1/2 [𝜅(𝜌𝑐2 - 𝑝) + 𝛬]𝑅2/(1 - 𝑘𝑟2),
𝑅22 = -𝜅(𝑇22 - 1/2 𝑇𝑔22) + 𝛬𝑔22 = -1/2 [𝜅(𝜌𝑐2 - 𝑝) + 𝛬]𝑅2𝑟2,
𝑅33 = -𝜅(𝑇33 - 1/2 𝑇𝑔33) + 𝛬𝑔33 = -1/2 [𝜅(𝜌𝑐2 - 𝑝) + 𝛬]𝑅2𝑟2 sin2𝜃,
Combining these expression with those of Ricci tensor, the field equation yield just the two independent equations
3Ȑ/𝑅 = -1/2 𝜅(𝜌𝑐2 + 3𝑝)𝑐2 + 𝛬𝑐2,
𝑅Ȑ + 2Ṙ + 2𝑐2𝑘 = [1/2 𝜅(𝜌𝑐2 - 𝑝) + 𝛬]𝑐2𝑅2.
Finally, we arrive at the cosmological field equation by eliminating Ȑ from the second equation and remembering 𝜅 = 8π𝐺/𝑐4
Ȑ = -4π𝐺3 (𝜌 + 3𝑝/𝑐2)𝑅 + 1/3 𝛬𝑐2𝑅.
(14.36) Ṙ = -8π𝐺3 𝜌𝑅2 + 1/3 𝛬𝑐2𝑅2 - 𝑐2𝑘.
These two equations are known as the Friedmann-Lemaitre equations. and in the case 𝛬 = 0 they often called the Friedmann equations.
14.14 Equation of motion for the cosmological fluid .
We can derive one more important equation which is often useful in shortening calculations) from the fact that energy-momentum conservation requires [Islam 2002 p.52; with the value adjusted of 𝑇00 because of using 𝑥0 = 𝑐𝑡 instead of 𝑥0 = 𝑡]
𝑇𝜇𝜈;𝜈 = 𝑇𝜇𝜈,𝜈 + 𝛤𝜇𝜈𝜎𝑇𝜎𝜈 + 𝛤𝜈𝜈𝜎𝑇𝜇𝜎 = 0.
𝑇00 = 𝜌𝑐2, 𝑇11 = 𝑝(1 - 𝑘𝑟2)/𝑅2, 𝑇22 = 𝑝/(𝑟2𝑅2), 𝑇33 = 𝑝/(𝑟2 sin2𝜃 𝑅2),
(14.39) ῤ + (𝜌 + 𝑝/𝑐2)3Ṙ/𝑅 = 0.
.
* Textbook: M.P. Hobson, G. Efstathiou and A.N. Lasenby General Relativity An Introduction for Physicists (Cambridge University Press 2006)
※ attention: some rigorous derivation might be required |
|
|