|
김관석
|
2020-05-13 13:44:21, 조회수 : 16,489 |
- Download #1 : 11_c.jpg (140.2 KB), Download : 1

11.9 Kruskal coordinate (Kruskal 좌표)
우리의 advanced 그리고 retarded Eddington-Finkelstein 좌표들의 논의에서, 우리는 어떤 것도 완전히 만족스럽지 않았다는 것을 발견했다. 전자에서
나가는 null 광선들이 불연속적이고, 후자에서는 들어오는 null 광선들이 불연속적이다. 들어오고 나가는 방사상의 photon 측지선들이 연속적인 직선인
그러한 좌표계가 드디어 1961년 Martin Kruskal에 의해서 발견되었고, 또한 이는 완전한 Schwarzschild 기하학의 구조를 밝히는 역할을 한다.
이를 시작하는 한 분명한 방법은 advanced null 좌표 𝑝 와 retarded null 좌표 𝑞 양자 모두를 도입하는 것이다. 좌표 (𝑝, 𝑞, 𝜃, 𝜙)에서 Schwarzschild
metric은 다음이 된다.
𝑑𝑠2 = (1 - 2𝜇/𝑟) 𝑑𝑝 𝑑𝑞 - 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2). (11.16)
여기서 𝑟 은 𝑝 와 𝑞 의 한 함수로 고려되어, 다음에 의해서 간접적으로 정의된다.
1/2 (𝑝 - 𝑞) = 𝑟 + 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣,
우리의 새 좌표계의 어떤 매력적인 성질들 중에서 가장 중요한 것은 𝜃 = constant, 𝜙 = constant에 의해 정의된 2-공간의 단순한 metric이다.
𝑑𝑠2 = (1 - 2𝜇/𝑟) 𝑑𝑝 𝑑𝑞. (11.17)
null 좌표 𝑝 와 𝑞 로부터 새 좌표로 변환하면
𝑐𝑡 = 1/2 (𝑝 + 𝑞), (11.18)
𝑟̄ = 1/2 (𝑝 - 𝑞) = 𝑟 + 2𝜇 ln ∣ 𝑟/2𝜇 - 1 ∣, (11.19)
여기서 𝑡 는 표준 Schwarzschild timelike 좌표이고, 𝑟̄ 는 방사상 spacelike 좌표 (가끔 거북좌표 라고 불린다!), 그러면 2-공간 metric은 다음이 된다.
𝑑𝑠2 = (1 - 2𝜇/𝑟)(𝑐2𝑑𝑡2 - 𝑑𝑟̄ 2) (11.20)
= 𝛺2(𝑥)𝜂𝜇𝜈𝑑𝑥𝜇𝑑𝑥𝜈, (11.21)
여기서 𝑥0 = 𝑐𝑡 또한 𝑥1 = 𝑟̄ 이다. 이 선 요소는 한 Minkowsk 2-공간 (그것은 공간적으로 평평하다) 의 그것과 같은 형식이지만, 위치의 한 함수로서,
수학자들이 한 conformal(共形的) 축적 인자 𝛺2(𝑥)라 부르는 것에 의해서 곱해진다. 2-공간 자체는 굽어져 있다. 왜냐하면 그 함수 𝛺(𝑥)의 도함수는
곡률 tensor의 성분으로 들어가기 때문이다.하지만 2-공간 선 요소 (11.21)은 명백하게 conformally 평평하다. 실제로, 임의의 (유사-)Riemannian
다양체는 conformally 평평하며 (Apendix 11C를 보라), 선 요소가 형태 (11.21)를 취하는 좌표계는 항상 그 안에서 존재한다. 우리는 이렇게 2-공간
(11.17)을 위한 한 좌표계를 발견하는 데 성공했다.
선요소 (11.21)의 형식은 빠르게 움직이는 photon들의 경로(거기서 𝑑𝜃 = 𝑑𝜙 = 0)를 연구하기 위한 한 중요한 결과를 야기한다. 왜냐하면 conformal
인자 𝛺2(𝑥)는 단지 한 축척 조정(scaling)으로, 그것은 광추 구조를 변회시키지 않으며 따라서 그 후자는 Minkowski 공간에서의 그것과 같이 보여야만
한다.이리하여, (𝑐𝑡, 𝑟̄ ) 좌표안의 한 시공간 diagram 안에서 들어오고 나가는 양자들의 방사상 null 측지선은 (11.20)안에서 𝑑𝑠2 = 0 을 설정함으로써
쉽게 알 수 있듯이, 경사도 ∓1인 직선들이다. 이것은 매객변수 𝑝 와 𝑞 를 직접적으로 사용하는 대신에 우리는 (11.17)에 의해서 정의된 2-공간의 명백한
conformal 성질을 보존하는 어떤 좌표 변환을 찾아야만 한다는 것을 제시한다. 이 과정에서 우리는 pathological(病理學的) 행동의 원인인 도발적 인자
1 - 2𝜇/𝑟 를 제거해야 한다. 형식 𝑝(𝑝̄)와 𝑞(𝑞̄)의 한 변환이 이 목표를 성취할 것이란 것은 즉각적인며, 이 경우에, 그 metric은 다음이 된다.
𝑑𝑠2 = (1 - 2𝜇/𝑟) (𝑑𝑝/𝑑𝑝̄) (𝑑𝑞/𝑑𝑞̄) 𝑑𝑝̄ 𝑑𝑞̄,
이것은 (11.17)과 같은 일반적인 형식이다, 함수 𝑝(𝑝̄)와 𝑞(𝑞̄)의 다음과 같은 한 적절한 선택은 선 요소 안의 인자 (1 - 2𝜇/𝑟)를 제거한다. (Kruskal에
의해 제시된 것처럼)
𝑝̄ = exp (𝑝/4𝜇), 𝑞̄ = -exp (-𝑞/4𝜇),
그러면 우리는 다음을 발견한다.
𝑑𝑠2 = 32𝜇3/𝑟 exp(-𝑟/2𝜇) 𝑑𝑝̄ 𝑑𝑞̄,
그러면 그 metric의 보통의 형식은 다음으로써 한 timelike 변수 𝑢 와 한 spacelike 변수 𝑣 를 정의함으로써 얻는다.
𝑣 = 1/2 (𝑝̄ + 𝑞̄), 𝑢 = 1/2 (𝑝̄ - 𝑞̄).
이리하여, Kruska 좌표들 (𝑢, 𝑣, 𝜃, 𝜙)로 Schwarzschild 기하학을 위한 완전한 선 요소는 다음으로 주어진다.
𝑑𝑠2 = 32𝜇3/𝑟 exp(-𝑟/2𝜇) (𝑑𝑣2 - 𝑑𝑢2) - 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2), (11.22)
여기서 𝑟 은 𝑢 와 𝑣 의 한 함수로 고려되고 다음에 의해 간접적으로 정의된다.
𝑢2 - 𝑣2 = (𝑟/2𝜇 - 1) exp(𝑟/2𝜇). (11.23)
다음 변환에 의해서 앞의 𝑢 와 𝑣 가 원래 Schwarzschild 좌표들 𝑡 와 𝑟 로 연관됨을 보여주는 것은 자명하다. 𝑟 > 2𝜇 에서는 우리는 다음을 갖는다.
𝑣 = (𝑟/2𝜇 - 1)1/2 exp(𝑟/4𝜇) sinh(𝑐𝑡/4𝜇), 𝑢 = (𝑟/2𝜇 - 1)1/2 exp(𝑟/4𝜇) cosh(𝑐𝑡/4𝜇),
한편 𝑟 < 2𝜇 에서는,
𝑣 = (𝑟/2𝜇 - 1)1/2 exp(𝑟/4𝜇) cosh(𝑐𝑡/4𝜇), 𝑢 = (𝑟/2𝜇 - 1)1/2 exp(𝑟/4𝜇) sinh(𝑐𝑡/4𝜇).
방사적인 광선들에 의해 정의된 인과적인 구조는 특별하게 (구성적으로) Kruskal 좌표들로 분석하는 것이 용이하다. 그 metric (11.22)로부터 우리는
𝑑𝑠 = 𝑑𝜃 = 𝑑𝜙 = 0 를 위해서 다음을 갖는다.
𝑣 = ∓𝑢 + constant,
그것은 그 축들에 ∓45∘인 직선들을 나타낸다. 이것은 𝑑𝑠 = 𝑑𝜃 = 𝑑𝜙 = 0 인 2-공간은 (𝑢, 𝑣)좌표들에서 분명히 conformally 평평하다는 것을 사실의 한
직접적인 결과이다. 이리하여, 그 광추 구조는 Minkowski 공간 내의 그것처럼 보여야 마땅하다. 또한, 우리는 한 massive한 입자 세계선은 각 점에서
미래 광추의 내부에 항상 반드시 위치한다는 것도 주목한다.
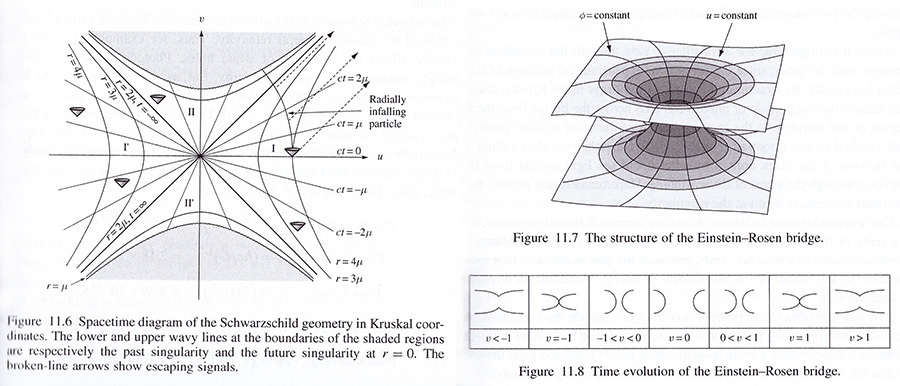
상수 𝑡 와 𝑟 의 선들을 plot하는 것 역시 교육적하다. (11.23)으로부터 우리는 상수 𝑟 의 선들이 상수 𝑢2 - 𝑣2 의 곡선들이고 또한 그래서 쌍곡선이라는
것을 Figure 11.6에서 본다. 특히, 𝑟 = 2𝜇 는 직선 𝑢 = ∓𝑣 이고, 𝑟 = 0 는 양선으로 그려진 쌍곡선 𝑣 = √ (𝑢2 + 1) 이다. 그러나 이는 그 특이점이므로
잘 정의된 dimensionality(차원성)은 아니다. 유사하게 상수 𝑡 도 map화 될 수 있다. 다음을 보여주는 것은 자명하다.
tanh (𝑐𝑡/4𝜇) = {𝑣/𝑢 for 𝑟 > 2𝜇, 𝑢/𝑣 for 𝑟 < 2𝜇},
이들은 원점을 통과하는 직선들이고 Figure 11.6에서 보는 것처럼 𝑡 = -∞ 는 𝑢 =-𝑣 에 해당하고, 𝑡 = ∞ 는 𝑢 =𝑣 에 해당한다. 또한 𝑟 > 2𝜇 를 위한
𝑡 = 0 은 𝑣 = 0에 해당하고, 𝑟 < 2𝜇 를 위한 𝑡 = 0 은 𝑢 = 0에 해당한다.
우리는 Figure 11.6 안의 지역 𝐈 과 𝐈𝐈 로 Schwarzschild 좌표들 -∞ < 𝑡 < ∞, 0 < 𝑟 < ∞ 에 의해서 cover된 전 지역이 map화 되었음을 주목한다.
이렇게 우리는 전 Schwarzschild 기하학을 cover하기 위해서는 두 Schwarzschild 좌표 patch들인 (𝐈, 𝐈𝐈)과 (𝐈', 𝐈𝐈')를 필요로 하지만, 한 단일 Kruskal
좌표계이면 충분하다. 대각선들 𝑟 = 2𝜇, 𝑡 = ∞ 와 𝑟 = 2𝜇, 𝑡 = -∞ 이 시공간 𝐈 과 𝐈𝐈 를 다른 지역 𝐈' 과 𝐈𝐈' 로부터 구분하는 사건 지평선들을 정의한다.
Kruskul diagram은 다소의 기묘한 특징들을 갖는다. 두 'Minkowski' 지역들 𝐈 과 𝐈' 들이 있고, 그래서 분명히 두 우주들이 있다. 우리는 지역 𝐈 을 어떤
Schwarzschild 블랙홀 밖 시공간 지역으로 그리고 지역 𝐈𝐈 를 블랙홀 사건 지평선의 interior와 동일시한다. 지역 𝐈' 과 𝐈𝐈' 는 지역 𝐈 과 𝐈𝐈 로부터 완전히
접근 불가이다. 그 두 우주 𝐈 과 𝐈' 는 실제로 그 원점에서 웜홀 로 연결되지만, 나중에 보여주듯이, 어떤 입자들도 지역 𝐈 과 𝐈' 사이를 여행할 수는 없다.
어떻게 몇개의 단순한 변환이 명백히 새 물리학인 것으로 인도했을까? 우리가 한 것은 Schwarzschild 해를 수학적으로 연장하기 위한 것에 상당한다.
수학자들은 이것을 Schwarzschild 해의 한 극대의 연장 이라고 부르겠다. 왜냐하면 모든 측지선이 그 affine 매개변수의 무한 값까지 연장되거나 과거나
미래의 특이점에서 끝나기 때문이다. 그래서, 우리는 완전한 Schwarzschild 기하학이 한 블랙홀과 화이트홀 그리고 한 웜홀에 의해서 그들 지평선에서
연결된 두 우주들로 구성됨을 발견한다.
고전적 일반상대성은 화이트홀의 존재를 허용한다. 그러나, 당신이 Kruskal diagram에서 볼 수 있듯이, 당신은 오직 과거에 존재하는 화이트홀 '속으로
떨어짛' 수 없다. 우리는 화이트홀이 존재하는 지 확신할 수 없다. 고전적 GR은 특이점에서 붕괴됨에 틀림없다. 우리는 양자 효과가 ultra-short 거리들과
ultra-high energy들에서 중요해진다고 기대할 수 있겠다. 실제, 우리는 세 기본상수 𝐺, ħ 와 𝑐 로부터 다음의 energy, 질량, 시간, 길이와 밀도 축척들을
형성할 수 있다:
Plank energy 𝐸p = (ħ𝑐5/𝐺)1/2 = 1.22 ⨯ 1019GeV,
Plank mass 𝑚p = (ħ𝑐/𝐺)1/2 = 2.18 ⨯ 10-5g,
Plank time 𝑡p = (ħ𝐺/𝑐5)1/2 = 5.39 ⨯ 10-44s,
Plank length 𝑙p = (ħ𝐺/𝑐3)1/2 = 1.62 ⨯ 10-33cm,
Plank density 𝜌p = (𝑐5/ħ𝐺2) = 5.16 ⨯ 1093gcm3.
이 Plank scale들은 양자 중력 효과가 중요하게 되기를 기대하는 곳에서의 특성화된 energy들, 길이들, 시간들 등을 정의한다. Plank 질량의 한 입자는
작은 박테리아 한마리와 거의 같다.
아무도 실제로 블랙홀들의 중심이 참 특이점들에 정박하고 있다고 예상하지는 않는다. 과연, 고전적 특이점에 가까운 양자 중력 효과가 일어날 것이고
고전적 상대성의 발산을 억제할 것이라고 기대된다. 많은 사람들은 M-이론(앞서 초끈으로 알려졌던)이 언제간 그런 이론을 제공할 것이라고 희망하고
있지만, 우리는 한 완전한 양자 중력론을 갖고 있지 않다. 이론가들은 완전한 양자 중력론의 특성을 포함한 (혹은 아닌) 준고전적 이론들을 개발해 왔다.
그런 계산들은 화이트홀은 불안정해서 한 Plank 시간 이상 동안 존재하지 않을 것이라고 제안한다. 다음의 내용들은 기존 물리학의 최첨단 내용이다.
11.10 Wormholes and the Einstein-Rosen 다리 (웜홀과 Einstein-Rosen 다리)
Figure 11.6 에서는 명확하지 않지만, 두 우주 𝐈 과 𝐈' 는 원점에서 실제로는 한 웜홀 로 연결된다. 원점에서의 구조를 이해하려면 당신은 좌표 𝜃 와 𝜙 가
이 도해에서 은폐되었음을 깨달아야만 한다; Figure 11.6 안의 각 점은 실제로 한 2-공간을 나타낸다.
우리는 𝑢 = +∞ 에서 𝑢 = -∞ 까지 달하는 spacelike hypersuface(超曲面) 𝑣 = 0 의 기하학을 고려해서 웜홀로의 다소 직관적 통찰을 얻을 수 있다.
이 hypersurface를 위한 선 요소는
𝑑𝑠2 = -32𝜇3/𝑟 exp(-𝑟/2𝜇) 𝑑𝑢2 - 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙2).
우리는 적도면 𝜃 = π/2 에 해당하는 선 요소가 다음으로 줄어든 이 hypersurface의 한 단면을 그릴 수 있다.
𝑑𝑠2 = -32𝜇3/𝑟 exp(-𝑟/2𝜇) 𝑑𝑢2 - 𝑟2 𝑑𝜙2. (11.24)
이를 해석하기 위해, 우리는 minus (11.24)로 주어진 선요소 𝑑𝜎2 를 소유하고 또한 한 3차원 Euclid 공간에 매입된 2차원적 surface를 고려할 수 있다.
이 매입은, 다음의 친숙한 형태를 나타내도록 보여주는, 𝑑𝜎2 를 좌표 𝑟 과 𝜙 의 용어로 재표현함으로써 가장 쉽게 행할 수 있다.
𝑑𝜎2 = (1 - 2𝜇/𝑟)-1 𝑑𝑟2 + 𝑟2 𝑑𝜙2. (11.25)
그렇지만, 우리는 spacelike hypersurface 𝑣 = 0 안에서는 우리가 𝑢-축을 따라 +∞ 로부터 -∞ 까지 움직이면서 그 𝑟 의 값은 최소값 𝑟 = 2𝜇 (at 𝑢 = 0)
로 감소하고 그리고 다시 증가한다는 것을 반드시 기억해야 한다. 일반적으로, Euclid 공간에서는, 임의 좌표 (𝜉, 𝜂) 로 매개화된 한 2-surface는 삼차원
Euclid 공간에서 어떤 좌표계를 정의하는 𝑥𝑎 를 갖는 세 함수 𝑥𝑎(𝜉, 𝜂)(𝑎 = 1, 2, 3) 을 부여함으로써 명기될 수 있다. 우리의 특별한 경우에서, 삼차원
공간의 선 요소가 다음인, 원통극좌표 (𝜌, 𝜓, 𝑧)를 사용하는 것이 편리할 것이다.
𝑑𝜎2 = 𝑑𝜌2 + 𝜌2𝑑𝜓2 + 𝑑𝑧2. (11.26)
나아가, 우리가 매입을 원하는 2-surface (좌표 𝑟 과 𝜙 로 매개화한)는 명백히 축대칭이며, 다음으로써 이 surface를 명기하는 세 함수를 취할 수 있다.
𝜌 =𝜌(𝑟), 𝜓 = 𝜙, 𝑧 = 𝑧(𝑟).
𝑑𝜎2 = [(𝑑𝜌/𝑑𝑟)2 + (𝑑𝑧/𝑑𝑟)2]𝑑𝑟2 + 𝜌2𝑑𝜙2. (11.27)
이것은 (11.25)와 동일해야 하고, 그래서 우리는𝜌(𝑟) = 𝑟 를 필요로하며, 이리하여
1 + (𝑑𝑧/𝑑𝑟)2 = (1 - 2𝜇/𝑟)-1.
𝑧(𝑟) = √[8𝜇(𝑟 - 2𝜇)] + constant.
상수를 영으로 하고, 𝑟 은 2𝜇 보다 결코 작지 않다는 것을 기억하면, 우리는 Figure 11.7 에서 보이는 형태를 발견한다. 그래서, 𝑣 = 0 에서 spacelike
hypersurface의 기하학은 한 Einstein-Rosen 다리 에 의해 '목구멍(throat)' 𝑟 = 2𝜇 에서 연결된, 두개의 구별되어 있으나 동일하고 점근적으로 평평한
Schwarzschild 다양체로 생각될 수 있다. 만일 그렇기를 바란다면, 목구멍으로부터 먼 한 구역에서 점근적으로 평평한 두 지역을 함께 연결할 수 있다.
이 경우에 그 웜홀은 한 단일 우주에 두 먼 지역들을 연결한다.
어느 경우에서나, 웜홀의 구조는 동적 이다. 사람들은 Schwarzschild 기하학이 '정적'이라 생각하곤 한다. 전통적인 Schwarzschild 좌표들의 용어로
작동하는 것은 𝑡 가 timelike이고 metric 계수들이 𝑡 로부터 독립적이어서 시공간이 정적임을 의미하는 지역 𝐈 과 𝐈' 내에서 뿐이다. 지역 𝐈𝐈 와 𝐈𝐈' 내에서
𝑡-좌표는 spacelike이고, 𝑟-좌표가 timelike이다. 그 metric 계수들이 외연적으로 𝑟 에 의존하는 까닭에 이 지역에서의 시공간은 더 이상 정적이지 않고
이 timelike 좌표에 따라 전개한다. Kruskal 좌표로 돌아가 spacelike hypersurface 𝑣 = 0 를 고려하라. 이 surface가 시간에서 앞으로 나가면 (Kruskal
diagram에서 +𝑣 으로) 그 부분은 지역 𝐈𝐈 로 들어가서 전개하기 시작한다.
𝑣 가 증가하면 hyperspace 기하학의 그림은 정성적으로는 Figure 11.7 과 같지만 그 다리는 좁아지고 그 우주들은 이제는 𝑟 < 2𝜇 에서 결합한다.
𝑣 = 1 에서는 그 다리는 끊어져서 두 우주들은 단순이 특이점 𝑟 = 0 에서 닿아있을 뿐이다. 더 큰 값에서는 두 우주는 𝑟 = 0 에서 특이점을 포함하면서
완전히 분리된다. Kruskal 해가 𝑣 에서 대칭이므로 𝑣 의 음의 값에서도 같은 것이 발생한다. 전체 시간의 전개는 Figure 11.8에서 도식적으로 보여진다.
이렇게 그 두 우주는 각각 무한 곡률의 한 특이점을 (𝑟 = 0) 갖고서, 처음에는 분리되어 있다. 그것들은 시간이 지나면 전개하여, 그들의 특이점은 서로
합쳐져서 한 비특이적인 다리를 형성한다. 그 다리는 𝑣 = 0 에서 그 목구멍에서의 최대 반경 𝑟 = 2𝜇 값에 도달할 때까지 확장한다. 그것은 다음에 축소
하고 끊어져서, 다시 한번 특이점들을 (𝑟 = 0) 포함한 채로 두 우주가 분리되어진다. .
슬프게도, 한 여행자는 한 우주로부터 다른 우주로 건너갈 수가 없다, 왜냐하면, 그 다리의 형성고 확장 그리고 붕괴가 너무나 빨리 일어나기 때문이다,
Kruscal diagram에서 광선의 경로를 검토함으로써 우리는 어떠한 입자나 photon도 한 우주의 먼 지역에서 다른 우주의 먼 지역으로 건너갈 수 없음을
추론할 수 있다. 그럼에도 불구하고, 그 블랙홀의 지평선을 통해 떨어진 후 한 여행자는 웜홀의 목구멍을 통해서 다른 우주로부터의 빛 신호들을 볼 수도
있었다. 불행하게도, 다른 우주를 본 벌은 특이점에서의 죽음이다.
대자연에 웜홀들이 존재할 수 있을까? 그것들이 다른 우주 또는 같은 우주의 다른 부분으로 연결할 수 있을까? 또다시, 아무도 확신할 수는 없다. 많은
이론가들은 웜홀를 이해하기 위해서는 양자 중력을 이해할 필요가 있다고 주장한다. 웜홀들은 아마도 불안정할 것이지만 '실재인' 웜홀들은 양자 중력의
일부분의 공식화(formulation)들에서의 한 특징이다.
11.11 Hawking effect (Hawking 효과)
이제까지 블랙홀의 논의는 순전히 고전적이었다. 1974년 Stephen Hawking은 양자역학의 원리를 한 블랙홀에 가까운 전자기장에 적용을 해서 블랙홀은
그들의 질량에 반비례하는 한 온도를 갖는 한 흑체(blackbody)로서 (그 복사를) 계속 방출한다는 놀라운 결과를 발견했다! Hawking의 원래 계산은 양자
장이론의 기술을 사용하지만 우리는 초보적 논의로부터 아주 단순하게 그 주요한 결과를 유도할 수 있다.
양자 이론에 의하면, 빈 공간의 진공조차도 양자 요동을 나타내어, 여기서 어떤 다른 사건에서 서로 소멸하게 될 뿐인, 입자-반입자 쌍들이 한 사건에서
생성된다. 쌍생성은 energy 보존을 위반하고 그래서 고전적으로는 금지된다. 그렇지만, 양자역학에서는 Heisenberg의 불확정성 원리의 하나의 형식이
𝛥𝑡𝛥𝐸 = ħ 이고, 여기서 𝛥𝐸은 한 시간 𝛥𝑡 동안 한 양자역학적 상태로 거주하는 한 입자의 energy에서 최소 불확정성이다. 이리하여, 그 쌍이 𝛥𝑡 = ħ/𝛥𝐸
보다 짧은 시간에 그 쌍이 소멸한다고 가정하면, 여기서 𝛥𝐸 는 energy 위반의 양이고, 어떤 물리 법칙도 깨지지 않았다.
우리는 이제 그러한 과정이 한 블랙홀의 사건 지평선의 바로 밖에서 일어난다고 고려하도록 한다. 한 입자-반입자 쌍이 진공으로부터 생성되고 그 쌍의
구성들은 4-운동량 𝑝 와 𝑝̄ 를 각각 갖는다고 가정하라. 그 시공간이 고정적이므로 (∂0𝑔𝜇𝜈 = 0), 그 양 𝑝0 = 𝑒0 ⋅ 𝑝 그리고 𝑝̄0 = 𝑒0 ⋅ 𝑝̄ 는 그 입자 세계선을
따라서 보존된다: 여기서 𝑒0 는 𝑡-좌표 기저 vector이다. 이리하여, 그 진공의 한 요동을 위해서 고전적 보존은 다음을 필요로 한다.
𝑒0 ⋅ 𝑝 + 𝑒0 ⋅ 𝑝̄ = 0. (11.28)
그 좌표 기저 vector 𝑒0의 제곱인 '길이'는 다음에 의해서 주어진다.
𝑒0 ⋅ 𝑒0 = 𝑐2(1 - 2𝜇/𝑟 ). (11.29)
이렇게, 그 지평선 (𝑟 > 2𝜇) 밖에서, 𝑒0 는 timelike 이다. 따라서 𝑒0-방향에 따르는 4-속도의 한 관찰자에 의해 측정된 입자 energy는 양임에 틀림없다.
따라서 보존 조건 (11.28)은 만족될 수 없다.
하지만, 만일 그 요동이 그 사건 지평선과 가까운 곳에서 일어난다면, 안으로 향하는 입자는 지역 (𝑟 < 2𝜇) 로 여행할 수 있다. 그 사건 지평선 안에서,
(11.29)에서 보여지듯이, 𝑒0 는 spacelike 이다, 이리하여 𝑒0 ⋅ 𝑝 는 어떤 관찰자를 위한 공간적 운동량 의 한 성분이고, 그래서 음일 수 있다. 그래서,
만일, 그 반입자 (가령) 그 지평선을 음의 𝑒0 ⋅ 𝑝̄ 와 더불어서 넘어가고, 그 입자는 양의 𝑒0 ⋅ 𝑝 과 더불어 무한으로 탈출한다면, 그 보존 조건 (11.28)은
만족될 수 있다. 무한대에 있는 관찰자에 의해서 보여지듯이, 그 블랙홀이 energy 𝑒0 ⋅ 𝑝 의 한 입자를 방출했고, 그 안으로 떨어진 반입자의 결과로서,
블랙홀의 질량이 (𝑒0 ⋅ 𝑝̄)𝑐2 만큼 감소했다. 이것이 Hawking 효과 이다. 물론, 만일 블랙홀 안으로 떨어진 것이 입자이고 무한으로 탈출한 것이 반입자라
하더라도 그 논의는 역시 유효하다. 그 블랙홀은 같은 숫자로 입자들과 반입자들을 방출한다.
그 원거리 관찰자는 입자들과 반입자들의 한 안정된 flux를 본다. 그 flux는 그 기하학이 𝑡 로부터 독립적이고 따라서 입자의 방출 비율 또한 𝑡 로부터
독립적이므로, 안정적임에 틀림없다. 우리는 원거리 관찰자에 의해서 측정된 그러한 한 입자의 전형적인 energy를 계산하도록 한다. 입자-반입자 쌍이
좌표 반경 𝑅 = 2𝜇 + 𝜖인 어떤 사건 𝑃에서 생성되었다고 가정하라. 우리는 이 점에서 정지했다가 출발한 한 자유 낙하하는 한 관찰자에 의해서 그 사건이
보여진다고 고려한다. 그 관찰자는 자유 낙하하고 있으므로, 그의 frame에서는 특수상대성의 규칙이 적용된다. 그 관찰자가 그 지평선에 도달하기 전에
지연된 고유시간 𝛥𝜏 의 한 전형적인 측정은 𝑟 = 𝑅 에서 정지했다 출발한 방사상으로 자유 낙하하는 입자를 고려함으로써 얻어질 수 있다. 이 경우에는,
ṫ = (1 - 2𝜇/𝑅)1/2)/ (1- 2𝜇/𝑟)1/2),
ṙ = [2𝜇𝑐2(1/𝑟 - 1/𝑅)]1/2.
그래서 필료한 고유시간 간격은
𝛥𝜏 = ∫2𝜇2𝜇+𝜖[2𝜇𝑐2/𝑟 - 2𝜇𝑐2/(2𝜇𝑐 + 𝜖)]-1/2 𝑑𝑟 ≈ 2(2𝜇𝜖)1/2/𝑐,
여기서 최종 결과는 𝜖 의 일차식으로 인용된다. 불확실성의 원리로부터, 자유 낙하하는 관찰자에 의해 측정된 그 입자의 전형적 energy 𝓔 는 다음으로써
주어진다.
𝓔 = ħ/𝛥𝜏 = ħ𝑐/2(2𝜇𝜖)1/2
그렇지만, 어것은 또한 다음처럼 쓰여질 수 있다.
𝓔 = 𝑝 ⋅ 𝑢 ≈ 𝑝0𝑢0
여기서 𝑢 는 그 관찰자의 4-속도이고 또한 𝑢0 ≪ 𝑢1 이므로 이 근사식이 유효하다. 이제, 𝜖 의 일차식으로 𝑢0 = ṫ ≈ (1- 2𝜇/𝑟)1/2 이다. 나아가, 𝑝0 는
그 입자의 세계선을 따라서 보존되고, 또한 4-속도가 단순히 [𝑢𝑢] = (1, 0, 0, 0) 인 원거리 관찰자에 의해서 측정된 그 입자의 energy 𝐸 와 일치한다.
이리하여, 우리는 드디어 다음을 얻는다.
𝐸 = 𝓔(𝜖/2𝜇)1/2 = ħ𝑐/4𝐺𝑀, (11.30)
괄목할만하게, 이 결과는 𝜖 에 의존하지 않는다; 그 입자는 항상 이 characteristic(特性化) energy와 더불어 나타난다.
𝑇 = ħ𝑐3/8π𝑘B𝐺𝑀,
완전한 양자 장이론 계산은 그 입자들이 실제로 다음의 Hwaking 온도에 의해 특성화된 한 흑체 enegy spectrum을 받음을 보여준다.
이리하여 전형적 입자 energy는, 우리가 개략 추정한 (11.30)보다 2π 적은 한 인자일 뿐인, 𝐸 = 𝑘B𝑇 = ħ𝑐3/8π𝑘B𝐺𝑀 이다. 이에 수치를 넣으면, 우리는
다음을 발견한다.
𝑇 = 6 ⨯10-8(𝑀/𝑀⊙)-1𝐊.
이리하여 한 태양 질량의 블랙홀로부터의 복사는, 한 대질량인 별의 중력의 붕괴에 의해서 형성될 수 있는 것처럼, 무시할 정도로 작다.
블랙홀이, 고유시간이 𝑡 인 한 고정된 원거리 관찰자에 의해서 결정되면서, 질량을 잃는 비율 𝑑𝑀/𝑑𝑡 를 계산하기는 자명하다. 왜냐하면 블랙홀 사건
지평선은 온도 𝑇 의 한 흑체로서 복사를 방출하기 때문에, 그 블랙홀 질량은 다음의 비율로 감소함에 틀림없다.
𝑑𝑀/𝑑𝑡 = 𝜎𝑇4𝛢/𝑐2,
여기서 𝜎 = π2𝑘B4/60ħ3𝑐2 는 Stefen-Bolzmann 상수이며, 𝛢 는 사건 지평선의 고유 면적이다. Schwarzschild metric으로부터 우리는 𝛢 = 16π𝜇2
임을 발견하고, 그래서 우리는 다음을 얻는다.
𝑑𝑀/𝑑𝑡 = 𝛼ħ/𝑀2, (11.31)
여기서 𝛼 = 𝑐4/15360π𝐺2 = 3.76 ⨯ 1049kg2m-2. (11.31)에 대한 해 𝑀(𝑡) 는 쉽게 계산된다. 시간 𝑡0 에서 그 증발이 완료되는 한 블랙홀을 위해서,
우리는 다음을 발견한다.
𝑀(𝑡) = [3𝛼ħ(𝑡0 - 𝑡)]1/3. (11.32)
이 결과는 한 블랙홀의 생애의 끝에는 곧바로 energy의 한 폭발(burst)이 방출됨을 보여준다. 예를 들면, 마지막 초에 그것은 ∼1022J 의 energy를 주로
𝛾-광선으로 방출해야 마땅하다. 그러한 사건들은 아직까지는 (전혀) 확인되지는 않았다. *
* 'Hawking 복사'는 2019년 5/29 이스라엘의 Jeff Steinhauer가 마침내 학계의 인정을 받으며 이를 증명했음! ⟹ 'Nature'
p.s. Stephen Hawking의 유명한 '시간의 역사'에서 도해로 볼 수 있었던 웜홀이 여기에 수식으로 나오니 신기했음.
'Einstein-Rosen 다리'는 Ludwig Flamm이 1916년에 발견했고, Einstein과 Nathan Rosen이 1935년에 재발견한 이론임.
이 글을 마지막으로, 앞으로 계속할 '현대 우주론'은 세계적 추세에 따라서 공용어-영어로 학습함!
|
|
|





































