|
김관석
|
2020-06-07 16:21:08, 조회수 : 450 |
- Download #1 : F15b.jpg (245.2 KB), Download : 1
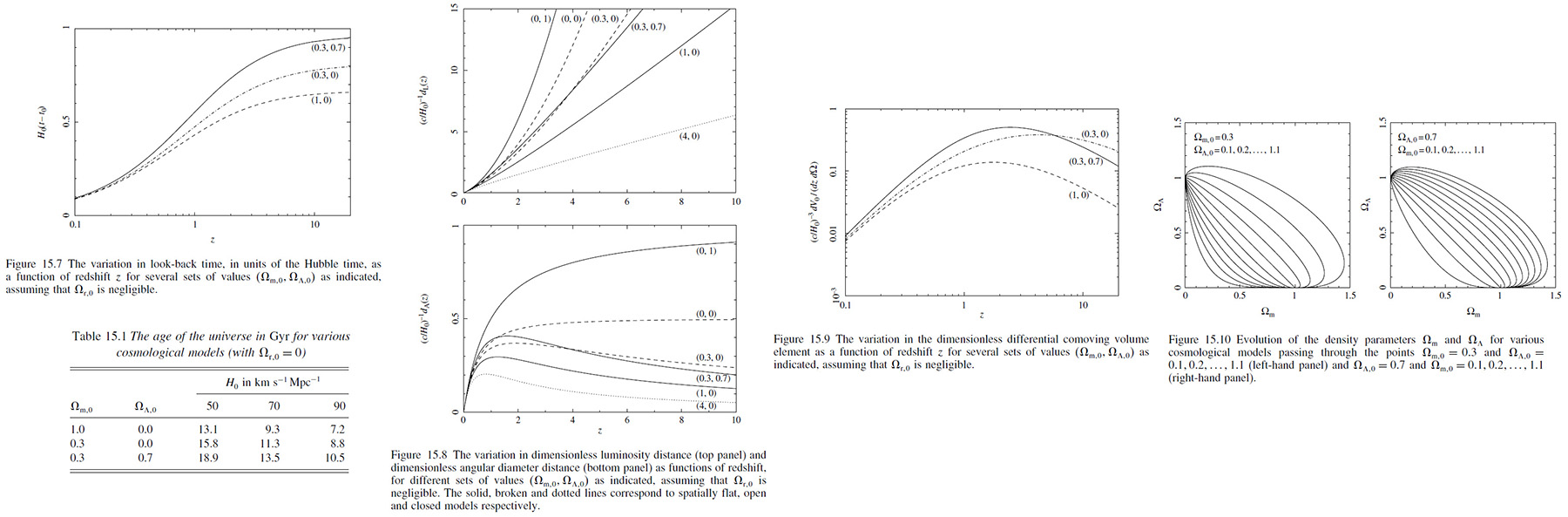

15.7 Look-back time and the age of the universe .
In this section using the four present-day cosmological parameters 𝐻0, 𝛺𝑚,0, 𝛺𝑟,0 and 𝛺𝛬,0 we consider the look-back time and the age of the universe.
Remembering (14.26) of Chapter 14, if a comoving galaxy emmited a photon at cosmic time 𝑡, 'look-back time' 𝑡0 - 𝑡 is given as a function of the photon's redshift by
(15.37) 𝑡0 - 𝑡 = ∫𝑡𝑡0 𝑑𝑡 = ∫0𝑧 𝑑𝑧/[(1 + 𝑧)𝐻(𝑧)].
From the cosmological field equation (15.13), on noting that 𝑎 = 𝑅/𝑅0 = (1 + 𝑧)-1 we obtain the useful result
(15.38) 𝐻2(𝑧) = 𝐻02[𝛺𝑚,0 (1 + 𝑧)3 + 𝛺𝑟,0 (1 + 𝑧)4 + 𝛺𝛬 + 𝛺𝑘,0 (1 + 𝑧)2].
𝑡0 - 𝑡 = 1/𝐻0 ∫0𝑧 𝑑𝑧/[(1 + 𝑧)√{𝛺𝑚,0 (1 + 𝑧)3 + 𝛺𝑟,0 (1 + 𝑧)4 + 𝛺𝛬 + 𝛺𝑘,0 (1 + 𝑧)2}].
A more convenient integral is obtained by substituting 𝑥 = (1 + 𝑧)-1 and we have
(15.39) 𝑡0 - 𝑡 = 1/𝐻0 ∫1(1 + 𝑧)-1 𝑥/√(𝛺𝑚,0𝑥 + 𝛺𝑟,0 + 𝛺𝛬𝑥4 + 𝛺𝑘,0𝑥2) 𝑑𝑥.
Assuming 𝛺𝑟,0 = 0 reasonably, in Figure 15.17 we see 𝐻0(𝑡 - 𝑡0), the look-back time in units of the Hubble time, as a function of redshift for several values of 𝛺𝑚,0 and 𝛺𝛬.
In cosmological model, the age of the universe, i.e. the cosmic time interval between the point of 𝑎(𝑡) = 0 and the present epoch 𝑡 = 𝑡0. Since 𝑧 → ∞ at the big bang, we may obtain an expression of the age of the universe by letting 𝑧 → ∞ in (15.39), so that the lower limit of the integral equals zero. So we can write
𝑡0 = 1/𝐻0 𝑓(𝛺𝑚,0, 𝛺𝑟,0, 𝛺𝛬,0),
where 𝑓 is the value of the integral, which is typically a number of order unity. But it is not possible to perform the integral analytically and so one has to resort to numerical integration. Table 15.1* lists the age of the universe 𝑡0 for the same values as considered in Figure 15.7. It is interesting to compare these values with estimates of the ages of the oldest stars in globular clusters,
𝑡stars ≈ 11.5 ∓ 1.3 Gyr.
Clearly, one requires 𝑡0 > 𝑡stars for a viable cosmology!
Simply by setting 𝑡 = 𝑡0 and 𝑎 = 1, we can obtain the age of the universe for each model with big-bang origin. Foe example. from (15.28) it is 𝑡0 = 2/(3𝐻0) and from the (15.36) in case of 𝛺𝛬,0) > 0 is given by
𝑡0 = 2/(3𝐻0)√𝛺𝛬,0) sinh-1 √[𝛺𝛬,0/(1 - 𝛺𝛬,0)] = 2/3𝐻0 (tanh-1√𝛺𝛬,0)/√𝛺𝛬,0.
15.8 The distance-redshift relation .
We may also obtain a general expression for the comoving 𝜒-coordinate of a galaxy emitting a photon at time 𝑡 that is recieved at time 𝑡0 with redshift 𝑧. This is given by from (14.27)
𝜒 = ∫𝑡𝑡0 𝑐𝑑𝑡/𝑅(𝑡) = 𝑐/𝑅0 ∫0𝑧 𝑑𝑧/𝐻(𝑧).
We may substitute for 𝐻(𝑧) using the expression (15.38). Thus the 𝜒-coordinate of a comoving object with redshift is given by
(15.40) 𝜒(𝑧) = 𝑐/𝑅0𝐻0 ∫0𝑧 𝑑𝑧/√{𝛺𝑚,0 (1 + 𝑧)3 + 𝛺𝑟,0 (1 + 𝑧)4 + 𝛺𝛬,0 + 𝛺𝑘,0 (1 + 𝑧)2}.
As before a simpler form for the integral is obtained by making the substitution 𝑥 = (1 + 𝑧)-1, which yields
(15.41) 𝜒(𝑧) = 𝑐/𝑅0𝐻0 ∫(1 + 𝑧)-11 𝑑𝑥/√(𝛺𝑚,0𝑥 + 𝛺𝑟,0 + 𝛺𝛬,0𝑥4 + 𝛺𝑘,0𝑥2).
From (14.29) and (14.31), the corresponding luminosity distance 𝑑𝐿(𝑧) and angular diameter distance 𝑑𝐴(𝑧) to the object are given by
𝑑𝐿(𝑧) = 𝑅0(1+ 𝑧)𝑆(𝜒(𝑧)) and 𝑑𝐴(𝑧) = 𝑅(𝑡0)/(1+ 𝑧) 𝑆(𝜒(𝑧)),
where 𝑆(𝜒) is given by (14.12), whereas the proper distance to the object is simply 𝑑(𝑧) = 𝑅0𝑆(𝜒(𝑧)). It is useful to introduce the notation 𝜒(𝑧) = 𝑐𝐸(𝑧)/𝑅0𝐻0, so that 𝐸(𝑧) denotes the integral in (15.41). Using the expression (15.10) to obtain 𝛺𝑘,0, one can then write
𝑅0𝑆(𝜒(𝑧)) = 𝑐/𝐻0 ∣𝛺𝑘,0∣-1𝑆(√∣𝛺𝑘,0∣ 𝐸(𝑧)) for 𝛺𝑘,0 ≠ 0,
𝑅0𝑆(𝜒(𝑧)) = 𝑐/𝐻0 𝐸(𝑧) for 𝛺𝑘,0 = 0,
which allows simple direct evaluation of 𝑑𝐿(𝑧) and 𝑑𝐴(𝑧) in each case.
As was the case in the previous section, for general value of 𝛺𝑚,0, 𝛺𝑟,0 and 𝛺𝛬,0 it is not possible to perform the integral (15.41) analytically an so one has to resort to numerical integration. Figure 15.8 shows plots of dimensionless luminosity distance (𝑐/𝐻0)-1𝑑𝐿(𝑧) (top panel) and dimensionless angular distance (𝑐/𝐻0)-1𝑑𝐴(𝑧) (bottom panel) for various of 𝛺𝑚,0 and 𝛺𝛬,0, assuming that 𝛺𝑟,0 is negligible: the solid, broken and dotted lines corresponds to spatially flat, open and closed models respectively.
The integral (15.41) can be evaluated in some simple cases. As an example, consider Einstein-de-sitter(EdS) model (𝛺𝑚,0 = 1, 𝛺𝑟,0 = 0, 𝛺𝛬,0 = 0). In this case we find
𝜒(𝑧) = 𝑐/𝑅0𝐻0 ∫(1 + 𝑧)-11 𝑑𝑥/√𝑥 = 2𝑐/𝑅0𝐻0 [1- (1 + 𝑧)-1/2].
Thus, the luminosity distance in EdS model is given by
𝑑𝐿(𝑧) = 2𝑐/𝐻0 (1 + 𝑧)[1- (1 + 𝑧)-1/2],
and the angluardiameter distance by
𝑑𝐴(𝑧) = 2𝑐/𝐻0 1/(1 + 𝑧) [1- (1 + 𝑧)-1/2].
We note that 𝑑𝐴(𝑧) has a maximum at redshift 𝑧 = 5/4** and we can find it in Figure 15.8.
What we need to use the above relation are a standard candle and a standard ruler for them to fix the values of 𝛺𝑚,0 and 𝛺𝛬,0. Though they arei very hard to find in the universe, in recent years (of 2005), using distant Type Ia supernovae as standard candles and anisotropies in the cosmic microwave background radiation as a standard ruler. The results of these observation suggest tha we live in a spatially flat universe with 𝛺𝑚,0 ≈ 0.3 and 𝛺𝛬,0 ≈ 0.7.
15.9 The volume-redshift relation .
We found in Section 14.12 that the proper volume in the range 𝜒 → 𝜒 + 𝑑𝜒 and subtending an infinitesimal solid angle 𝑑𝛺 = sin 𝜃 𝑑𝜃 𝑑𝜙 at the observer is
(15.42) 𝑑𝑉0 = 𝑐𝑅02𝑆2(𝜒(𝑧))/𝐻(𝑧) 𝑑𝑧 𝑑𝛺,
where a redshift 𝑧 is given by 𝑑𝑉(𝑧) = 𝑑𝑉0/(1 + 𝑧)3. We may now express 𝑑𝑉0 in terms of 𝐻0, 𝛺𝑚,0, 𝛺𝑟,0 and 𝛺𝛬,0. Using (15.40), (15.38) and (15.10) for 𝜒(𝑧), 𝐻(𝑧) and 𝛺𝑘 respectlvely, we find that
(15.43) 𝑑𝑉0 = (𝑐𝐻0-1)3/𝘩(𝑧) ∣𝛺𝑘,0∣-1𝑆2√ ∣𝛺𝑘,0∣ 𝐸(𝑧) for 𝛺𝑘,0 ≠ 0,
𝑑𝑉0 = (𝑐𝐻0-1)3/𝘩(𝑧) 𝐸2(𝑧) for 𝛺𝑘,0 = 0,
where we define
𝘩(𝑧) ≡ 𝐻(𝑧)/𝐻0 = √{𝛺𝑚,0(1 + 𝑧)3 + 𝛺𝑟,0(1 + 𝑧)4 + 𝛺𝛬,0 + 𝛺𝑘,0(1 + 𝑧)2}, 𝐸(𝑧) ≡ ∫0z 𝑑𝑧/𝘩(𝑧).
One must once again resort to numerical integration to obtain 𝑑𝑉0. In Figure 15.9 we plot the dimensionless differential comoving element (𝑐𝐻0)3𝑑𝑉0/(𝑑𝑧 𝑑𝛺) as a function of redshift, assuming that 𝛺𝑟,0 = 0. In particular, we note that we may explore a large comoving volume in the range 𝑧 = 2-3 for the currently favored case (𝛺𝑚,0, 𝛺𝛬,0) = (0.3, 0.7).
15.10 Evolution of the density parameters .
It is possible to investigate of the evolution of these densities 𝛺𝑚, 𝛺𝑟 and 𝛺𝛬) as the universe expands.
From (15.5) we have the equation of 𝛺𝑖(𝑡) and using Quotient rule we obtain
(15.44) 𝛺𝑖(𝑡) = 8π𝐺/3𝐻2(𝑡) 𝜌𝑖(𝑡) ⇒ 𝑑𝛺𝑖/𝑑𝑡 = 8π𝐺/3𝐻2[ῤ𝑖 - (2Ḣ/𝐻)𝜌𝑖],
where the label 𝑖 denotes '𝑚', '𝑟' or '𝛬' and dots denotes differentiation with respect to cosmic time 𝑡 as usual. From the equation of motion for the cosmological fluid (14.39) we have
ῤ𝑖 = -3(1 + 𝑤𝑖)𝐻𝜌𝑖,
where 𝐻 = Ṙ/𝑅 and the equation-of state parameter 𝑤𝑖 = 𝑝𝑖/(𝜌𝑖𝑐2). Thus {15.44) becomes
(15.44) 𝑑𝛺𝑖/𝑑𝑡 = -𝛺𝑖𝐻[3(1 + 𝑤𝑖) + 2Ḣ/𝐻2].
We now find an expression for Ḣ in 𝑅, Ṙ or Ȑ and the deceleration parameter 𝑞
Ḣ = 𝑑/𝑑𝑡 (Ṙ/𝑅) = Ȑ/𝑅 - (Ṙ/𝑅)2 = Ȑ/𝑅 - 𝐻2, Ḣ/𝐻2 = 𝑅Ȑ/Ṙ2 - 1 = -(𝑞 + 1).
Substituting this result into (14.45) and using (15.14), we finally obtain the neat relation
𝑑𝛺𝑖/𝑑𝑡 = 𝛺𝑖𝐻(𝛺𝑚 + 2𝛺𝑟 - 2𝛺𝛬 - 1 - 3𝑤𝑖),
Setting 𝑤𝑖 = 0, 1/3 and -1 respectively for matter(dust), radiation and the vacuum, we thus obtain
(15.46) 𝑑𝛺𝑚/𝑑𝑡 = 𝛺𝑚𝐻[(𝛺𝑚 -1) + 2𝛺𝑟 - 2𝛺𝛬],
𝑑𝛺𝑟/𝑑𝑡 = 𝛺𝑟𝐻[𝛺𝑚 + 2(𝛺𝑟 - 1) - 2𝛺𝛬],
𝑑𝛺𝛬/𝑑𝑡 = 𝛺𝛬𝐻[𝛺𝑚 + 2𝛺𝑟 - 2(𝛺𝛬 -1)].
By dividing these equations by one another, we may remove the dependence on 𝐻 and 𝑡 and hence obtain a set of copled first-order differentiable equations. Therefore, these equations define a unique trajectory that passes through some points. As an illustration, let us consider the case 𝛺𝑟 = 0. Dividing two equations then gives
𝑑𝛺𝛬/𝑑𝛺𝑚 = [𝛺𝛬{𝛺𝑚 - 2(𝛺𝛬 - 1)}]/[𝛺𝑚{(𝛺𝑚 - 1) - 2𝛺𝛬}],
which define a set of trajectories or 'flow line' in the (𝛺𝑚, 𝛺𝛬) -plane. The equation highlights the significance of the points (1, 0) and (0, 1) which act as 'attractors'. This is illustrated in Figure 15.10.
It is worth noting that the profound effect of a non-zero cosmological constant on the evolution of the density parameters. In case of 𝛬 = 0, any slight deviation from 𝛺𝑚 = 1 in the early universe result in a rapid evolution away from the point (1, 0) along the 𝛺𝑚 axis, tending to (0, 0) for an open universe and to (∞, 0) for a closed one. If 𝛬 > 0, however, the trajectory is 'refocussed' and tends to the spatially flat de Sitter case (0, 1). Indded, by the time 𝛺𝑚 ≈ 0.3 the universe is close to spatially flat.
15.11 Evolution of the spatial curvature .
We may investigate directly the behavior of the spatial curvature from (15.10) as follows
(15.47) 𝛺𝑘 = 1 - 𝛺𝑚 - 𝛺𝑟 - 𝛺𝛬 = - -𝑐2𝑘/(𝐻2𝑅2).
Differentiating the right-hand side with respect to 𝑡 and combining the derivatives (15.46), one finds that
(15.48) 𝑑𝛺𝑘/𝑑𝑡 = 2𝛺𝑘𝐻𝑞 = 𝛺𝑘𝐻(𝛺𝑚 + 2𝛺𝑟 - 2𝛺𝛬),
where 𝑞 is the deceleration parameter. If 𝛺𝛬) = 0, then at some early cosmic time 𝑘 rapidly evolves away from the spatially flat case. In the open case of Figure 15.5 𝛺𝑘 → 1 and in the closed case 𝛺𝑘 → -∞. However if 𝛺𝛬) > 0, at some finite cosmic time the 2𝛺𝛬 term in (15.48) will dominate the others, then 𝛺𝑘 is 'refocussed' back to 𝛺𝑘 = 0.
We may obtain an analytical expression for the 𝑘 as a function of redshift 𝑧. Substituting for 𝑐2𝑘 from (15.47) evaluated at 𝑡 = 𝑡0 and noting that 𝑅0/𝑅 = 1 + 𝑧, we obtain the general formula
𝛺𝑘(𝑧) = [𝐻0(1 + 𝑧)/𝐻(𝑧)]2𝛺𝑘,0.
Using (15.38) for 𝐻(𝑧) then gives
𝛺𝑘(𝑧) = 𝛺𝑘,0/{𝛺𝑚,0(1 + 𝑧) + 𝛺𝑟,0(1 + 𝑧)2 + 𝛺𝛬,0(1 + 𝑧)-2 + 𝛺𝑘,0}
From the above expression we find that even if 𝛺𝑘,0 differs greatly from zero, at very high redshift i.e. in the distant past 𝛺𝑘(𝑧) must have been very close to zero. Since today we measure the value 𝛺𝑘,0 in the range -0.5 to 0.5, this means that at very early epochs 𝛺𝑘 must have been very finely tuned to near zero. This tuning of the initial conditions of expansion is called the flatnedd problem and has no solution within standard cosmological models. However, from our above discussion, the presence of a positive 𝛬 explains why the present universe is close to spatially flat.
15.12 The particle horizon, event horizon and Hubble distance .
It is interesting to consider the extent of the region 'accessible' to some comoving observer at a given cosmic time 𝑡.
[Particle horizon]
Let us consider a comoving observer 𝑂 at comoving coordinates 𝜒 and a emitter 𝐸 at 𝜒1 which emits a photon at 𝑡1 that 𝑂 receives by the time 𝑡 in the condition that 𝜒 < 𝜒1.
Since along the photon path 𝑑𝑠 = 𝑑𝜃 = 𝑑𝜙 = 0, from (14.11), the comoving coordinates 𝜒1 of the emitter 𝐸 is determined by
(15.49) 𝜒1 = 𝑐 ∫t1t 𝑑𝑡'/𝑅(𝑡').
If the integral on the right-hand side diverges as 𝑡1 → 0, then 𝜒1 can be made as large as we please by taking 𝑡1 sufficiently small. In this case, it is possible to receive signals emitted at sufficiently early epochs from any comoving particle. But if the integral converges as 𝑡1 → 0, then 𝜒1 can never exceed a certain value for given 𝑡. In this case our vision of the universe is limited by a particle horizon. The 𝜒-coordinate of the particle horizon is given by
(15.50) 𝜒𝑝𝘩(𝑡) = 𝑐 ∫0t 𝑑𝑡'/𝑅(𝑡')
the corresponding proper distance to the particle horizon is 𝑑𝑝 = 𝑅(𝑡)𝜒𝑝𝘩(𝑡).
On differentiating (15.50) with respect to 𝑡, we have 𝑑𝜒𝑝𝘩/𝑑𝑡 = 𝑐/𝑅(𝑡), which is always greater than zero. Thus the particle horizon of a comoving observer grows as 𝑡 increases, and so the parts of the universe that were not in view previously must gradually come into view. Thus if the universe has a big-bang origin then 𝑅(𝑡1) → 0 as 𝑡1 → 0 and so 𝑧 → ∞. Thus the particle horizon at any given cosmic time is the surface of infinite redshift, beyond which we cannot see.***
We can obtain explicit expression for the paricle horizon in some cosmological models. For example, a matter-dominated model at early epoch obeys 𝑅(𝑡)/𝑅0 = (𝑡/𝑡0)2/3 and a radiation-dominated model obeys 𝑅(𝑡)/𝑅0 = (𝑡/𝑡0)1/2. Substituting these into (15.50) gives the proper distance to the particle horizon at 𝑡 as
𝑑𝑝(𝑡) = 3𝑐𝑡 (matter-dominated), 𝑑𝑝(𝑡) = 2𝑐𝑡 (radiation-dominated),
These proper distances are karger than 𝑐𝑡 because the universe has expanded while the photon has been travelling. Alternatively, if one has an analytical expression for 𝜒(𝑧) for some cosmological model, then 𝜒𝑝𝘩 may be obtained simply letting 𝑧 → ∞.
The particle horizon for common cosmological models illustrates the horizon problem, i.e. how do vastly separated regions display the sam physical characteristic (e.g. the nearly uniform temperature of the cosmic microwave background). This problem is a serous challenge to standard cosmology.
[event horizon]
Although our particle horizon grows as the cosmic time increase, in some cosmological models there could be events that we may never see. Similarly to the particle horizon we use (15.49) and have following expression for the event horizon
𝜒𝑒𝘩(𝑡) = 𝑐 ∫t1tmax 𝑑𝑡/𝑅(𝑡),
So 𝜒𝑒𝘩(𝑡0) is the maximum 𝜒-coordinate that can be reached by a light signal sent by us today.
[Hubble distance]
In a similar way to define the Hubble time 𝐻-1(𝑡) one can define the Hubble distance
𝑑𝐻(𝑡) = 𝑐𝐻-1(𝑡),
which provide a characteristic length scale for the universe. We may also define the comoving Hubble distance
(15.51) 𝜒𝐻(𝑡) = 𝑑𝐻(𝑡)/𝑅(𝑡) = 𝑐/{𝐻(𝑡)𝑅(𝑡)} = 𝑐/Ṙ(𝑡).
The Hubble distance is the length scale at which general-relativistic effects become important; indeed, on length scales much less than 𝑑𝐻(𝑡), Newtonian theory is often sufficient to describe the effect of gravitation. We further note that the proper distance to the particle horizon for standard cosmological model is typically
𝑑𝑝(𝑡) ∼ 𝑐𝑡 ∼ 𝑐𝐻-1(𝑡).
Thus, the Hubble distance is of same order as the particle horizon and so is often described simply as the 'horizon'. But in inflationary cosmologies the particle horizon and the Hubble distance may differ by many order of magnitude. In particular, we note that the partle horizon at time 𝑡 depends on the entire expansion history of the universe to that point, whereas the Hubble distance is defined instantaneously at 𝑡. Moreover, once an object lies within an observer's particle horizon it remains so, but an object can lie within an observer's Hubble distance or outside it according to the situation.
* According to this table we should take the value 13.5 Gyr which is very close to the known value 13.8 Gyr (as of 2015).
** We can solve max{1/(1 + 𝑧) [1- (1 + 𝑧)-1/2]} = 4/27 at 𝑧 = 5/4, (e.g. by using WolframAlpha with iPad).
*** In practice, our view of the universe is not by our particle horizon but by the epoch of recombination occured at 𝑧 ≈ 1500.
※ attention: some rigorous derivation might be required
p.s. 중간에 D. Fleisch & J. Kregenow A Student's Guide to the Mathematics of Astronomy (Cambridge University Press 2013)-강추!-의
'spectrum fundamental' Wien's law & Stefan's law를 비롯해, 자상한 해설의 parallax, angular size, angular resolution, luminosity, magnitude와
흥미로운 Herzsprung-Russell diagram 등을 보충 학습하여, textbook 내용 중 모호했던 몇가지를 비로서 이해하게 되었음. |
|
|





































