|
김관석
|
2020-06-07 16:23:00, 조회수 : 586 |
- Download #1 : F16_3_7.jpg (306.4 KB), Download : 1

16.12 Perturbations from inflation* .
The greatest success of inflation theory is to provide a mechanism by which the fluctuations needed to seed the development of structure within the universe can be generated. The topic is the subject of much current research, and we can meet only a limited treatment here. By dealing the simplest case, namely for a spatially flat universe with a simple 'gauge choice' (see below), we may be able to get a flavor of the physics involved.
The current opinion of how structure in the universe originated is that it was via amplification during a period of inflation, of initial quantum irregularities of the scalar field that drive inflation. We can divide the process into two broad categories. First, we need to work out the equation s of motion for spatial perturbations in the scalar field. This can be done classically, i.e. taking the scalar field as a classical source linked self-consistently to the gravitational field via a classical energy-momentum tensor. Second, we need to derive initial conditions for these perturbations, and this demands that we understand the quantum field theory (QFT) of perturbation themselves. This sounds formidable but actually turns out to consider only the quantum physics of a mass on a spring, albeit one in which the mass changes as a function of time. These topics are discussed in detail in the remainder of this chapter.
16.13 Classical evolution of scalar-field perturbations .
We assume that the scalar field ⱷ**, which hitherto has been a function of cosmic time 𝑡 only, now has perturbations that are function of space and time. We can thus write
(16.19) ⱷ(𝑡) → ⱷ0(𝑡) + 𝛿ⱷ(𝑡, 𝑥̄). (𝑥̄; vector 𝑥)
The Einstein field equations then imply that the Einstein tensor is also perturbed away from its background value. In turn, therefore we must have a metric different from the FRW one assumed so far. Now we must choose 'gauge' (i.e. coordinate system) to make that there is no preferred way to define a spacetime slicing of the universe. For example, we can choose, as a new time coordinate, one for which surface of constant time have a constant value of the new of the new perturbed scalar field on them. This is always possible and, in such a gauge, the spatial fluctuations of ⱷ have apparent totally vanished!※
To meet such problems, methods of gauge-invariant quantities have been developed. We will contact with such methods, when we introduce the so-called 'curvature' perturbations. To reach this point, we first work with a specific simple form of gauge known as the longitudinal or Newtonian gauge, a restricted form, where only one extra function is introduced. The justification for using such a restricted form is that it lead to an Einstein tensor with the correct extra degrees of freedom to match the extra terms in the scalar field energy-momentum tensor arising from the field perturbation.
For a spatially flat (𝑘 = 0) background FRW model we adopt Cartesian comoving coordinates and rite the perturbed metric as
(16.20) 𝑑𝑠2 = (1 + 2𝚽) 𝑑𝑡2 - (1 - 2𝚽) 𝑅2(𝑡) (𝑥2 + 𝑦2 + 𝑧2,
where 𝚽 is a general infinitesimal function of all four coordinates. It assumed smallness means that we only need to consider quantities to first order in 𝚽. For the time being, we simply note that 𝚽 represents the Newtonian potential of the perturbations. For instance, for a spherically symmetric perturbation of mass 𝑀 and radius 𝑟, if we put 𝚽 = -𝐺𝑀/𝑟𝑐2 then the first term recovers the 𝑡𝑡-term of the Schwarzschild metric.
The perturbed Einstein field equations
We now need to find both the new energy-momentum tensor of the scalar field ⱷ and the new Einstein tensor corresponding to our perturbed metric. The first step is to calculate the connection coefficients to corresponding to the perturbed metric (16.20) to first order in 𝚽. Taking the form 𝛤𝜎𝜇𝜈 = (𝛤0)𝜎𝜇𝜈 + 𝛿𝛤𝜎𝜇𝜈 where 𝛤0 is when 𝚽 = 0, the perturbation terms are given by, (omitting the derivation※)
𝛿𝛤00𝜇 = ∂𝜇𝚽, 𝛿𝛤0𝑖𝑖 = -𝑅2(𝑑𝚽/𝑑𝑡 + 4𝛨𝛷), 𝛿𝛤𝑖𝑖𝜇 = -∂𝜇𝚽,
𝛿𝛤𝑗𝑖𝑖 = 𝛿𝑗𝑘∂𝑘𝚽 (for 𝑖 ≠ 𝑗), 𝛿𝛤𝑖00 = 1/𝑅2 𝛿𝑗𝑘∂𝑘𝚽,
where 𝛨 = Ṙ/𝑅 is the Hubble parameter of the unperturbed background, and no sum over repeated 𝑖𝑖. The remaining connection coefficients either follow from symmetry or are zero.
Again the perturbed part of Einstein tensor is given by (omitting the derivation※)
(16.21) 𝛿𝐺0𝑖 = -2∂𝑖(𝑑𝚽/𝑑𝑡 + 𝛨𝚽), 𝛿𝐺00 = -2(𝛻̄2𝚽 - 3𝛨𝑑𝚽/𝑑𝑡 - 3𝛨2𝚽, 𝛿𝐺𝑖𝑖 = -2[𝑑2𝚽/𝑑𝑡2 + 4𝑑𝚽/𝑑𝑡 𝛨 + (2Ḣ + 3𝛨2)𝚽],
where again the remaining connection coefficients either follow from symmetry or are zero. The symbol 𝛻̄̄ denotes the spatial Laplacian, which in this simple flat case is given by
(16.22) 𝛻̄2 = 1/𝑅2 (∂2/∂𝑥2 + ∂2/∂𝑦2 + ∂2/∂𝑧2).
It is worth noting that the time derivative of the Hubble parameter, from (16.21) can be rewritten as
(16.23) Ḣ = -1/2 ᾠ02.
We also need to evaluate the perturbed part of the scalar-field energy-momentum tensor. Substituting (16.0) into (16.7) and working to first order in 𝜀, one finds that
(16.24) 𝛿𝑇0𝑖 = ᾠ0∂𝑖(𝛿𝜔), 𝛿𝑇00 = -ᾠ02𝚽 + ᾠ0𝛿ᾠ + 𝑉'𝛿𝜔, 𝛿𝑇𝑖𝑖 = ᾠ02𝚽 + ᾠ0𝛿ᾠ + 𝑉'𝛿ⱷ,
where 𝑉' = 𝑑𝑉/𝑑ⱷ0 and the remaining connection coefficients either follow from symmetry or are zero.
We may now use the Einstein field equations to relate the Einstein tensor and the scalar -field energy-momentum tensor. Since 𝜅 = 8π𝐺/𝑐4 equals unity in our system, one simply requires that 𝛿𝐺𝜈𝜇 = -𝑇𝜈𝜇. Let us start with the (0𝑖)-components, for which we have the equation and using (16.23) we obtain
(16.25) 2∂𝑖(𝑑𝚽/𝑑𝑡 + 𝛨𝚽) = ᾠ0∂𝑖(𝛿ⱷ)
(16.26) 𝑑𝚽/𝑑𝑡 + 𝛨𝚽 = 1/2 ᾠ0𝛿ⱷ.
For (𝑖𝑖)-components we have the same information, (so omitting (16.27) and (16.28)), but for (00)-components using (16.26) and eliminating 𝑉' then we obtain
(16.29) (ᾠ02 + 2𝛻̄̄2)𝚽 = ᾠ02 𝑑/𝑑𝑡 (𝛿ⱷ/ᾠ0).
Perturbation equations in Fourier space
The result (16.26) and (16.29) are the basic equations relating 𝚽 and 𝛿𝜀. It is convenient to work in terms of the Fourier decomposition of these quantities and analyze what happens to a perturbation corresponding to a given comoving spatial scale. Thus we assume that 𝚽 and 𝛿ⱷ are decomposed into a superposition of plane wave states with comoving wav9evector 𝑘̄, so that, omitting the derivation※,
𝚽(𝑥̄) = 1/(2π)3/2 ∫ 𝚽𝑘̄ exp(𝑖𝑘̄ ⋅ 𝑥̄) 𝑑3𝑘̄,
where 𝑥̄ = (𝑥, 𝑦, 𝑧) and a similar expression hold for 𝛿𝜔. the evolution of a mode amplitude 𝚽𝑘̄ depends only on the comoving wavenumber 𝑘 = ∣𝑘̄∣; the corresponding actual physical wavenumber is 𝑘/𝑅(𝑡). We thus work in terms of 𝚽𝑘 and 𝛿𝜔𝑘. In terms of these variables the action of 𝛻̄̄2 will be just multiply 𝚽𝑘 by -𝑘2/𝑅2(𝑡), whereas the time derivatives remain unchanged. Equations (16.26) and (16.29) therefore become
(16.30) 𝑑𝚽𝑘/𝑑𝑡 + 𝛨𝚽𝑘 = 1/2 ᾠ0𝛿𝜔𝑘, {1 - 2𝑘2/(𝑅2ᾠ02}𝚽𝑘 = 𝑑/𝑑𝑡 (𝛿ⱷ𝑘/ᾠ0).
What we could do next is to obtain a single second-order equation in terms of just one of them. In fact, this leads to rather messy equations and, moreover the results are not gauge invariant, since 𝚽𝑘 or 𝛿ⱷ𝑘 is not gauge invariant on its own.
16.14 Gauge invariance and curvature perturbations .
Gauge invariance is related to how we define spatial ;slices' of the perturbed spacetime. By transforming to a new time coordinate, one can handle perturbations in scalar field at will. there are two ways to achieve it. First, one can choose invariables in such change and definitely describe something physical. These are called gauge-invariant variables. Second, one can use variables which would change if one altered the slicing but which is defined relative to a particular slicing that can itself be defined physically, Then these are also physical variables and are sometimes called gauge invariant a bit confusingly. Note that we concentrate just on change in time coordinate, though changing spatial coordinates is possible.
We start in the first way describing the perturbation in terms of truely gauge-invariant quantities. For any scalar function 𝑓 in spacetime, consider the effects on it of the change in time coordinates 𝑡 → 𝑡' + 𝛥𝑡. We may define a new, perturbed function by follows and to first order in 𝛥𝑡 we may write, without full derivation※
(16.31) 𝑓'(𝑡') = 𝑓(𝑡).
(16.32) 𝑓'(𝑡) = 𝑓'(𝑡' - 𝛥𝑡) ≈ 𝑓(𝑡) - ḟ 𝛥𝑡,
where ḟ can be whether 𝑓 or 𝑓' is being differentiated respect to 𝑡 or 𝑡', since these would be second-order difference. Hence the perturbation in the scalar function due to 'gauge transformation' 𝑡 → 𝑡 + 𝛥𝑡 is given by
(16.33) 𝛥𝑓 = -ḟ 𝛥𝑡.
In order to evaluate the change one must distinguish between the two occurrences of the 𝚽-variable in (16.20). For an arbitrary scalar perturbation, the general form of the metric in fact takes the form
(16.34) 𝑑𝑠2 = (1 + 2𝚿) 𝑑𝑡2 - (1 - 2𝚽) 𝑅2(𝑡) (𝑥2 + 𝑦2 + 𝑧2,
where 𝚿 and 𝚽 are different functions, but for matter with no 'anisotropic stress' (so all the off-diagonal components of the stress-energy tensor are zero), the two function may taken as equal. Hence (16.34) leads to (16.20). However, even in this case the two functions behave differently under gauge transformation. So we need consider only the 𝚽 above, which takes the role of a spatial curvature term. Under 𝑡 → 𝑡 + 𝛥𝑡 we find that
(16.35) 𝑅2(1 - 2𝚽) → 𝑅2(1 - 2𝚽) + [2𝑅Ṙ(1 - 2𝚽) - 2𝑅2𝑑𝚽/𝑑𝑡]𝛥𝑡.
Since both 𝚽 and 𝛥𝑡 are infinitesimal, we may employ the same argument that led to (16.33). Then, to first order, we have, (how? ※)
(16.36) 𝛥𝚽 = 𝛨𝛥𝑡,
where, of course, 𝛨 = Ṙ/𝑅. Thus, for any scalar function 𝑓 with perturbations 𝛿𝑓, we see that the combination
(16.37) 𝛇𝑓 = 𝚽 + (𝛨𝛿𝑓)/ḟ
is gauge invariant under the gauge transformation 𝑡 → 𝑡 + 𝛥𝑡 that are considering, since to the first order we have
(16.38) 𝛇𝑓 → 𝛇'𝑓 = 𝚽 + 𝛨𝛥𝑡 + {𝛨(𝛿𝑓 - ḟ 𝛥𝑡)}/ḟ = 𝛇𝑓.
Thus, for the specific example of our scalar-field perturbation 𝛿𝜀, we may identify the corresponding gauge-invariant quantity as
(16.39) 𝛇 = 𝚽 + (𝛨𝛿ⱷ)/ᾠ0.
We will therefore use this variable or its Fourier transform from now on in the later section. This quantity is called the curvature perturbation.
Let us discuss the route for physically meaningful perturbation variable. This route can be illustrated directly with the 𝚽-function, and one begins by defining the quantity
(16.40) 𝓡 ≡ -𝚽∣co,
where the subscript indicates that 𝚽 is to be evaluated on comoving slices. By 'comoving' we mean a time-slicing that is orthogonal to the worldlines of the 'fluid' that makes up the matter. For an ordinary fluid, this would amount to choosing frames in which, at each instant and position, the fluid appears to be at rest. The same applies here and, because the frame involved is physically defined, the variable 𝓡, which measures the spatial curvature in the given frame, is itself physically well defined. Thus the quantity 𝓡 is also called the 'curvature perturbation' in the literature. As we now show, it is in fact equal to minus the variable 𝛇 in (16.39).
For any scalar density perturbation 𝛿𝜌, one can write the spatial curvature in comoving slice as
(16.41) 𝓡 = -𝛇𝜌 + (𝛨𝛿𝜌co)/ῤ.
Let us consider what happen for the particular case of a perturbation in a scalar field. In (16.24) the (0𝑖)-components of the perturbed stress-energy tensor read
(16.42) 𝛿𝑇0𝑖 = ᾠ0∂𝑖(𝛿𝜔).
In the comoving frame, this momentum density must vanish, by definition, and so the scalar-field perturbation cannot depend on the spatial coordinates and thus variables. Hence, for a scalar field, we have
(16.43) 𝓡 ≡ -𝛇.
16.15 Classical evolution of curvature perturbations .
We now consider the evolution of the Fourier transform of the gauge-invariant perturbation (16.39), namely
(16.44) 𝛇𝑘 ≡ 𝚽𝑘 + (𝛨𝛿ⱷ𝑘)/ᾠ0.
Using (16.30), the second-order differential equation satisfied by this quantity is quite simply shown to be, (omitting the derivation※),
(16.45) 𝑑2𝛇𝑘/𝑑𝑡2 + (ᾠ02/𝛨 + 2ᾥ0/ᾠ0 + 3𝛨)𝑑𝛇𝑘/𝑑𝑡 + 𝑘2/𝑅2 𝛇𝑘 = 0.
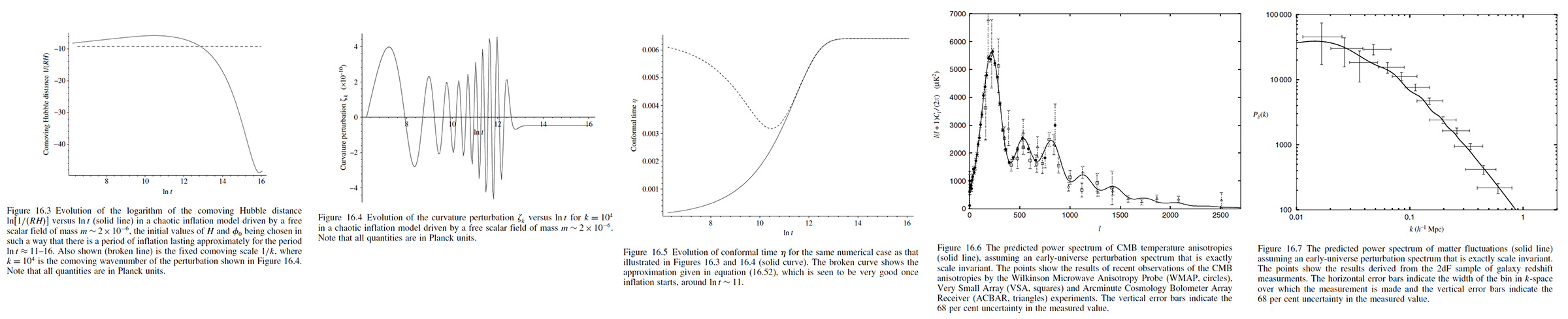
Given a potential 𝑉(ⱷ0) and some initial conditions for 𝛨 and ⱷ0, we can integrate the background evolution equations numerically and obtain 𝛨 and 𝜔0 as functions of cosmic time 𝑡. If we simultaneously integrate 𝛇𝑘 using (16.45), we can thereby trace the evolution of the curvature perturbation over the time period of interest. An example of the results of this procedure is shown in Figure 16.3 and 16.4, for 𝑉(ⱷ0) = 1/2 𝑚2ⱷ02 (chaotic inflation) with 𝑚 ~ 2 ⨯ 10-6 (a typical value in such theories). The period ln 𝑡 ≈ 11-16 for the inflation and the comoving wavenumber of the perturbation was chosen as 𝑘 = 104.
From Figure 16.3, one can see the universe is inflating during that period, since comoving Hubble distance 1/(𝑅𝛨), which is called the 'horizon' in inflationary theory, is decreasing. The broken line in From Figure 16.3 is the natural logarithm of the reciprocal of the comoving wavenumber 𝑘, which is of course constant for a given perturbation.. This reciprocal, 1/𝑘, can be thought of as the comoving wavelength scale of the perturbation itself.
The behavior of the curvature perturbation 𝛇𝑘 is shown in Figure 16.4 for 𝑘 = 104 and can be understood from the behavior of the'horizon' or
the comoving Hubble distance in Figure 16.3. Whilst the perturbation scale 1/𝑘 is less than the horizon radius 1/(𝑅𝛨) the curvature perturbation 𝛇𝑘 just oscillates. Once 1/(𝑅𝛨) has dropped below 1/𝑘, we see that the perturbation suddenly 'freeze' and no longer oscillates. We speak of this moment as the perturbation ;leaving the horizon' and in intuitive terms, we can understand that beyond this point the perturbation is no longer able to feel its own self-gravity, since it is larger than the characteristic scale over which physical process in the universe operate coherently. If much later in history of the universe when the horizon catches up with 1/𝑘 again, the perturbation is said to 're-enter the horizon' and oscillations will begin again. (though it is not expected that there will be the scalar field itself, since it is though to decay into other particles via the process of reheating, shortly after inflation ends.
The key point to note is that, via inflation, one has produced 'super-horizon' scale fluctuation in the early universe. These fluctuations later go on to provide the seeds for galaxy formation and the perturbation in the cosmic background (CMB) radiation that we observe today. By studying the distribution of galaxies and CMB fluctuation as a function of scale, it is possible to obtain an idea of the underlying primordial spectrum of perturbation that produced them. Thus, by predicting this primordial spectrum spectrum, we can perform a test of the whole inflationary picture for the origin of fluctuation. We can give only a simplified treatment , but the basic equations are within our reach, we now discuss.
16.16 Initial conditions and normalization of curvature perturbations .
The key concept is the question: what sets the initial conditions for the perturbation 𝛇𝑘 itself? If we know this for each for each 𝑘, then we could compute a spectrum of curvature perturbation as a functions of 𝑘.
The basic Idea for setting the initial conditions is that they come from quantum-field- theoretic fluctuations in the value of scalar field ⱷ. Thus the 'classical' perturbations discussed above need to be quantized. A rigorous way of quantization has been developed.*** Although the process is complicate , the final result in our case is very simple. To apply the result, we must first make two changes of variables.
• Convert from cosmic time 𝑡 to a new dimensionless time variable 𝜂 known as 'conformal time' and defined 𝑑𝜂/𝑑𝑡 = 𝑐/𝑅.
• Convert from the curvature perturbation 𝛇𝑘 to a new variable 𝛏𝑘 given by 𝛏𝑘 = 𝛼𝛇𝑘, where 𝛼 = 𝑅ᾠ0/𝛨.
The correct quantization may achieved simply by treating 𝛏𝑘 as a free complex scalar field and quantizing it in the standard fashion. The evolution for the quantum perturbations turns out to be identical to the 'classical' equation for 𝛏𝑘. Thus having fixed initial conditions for 𝛏𝑘 quantum mechanically, one may follow the classical evolution.
Making the transformation of variables above, equation (16.45) becomes even simpler. In particular, the variable 𝛼 was chosen in order to remove the first derivative term there, so as to make it more like a simple harmonic oscillator equation. Using a prime to denote a derivative with respect to conformal time, we obtain, omitting the derivation※
(16.46) 𝛏𝑘" + (𝑘2 - 𝛼"/𝛼)𝛏𝑘 = 0.
It is now clear that we are dealing with the equation for 𝑘-th mode of a scalar field with a time-variable mass given by 𝑚𝜉2 = -𝛼"/𝛼. How?※ The explicit expression for this effective mass is given in terms of the background quantities by, omitting the derivation※
(16.47) 𝑚𝜉2 = ⱷ0'2/2 - 2ⱷ0'2ⱷ0"2/𝑅𝛨 - ⱷ0'4/(2𝑅2𝛨2) - ⱷ0'''/ⱷ0',
(16.48) = -2𝑅2𝛨2[1 + ᾠ02/2𝛨2 + ᾠ04/4𝛨4 + ᾠ0ᾥ0/𝛨3 + 3ᾥ0/(2𝛨ᾠ0) + 𝑑3ⱷ/𝑑𝑡3{1/(2𝛨2ᾠ0)}].
In the 'slow-roll' approximation, ᾥ0 and higher derivatives were neglected. Furthermore, we assume that ᾠ0 ≪ 𝛨 during the periods of interest. In this case 𝑚𝜉2 ∼ and -2𝑅2𝛨2 and (16.46) becomes
(16.49) 𝛏𝑘" + (𝑘2 - 2𝑅2𝛨2)𝛏𝑘 = 0.
In this form, we can see the origin of the behavior discussed above in terms of a perturbation 'leaving the horizon'. When 𝑘 ≫ 𝑅𝛨, since 1/𝑘 ≫ 1/(𝑅𝛨), the perturbation length scale is within the horizon and we have oscillatory behavior. When 𝑘 ≪ 𝑅𝛨, the perturbation length scale exceeds the horizon and we have exponential growth in 𝛏𝑘. Moreover, we see that if 𝑘 can be neglected, we may deduce the solution 𝛏𝑘 ∝ 𝛼. Since 𝛏𝑘 = 𝛼𝛇𝑘, this means that the curvature perturbation 𝛇𝑘 is constant, which is exactly the behavior seen in Figure 16.4.
In the regime 𝑘 ≫ 𝑅𝛨, (16.49) becomes simply the harmonic oscillator equation 𝛏𝑘" + 𝑘2𝛏𝑘 = 0, the quantization of which is well understood. This quantization demands that the norm of any state evaluates to unity in Plank units, or equivalently that the conserved current of the field 𝜒 is unity, so that, (though we need some more explanations※)
(16.50) -𝑖(𝜒𝜒'* - 𝜒𝜒*) = 1,
where 𝜒* or 𝜒'* is the complex conjugate of 𝜒 or 𝜒' respectively. It is this condition that sets the absolute scale of the perturbations. Hence, the properly normalized positive-energy solution in the regime 𝑘 ≫ 𝑅𝛨 is given (up to a constant phase factor) by, (similar to wavefunction of Schrodinger equations※)
(16.51) 𝛏𝑘 = 1/√(2𝑘) exp(-𝑖𝑘𝜂),
which is therefore the form to which any solution of (16.49) must tend well within the horizon.※
In order to obtain a full solution to (16.49), consider to manipulating the conformal time 𝜂 carrying out an integration by parts:
𝜂 = ∫ 𝑑𝑡/𝑅 = ∫ 𝑑𝑅/𝑅2𝛨 = [- 1/𝑅𝛨] - ∫ 𝑑𝛨/𝑅𝛨2
= [- 1/𝑅𝛨] - ∫ Ḣ/𝛨2 𝑑𝑅/𝑅2𝛨2
= [- 1/𝑅𝛨] + ∫ ᾠ02/2𝛨2 𝑑𝑡/𝑅.
Again ignoring a term in ᾠ02/2𝛨2, we can thus write
(16.52) 𝜂 = 𝜂end - 1/𝑅𝛨,
where 𝜂end is the value at which the conformal time saturates at the end of inflation (that it does indeed saturate is obvious from the facts that 𝑑𝜂/𝑑𝑡 = 1/𝑅 and that 𝑅 is increasing exponentially during inflation). Figure 16.5 shoes that (16.52) is indeed a good approximation during inflation in our current numerical example. Equation (16.49) now becomes
(16.53) 𝛏𝑘" + [𝑘2 - 2/(𝜂end - 𝜂)2]𝛏𝑘 = 0,
which finally is exactly soluble. There is a unique solution (up to a constant phase factor) that tends to (16.51) for small 𝜂; it is given by
(16.54) 𝛏𝑘 = 1/√(2𝑘3) [{𝑖 + 𝑘(𝜂end - 𝜂)}/(𝜂end - 𝜂)] 𝑒-𝑖𝑘𝜂.
By inspection this has the correct property for 𝜂 ≪ 𝜂end provided that 𝑘𝜂end ≫ 1. Comparison with Figure 16.5 shows that this is indeed the case for 𝑘-values of interest (for the figure 𝑘 = 104 and 𝜂end ≈ 0.64).
Now that we have a correctly normalized general solution for 𝛏𝑘, let us the regime 𝑘 ≪ 𝑅𝛨 at which the perturbation length scale exceeds the horizon. We use (16.52) to rewrite the solution just found as
(16.55) 𝛏𝑘 = 1/√(2𝑘3) (𝑘 + 𝑖𝑅𝛨)𝑒𝑖𝑘/𝑅𝛨 ≈ 𝑖𝑅𝛨/√(2𝑘3).
Thus, for such modes,
(16.56) 𝛇𝑘 = 𝛏𝑘/𝛼 ≈ 𝑖/√(2𝑘3) 𝛨2/ᾠ0.
Since we know that 𝛇𝑘 is constant after the mode has left the horizon, this means we are free to evaluate the right-hand side at the horizon exit itself. We therefore write schematically
(16.57) 𝛇𝑘 ≈ 𝑖/√(2𝑘3) (𝛨2/ᾠ0)∣𝑘=𝑅𝛨
This is a famous and important result in inflationary theory; it gives the (constant) value of the amplitude of the plane-wave curvature perturbation having comoving wavenumber 𝑘 for modes whose length scale exceeds the horizon.
16.17 Power spectrum of curvature perturbations .
From (16.57) we can deduce an expression for the power spectrum 𝓟𝛇(𝑘) of the primordial curvature perturbation, In the most commonly used definition the power spectrum of a spatially varying field is defined as the contribution to the total variance of the field per unit logarithmic interval in 𝑘. Thus we define 𝓟𝛇(𝑘) such that
(16.58) <𝛇(𝑥̄)𝛇*(𝑥̄)> = ∫0∞ 𝓟𝛇(𝑘) 𝑑(ln 𝑘), <𝛇𝑘𝛇𝑘*> = <∣𝛇𝑘∣2>,
where <∙ ∙ ∙> denotes an expectation value and the total spatial variation of the curvature perturbations is given, (though we need some more explanations※)
(16.59) 𝛇(𝑥̄) = 1/(2π)3/2 ∫ 𝛇𝑘̄ exp(𝑖𝑘̄ ∙ 𝑥̄) 𝑑3𝑘̄.
In these expressions, 𝑥̄ refers to comoving coordinates and 𝑘 = ∣𝑘̄∣. Evaluating <𝛇(𝑥̄)𝛇*(𝑥̄)>, and remembering that 𝑑3𝑘̄ = 4π𝑘2 𝑑𝑘, on finds that (16.58) is satisfied providing that
<𝛇(𝑥̄)𝛇*(𝑥̄)> = 2π2/𝑘3 𝓟𝛇(𝑘) 𝛿(3)(𝑘̄ - 𝑘̄'),
where 𝛿(3)(𝑘̄ - 𝑘̄') is the 3-dimensional delta function※. We may therefore write 𝓟𝛇(𝑘) = 𝑘3<∣𝛇𝑘∣2>/(2π2) and, using (16.57), we finally obtain
(16.60) 𝓟𝛇(𝑘) = [𝐻2/(2πᾠ0)]2𝑘=𝑅𝐻
In the slow-roll approximation, 𝐻 is only slowly decreasing whilst ᾠ0 is approximately constant. To a first approximation the power spectrum is constant. Such a spectrum is called scale invariant and was proposed in the late 1960s as being the most likely to lead to structure appropriately distributed over the scales we see today. It is known as a Harrison-Zel'dovich spectrum. Here we can see it emerging as a prediction of inflation. However, during inflation, 𝐻 is slowly declining, ᾠ0 is approximately constant and 𝑅 is increasing exponentially. Thus modes with higher 𝑘, which leave the horizon later in time, have a slightly lower value of 𝓟𝛇(𝑘) since 𝐻 is lower there. As a result, the spectrum is predicted to be slightly declining as a function of 𝑘. This is a generic prediction of inflation (assuming that the slow-roll is an accurate model).
We are going to re-derive this result in a enlightening manner. For a scalar field in Minkowski spacetime, the zero-point uncertainty fluctuation is given by,※
(16.61) 𝛿ⱷ𝑘p ≈ 1/𝑉1/2 𝑒-𝑖𝑘p𝑡/√(2𝑘p)
for a mode with wavenumber 𝑘p, where 𝑉 is a normalizing volume. Because in our expanding FRW spacetime 𝑘 = 𝑅𝑘p and an obvious length scale for the normalizing volume is the scale factor 𝑅, we assume that
(16.62) 𝛿ⱷ𝑘 ≈ 𝑒-𝑖𝑘𝑡/𝑅/{𝑅√(2𝑘)}.
As explained above 𝓟𝛇(𝑘) = 𝑘3<∣𝛇𝑘∣2>/(2π2), the corresponding power spectrum of the fluctuations 𝛿ⱷ𝑘 is obtained by multiplying its squared norm by 4π𝑘3/(2π)3 which gives※
(16.63) 𝓟ⱷ(𝑘) = (𝑘/2π𝑅)2𝑘=𝑅𝐻 = (𝐻/2π)2.
We have evaluated the second expression at the 'horizon crossing' value of 𝑘, 𝑅𝐻, since fluctuations on larger length scales are 'frozen in' at the value they reached at this point. To translate this result into the power spectrum of curvature perturbation 𝓡, we need to link 𝓡 and 𝛿ⱷ. Consider 𝛥𝑡 would be needed to move from the 'comoving slicing', in which 𝛿ⱷ vanishes, to a 'flat slicing', in which 𝚽 vanishes. Since 𝛇, as defined in (16.39), remain constant in this process, we see that, in this case,
(16.64) 𝛥𝚽 = 𝚽 = -𝓡 = 𝐻𝛥𝑡 and 𝛥ⱷ = 𝛿ⱷ = -ᾠ0𝛥𝑡,
Eliminating 𝛥𝑡 we find that 𝓡 = 𝐻𝛿ⱷ/ᾠ0 and hence we recover the result, (omitting the detailed process※)
(16.60) 𝓟𝓡(𝑘) = 𝓟𝛇(𝑘) = [𝐻2/(2πᾠ0)]2𝑘=𝑅𝐻
16.18 Power spectrum of matter-density perturbations .
From (16.40) one finds a spectrum of curvature perturbation is the equivalent to the spectrum of fluctuations in the gravitational potential 𝚽 in a comoving slicing. These in turn may be related to the corresponding fluctuations 𝛿𝜌 in the matter density. The full general-relativistic equations describing the evolution under gravity of these density fluctuations may be obtained by repeating all the above discussion for a perfect fluid rather than a scalar field. We merely note the resulting equations, without calculation here※. Except the case on super-horizon scale, on sub-horizon scale, to a good approximation we may take these potential fluctuations as obeying the perturbed Poisson's equation in Newtonian gravity,
𝛻̄2(𝚽) = 4π𝐺(𝛿𝜌).
Since the gravitational field associated with the perturbation is weak, we can expect the Newtonian theory to be a good approximation on sub-horizon scales.
It is more common to work in terms of the fractional-density fluctuation 𝛿 ≡ 𝛿𝜌/𝜌0, where 𝜌0 is the background matter density. Thus, working in Fourier space, we have
𝚽𝑘 = 4π𝐺𝜌0𝑅2/𝑘2 𝛿𝑘,
Because we are considering the simple spatially flat case, using (15.12a) 𝜌0 = 3𝐻2/(8π𝐺), we see that
(16.66) 𝛿𝑘 = -2/3 (𝑘/𝑅𝐻)2𝚽𝑘,
from which we deduce that <∣𝛿𝑘∣2> ∝ 𝑘4<∣𝚽𝑘∣2>. Therefore, defining the matter power spectrum by 𝑃𝛿(𝑘) ≡ <∣𝛿𝑘∣2>, we find 𝑃𝛿(𝑘) ∝ 𝑘𝓟𝓡(𝑘). Since 𝓟𝓡(𝑘) is roughly constant for slow-roll inflation, we thus obtain
(16.67) 𝑃𝛿(𝑘) ∝ 𝑘.
In general, the matter power spectrum is parameterized as 𝑃𝛿(𝑘) ∝ 𝑘𝑛, where 𝑛 is known as the primordial spectral index. We therefore see that inflation naturally predicts 𝑛 = 1, which is also known as the Harrison-Zel'dovich spectrum.
An alternarive way of characterizing this spectrum is from (16.66), if we evaluates the perturbation spectrum when a giben scale re-enters the horizon (𝑘 = 𝑅𝐻) then
𝛿𝑘 ∝ 𝚽𝑘.
Since the spectrum 𝓟ⱷ(𝑘) in (16.63), which is an another matter power spectrum evaluated differently at horizontal entry, is roughly constant, Harrison-Zel'dovich spectrum is also known scale-invariant spectrum. The fractional-density perturbations, as they enter the horizon, make a constant contribution to the total variance per unit logarithmic interval of 𝑘.
Finally, we note form (16.66) that, at a given 𝑘, the time evolution of the fractional-density perturbation 𝛿𝑘 is given by
𝛿𝑘 ∝ 1/(𝑅𝐻)2.
Since for a radiation-dominated model we have 𝑅 ∝ 𝑡1/2 and 𝐻 = 1/(2𝑡), whereas for a matter-dominated model 𝑅 ∝ 𝑡2/3 and 𝐻 = 2/(3𝑡), we find
𝛿𝑘(𝑡) ∝ 𝑡 (radiation-dominated),
𝛿𝑘(𝑡) ∝ 𝑡2/3 (matter-dominated),
which provides a quick derivation of the time dependence of what is known as the growing mode of the matter-density perturbations.
16.19 Comparison of theory and observation .
Here we are going to see two brief illustrations. Figure 16.6 shows the predition for the power spectrum of anisotropies in the cosmic microwave backgroubd (CMB) radiation, assuming That the early-universe perturbation spectrum is scale invariant.The anisotropies in the temperature of the CMB radiation provide a 'snapshot' of the (projected) density perturbations at epoch of recombination (𝑧rec ≈ 1500). The CMB anisotropies over the sky are usually decomposed of spherical harmonics as
𝛥𝑇(𝜃, 𝜙) = ∑∞𝑙=2 ∑𝑙𝑚=-𝑙 𝑎𝑙𝑚𝑌𝑙𝑚(𝜃, 𝜙),
where the 𝑙 = 0 (constant) and 𝑙 = 1 (dipole) terms are usually ignored, since the former is unrelated to the anisotropies and the latter is due to the pecular velosity of the Earth with respect to the comoving frame of the CMB.The power in the fluctuations as a function of angular scale is therefore characterised by the spectrum
𝐶𝑙 = 1/(2𝑙 + 1) ∑𝑙𝑚=-𝑙 ∣𝑎𝑙𝑚∣2.
The characteristic peaks in the predicted CMB power spectrum (solid line) are a consequence of another feature of inflation that all modes outside the horizon are frozen and can only start to oscillate once they re-enter the horizon later in the universe's evolution. This means that a 'phasing up' is able to occure, in which all modes of interest start from effectively a 'zero velocity' state they begin the oscillations during the epoch of recommbination, that lead to the CMB imprints.This is what enables peak to be visible in the power spectrum, with modes on different scales able to complete a different number of oscillations before the end of recommbination. Coherence, leading to peaks, is maintained since each mode has the same starting conditions.This is only possible if the modes of interest are indeed on super-horizon scales prior to recombination, and the only known way of achieving this is via inflation. Thus the peaks visible in Figure 16.6 are a powerful means of testing for inflation. The points shown in the figure are the results of recent observations by the WMAP (circle), VSA (square) and ACBAR (triangles) experiments, which yields a very impressive confirmation of the peak structure and thereby a direct confirmation that inflation occurred.
The primordial matter power spectrum 𝑃𝛿(𝑘) in (16.67) is modified by the evolution under gravity of the perturbations once they re-enter the horizon. This effect may be calculated and the predicted matter power spectrum is shown as the solid line in Figure 16.7. Once again we see that the predicted spectrum has oscillations resulting from a mechanism analogous to that of the CMB discussed above. The points in the figure show the measurements derived from the 2dF (2 degree field) sample of galaxy redshift measurements. Again, a good fit to the data is visible, and time will tell whether the detailed dynamics of inflation, which can be measured by the departures from scale invariance, will become accessible from the combination of data of this type and future CMB experiments.
* Textbook: M.P. Hobson, G. Efstathiou and A.N. Lasenby General Relativity An Introduction for Physicists (Cambridge University Press 2006)
** The 𝜙 in the textbook is replaced by ⱷ for using ᾠ or ᾥ which denotes the first or second time derivative.
*** V.F. Mukhanov, H.A. Feldman & R.H. Brandenberger Theory of cosmological perturbations (Physics Reports 215, 203-333, 1992)
※ attention: some rigorous derivation might be required
p.s. 추후에 Fourier decomposition/wave equation을 별도로, gauge 관련은 Chapter 17를 읽어야 잘 이해될 듯 ...
또한 expectation value, 3-dimensional delta function 등을 학습하려면 너무 오래 걸릴 것이라서 개념적 파악으로만 마쳤음.
상위 inflation and primordial perturbations 이론은 V. Mukhanov Physical Foundation of Cosmology (2005) 참조
범위가 일부 quantum mechanics와 quantum field theory까지 확장됨! 앞으로 기초라도 학습해야..ㅎ |
|
|





































