|
김관석
|
2018-06-22 00:35:54, 조회수 : 4,563 |
- Download #1 : maxwell_eq_s.jpg (92.2 KB), Download : 2
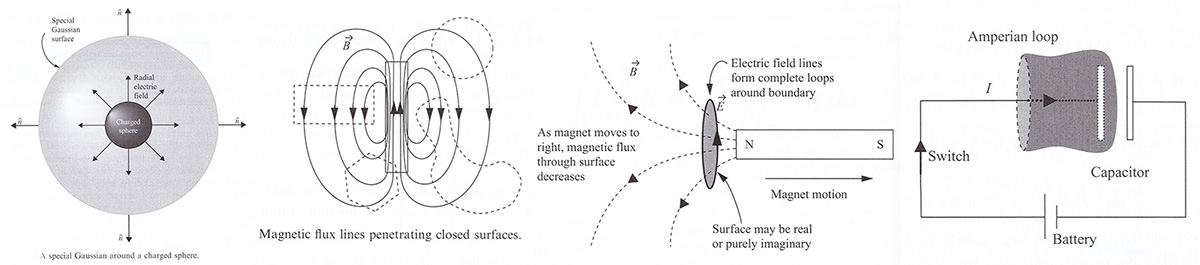

1862년 Foucault는 광속을 측정하였고, 1865년 Maxwelldm 전자기파의 속도가 광속과 같음을 발견했습니다.
전자기파-광속을 수리물리학적으로 이해하는 것이 상대성이론 이해의 바탕이 되므로 그 과정을 간결하게 여기에 정리해 놓습니다
Einstein의 중력장 이론은 Maxwell의 전자기장 이론에서 출발하였으므로 학습할 때 아래 설명이 도움이 될 수 있습니다.
이를 위해서는 벡터 Dot product(내적), Cross product(외적), Del(𝛁), Gradient(기울기), Divergence(발산), Curl(회전)등의 개념이 필요합니다.
다음으로 물리학에서 Maxwell의 방정식을 각각 integral form(적분형)과 differential form(미분형)으로 모두 이해하여야 합니다.
빛의 파동방정식에 대해서 풀면 전자기파의의 속도가 산출되는데 그 결과가 광속 2.9979 *108 m/s입니다!
[기본 수학적 정의/정리]
Dot product: 𝐚 ∙ 𝐛 = |𝐚||𝐛|cos𝜃 <- ∙ (dot), 대수적 정의(a1b1+ a2b2+...+anbn)의 결과
Cross product: 𝐚 × 𝐛 = |𝐚||𝐛|sin𝜃 <- × (cross)
Del: 𝛁 ≡ 𝐢 ∂/∂x + 𝐣 ∂/∂y + 𝐤 ∂/∂z <- 𝛁 (Nabla) [del]
Gradient: 𝛁 Ψ ≡ 𝐢 ∂Ψ/∂x + 𝐣 ∂Ψ/∂y + 𝐤 ∂Ψ/∂z <- Ψ (psi)
* The gradient indicates the rate of spacial change of the field at a point and the direction of steepest increase from that point.[vector result]
Divergence: 𝛁 ∙ 𝐀 ≡ ∂𝐀x /∂x + ∂𝐀y /∂y + ∂𝐀z /∂z
* The divergence indicates the tendency of the field to flow away from a point. [scalar result]
Curl: 𝛁 × 𝐀 ≡ (∂𝐀z /∂y - ∂𝐀y /∂z) 𝐢 + (∂𝐀x /∂z - ∂𝐀z /∂x) 𝐣 + (∂𝐀y /∂x - ∂𝐀x /∂y) 𝐤
* The curl indicates the tendency of the field to circulate around a point and the direction of axis of greatest circulation.[vector result]
[관련 수학적 정리]
Curl of Gradient: 𝛁 × 𝛁 Ψ = 0
Laplacian = Divergence of Gradient: 𝛁 ∙ 𝛁 Ψ = 𝛁² Ψ = ∂²Ψ/∂x² + ∂²Ψ/∂y² + ∂²Ψ/∂z²
Curl of the curl: 𝛁 × (𝛁 × 𝐀) = 𝛁 (𝛁 ∙ 𝐀) - 𝛁² 𝐀
The Divergence theorem ∲s 𝐀 ∙ ň da = ∫v (𝛁 ∙ 𝐀) dV
* The flux of a vector field through a closed surface S is equal to the integral of the divergence of that field over a volume V for which S is a boundary.
Stokes' theorem ∲c 𝐀 ∙ d𝒍 = ∫s (𝛁 × 𝐀) ∙ ň da
* The circulation of a vector field over a closed path C is equal to the integral of the normal component of the curl of that field over surface S for which C is boundary.
[Maxwell의 방정식(Maxwell's Equation)]
1) Gauss's law for electrical fields: ∮s 𝑬 ∙ ň da = q /𝜖₀ [ň: unit normal vector, 𝑬: electric field in volts V/m, q: charge, 𝜖₀: permittivity of free space(진공 유전율)]
* Electric charge produces an electric field, and the flux of that field passing through any closed surface is proportional to the total charge contained within that surface.
applying the divergence theorem -> 𝛁 ∙ 𝑬 = 𝜌/𝜖₀ [𝜌: charge density(전하 밀도) coulombs C/m³]
* The electric field produced by electric charge diverges from positive charge and converges upon negative charge.
2) Gauss's law for magnetic fields: ∮s 𝑩 ∙ ň da = 0 [𝑩: magnetic field in tesla T]
* The total magnetic flux passing through any closed surface is zero.
applying the divergence theorem -> 𝛁 ∙ 𝑩 = 0
* The divergence of the magnetic field at any point is zero.
3) Faraday's law: ∮c 𝑬 ∙ d𝒍 = - d/dt (∫s 𝑩 ∙ ň da) = - ∫s (∂𝑩/∂t) ∙ ň da <- emf: electromotive force(유도기전력)
* Changing magnetic flux through a surface induces an emf in any boundary path of that surface, and a changing magnetic field induces a circulating electric field.
applying Stoke's theorem -> 𝛁 × 𝑬 = - ∂𝑩/∂t
* A circulating electric field is produced by a magnetic field that changes with time.
4) Ampere-Maxwell law: ∮c 𝑩 ∙ d𝒍 = 𝜇₀ [𝑱 + 𝜖₀ d/dt (∫s 𝑬 ∙ ň da)] [𝜇₀: magnetic permittivity of free space(진공 투자율), 𝑱: electric current in amperes A] <- μ(mu)
* An electric current or a changing electric flux through a surface produce a circulating magnetic field around any path that bounds that surface.
applying Stokes' theorem -> 𝛁 × 𝑩 = 𝜇₀ (𝑱 + 𝜖₀ ∂𝑬/∂t) [𝑱: current density(전류 밀도) A/m²]
* A circulating magnetic field is produced by an electric current and by an electric field that changes with time.
[파동방정식(The Wave Equation)과 전자기파 속도]
𝛁²𝑨 = (1/𝑣²) ∂²𝑨/∂t² <- 파동방정식(the wave equation), 𝑣: velocity of wave
𝛁 × (𝛁 × 𝑬) = 𝛁 × (- ∂𝑩/∂t) = - ∂(𝛁 × 𝑩)/∂t <- 3) Faraday's law 양변에 '𝛁 ×' 적용
𝛁 × (𝛁 × 𝑨) = 𝛁 (𝛁 ∙ 𝑬) - 𝛁²𝑨 <- applying curl of the curl
𝛁 ∙ 𝑬 = 𝜌/𝜖₀; 𝛁 × 𝑩 = 𝜇₀ (𝑱 + 𝜖₀ ∂𝑬/∂t) <- Maxwell's equation 1) 4) 에서
𝜌 = 0, 𝑱 = 0 <- free region 속이므로
𝛁²𝑬 = 𝜇₀ 𝜖₀ ∂²𝑬/∂t²; 𝛁²𝑩 = 𝜇₀ 𝜖₀ ∂²𝑩/∂t²
∴ [𝑬/𝑩] 1/𝑣² = 𝜇₀ 𝜖₀, 𝑣 = √ (1/𝜇₀ 𝜖₀) = √ 1/[(4π *10-7 m kg/C²)(8.8541878 *10-12 C² s²/kg m³)] = 2.9979 *108 m/s !
이는 Newton의 물리학 법칙으로는 설명되지 않았으므로 현대과학 발전에 막대한 영향력을 가져온 사건이라 하겠습니다.
그것이 알려진 광속과 일치했으므로 빛도 전자기파임을 알게 되었으며, Einstein이 특수상대성 이론을 도출하는 계기가 되었습니다.
국제단위계(SI)에서는 1983년 1미터를 빛(전자기파)이 진공에서 1/299,792,458초간 진행한 경로의 길이로 정하였습니다.
* 참고문헌: Daniel A. Fleisch A Student's Guide to Maxwell's Equation (Cambridge University Press 2008) |
|
|





































