|
김관석
|
2018-07-05 06:34:14, 조회수 : 22,822 |
- Download #1 : SR3.jpg (59.2 KB), Download : 1

Special Relativistic Mechanics(특수상대성 역학)
* 앞으로는 상대성이론에서 일반화 된 시간 대신 광속 c (299 792 458 m/s) = 1 단위 거리(units length)로 환산하는 질량-길이 시스템 ML(mass-length) system을 주로 사용합니다.*
5.1 4벡터(Four-Vectors)
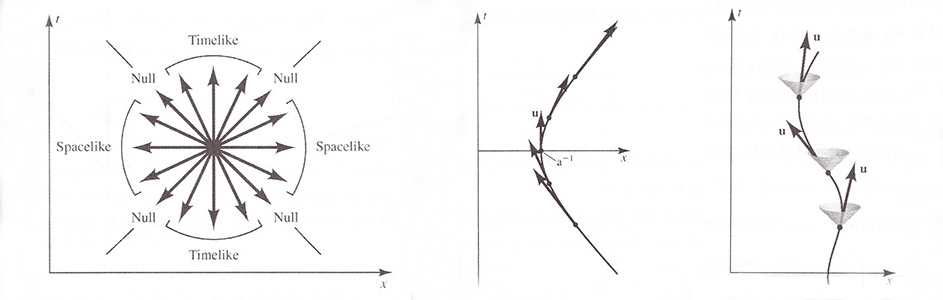
4-벡터(four-vectors)란 4차원 시공간 벡터이며 그림처럼 시간꼴(timelike), 공간꼴(spacelike), 널(null) 4-벡터가 있으며, 널 4-벡터는 비유클리드 기하에서 길이가 0입니다.
앞으로 간혹 그냥 벡터(vector)라고 할 때에도 보통 4-벡터(four-vectors)를, 기저벡터(basis vectors)는 기저 4-벡터(basis four-vectors)를 가르키는 것으로 간주하시기 바랍니다.
𝐚 = at𝐞t + ax𝐞x + ay𝐞y + az𝐞z <5-1> <- '𝐚'와 같이 굵은 글자(boldface letters)는 벡터, '𝐞'는 기저벡터(basis vectors).
𝐚 = a0𝐞0 + a1𝐞1 + a2𝐞2 + a3𝐞3 <5-2>
∑3α=0 aα𝐞α <5-3> <- 아래와 같이 Einstein summation convention(아인슈타인 합산 규약)으로 표기 가능
𝐚 = aα𝐞α <5-4> <- Greek indices: 0~3 합산, Roman indices: 1~3 합산 [Hartle책의 경우, Landau-Lifshitz책에서는 반대임.]
at'= γ(at - Vax/c2), ax'= γ(ax - Vat/c2), ay'= ay, az'= az, γ = (1 - V2/c2)-1/2 <5-9> <- Lorentz Boost of a Vector)
𝐚 ∙ 𝐛 = (aα𝐞α) ∙ (bβ𝐞β) = (𝐞α ∙ 𝐞β) aα bβ <5-11>
ηαβ ≡ 𝐞α ∙ 𝐞β <5-13>
𝐚 ∙ 𝐛 = ηαβ aα bβ <5-5>
(Δs) ² = Δ𝑥 ∙ Δ𝑥 <5-14>
┃-1 0 0 0 ┃
ηαβ = ┃ 0 1 0 0 ┃ <5-15> <- 평평한 시공간의 계량(Mertic of Flat Spacetime)
┃ 0 0 1 0 ┃
┃ 0 0 0 1 ┃
ds2 = ηαβdxα dxβ <5-16>
𝐚 ∙ 𝐛 = -at bt + ax bx + ay by + az bz <5-17a>
𝐚 ∙ 𝐛 = -a0 b0 + a1 b1 + a2 b2 + a3 b3 <5-17b>
참고로, Landau-Lifshitz § 6. Four-vectors 에서는 Hartle책과 달리 4-vector의 두 type의 요소들(elements)을 도입합니다.
x0 = ct, x1 = x, x2 = y, x3 = z -> ds² = (x0)2 - (x1)2 - (x2)2 - (x3)2. <- Landau-Lifshitz책은 timelike interval을 사용.
𝐴0 = γ(𝐴'0 + V/c𝐴'1), 𝐴1 = γ(𝐴'1 + V/c𝐴'0), 𝐴2 = 𝐴'2, 𝐴3 = 𝐴'3 (6.1) <- <5-9>와 같은 벡터의 로렌츠 부스트인데 관성계 순서가 다른 식임.
(radius of 𝐴)2 ⇒ (𝐴0)2 - (𝐴1)2 - (𝐴2)2 - (𝐴3)2. 여기서 𝐴𝑖 contravariant element(반변 요소)와 𝐴𝑖 covariant element(공변 요소)를 도입합니다.
𝐴0= 𝐴0, 𝐴1= -𝐴1, 𝐴2= -𝐴2, 𝐴3= -𝐴3 (6.2)
𝐴𝑖𝐴𝑖 = 𝐴0𝐴0 + 𝐴1𝐴1 + 𝐴2𝐴2 + 𝐴3𝐴3.
𝐴𝑖𝛣𝑖 = 𝐴0𝛣0 + 𝐴1𝛣1 + 𝐴2𝛣2 + 𝐴3𝛣3. <- 𝐴𝑖𝛣𝑖: 4-scala, 관성계간에서 불변하는 양.
5.2 특수상대성 운동학(Special Relativistic Kinematics)
위 두번째 그림은 단순히 가속된(simple accelerated)의 세계선의 예로서 고유시간 𝜏로서 매개변수적으로 표시된 세계선을 보여줍니다. [화살표 𝐮는 아래의 4-velocity)]
xα = xα(τ) <- 𝜏: 고유시간(proper time) <5-21>
t(σ) = a-1sinh(σ), x(σ) = a-1cosh(σ) <5-22>
dτ2 = -ds2 = dt2 - dx² = [a-1cosh(σ)dσ]2 - [a-1sinh(σ)dσ]2 = (a-1dσ)2 <5-23> <- cosh2(σ) - sinh2(σ) = 1
t(τ) = a-1sinh(aτ), x(τ) = a-1cosh(aτ) <5-24>
위 세번째 그림은 앞에서 말한 입자의 세계선(particle's worldline)의 곡선에서 두번째 그림에서와 마찬가지로 접선벡터(tangent vector 𝐮를 보여주고 있습니다.
uα = dxα /d𝜏 <5-25> <- 𝐮: 4-velocity)
ut = dt/d𝜏 = 1 / √ (1 - V2/c2) = γ <5-26>
ux = dx/d𝜏 = dx/dt dt/d𝜏 = 𝑉x / √ (1 - V2/c2) = γ 𝑉x <5-27>
uα = (γc, γ𝑉) = γ(c, 𝑉) <5-28> <- 𝑉 = (𝑉x, 𝑉y, 𝑉z): 입자의 3-velocity
𝐮 ∙ 𝐮 = -1 [Normalization of four-velocity] <5-29> <- 4-vector의 normalization(규격화)
왜냐하면 𝐮 ∙ 𝐮 = -γ2 + (γ/c)2 V2 = -1/(1- V2/c2) + V2/[c2(1- V2/c2)] = - (1 - V2/c2)/(1 - V2/c2) = -1
𝐮 ∙ 𝐮 = ηαβ [dxα /d𝜏] [dxβ /d𝜏] = -1 <5-30>
참고로, Landau-Lifshitz § 7 Four-dimensional velocity 에서는 𝐮𝑖 ∙ 𝐮𝑖 = 1 (7.3). <- Landau-Lifshitz책은 timelike interval을 사용
5.3 특수상대성 동력학(Special Relativistic Dynamics)
<운동 방정식(Equation of Motion)>
d𝐮/d𝜏 = 0 <5-34> <- Newton's First Law(뉴톤의 제1법칙) ∵ <5-22>에서 V가 등속임으로
𝐚 ≡ d𝐮/d𝜏 <5-36> <- 𝐚: four-acceleration
𝐟 = 𝑚 d𝐮/d𝜏 <5-37> <- Newton's Second Law(뉴톤의 제2법칙)
𝐟 ∙ 𝐮 = 0 <5-39> <- d(𝐮 ∙ 𝐮) /d𝜏 = 0, 𝐮 ∙ 𝐚 = 0.
위 두번째 그림에서 가속도의 크기(the magnitude of acceleration):
(𝐚 ∙ 𝐚)1/2 = a <5-30> <- at ≡ dut/d𝜏 = a sinh(a𝜏), ax ≡ dux/d𝜏 = a cosh(a𝜏), cosh2(aτ) - sinh2(aτ) = 1.
<에너지-운동량(Energy-Momentum)>
𝐏 = 𝑚0 𝐮 = 𝑚0γ(c, 𝑉) = (-𝑚c, 𝑝) <5-41> <- 𝐏: 4-monentum
d𝐏/dτ = 𝐟 <5-42>
𝐏2 ≡ 𝐏 ∙ 𝐏 = -𝑚2c2 + 𝑝2 <5-43>
pt = 𝑚γc, 𝑝 = 𝑚γ𝑉 <5-44>
pt = 𝑚c2 + 1/2 𝑚𝑉2 + ..., 𝑃 = 𝑚𝑉 + ... <5-45>
왜냐하면 빛의 속도보다 아주 느릴 때, 𝑉 ≪ 1, γ의 테일러 급수(Tayler's series): (1+x)-1/2 = 1 - 1/2x + 3/8 x2 - ..., [x = -𝑉2/c2]
pα = (pt, 𝑃) = (𝑚γc, 𝑚γ𝑉) <5-46> <- 𝐸: 에너지(energy) 𝐸 ≡ ptc = 𝑚γc2 *
𝐸 = 𝑚c2 [when 𝑝 = 0] <5-47> <- in MLT system, when particle is at rest. 'The Most Famous Equation in Relativity or Physics'
𝐸 = (𝑚2c4 + 𝑝2c2)1/2 <5-48>
d𝑃 /dt ≡ 𝐹 <5-49> <- 𝐹: 3-force), Newton's Third Law(뉴톤의 제3법칙)
𝐟 = (γ 𝐹 ∙ 𝑉, γ 𝐹) <5-40> <- d𝑃/dτ = (d𝑃/dt) (dt /dτ) = 𝐹 γ.
d𝐸 /dt = 𝐹 ∙ 𝑉 <5-41>
요약한다면, 뉴톤 역학(Newtonian mechanics)은 특수상대성 역학(Special relativistc mechanics)의 낮은 속도에서의 근사인 것입니다.
※ 참고로, 나중에 상대론적 양자역학에서 아주 유용하게 쓰일 에너지와 운동량과의 관계식을 정리하면
𝐏2 = 𝑚02c2 = 𝑚2c2 - 𝑝 2 (S1) <- 특수상대성에 의한 불변량(invariant) 𝐏2, 𝑚0: 정지상태의 질량
그리고 𝐸 = 𝑚c2 라는 사실을 이용하면 다음을 얻습니다.
𝐸2 = 𝑝2c2 + 𝑚02c4, 𝑝2 = c2(𝑚2 - 𝑚02) (S2)
* 에너지 관계식 유도 (학부용 교재 A. Beiser Concepts of Modern Physics 6th edition McGraw-Hil 2003 pp. 26-27)
KE = ∫0s 𝐟 ds
KE = ∫0s d(γ𝑚𝑉)/dt ds = ∫0𝑉 𝑉 d(γ𝑚𝑉) = ∫0𝑉 𝑉 d(𝑚𝑉/√(1 - V2/c2)
이 부분적분 공식 (∫ x dy = xy - ∫ y dx) 을 이용해서 정리하면, [γ = 1/√(1 - V2/c2)]
KE = 𝑚c2/√(1 - V2/c2) - 𝑚c2 = (γ - 1)𝑚c2
이 결과는 한 물체의 운동에너지 KE는 γ𝑚c2와 𝑚c2의 차이를 가르키므로 전체에너지 𝐸는
𝐸 = γ𝑚c2 = 𝑚c2 + KE = 𝐸0 + KE 따라서 정지한 물체의 에너지 𝐸0
𝐸0 = 𝑚c2, 𝐸 = 𝑚c2/√(1 - V2/c2)
추가로 대학원 수준의 Landau-Lifshitz의 라그랑지안(Lagrangian)을 사용한 추론은 [§ 8 참조]
𝑆 = -𝛼 ∫ab ds <- 최소작용의 원리(principle of least action)
𝑆 = ∫t1t2 𝐿 dt <- 𝐿: 리그랑지언(Lagrange function)
ds2 = c2dt'2 = c2dt2 - dx2 - dy2 - dz2
ds = cdt' = cdt√[1 - (dx2 + dy2 + dz2)/c2dt2] = cdt√(1 - v2/c2)
그러므로 𝐿 = -𝛼c√(1 - v2/c2) ≈ -𝛼c + 𝛼v2/2c <- 테일러 급수 사용
이를 고전역학적 표현 𝐿 = 𝑚v2/2 과 비교함으로써 𝛼 = 𝑚c 를 구합니다. 그러므로,
𝐿 = -𝑚c2√(1 - v2/c2) ≈ -𝑚c2 + 𝑚v2/2 <- 𝐿 = KE - PE PE: 퍼텐셜에너지
에너지 𝐸 = 𝐏 • v - 𝐿 (𝐏 • v = 2KE) 이므로 𝐸 = 𝑚c2/√(1 - v2/c2) ≈ 𝑚c2 + 𝑚v2/2
따라서, v = 0 일 때 𝐸0 = 𝑚c2 ∎
참고문헌 Landau, L.D.; Lifshitz, E.M. (1980)[1939] The Classical Theory of Fields (4th ed.) Butterworth-Heinemann
Hartle, J.B. (2003) Gravity: An Introduction to Einstein’s General Relativity, Addison-Wesley |
|
|





































