|
김관석
|
2018-07-05 06:34:56, 조회수 : 980 |
- Download #1 : SR4.jpg (84.5 KB), Download : 1

5.4 자유입자 운동의 변분 원리(Variational Principle for Free Particle Motion)
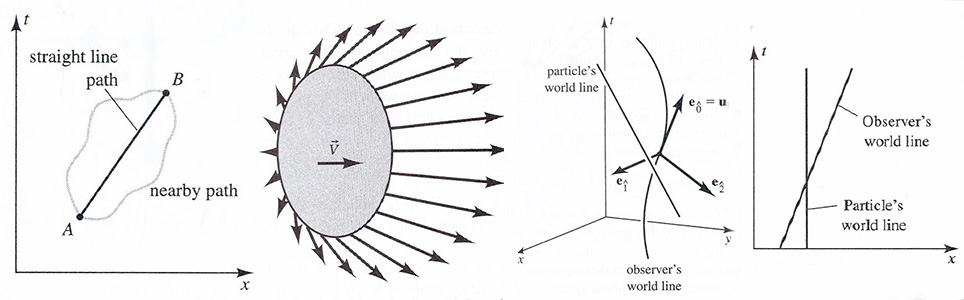
첫번째 그림은 시간성으로 분리된(timelike seperated) 두 점들 사이를 움직이는 자유입자의 세계선은 그들 사이의 고유시간(proper time)을 극치화한다(extremize)는 것입니다.
뉴톤 역학의 법칙은 극치화된 작용의 원리(the principle of extremal action)로 불리우는 변분 원리(variational principle)로서 공식화 되는데, 상대론적 역학에서도 같은 방식이 적용됩니다.
잘 이해해야 하는데, 그 과정은 먼저 고유시간의 식을 작성한 다음에 그 식을 오일러-라그랑주 방정식(Euler-Lagrange equatuion)을 이용해 운동 방정식(motion eqation)을 찾으면 됩니다.
τAB = ∫(from A to B) dτ = ∫(from A to B) [dt² - dx² - dy² -dz²]1/2 <5-42>
τAB = ∫(from A to B) dσ = [(dt/dσ)² - (dx/dσ)²- (dy/dσ)² - (dz/dσ)²]1/2 <5-43> <- σ = 0 at A point, σ = 1 at B point
d(∂𝐹/∂𝑦')/d𝑥 - ∂𝐹/∂𝑦 = 0 [오일러-라그랑주 방정식(Euler-Lagrange equatuion)] <5-44> <- 𝐹(𝑥, 𝑦, 𝑦') 함수의 극치화(exremization), 상세한 내용과 증명은 위키백과를 참조
𝐹 ↦ L = [(dt/dσ)² - (dx/dσ)²- (dy/dσ)² - (dz/dσ)²]1/2, 𝑥 ↦ σ, 𝑦 ↦ xα, 𝑦' ↦ dxα/dσ <5-45>
d(∂L/∂dxα/dσ)/d𝑥 - ∂L/∂xα = 0, ∂L/∂xα = 0, d(∂L/∂dxα/dσ)/d𝑥 = 0 <5-46> <- ∵ L은 xα와 독립적(independant)이므로
d(∂L/∂dxα/dσ)/d𝑥, L ↦ √ (dxα/dσ)², d[(1/L) * (dxα/ dσ)] = 0 <5-47> <- m ↦ dxα/dσ, d[(1/2 √ m²) * m²/dσ]/dσ, d[(1/2 √ m²) * 2m * (dm/dσ)]/dσ
d²xα/dτ² = 0 [AB사이의 직선 세계선(Straight world line between A and B)] <5-48> <- L = dτ/dσ 이므로, 양변에 (dσ/dτ)² 를 곱하여 dσ를 소거함.
즉, 자유입자의 평평한 시공간에서의 세계선은 고유시간을 극치화한 곡선인 것입니다. (이를 관성 좌표계의 시공간에서의 측지선-geodesic-이라 부를 수 있습니다.)
5.5 광선(Light Rays)
정지 질량 제로 입자들(Zero Rest Mass Particles)
정지 잘량이 없고 𝑉 = 1인 광속으로 움직이는 입자에 대해 생각해 본다면, 빛의 양자(quanta of light)와 중력(gravity)-광자(photons), 중력자(gravitons)와 몇몇 중성미자(nutrinos)가 예입니다.
여기서는 비양자적인 양상(nom-quatum aspects)에서의 광선(light rays)이라고도 불리우는 광자들(photons)에 대해서만 촛점을 맞추지만 광속으로 움직이는 다른 입자들에도 적용됩니다.
𝑥 = 𝑡, 𝑉 = 1, τ(proper time) = -√ ds² = 0 <5-48> <- ∴ 고유시간 τ이 0이라서 매개변수(parameter)로 사용할 수 없음.
𝑥α = 𝑢α λ <5-49> <- λ 는 다른 매개변수(parameter), 𝑢α = (1,1,0,0) [t = 1, x = 1]
𝐮 ∙ 𝐮 = 0 <5-50> <- ∵ 접선벡터(tangent vector) 𝐮 의 요소인 𝑢α = d𝑥α/ dλ 인데, 𝐮 는 널 벡터(null vector)이므로
d𝐮 /dλ = 0 <5-51> <- 광선(light ray)의 움직임의 방정식, 입자의 운동 방정식인 <5-26> d𝐮/dτ = 0 과 유사함..
여기의 광선에 대한 운동 방정식에 사용되는 매개변수 λ 는 입자를 위한 매개변수와 같은 것으로서 아핀 매개변수(affine parameters)라고 부릅니다.
에너지, 운동량, 주파수 그리고 파동 벡터(Energy, Momentum, Frequency and Wave Vector)
광자(photons)와 중성미자(neutrinos)는 에너지와 3-운동량(three momentum)을 가집니다. 플랑크-아인슈타인 관계식에 의해서 각 관성계에서 의 광자에너지 𝐸 는 각진동수 ω 와 연관됩니다.
𝐸 = h 𝑣 = ħ ω [Planck-Einstein relations] <5-52> <- h: 플랑크 상수, 𝑣: 주파수, ħ: 디랙 상수(Dirac's constant), ω: 각진동수(angular frequency), 𝑣 = ω/2π, ħ = h/2π
𝑃 = ħ 𝐾 <5-53> <- <5-36>에서 𝑃 = 𝐸 𝑽, ∣𝑽∣ = 1, ∴ ∣𝑃∣ = 𝐸, 𝐾: 파동 3-벡터(wave three vector), ∣𝐾∣ = ω,
pα = (𝐸, 𝑃) = (ħ ω, ħ 𝐾 ) = ħ kα <5-54> <- 𝐤: 파동 4-벡터(wave four vector)
𝐩 ∙ 𝐩 = 𝐤 ∙ 𝐤 = 0 <5-55>
d𝐩 /dλ = 0, d𝐤 /dλ = 0 <5-56> <- λ: 아핀 매개변수(affine parameter)
광자(photons)는 0 의 정지 질량을 갖고, 4-벡터 𝐩, 𝐤 는 널(null) 세계선의 접하며, 접선벡터 𝐮 는 아핀 매객변수 λ 의 규격화(normalization)를 조정함으로써 𝐩, 𝐤 와 일치시킬 수 있게 됩니다.
도플러 편이와 상대론적 비밍[분사출](Doppler shift and Relativistic Beaming)
사방으로 ω 의 (각)진동수로 광자를 분출하고 있는 광원이 있는 계와 이와 x'축 방향으로 속도 V로 움직이는 관성계를 생각해보면 역시 로렌츠 부스트(Lorentz Boost)로서 관계식이 성립합니다.
이 경우에 x'축과 α'의 각도를 이루는 한 광자(a phonton)의 진동수(주파수 frequency)는 어떠할까를 살펴보기로 합시다.
ω = γ (ω' - V kx' ) <5-57> <- <5-54>에 따라 파동 4-벡터 𝐤 의 kα = (ω, 𝐾), k'α = (ω', 𝐾') 라고 하면
ω' = ω √ (1 - V²) / (1- V cos α') <5-58> <- 상대론적 도플러 편이(Relativistic Doppler Shift}
ω' ≈ ω (1 + V cos α') <5-59> <- V가 작을 때, 1/(1 - x) = 1 + x + x² + ..., (∣x∣<1), 매클로린 급수(Maclaurin series)
α'= 0 이면 Δω = + V ω 이므로 청색편이(blue shift)이, α'= π 이면 Δω = - V ω 이므로 적색편이(red shift)이, α'= π/2 이면 <5-58>에 따라 횡단 적색편이(tansverse red shift)가 됩니다!
위의 두번째 그림은 V = 0.75c 의 상대론적 비밍 현상을 보여줍니다. 원래는 같은 길이인 화살표의 벡터들이 도플러 효과때문에 짧아지고(적색편이), 길어지며(청색편이), 각각 방향들도 변화합니다.
cos α'= (cos α + V) / (1 + V cos α) <5-60> <- x(x')축과 α(α')의 각도를 이루며 방출되는 광자의 cos α = kx/ ω, cos α' = kx'/ ω', 로렌츠 변환(Lorentz Transformation)됨.
균일하게 빛을 내는 물체가 우리에게 다가올 때가 멀어질 때보다 도플러 효과에 의해 강도(intencity)가 더 집중되어 더 밝게 보이는 것을 상대론적 비밍(Relativistic Beaming)*이라 부릅니다.
5.6 관찰자와 관측(Observers and Observations)
위의 세번째 그림에서 가속되고 있는 세계선의 한 지점(world point)에서 국소 실험실(local laboratory)로서 직교하는 시간 차원과 3방향의 공간 차원의 𝐞𝟘, 𝐞𝟙, 𝐞𝟚, 𝐞𝟛 기저 4-벡터를 갖습니다.
𝐞𝟘 = 𝐮obs <5-61> <- 𝐮obs: 관측자의 4-속도 벡터(Observer's four-velocity vector), 세계점에서의 단위 접선벡터(unit tangent vector at world point)
𝐩 = pα𝐞α <5-62>
p𝟘 = -𝐩 ∙ 𝐞𝟘, p𝟙 = 𝐩 ∙ 𝐞𝟙, p𝟚 = 𝐩 ∙ 𝐞𝟚, p𝟛 = 𝐩 ∙ 𝐞𝟛 <5-63> <- 기저 벡터들은 상호간 직교(orthoonal)하므로 점곱(dot product)을 하면 스스로의 요소만이 남음.
위의 네번째 그림은 한 입자가 그대로 정지해 있으면서(at rest) 관측자는 속도 V로 움직일 때, 관측자의 4-속도 벡터를 따라 4-운동량 중의 입자의 에너지(energy)를 측정하는 경우의 도해입니다.
𝐩 = (m, 0, 0, 0) <5-63> <- m: 정지 질량(rest mass)
𝐞𝟘 = 𝐮obs = (γ, Vγ, 0, 0) <5-64>
𝐸 = -𝐩 ∙ 𝐞𝟘 = -𝐩 ∙ 𝐮obs = m γ <5-65>
즉, 움직이는 관찰자가 측정한 정지한 입자의 에너지는 결국 관측자의 시간축 기저벡터 𝐞𝟘를 따르는 그 입자의 에너지-운동량 4-벡터(energy- momentum 4-vector)의 요소인 것입니다..
참고문헌 Landau, L.D.; Lifshitz, E.M. (1980)[1939] The Classical Theory of Fields (4th ed.) Butterworth-Heinemann
Hartle, J.B. (2003) Gravity: An Introduction to Einstein’s General Relativity, Addison-Wesley
p.s. 특수상대성의 수학은 기초 수준이므로 '개념'을 잘 파악하면 되지만, 일반상대성은 '고등 수학'-미분기하학과 텐서해석을 바탕으로 한다고 ...
여기서는 측지선을 찾는 변분법의 '오일러-라그랑주 방정식'이 가장 높은 난이도를 지닌 수리물리학이므로 별도의 학습이 필요함.
* 초급 영어인 beaming을 전공자만 알 수 있는 '분사출(噴射出)'로 번역해서 기억하는 것은 넌센스인 듯해서 발음대로 표기함. |
|
|





































