로그인 회원가입

텐서 해석 II-2. 좌표변환 II; 일반 좌표계 미분

김관석	2019-06-03 23:41:00, 조회수 : 1,398

- Download #1 : Tensor_II_2.jpg (55.1 KB), Download : 1

II-3 좌표의 변환 II

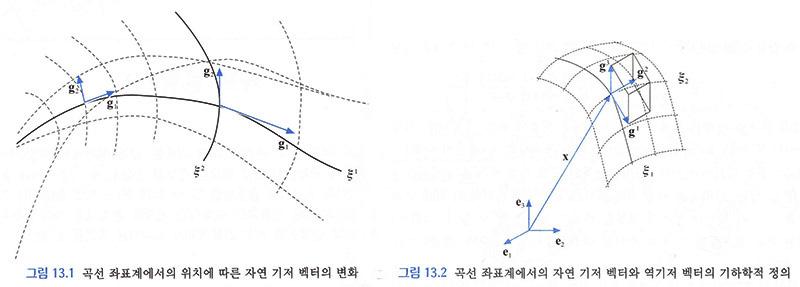
      a) 13.1,2 Basis(기저) vector의 수학적 유도   <- 그림 13.1, 13. 2 참조
        ∘ R³ 공간에서 점 P는 Cartesian 좌표계에서는 (𝑥¹, 𝑥², 𝑥³), 일반 좌표계에서는 (𝜉¹, 𝜉², 𝜉³) 로 표기할 수 있습니다.
          두 좌표계 사이에 서로 변환이 가능하다고 할 때 그 관계식은  𝑥^𝑖 =  𝑥^𝑖(𝜉¹, 𝜉², 𝜉³),  𝜉^𝑖 =  𝜉^𝑖(𝑥¹,  𝑥², 𝑥³)가 됩니다.    [13.1.1,2]
          따라서, 점 P의 기준점으로부터의 위치 vector는 𝐱 = 𝐱(𝜉¹, 𝜉², 𝜉³)로 표기할 수 있습니다.   [13.1.3]
        ∘ natural basis(자연 기저) vector의 정의: 𝐠_𝑖 ≡ ∂𝐱/∂𝜉^𝑖 <- 한 점에서 각 좌표 방향으로의 tangent(접선)의 성질   [13.2.1]
          점 P는 Cartian 좌표계로 𝐱 = 𝑥¹𝐞₁+ 𝑥²𝐞₂+ 𝑥³𝐞₃= 𝑥^𝑖 𝐞_𝑖,  ∴ 𝐠_𝑖 = ∂𝐱/∂𝜉^𝑖 = (∂𝑥^𝑗/∂ξ^𝑖) 𝐞_𝑗   [13.2.5]
           ex) 원통 좌표계 (𝜉¹ = 𝑟, 𝜉² = 𝜃, 𝜉³ = 𝑧)에서의 자연 기저 vector 𝐠_𝑖를 구하시오.  ◂
              𝑥¹ =  𝜉¹cos 𝜉²,  𝑥² =  𝜉¹sin 𝜉²,  𝑥³ = 𝜉³      [13.2.6]
              𝐠₁ = ∂𝑥¹/∂𝜉¹𝐞₁ + ∂𝑥²/∂𝜉¹ 𝐞₂ + ∂𝑥³/∂𝜉¹ 𝐞₃ = cos𝜉² 𝐞₁ + sin𝜉² 𝐞₂ = cos𝜃 𝐞₁ + sin𝜃 𝐞₂
              𝐠₂ = ∂𝑥¹/∂𝜉²𝐞₁ + ∂𝑥²/∂𝜉² 𝐞₂ + ∂𝑥³/∂𝜉² 𝐞₃ = -𝜉¹ sin𝜉² 𝐞₁ + 𝜉¹ cos𝜉² 𝐞₂ =  -𝑟 sin𝜃 𝐞₁ + 𝑟 cos𝜃 𝐞₂   [13.2.7]
              𝐠₃ = ∂𝑥¹/∂𝜉³𝐞₁ + ∂𝑥²/∂𝜉³ 𝐞₂ + ∂𝑥³/∂𝜉³ 𝐞₃ = 𝐞₃  ▮
        ∘ reciprocal basis(역기저) vector의 정의: 𝐠^𝑖 ≡ ∂𝜉^𝑖/∂𝐱 <- 한 점에서 각 좌표 방향으로의 normal(법선)의 성질   [13.2.2]
           𝐠^𝑖 ≡ ∂𝜉^𝑖/∂𝐱 = (∂𝜉^𝑖/∂𝑥^𝑗) 𝐞^𝑗  <- 𝐠^𝑗 ∙ 𝐠_𝑖 = 𝛿^𝑗_𝑖,  ※ natural basis vector와 reciprocal basis vector는 상호 직교함
        ∘ 𝐞_𝑖 = (∂𝜉^𝑗/∂𝑥^𝑖) 𝐠_𝑗,  𝐞^𝑖 = (∂𝑥^𝑗/∂𝜉^𝑖) 𝐠^𝑗  <- Cartesian 좌표계는 contaravariant(반변)과 covariant(공변)의 구분이 없으므로  𝐞_𝑖 = 𝐞^𝑖   [13.2.3,4]
      b) 13.3 Metric tensor의 의미
        ∘ Cartesian 좌표계에서: metric tensor: 𝛿_𝑖_𝑗
          𝐱 = 𝑥¹𝐞₁+ 𝑥²𝐞₂+ 𝑥³𝐞₃= 𝑥^𝑖 𝐞_𝑖   𝑑𝐱 = 𝑑𝑥¹𝐞₁+ 𝑑𝑥²𝐞₂+ 𝑑𝑥³𝐞₃= 𝑑𝑥^𝑖 𝐞_𝑖   𝑑𝑠² = 𝑑𝐱 ∙ 𝑑𝐱 = 𝑑𝑥^𝑖 ∙ 𝑑𝑥^𝑗 = 𝑑𝑥^𝑖𝑑𝑥^𝑗 𝛿_𝑖_𝑗 = 𝑑𝑥^𝑖𝑑𝑥^𝑖,  ∴ 𝑑𝑠² ≡ 𝑑𝑥^𝑖𝑑𝑥^𝑖   [13.3.1-7]
        ∘ General(일반) 좌표계에서: metric tensor: 𝑔_𝑖𝑗 = 𝐠_𝑖 ∙ 𝐠_𝑗
          𝑑𝐱 = (∂𝐱/∂𝜉^𝑖)𝑑𝜉^𝑖   𝑑𝐱 = 𝐠_𝑖 𝑑𝜉^𝑖   𝑑𝑠² = 𝑑𝐱 ∙ 𝑑𝐱 =  𝑑𝜉^𝑖 𝐠_𝑖 ∙ 𝑑𝜉^𝑗 𝐠_𝑗  = 𝑔_𝑖𝑗 𝑑𝜉^𝑖𝑑𝜉^𝑗 ∴ 𝑑𝑠² ≡ 𝑔_𝑖𝑗 𝑑𝜉^𝑖𝑑𝜉^𝑗   [13.3.8-10]
      c) 13.4 좌표 변환의 조건
        ∘ Jacobian이 0(zero)이 아님
          Cartesian 좌표계의 (𝑥¹, 𝑥², 𝑥³)에서 일반 좌표계의 (𝜉¹, 𝜉², 𝜉³)로의 변환 Jacobian 𝐽 는 아래처럼 정의하며, 그 변환 조건은
          𝐽 ≡ det (∂𝑥^𝑗/∂𝜉^𝑖) =
             ∣ ∂𝑥¹/∂𝜉¹  ∂𝑥¹/∂𝜉²  ∂𝑥¹/∂𝜉³ ∣
             ∣ ∂𝑥²/∂𝜉¹  ∂𝑥²/∂𝜉²  ∂𝑥²/∂𝜉³ ∣  ≠ 0   [13.4.1]
             ∣ ∂𝑥 ³/∂𝜉¹ ∂𝑥³/∂𝜉²  ∂𝑥³/∂𝜉³ ∣
             𝐽 =  𝜖_𝑖𝑗𝑘 (∂𝑥^𝑖/∂𝜉¹)(∂𝑥^𝑗/∂𝜉²)(∂𝑥^𝑘/∂𝜉³) = (∂𝐱/∂𝜉¹) ⨯ (∂𝐱/∂𝜉²) ∙ (∂𝐱/∂𝜉³) = 𝐠₁ ⨯ 𝐠₂ ∙ 𝐠₃ = 𝜖_𝑖𝑗𝑘 = √ 𝑔  <- g = det [g_𝑖𝑗]      [13.3.1-7]
            𝐽  > 0 : 오른손 법칙의 좌표계로의 변환,  𝐽  < 0 : 왼손 법칙의 좌표계로의 변환,   𝐽 = 0   변환 불가     [13.4.8]
     d) 13.5 Tensor의 좌표 변환  <- 하나의 일반 좌표계 𝜀^𝑖에서 다른 일반 좌표계 𝜀̄^𝑖으로의 변환
           각각의 natural basis(자연 기저) vector 𝐠_𝑖 = ∂𝐱/∂𝜀^𝑖, 𝐠̄_𝑖 = ∂𝐱/∂𝜀̄^𝑖들의 dot product(내적)를 변환 tensor로 정의합니다.   [13.5.1]
        ∘ 변환 tensor 𝑙_𝑖𝑗 ≡ 𝐠̄_𝑖 ∙ 𝐠_𝑗 = ∂𝐱/∂𝜀̄^𝑖 ∙ ∂𝐱/∂𝜀^𝑗 = (∂𝜀^𝑘/∂𝜀̄^𝑖)(∂𝐱/∂𝜀^𝑘) ∙ ∂𝐱/∂𝜀^𝑗 = (∂̄𝜀^𝑘/∂𝜀̄^𝑖) 𝐠_𝑘 ∙ 𝐠_𝑗 = 𝑔_𝑘𝑗 ∂̄𝜀^𝑘/∂𝜀̄^𝑖  <- chain rule 적용   [13.5.2-5]
        ∘ 𝑢̄_𝑖 = 𝑙_𝑖𝑗 𝑢^𝑗,  𝑢̄_𝑖 = 𝑙_𝑖.^𝑗 𝑢_𝑗,  𝑢̄ ^𝑖 = 𝑙^𝑖_.𝑗 𝑢^𝑗,  𝑢̄ ^𝑖 = 𝑙^𝑖𝑗 𝑢_𝑗  <- 변환 tensor는 contravariant 성분 ⇄ covariant 성분 역할   [13.5.5-9]
        ∘ 𝑙_𝑖𝑗 =  𝑔_𝑘𝑗 ∂̄𝜀_𝑘/∂𝜀̄^𝑖 = 𝑔̄_𝑖𝑘 ∂̄𝜀̄_𝑘/∂𝜀^𝑗,  𝑙^𝑖𝑗 =  𝑔̄_𝑘𝑖 ∂̄𝜀̄_𝑘/∂𝜀^𝑗 = 𝑔_𝑘𝑗 ∂̄𝜀_𝑘/∂̄𝜀̄ ^𝑖,   𝑙^𝑖_.𝑗 =  ∂̄𝜀̄^𝑖/∂𝜀^𝑗,   𝑙_𝑖.^𝑗 =  ∂𝜀^𝑗/∂𝜀̄ ^𝑖   [13.5.10-13]
           ex) 𝑙^𝑖_.𝑗 유도 →  𝑙^𝑖_.𝑗 = 𝐠̄^𝑖 ∙ 𝐠_𝑗 = 𝑔̄^𝑖𝑘 𝐠̄_𝑘 ∙ 𝐠_𝑗 = 𝑔̄^𝑖𝑘 ∂𝐱/∂𝜀̄^𝑘 ∙ ∂𝐱/∂𝜀^𝑗 = 𝑔̄^𝑖𝑘 ∂𝐱/∂𝜀̄^𝑘 ∙ (∂𝜀̄^𝑙/∂𝜀̄^𝑙)∂𝐱/∂𝜀^𝑗 = 𝑔̄^𝑖𝑘 ∂𝐱/∂𝜀̄^𝑘 ∙ (∂𝜀̄^𝑙/∂𝜀^𝑗)∂𝐱/∂𝜀̄^𝑙
                                              = 𝑔̄^𝑖𝑘 𝐠̄_𝑘 ∙ (∂𝜀̄^𝑙/∂𝜀^𝑗)𝐠̄_𝑙 = 𝐠̄^𝑖 ∙ (∂𝜀̄^𝑙/∂𝜀^𝑗)   𝑙^𝑖_.𝑗 = 𝛿^𝑖_𝑙 ∂𝜀̄^𝑙/∂𝜀^𝑗 = ∂𝜀̄^𝑖/∂𝜀^𝑗    [13.5.16-21]
      e) 13.6,7 좌표 변환과 tensor의 정의
           Tensor는 정해진 변환 법칙을 만족하는 물리량이라고 정의할 수 있습니다. <- tensor의 좌표 변환: 임의 좌표계 𝜀^𝑖 → 𝜀̄ ^𝑖
        ∘ contravariant(반변) 변환 법칙: 임의의 vector를 각각의 좌표계에서 고려하면,  𝐮 = 𝑢̄^𝑗 𝐠̄_𝑗 = 𝑢^𝑗 𝐠_𝑗   [13.6.1]
           𝑢̄^𝑗 (∂𝐱/∂𝜀̄^𝑗) = 𝑢^𝑗 (∂𝐱/∂𝜀^𝑗),  𝑢̄^𝑗 (∂𝐱/∂𝜀̄^𝑗)(∂𝜀̄^𝑖/∂𝐱) = 𝑢^𝑗(∂𝐱/∂𝜀^𝑗)(∂𝜀̄^𝑖/∂𝐱),  𝑢̄^𝑗 𝛿^𝑖_𝑗 = 𝑢^𝑗 (∂𝜀̄ ^𝑖/∂𝜀^𝑗)  ∴   𝑢̄^𝑖 = 𝑢^𝑗 (∂𝜀̄^𝑖/∂𝜀^𝑗)   [13.6.2-8]
           ex) velocity 𝑣^𝑖 = 𝑑𝜀^𝑖/𝑑𝑡 를 좌표계 𝜀̄^𝑗에서 관찰하면,  𝑣̄^𝑗 = 𝑑𝜀̄^𝑗/𝑑𝑡 =  (∂𝜀̄^𝑗/∂𝜀^𝑘)(∂𝜀^𝑘/𝑑𝑡) = (∂𝜀̄^𝑗/∂𝜀^𝑘) 𝑣^𝑘 ∴ 변환 법칙을 만족   [13.7.1-3]
        ∘ covariant(공변) 변환 법칙: 유사한 방식으로 유도 하면,  𝑢̄_𝑖 = 𝑢_𝑗 (∂𝜀^𝑗/∂𝜀̄^𝑖)   [13.6.9]
        ∘ scalar 불변의 법칙: scalar는 0차 tensor로 지수가 없으므로, 𝜙̄(𝜀̄) = 𝜙(𝜀)   [13.6.12]
        ∘ 2차 tensor의 변환 법칙; contravariant(반변) tensor: 𝐴̄^𝑖𝑗 =  𝐴^𝑘𝑙 (∂𝜀̄^𝑖/∂𝜀^𝑘)(∂𝜀̄^𝑗/∂𝜀^𝑙)   [13.6.15]
               covariant(공변) tensor: 𝐴̄_𝑖𝑗 =  𝐴_𝑘𝑙 (∂𝜀^𝑘/∂𝜀̄^𝑖)(∂𝜀^𝑙/∂𝜀̄^𝑗),   혼합 tensor: 𝐴̄ ^𝑖_.𝑗 =  𝐴^𝑘_.𝑗 (∂𝜀̄^𝑖/∂𝜀^𝑘)(∂𝜀^𝑙/∂𝜀̄^𝑗)   [13.6.16,17]
       f) 13.8 Physical component(물리적 성분)의 정의 <- 아래 𝑖̄𝑖̄, 𝑗̄𝑗̄: 중복 지수(dummy index) 미적용 표기임
         ∘ normalization of basis(기저의 정규화): 물리적 성분의 사용을 위해 Cartesian 좌표계의 단위 기저 vector로 변환함
            𝐞_𝑖 = 𝐠_𝑖/∥𝐠∥= 𝐠_𝑖/√ 𝑔_𝑖̄𝑖̄ or  𝐠_𝑖 = √ 𝑔_𝑖̄𝑖̄ 𝐞_𝑖 마찬가지로,  𝐞^𝑖 = 𝐠^𝑖/∥𝐠∥= 𝐠^𝑖/√ 𝑔^𝑖̄𝑖̄ or 𝐠^𝑖 = √ 𝑔^𝑖̄𝑖̄ 𝐞^𝑖   [13.8.3,4]
             ex) 원통 좌표계 (𝜉¹ = 𝑟, 𝜉² = 𝜃, 𝜉³ = 𝑧),  여기서 metric tensor 들은  𝑔₁₁ = 𝑔₃₃ = 1,  𝑔₂₂ = 𝑟²  나머지는 0 입니다.
                 𝐞₁ = 𝐠₁/√ 𝑔¹¹ = 𝐠₁,  𝐞₂ = 𝐠₂/√ 𝑔²² = 𝐠₂/𝑟,  𝐞₃ = 𝐠₃/√ 𝑔³³ = 𝐠₃,   ∴  𝐠₁ = 𝐞₁,  𝐠₂ = 𝑟𝐞₂,  𝐠₃ = 𝐞₃   [13.8.5,7]
         ∘ physical component(물리적 성분):  unit basis(단위 기저) vector로 변환했을 때의 성분으로 정의합니다.
            𝐯 = 𝑣^(𝑖) 𝐞_𝑖 = 𝑣_(𝑖) 𝐞^𝑖;  contravariant 물리적 성분: 𝑣^(𝑖) = 𝑣^𝑖 √ 𝑔_𝑖̄𝑖̄,  covariant 물리적 성분: 𝑣_(𝑖) = 𝑣_𝑖 √ 𝑔^𝑖̄𝑖̄   [13.8.13-21]
           2차 tensor의 물리적 성분: 𝐴^(𝑖𝑗) 𝐠_𝑖 ⊗  𝐠_𝑗 → contravariant: 𝐴^(𝑖𝑗) = 𝐴^𝑖𝑗 √ (𝑔_𝑖̄𝑖̄𝑔_𝑗̄𝑗̄),  covariant: 𝐴_(𝑖𝑗) = 𝐴_𝑖𝑗 √ (𝑔^𝑖̄𝑖̄𝑔^𝑗̄𝑗̄)   [13.8.24-27]
           composite: 𝐴^(𝑖)_(.𝑗) = 𝐴^𝑖_.𝑗 √ (𝑔_𝑖̄𝑖̄/𝑔_𝑗̄𝑗̄)  ∴ 𝐀 =  𝐴^(𝑖𝑗) 𝐞_𝑖 ⊗ 𝐞_𝑗 =  𝐴_(𝑖𝑗) 𝐞_𝑖 ⊗ 𝐞_𝑗 = 𝐴^(𝑖)_(.𝑗) 𝐞_𝑖 ⊗ 𝐞_𝑗   [13.8.28-30]

II-4 일반 좌표계에서의 미분

      a) 14.1 Scala의 미분: ∂𝜙/∂𝜉^𝑗 or 𝜙_.𝑗 <- 𝜙: scala field   [14.1.1]
           ex) Scala 장 𝜙(𝜉¹, 𝜉², 𝜉³) = (𝜉¹)² + cos (𝜉²) + 𝜉³의 좌표에 대한 미분을 구하시오  ◂
                 ∂𝜙/∂𝜉¹ = 2𝜉¹,   ∂𝜙/∂𝜉² = -sin(𝜉²),   ∂𝜙/∂𝜉³ = 1  ▮
      b) Vector의 미분  <- ※ 성분에 대한 미분과 변화하는 기저 vector에 대한 미분을 함께 함
        ∘ contravariant vector 미분: ∂𝐮/∂𝜉^𝑗 = (∂/∂𝜉^𝑗)𝑢^𝑖 𝐠_𝑗 = (∂𝑢^𝑖/∂𝜉^𝑗) 𝐠_𝑖 + 𝑢^𝑖 (∂𝐠_𝑖/∂𝜉^𝑗) = 𝑢^𝑖_.𝑗 𝐠_𝑖 +  𝑢^𝑖 𝐠_𝑖.𝑗   [14.2.1-3]
           𝐠_𝑖 ≡ ∂𝐱/∂𝜉^𝑖 = ∂𝑥^𝑗/∂𝜉^𝑖 𝐞_𝑗,  𝐞_𝑖 = ∂𝜉^𝑗/∂𝑥^𝑖 𝐠_𝑖 → 𝐠_𝑖.𝑗 = ∂(∂𝐱/∂𝜉 𝑖)/∂𝜉𝑗 = ∂𝐱²/∂𝜉^𝑖∂𝜉^𝑗,  𝐠_𝑖.𝑗 = 𝐠_𝑗,𝑖.,  𝐠_𝑖.𝑗 = ∂²𝐱/∂𝜉^𝑖∂𝜉^𝑗 = (∂²𝑥^𝑚/∂𝜉^𝑖∂𝜉^𝑗) 𝐞_𝑚   [14.2.4-7]
             = (∂²𝑥^𝑚/∂𝜉^𝑖∂𝜉^𝑗)(∂𝜉^𝑛/𝑥^𝑚) 𝐠_𝑛 = 𝜞^𝑛_𝑖𝑗 𝐠_𝑛  ∴ ∂𝐮/∂𝜉^𝑗 = (∂/∂𝜉^𝑗)𝑢^𝑖 𝐠_𝑗 = 𝑢^𝑖_.𝑗 𝐠_𝑖 +  𝑢^𝑖 𝐠_𝑖.𝑗 = 𝑢^𝑖_.𝑗 𝐠_𝑖 + 𝑢^𝑖 𝜞^𝑛_𝑖𝑗 𝐠_𝑛 =  𝑢^𝑖_.𝑗 𝐠_𝑖 + 𝑢^𝑘 𝜞^𝑖_𝑘𝑗 𝐠_𝑖   [14.2.8]
        ∘ 2종 Christoffel 기호의 정의 <- ※ 기저 vector의 접선 방향 성분 by the Gauss Formulas
             𝜞^𝑛_𝑖𝑗 ≡ (∂²𝑥^𝑚/∂𝜉^𝑖∂𝜉^𝑗)(∂𝜉^𝑛/∂𝑥^𝑚),  𝐠_𝑖.𝑗∙ 𝐠^𝑘 = 𝜞^𝑛_𝑖𝑗 𝐠_𝑛∙ 𝐠^𝑘 = 𝜞^𝑛_𝑖𝑗 𝛿^𝑘_𝑛 = 𝜞^𝑘_𝑖𝑗   𝐠_𝑖.𝑗∙ 𝐠^𝑘 = 𝜞^𝑘_𝑖𝑗,   ∴ 𝐠_𝑖.𝑗∙ 𝐠^𝑘 =  𝜞^𝑘_𝑖𝑗   [14.2.9-11]
        ∘ contravariant 성분의 covariant 미분: ∂𝐮/∂𝜉^𝑗 = 𝑢^𝑖_.𝑗 𝐠_𝑖+ 𝑢^𝑘 𝜞^𝑖_𝑘𝑗 𝐠_𝑖 = (𝑢^𝑖_.𝑗 + 𝑢^𝑘 𝜞^𝑖_𝑘𝑗) 𝐠_𝑖 = 𝑢^𝑖∣_𝑗 𝐠_𝑖,  𝑢^𝑖∣_𝑗 ≡ 𝑢^𝑖_.𝑗 + 𝑢^𝑘 𝜞^𝑖_𝑘𝑗    [14.2.12,13]
        ∘ natural basis(자연 기저) vector의 미분: ∂𝐠_𝑖/∂𝜉^𝑗 = 𝜞^𝑘_𝑖𝑗 𝐠_𝑘,  ※  𝜞^𝑘_𝑖𝑗 = 𝜞^𝑘_𝑗𝑖 ∵ 𝐠_𝑖.𝑗 =  𝐠_𝑗.𝑖
        ∘ covariant 성분 vector의 미분: ∂𝐮/∂𝜉^𝑗 = (∂/∂𝜉^𝑗)𝑢_𝑖 𝐠^𝑗 = (∂𝑢_𝑖/∂𝜉^𝑗) 𝐠^𝑖 + 𝑢_𝑖 (∂𝐠^𝑖/∂𝜉^𝑗) = 𝑢_𝑖.𝑗 𝐠^𝑖 +  𝑢_𝑖 𝐠^𝑖_.𝑗   [14.2.14]
             𝐠^𝑖∙ 𝐠_𝑗 = 𝛿^𝑖_𝑗,  양변 𝜉^𝑘로 미분,   𝐠^𝑖_.𝑘∙ 𝐠_𝑗 + 𝐠^𝑖∙ 𝐠_𝑗.𝑘 = 0,  𝐠^𝑖_.𝑘∙ 𝐠_𝑗 = - 𝐠^𝑖∙ 𝐠_𝑗.𝑘, 𝐠^𝑖∙ 𝐠_𝑗.𝑘 = 𝜞^𝑖_𝑗𝑘,  𝐠^𝑖_.𝑘∙ 𝐠_𝑗 = -𝜞^𝑖_𝑗𝑘,  (𝐠^𝑖_.𝑘∙ 𝐠_𝑗)𝐠^𝑘 = -𝜞^𝑖_𝑗𝑘𝐠^𝑘   [14.2.15-18]
             (𝐠^𝑖_.𝑘 ∙ 𝐠_𝑗) 𝐠^𝑘 = 𝐠^𝑖_.𝑘 𝐠^𝑘 ∙ 𝐠_𝑗 = 𝐠^𝑖_.𝑘𝛿^𝑘_𝑗 = 𝐠^𝑖_.𝑗 <- *;  𝐠^𝑖_.𝑗 = -𝜞^𝑖_𝑗𝑘𝐠^𝑘,  ∴ ∂𝐮/∂𝜉^𝑗 = (∂/∂𝜉^𝑗)𝑢_𝑖 𝐠^𝑗 = 𝑢_𝑖.𝑗 𝐠^𝑖 - 𝑢_𝑖 𝜞^𝑖_𝑗𝑘𝐠^𝑘 = 𝑢_𝑖.𝑗 𝐠^𝑖 - 𝑢_𝑘 𝜞^𝑖_𝑗𝑘𝐠^𝑖   [14.2.16-20]
        ∘ covariant 성분의 covariant 미분: ∂𝐮/∂𝜉^𝑗 = 𝑢_𝑖.𝑗 𝐠_𝑖 +  𝑢_𝑖 𝐠^𝑖_.𝑗 = 𝑢_𝑖.𝑗 𝐠_𝑖 - 𝑢_𝑖 𝜞^𝑖_𝑗𝑘 𝐠^𝑘 = (𝑢_𝑖.𝑗 - 𝑢_𝑘 𝜞^𝑘_𝑖𝑗)𝐠^𝑖, 𝑢_𝑖∣_𝑗 ≡ 𝑢_𝑖.𝑗 - 𝑢_𝑘 𝜞^𝑘_𝑖𝑗   [14.2.21,22]
        ∘ reciprocal basis(역기저) vector의 미분: ∂𝐠^𝑖/∂𝜉^𝑗 = -𝜞^𝑖_𝑗𝑘 𝐠_𝑘
        ∘ 𝑢_𝑖∣_𝑗 - 𝑢_𝑗∣_𝑖 = (𝑢_𝑖.𝑗 - 𝑢_𝑘 𝜞^𝑘_𝑖𝑗) - (𝑢_𝑗,𝑖 - 𝑢_𝑘 𝜞^𝑘_𝑗𝑖) = 𝑢_𝑖.𝑗 - 𝑢_𝑗,𝑖 <-  𝜞^𝑘_𝑖𝑗 = 𝜞^𝑘_𝑗𝑖,  ∴ 𝑢_𝑖∣_𝑗 - 𝑢_𝑗∣_𝑖 = 𝑢_𝑖.𝑗 - 𝑢_𝑗,𝑖  <- ※ 자주 사용하는 관계식   [14.2.23,24]
        ∘ covariant 성분과 contravariant 성분을 갖는 vector에 대한 미분 관계식: 𝑢 _𝑖∣_𝑗 =  𝑔_𝑖𝑘 𝑢^𝑘∣_𝑗  <- by metric tensor   [14.2.25]
     c) Christoffel 기호
        ∘ 1종 Christoffel 기호의 정의: metric tensor와 2종 Christoffel 기호의 곱
                𝐠_𝑖.𝑗 = 𝜞^𝑘_𝑖𝑗 𝐠_𝑘 = 𝑔_𝑘𝑙 𝜞^𝑘_𝑖𝑗 𝐠^𝑙 <- 𝐠_𝑘 → 𝐠^𝑙 by metric 𝑔_𝑘𝑙,   𝜞_𝑖𝑗𝑙 ≡ 𝑔_𝑘𝑙 𝜞^𝑘_𝑖𝑗   <- ※ [𝑖𝑗, 𝑙]로도 표기함   [14.3.1,2]
               ∴ 𝐠_𝑖.𝑗 = 𝜞^𝑘_𝑖𝑗 𝐠_𝑘 = 𝜞_𝑖𝑗𝑙 𝐠^𝑙 <- 기저 vector에 따름, 𝜞^𝑘_𝑖𝑗 𝐠_𝑘 ∙ 𝐠^𝑚 = 𝜞_𝑖𝑗𝑙 𝐠^𝑙 ∙ 𝐠^𝑚,  𝜞^𝑘_𝑖𝑗𝛿^𝑚_𝑘 = 𝜞^𝑚_𝑖𝑗 = 𝐠^𝑙m 𝜞_𝑖𝑗𝑙,  ∴ 𝜞^𝑚_𝑖𝑗 = 𝐠^𝑙m 𝜞_𝑖𝑗𝑙   [14.3.2-6]
               𝜞^𝑘_𝑖𝑗 = 𝜞^𝑘_𝑗𝑖 =  𝐠^𝑘 ∙ 𝐠_𝑖.𝑗 =  𝐠^𝑘 ∙ 𝐠_𝑗.𝑖 = -𝐠_𝑖 ∙ 𝐠^𝑘_.𝑗  <- covariant vector의 미분 참조; 𝜞_𝑖𝑗𝑘 = 𝜞_𝑗𝑖𝑘 = 𝐠_𝑘 ∙ 𝐠_𝑖.𝑗 = 𝐠_𝑘 ∙ 𝐠_𝑗.𝑖   [14.3.7,8]
        ∘ 2종 Christoffel 기호의 계산  <- ※ 핵심적인 계산!
               𝑔_𝑖𝑗 = 𝐠_𝑖 ∙ 𝐠𝑗, 이를 좌표계에 대해서 미분하면,   ∂𝑔_𝑖𝑗/∂𝜉^𝑘 = 𝐠_𝑖.𝑘 ∙ 𝐠_𝑗 +  𝐠_𝑖 ∙ 𝐠_𝑗.𝑘   [14.3.9]
              ∴ ∂𝑔_𝑖𝑗/∂𝜉^𝑘 = 𝜞_𝑖𝑘𝑗 + 𝜞_𝑗𝑘𝑙 [a], ∂𝑔_𝑗𝑘/∂𝜉^𝑖 = 𝜞_𝑗𝑖𝑘 + 𝜞_𝑘𝑖𝑗 [b], ∂𝑔_𝑘𝑖/∂𝜉^𝑗 = 𝜞_𝑘𝑗𝑖 + 𝜞_𝑖𝑗𝑘 [c], [b]+[c]-[a] → 𝜞_𝑖𝑗𝑘= (1/2) (𝑔_{𝑗𝑘.𝑖}+ 𝑔_{𝑘𝑖.𝑗}- 𝑔_{𝑖𝑗.𝑘})   [14.3.10-14]
              ∵ 𝜞^𝑝_𝑖𝑗 = 𝑔^𝑘𝑝 𝜞_𝑖𝑗𝑘,  𝜞^𝑝_𝑖𝑗 = (1/2) 𝑔^𝑘𝑝 (𝑔_{𝑗𝑘.𝑖}+ 𝑔_{𝑘𝑖.𝑗}- 𝑔_{𝑖𝑗.𝑘})  <- 직접 사용이 복잡하므로 지수값에 따라 나누어 계산함   [14.3.15]
               * 실제의 계산 방식:  𝜞^𝑘_𝑖𝑗 = 0  [𝑖≠𝑗≠𝑘 일 때],  [이하 𝑖̄𝑖̄, 𝑘̄𝑘̄: 중복 지수 미적용]  𝜞^𝑘_𝑖𝑖 = (-1/2 𝑔_𝑘̄𝑘̄)(∂𝑔_𝑖̄𝑖̄/∂𝜉^𝑘)    [14.3.16,17]
                                              𝜞^𝑘_𝑘𝑗 = 𝜞^𝑘_𝑗𝑘 = (1/2𝑔_𝑘̄𝑘̄)(∂𝑔_𝑘̄𝑘̄/∂𝜉^𝑗) = (1/2){∂ ln(𝑔_𝑘̄𝑘̄/∂𝜉^𝑗},    𝜞^𝑘_𝑘̄𝑘̄ = (1/2𝑔_𝑘̄𝑘̄)(∂𝑔_𝑘̄𝑘̄/∂𝜉^𝑘)  [14.3.18,19]
           ex) 원통 좌표계에서의 2종 Christoffel 기호를 구하시오.  ◂
                 𝜞²₁₂ = 𝜞²₂₁ = (1/2)∂𝑔_𝑘̄𝑘̄/∂𝜉^𝑗) = (1/2)∂ ln(𝑔₂₂)/∂𝜉¹ = (1/2)∂ ln(𝑟²)/∂𝑟 = 1/𝑟,  𝜞¹₂₂ = -(1/2𝑔₁₁)∂𝑔₂₂/∂𝜉¹ = -(1/2)∂𝑟²)/∂𝑟 = -𝑟,  기타: 0  ▮
        ∘ Unit basis vector의 미분: 𝐞_𝑖 = 𝐠_𝑖/√ 𝑔_𝑖̄𝑖̄,  𝐞_𝑖.𝑗 = (1/√ 𝑔_𝑖̄𝑖̄) 𝐠_𝑖.𝑗 + 𝐠_𝑖(1/√ 𝑔_𝑖̄𝑖̄)_.𝑗  <- 양변을 𝜉^𝑗로 미분   [14.3.22,23]
                (1/√ 𝑔_𝑖̄𝑖̄) 𝐠_𝑖.𝑗= (1/√ 𝑔_𝑖̄𝑖̄) 𝜞^𝑘_𝑖𝑗) 𝐠_𝑘 = (1/√ 𝑔_𝑖̄𝑖̄) 𝜞^𝑘_𝑖𝑗 (√ 𝑔_𝑘̄𝑘̄) 𝐞_𝑘;  𝐠_𝑖(1/√ 𝑔_𝑖̄𝑖̄)_.𝑗 = -{1/2(𝑔_𝑖̄𝑖̄)^3/2}𝑔_{𝑖̄𝑖̄.𝑗} 𝐠_𝑖 = -{1/2(𝑔_𝑖̄𝑖̄)^3/2}𝑔_{𝑖̄𝑖̄.𝑗}√ 𝑔_𝑖̄𝑖̄ 𝐞_𝑖   [14.3.24,25]
                = -(1/2𝑔_𝑖̄𝑖̄) 𝑔_{𝑖̄𝑖̄.𝑗} 𝐞_𝑖;  ∴ 𝐞_𝑖.𝑗 = √ (𝑔_𝑘̄𝑘̄/𝑔_𝑖̄𝑖̄) 𝜞^𝑘_𝑖𝑗 𝐞_𝑘 - (1/2𝑔_𝑖̄𝑖̄) 𝑔_{𝑖̄𝑖̄.j} 𝐞_𝑖  <- 𝑖̄𝑖̄, 𝑘̄𝑘̄: dummy index 미적용 표기   [14.3.25,26]
           ex) 원통 좌표계 (𝜉¹ = 𝑟, 𝜉² = 𝜃, 𝜉³ = 𝑧)에서의 단위 기저 벡터의 미분값을 구하시오.  ◂
                 ∂𝐞₁/∂𝜉¹ = 𝐞₁ 𝜞¹₁₁ √ 𝑔₁₁/𝑔₁₁ + 𝐞₂ 𝜞²₁₁ √ 𝑔₂₂/𝑔₁₁ + 𝐞₃ 𝜞³₁₁ √ 𝑔₃₃/𝑔₁₁ - 𝐞₁(1/2𝑔₁₁)(∂𝑔₁₁/∂𝜉¹ = 0   [14.3.27]
                 ∂𝐞₁/∂𝜉² = 𝐞₁ 𝜞¹₁₁ √ 𝑔₁₁/𝑔₁₁ + 𝐞₂ 𝜞²₁₁ √ 𝑔₂₂/𝑔₁₁ + 𝐞₃ 𝜞³₁₁ √ 𝑔₃₃/𝑔₁₁ - 𝐞₁(1/2𝑔₁₁)(∂𝑔₁₁/∂𝜉² = 0   [14.3.28]
                 ∂𝐞₁/∂𝑟 = 0,  ∂𝐞₂/∂𝑟 = 0,  ∂𝐞₃/∂𝑟 = 0,  ∂𝐞₁/∂𝜃 = 𝐞₂,  ∂𝐞₂/∂𝜃 = -𝐞₂,  ∂𝐞₃/∂𝜃 = 0,  ∂𝐞₁/∂𝑧 = 0,  ∂𝐞₂/∂𝑧 = 0,  ∂𝐞₃/∂𝑧 = 0  ▮   [14.3.29]
      d) Tensor의 미분: 2차 tensor 𝐀 = 𝐴^𝑖𝑗 𝐠_𝑖 ⊗ 𝐠_𝑗,  𝐀 = 𝐴_𝑖𝑗 𝐠^𝑖 ⊗ 𝐠^𝑗,   𝐀 = 𝐴^𝑖_.𝑗 𝐠_𝑖 ⊗ 𝐠^𝑗 등의 좌표에 대한 미분
        ∘  ∂𝐀/∂𝜉^𝑘 = (∂𝐴^𝑖𝑗/∂𝜉^𝑘) 𝐠_𝑖 ⊗ 𝐠_𝑗 + 𝐴^𝑖𝑗 ∂𝐠_𝑖/∂𝜉^𝑘 ⊗ 𝐠_𝑗 + 𝐴^𝑖𝑗 𝐠_𝑖 ⊗ ∂𝐠_𝑗/∂𝜉^𝑘 = (∂𝐴^𝑖𝑗/∂𝜉^𝑘) 𝐠_𝑖 ⊗ 𝐠_𝑗 + 𝐴^𝑖𝑗 𝜞^𝑚_𝑖𝑘 𝐠_𝑚 ⊗ 𝐠_𝑗 + 𝐴^𝑖𝑗 𝜞^𝑚_𝑗𝑘 𝐠_𝑖 ⊗ 𝐠_𝑚   [14.4.1,2]
                     = (∂𝐴^𝑖𝑗/∂𝜉^𝑘) 𝐠_𝑖 ⊗ 𝐠_𝑗 + 𝐴^𝑚𝑗 𝜞^𝑖_𝑚𝑘 𝐠_𝑖 ⊗ 𝐠_𝑗 + 𝐴^𝑖𝑚 𝜞^𝑗_𝑚𝑘 𝐠_𝑖 ⊗ 𝐠_𝑗 = (∂𝐴^𝑖𝑗/∂𝜉^𝑘 + 𝐴^𝑚𝑗 𝜞^𝑖_𝑚𝑘 + 𝐴^𝑖𝑚 𝜞^𝑗_𝑚𝑘) 𝐠_𝑖 ⊗ 𝐠_𝑗 = 𝐴^𝑖𝑗∣_𝑘 𝐠_𝑖 ⊗ 𝐠_𝑗   [14.4.3]
              ∴ If 𝐀 = 𝐴^𝑖𝑗 𝐠_𝑖 ⊗ 𝐠_𝑗, then ∂𝐀/∂𝜉^𝑘 = 𝐴^𝑖𝑗∣_𝑘 𝐀 = (∂𝐴^𝑖𝑗/∂𝜉^𝑘 + 𝐴^𝑚𝑗 𝜞^𝑖_𝑚𝑘 + 𝐴^𝑖𝑚 𝜞^𝑗_𝑚𝑘) 𝐀 <- 자연 기저 vector에 대한 contravariant 미분   [14.4.4]
        ∘  ∂𝐀/∂𝜉^𝑘 = (∂𝐴_𝑖𝑗/∂𝜉^𝑘) 𝐠^𝑖 ⊗ 𝐠^𝑗 + 𝐴_𝑖𝑗 ∂𝐠^𝑖/∂𝜉^𝑘 ⊗ 𝐠^𝑗 + 𝐴_𝑖𝑗𝐠^𝑖 ⊗ ∂𝐠^𝑗/∂𝜉^𝑘 =  (∂𝐴_𝑖𝑗/∂𝜉^𝑘 - 𝐴_𝑚𝑗 𝜞^𝑚_𝑘𝑖 - 𝐴_𝑖𝑚 𝜞^𝑚_𝑘𝑗) 𝐠^𝑖 ⊗ 𝐠^𝑗 = 𝐴_𝑖𝑗 ∣_𝑘 𝐠^𝑖 ⊗ 𝐠^𝑗   [14.4.5,6]
              ∴ If 𝐀 = 𝐴_𝑖𝑗 𝐠^𝑖 ⊗ 𝐠^𝑗, then  ∂𝐀/∂𝜉^𝑘 = 𝐴_𝑖𝑗∣_𝑘 𝐀 = (∂𝐴_𝑖𝑗/∂𝜉^𝑘 - 𝐴_𝑚𝑗 𝜞^𝑚_𝑘𝑖 - 𝐴_𝑖𝑚 𝜞^𝑚_𝑘𝑗) 𝐀 <- 역기저 vector에 대한 covariant 미분   [14.4.7]
        ∘   .... If 𝐀 = 𝐴^𝑖_.𝑗 𝐠_𝑖 ⊗ 𝐠^𝑗, then ∂𝐀/∂𝜉^𝑘 = 𝐴^𝑖_.𝑗∣_𝑘 𝐀 = (∂𝐴^𝑖_.𝑗/∂𝜉^𝑘 + 𝐴^𝑚_.𝑗 𝜞^𝑖_𝑘𝑚 - 𝐴^𝑖_.𝑚 𝜞^.𝑚_𝑗𝑘) 𝐀 <- 혼합 성분에 대한 미분   [14.4.8]
      e) Gradient(구배) : 𝛁𝜙  or  𝛁𝐮  or  𝛁𝐀  <- 𝛁 ≡ 𝐠^𝑗 ∂/∂𝜉^𝑗 사용 (이하 동일)
        ∘ scala field 구배: 𝛁𝜙 ≡ 𝐠^𝑗 ∂𝜙/∂𝜉^𝑗;  𝛁𝜙  = 𝜙_.𝑗 𝐠^𝑗 or 𝜙_.𝑗;  𝛁𝜙 =  𝜙_.𝑗 𝐠^𝑗 = 𝑔^𝑖𝑗𝜙_.𝑗 𝐠_𝑖 = 𝑔^𝑖𝑗√ 𝑔_𝑖̄𝑖̄ 𝜙_.𝑗 𝐞_𝑖   [14.5.1-3]
        ∘ vector field 구배: 𝐮 = 𝑢_𝑖 𝐠^𝑖 = 𝑢^𝑖 𝐠_𝑖 경우
           𝛁𝐮 = 𝛁 ⊗ 𝐮 = 𝐠^𝑗 ∂𝐮/∂𝜉^𝑗 = 𝑢_𝑖∣_𝑗 𝐠^𝑖 ⊗ 𝐠^𝑗 =  𝑢^𝑖∣_𝑗 𝐠_𝑖 ⊗ 𝐠^𝑗  <- 𝑢_𝑖∣_𝑗 = 𝑢_𝑖,𝑗 - 𝑢_𝑘 𝜞^𝑘_𝑖𝑗,  𝑢^𝑖∣_𝑗 = 𝑢^𝑖_,𝑗 + 𝑢^𝑘 𝜞^𝑖_𝑘𝑗  or  𝑢_𝑖∣_𝑗 = 𝑔^𝑖𝑘𝑢^𝑘∣_𝑗   [14.5.5,6]
        ∘ tensor field 구배: 𝐀 = 𝐴_𝑖𝑗 𝐠^𝑖 ⊗ 𝐠^𝑗 = 𝐴^𝑖_.𝑗 𝐠_𝑖 ⊗ 𝐠^𝑗 경우 (다른 경우도 유사한 방법 적용)
            𝛁𝐀 =  𝐠^𝑘 ∂𝐀/∂𝜉^𝑗 =  𝐴_𝑖𝑗∣_𝑘 𝐠^𝑖 ⊗ 𝐠^𝑗 ⊗ 𝐠^𝑘 = 𝐴^𝑖_.𝑗∣_𝑘 𝐠_𝑖 ⊗ 𝐠^𝑗 ⊗ 𝐠^𝑘   [14.5.7]
      f) Divergence(발산): 𝛁 ∙ 𝐮  or  𝛁 ∙ 𝐀
        ∘ vector field 발산: 𝐮 = 𝑢^𝑖 𝐠_𝑖 경우
              𝛁 ∙ 𝐮 = 𝐠^𝑗 ∂/∂𝜉^𝑗 ∙ 𝐮 =  𝐠^𝑗 ∙ (𝑢^𝑖 𝐠_𝑖)_.𝑗 = 𝐠^𝑗 ∙ 𝑢^𝑖∣_𝑗 𝐠_𝑖 = 𝑢^𝑖∣_𝑗 𝐠^𝑗 ∙ 𝐠_𝑖 = 𝑢^𝑖∣_𝑗 𝛿^𝑗_𝑖 = 𝑢^𝑖∣_𝑖   [14.6.1]
             ∴ 𝛁 ∙ 𝐮 = 𝑢^𝑖∣_𝑖 = ∂𝑢^𝑖/∂𝜉^𝑖 + 𝑢^𝑘𝜞^𝑖_𝑘𝑖 = (1/√𝑔) ∂ √𝑔 𝑢^𝑖/∂𝜉^𝑖   [14.6.2]  <- ※ ** why? 유도 과정이 없이 나타남
              𝛁 ∙ 𝐮 = 𝑢^𝑖∣_𝑖 = (1/√𝑔){∂(√𝑔 𝑢^(𝑖)/√𝑔_𝑖𝑖)/∂𝜉^𝑖}  (𝑢^𝑖 = 𝑢^(𝑖)/√𝑔_𝑖𝑖)  or  𝛁 ∙ 𝐮 = tr(𝛁𝐮) = 𝛁𝐮 : 𝐈   [14.6.3,4]
             ex) 원통 좌표계 (𝜉¹ = 𝑟, 𝜉² = 𝜃,  𝜉³ = 𝑧)에서 vector 장 𝐮 = 𝑢^𝑖 𝐠_𝑖의 발산을 구하고 물리적 성분으로 표시하시오. ◂
                   𝛁 ∙ 𝐮 = (1/√𝑔)(∂/∂𝜉^𝑖)(√ 𝑔 𝑢^𝑖) = (1/√ 𝑔){(∂/∂𝜉¹)(√ 𝑔 𝑢¹) + (∂/∂𝜉²)(√ 𝑔 𝑢²) + (∂/∂𝜉³)(√ 𝑔 𝑢³)}
                          = 1/𝑟{(∂/∂𝑟)𝑟𝑢_𝑟 + (∂/∂𝜃)𝑢_𝜃 + (∂/∂𝑧)𝑟𝑢_𝑧} = ∂𝑢_𝑟/∂𝑟 + (1/𝑟)(∂𝑢_𝜃/∂𝜃 + 𝑢_𝑟) + ∂𝑢_𝑧/∂𝑧   [14.6.5]
                   𝑔₁₁ = 𝑔₃₃ = 1,  𝑔₂₂ = 𝑟² 기타: 0,  𝑔 (≡ det [𝑔_𝑖𝑗]) = 𝑟²,  𝐞_𝑖 = 𝐠_𝑖/∥𝐠∥ = 𝐠_𝑖/√ 𝑔_𝑖̄𝑖̄;  물리적 성분 𝑢¹ = 𝑢^𝑟,  𝑢² = 𝑢_𝜃/𝑟,  𝑢³ = 𝑢^𝑧 ▮
        ∘ tensor field 발산: 𝐀 = 𝐴^𝑖𝑗 𝐠_𝑖 ⊗ 𝐠_𝑗 경우
                  𝛁 ∙ 𝐀 = 𝐠^𝑘 ∙ ∂𝐀/∂𝜉^𝑘 = 𝐠^𝑘 ∙ 𝐴^𝑖𝑗∣_𝑘 𝐠_𝑖 ⊗ 𝐠_𝑗 = 𝐴^𝑖𝑗∣_𝑘 (𝐠^𝑘 ∙ 𝐠_𝑖) 𝐠_𝑗 = 𝐴^𝑖𝑗∣_𝑘 𝛿^𝑘_𝑖 𝐠_𝑗 = 𝐴^𝑖𝑗∣_𝑖 𝐠_𝑗  <- tensor의 미분,  𝐚 ∙ (𝐛 ⊗ 𝐜) = (𝐚 ∙ 𝐛) 𝐜   [14.6.7-9]
      g) Laplacian: 𝛁²𝜙  or  𝛁²𝐯
              𝛁² = 𝛁 ∙ 𝛁 = 𝐠^𝑖 ∂/∂𝜉^𝑖 ∙ (𝐠^𝑗 ∂/∂𝜉^𝑖) = 𝐠^𝑖 (∂𝐠^𝑗/∂𝜉^𝑖)(∂/∂𝜉^𝑖) + 𝐠^𝑖 ∙ 𝐠^𝑗 ∂²/(∂𝜉^𝑖∂𝜉^𝑗)  <- by product rule
                                 = 𝑔^𝑖𝑘 𝐠_𝑘 ∙ (∂𝐠^𝑗/∂𝜉^𝑖)(∂/∂𝜉^𝑖) + 𝑔^𝑖𝑗(∂²/∂𝜉^𝑖∂𝜉^𝑗) = 𝑔^𝑖𝑗(∂²/∂𝜉^𝑖∂𝜉^𝑗) - 𝑔^𝑖𝑘𝜞^𝑗_𝑖𝑘(∂/∂𝜉^𝑖) <- metric tensor, kronecker delta   [14.7.1]
             ∴ 𝛁² = 𝑔^𝑖𝑗(∂²/∂𝜉^𝑖∂𝜉^𝑗) - 𝑔^𝑖𝑘𝜞^𝑗_𝑖𝑘(∂/∂𝜉^𝑖)   [14.7.2]
        ∘ scala field Laplacian: 𝛁²𝜙 = 𝛁 ∙ 𝐯 = (1/√𝑔) ∂√𝑔 𝑣^𝑖/∂𝜉^𝑖 = (1/√𝑔) ∂√𝑔 𝑔^𝑗𝑖𝜙_.𝑖/∂𝜉^𝑖  <- vector field 발산, scalar의 구배, 𝑣^𝑖 =  𝑔^𝑗𝑖𝜙_.𝑖   [14.7.3]
        ∘ vector field Laplacian: 𝛁²𝐯 = 𝑔^𝑖𝑗∂²𝐯/∂𝜉^𝑖∂𝜉^𝑗 - 𝑔^𝑖𝑘𝜞^𝑗_𝑖𝑘∂𝐯/∂𝜉^𝑖   [14.7.6]

p.s.  * why? [14.2.19]: vector (𝐚 ∙ 𝐛) 𝐜 = 𝐚 (𝐛 ∙ 𝐜) 관계식이 성립하는지는 나중에 ...

Name

Spamfree

여기를 클릭해 주세요.

Password

Comment

답글쓰기

목록보기

번호	제 목	이름	연관	날짜	조회
121	Waves 5. Electromagnetic wave equation	김관석	8	2024-05-07 09:24:42	1306
120	Waves 6. Quantum wave equation	김관석	8	2024-05-07 09:24:42	1306
119	Gravirational Collapse and Space-Time Singularities 📚 🔵	김관석	1	2023-06-12 13:50:03	5482
118	Mathematics of Astronomy 1. Gravity; Light ✅	김관석	4	2023-05-02 08:31:40	1542
117	Mathematics of Astronomy 2. Parallax, angular size etc.	김관석	4	2023-05-02 08:31:40	1542
116	Mathematics of Astronomy 3. Stars	김관석	4	2023-05-02 08:31:40	1542
115	Mathematics of Astronomy 4. Black holes & cosmology	김관석	4	2023-05-02 08:31:40	1542
114	Still의 <블록으로 설명하는 입자물리학> ✅	김관석	3	2022-04-14 18:49:01	1048
113	Becker의 <실재란 무엇인가?>	김관석	3	2022-04-14 18:49:01	1048
112	Penrose의 <시간의 순환> (강추!) [u. 5/2023] 🌹	김관석	3	2022-04-14 18:49:01	1048
111	일반상대성(GR) 학습에 대하여..	김관석	1	2022-01-03 09:49:28	370
110	HTML(+) 리뷰/홈페이지 운용^^ [1]	김관석	1	2021-11-08 16:52:09	249
109	Peebles의 Cosmology's Century (2020)	김관석	1	2021-08-16 21:08:03	439
108	<한권으로 충분한 우주론> 외 ✅	김관석	5	2021-06-06 13:38:14	2248
107	Rovelli의 <보이는 세상은 실재가 아니다>	김관석	5	2021-06-06 13:38:14	2248
106	Smolin의 <양자 중력의 세가지 길>	김관석	5	2021-06-06 13:38:14	2248
105	Susskind의 <우주의 풍경> (강추!) 🌹	김관석	5	2021-06-06 13:38:14	2248
104	대중적 우주론 추천서 목록 [u. 9/2021] [1]	김관석	5	2021-06-06 13:38:14	2248
103	Zel'dovich's Relativistic Astrophysics ✅	김관석	1	2021-04-01 08:16:42	1333
102	Dirac Equation and Antimatter	김관석	1	2021-03-15 12:49:45	597
101	11/30 태양 흑점 sunspots ✅	김관석	2	2020-11-30 16:14:27	1011
100	Coronado PST 태양 사진^^	김관석	2	2020-11-30 16:14:27	1011
99	Linde's Inflationary Cosmology [u. 1/2021]	김관석	1	2020-11-06 09:19:06	907
98	The Schrödinger Equation (7) Harmonic Oscillator ✅	김관석	1	2020-09-17 21:43:31	2720
97	현대 우주론의 명저 Weinberg의 <최초의 3분> ✅	김관석	3	2020-08-09 11:37:44	1430
96	물리학도를 위한 현대 우주론서는?	김관석	3	2020-08-09 11:37:44	1430
95	현대 우주론의 최고, 최신, 고전서.. [u. 10/2024] [1]	김관석	3	2020-08-09 11:37:44	1430
94	Mathematical Cosmology 1. Overview 🔵	김관석	6	2020-06-07 16:23:00	5715
93	Mathematical Cosmology 2. FRW geometry	김관석	6	2020-06-07 16:23:00	5715
92	Mathematical Cosmology 3. Cosmological models I	김관석	6	2020-06-07 16:23:00	5715
91	Mathematical Cosmology 4. Cosmological models II	김관석	6	2020-06-07 16:23:00	5715
90	Mathematical Cosmology 5. Inflationary cosmology	김관석	6	2020-06-07 16:23:00	5715
89	Mathematical Cosmology 6. Perturbations	김관석	6	2020-06-07 16:23:00	5715
88	Hobson Efstathiou Lasenby GR 11a. Schwartzschild 블랙홀 🔴 [2]	김관석	3	2020-05-13 13:44:21	17694
87	Hobson et al. GR 11b. 중력의 붕괴, 블랙홀 형성	김관석	3	2020-05-13 13:44:21	17694
86	Hobson et al. GR 11c. 웜홀, Hawking 효과	김관석	3	2020-05-13 13:44:21	17694

목록보기 이전페이지 다음페이지 글쓰기

[1] 2 [3][4][5]