|
김관석
|
2019-06-16 16:50:51, 조회수 : 1,118 |
- Download #1 : dff_1_1.jpg (47.4 KB), Download : 5

중력(gravity)은 시공간의 curvature * 휘어짐의 발현이라는 아인슈타인의 상대성이론의 이해를 위해서 공간과 시간을
기하학적 이론으로서 파악하는 것이 이 책의 궁극적인 목표입니다. 그 중에서는 바로 curvature가 주축이 되는 개념입니다.
curvature의 개념은 4차원 이상에서는 더욱 복잡해지므로, Euclid 3차원 공간 E3에서의 curvature를 먼저 논의합니다.
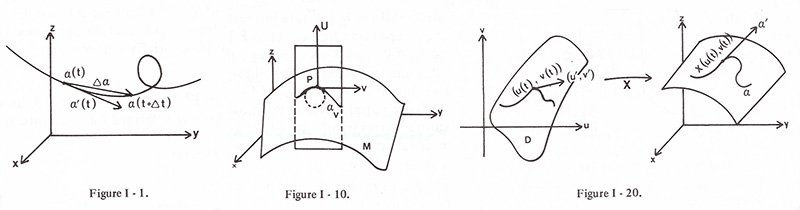
1. Curves 曲線 <- Figure I-1 참조
∘ 𝛂(t) = (x(t),y(t),z(t)) <- 𝛂: vector-valued fuction curve in 𝐄3, a ≤ t ≤ b, t: real variable parameter 媒介變數
∘ 𝛂'(t) = (x'(t),y'(t),z'(t)) = lim𝛥→0 [𝛂(t + 𝛥t) - 𝛂(t))]/𝛥t <- 𝛂': derivative vector of curve 𝛂
∘ s(t) = ∫at∥𝛂'(u)∥du <- s: arc length of curve 𝛂, t: time, ∥𝛂'(u)∥: instaneous speed 速力, 𝛂': velocity vector
∘ 𝐋 = ∫ab∥𝛂'(u)∥du <- 𝐋: total length of the entire curve 𝛂(t), a ≤ t ≤ b, 𝐈: interval
∘ 𝛂"(t) = (x"(t),y"(t),z"(t)) <- 𝛂": derivative of velocity vector 𝛂', 𝛂": acceleration vector
∘ 𝐓(s) = 𝛂'(s) <- t = s → ds/dt = 1, 𝛂'(s) or 𝐓(s): unit tangent vector, 𝛂(s): unit speed curve
∘ 𝐓(s) ∙ 𝐓(s) = 1, ∴ 𝐓(s) ∙ 𝐓'(s) = 0 (<- by product rule) ∴ 𝐓(s)⊥𝐓'(s), 𝛂"(s) or 𝐓'(s): curvature vector
∘ Definition I-1
k(s) = ∥𝐓'(s)∥= ∥𝛂"(s)∥
k(s)로 지칭되는 곡선 𝛂의 𝛂(s)에서의 curvature 曲率은 𝐓'(s)의 길이이다.
∘ 𝐍(s) = 𝐓'(s)/∥𝐓'(s)∥= 𝐓'(s)/k(s). ∴ 𝐓'(s) = k(s)𝐍(s) <- 𝐍(s): principal normal vector
∘ c(s) = 𝛂(s) + [1/k(s)]/𝐍(s) <- 𝛂(s): 곡선 𝛂에의 tangent point, c(s): center of curvature
osculating circle 接觸圓: 반지름 1/k(s), 중심 c(s)의 원, osculating plane: 𝐓(s)와 𝐍(s)의 평면
∘ 𝐁 = 𝐓 X 𝐍 <- binormal vector of the unit length: osculating plane에 수직인 vector
𝐁' = (𝐓 X 𝐍)' = 𝐓' X 𝐍 + 𝐓 X 𝐍' = 0 + 𝐓 X 𝐍'= 𝐓 X 𝐍' (∵ 𝐓'= k𝐍)
𝐍 = 𝐁 X 𝐓, 𝐓 = 𝐍 X 𝐁, 𝐍⊥𝐁, 𝐍⊥𝐍', 𝐁'⊥𝐁, 𝐁'⊥𝐍' ∴ 𝐁' ∝𝐍
∘ 𝐁' = - 𝜏𝐍 <- 𝜏 = 𝜏(s): torsion 비틀림(꼬임) 함수로서 osculating plane의 turning rate(回轉 比率)를 측정함.
∘ 𝐓' = k𝐍, 𝐍' = - k𝐓 + 𝜏𝐁, 𝐁' = - 𝜏𝐍 <- the Formulas of Frenet
아주 간략하게 요약한 이상의 관계식을 제대로 이해한다면 우리는 3차원에서의 임의의 곡선을 해석/재현할 수 있습니다.
2. Gauss Curvature I <- Figure I-10 참조
∘ 매끄러운(smooth) 곡면(surface) 𝐌 ⊂ 𝐄3에 임의의 점 𝐏에 unit normal vector를 𝐔라고 합니다. 이때 𝐯가 점 𝐏에서
𝐌에 접하는 unit vector라면, 그 𝐯에 의존하는 𝛂𝐯 곡선이 있는 𝐌과 𝐏에서 교차하는 평면은 𝐯와 𝐔에 의해 결정됩니다.
그래서 우리는 𝛂𝐯를 곡면 𝐌의 점 𝐏에서의 normal section in the 𝐯 direction 이라고 부릅니다.
∘ 𝐤n(𝐯) = ∓1/ 𝐑(𝐯) <- 𝐑(𝐯): osculating circle 반경, 𝐤n(𝐯): 𝐌의 𝐏에서 normal curvature in the 𝐯 direction
𝛂𝐯의 principal normal vector와 surface normal vector인 𝐔의 방향이 동일하면 +, 반대이면 -, curvature가 0이면 0.
∘ Gauss curvature 𝐊 (𝐌의 𝐏에서)란?
𝐊(𝐏) = 𝐤1 𝐤2 <- 𝐯1: tangent vector in a principal direction 𝐤1: maxinmum value of 𝐤n(𝐯),
𝐯2: tangent vector in a principal direction 𝐤2: minimum value of 𝐤n(𝐯), 𝐯1 and 𝐯1: 항상 직교함.
ex1) 𝐊 in a cylinder: (반경 R인 경우) 𝐤1= 1/R, 𝐤2= 0 ∴ 𝐊 = 0
ex2) 𝐊 in a sphere: (반경 R인 경우) 𝐤n(𝐯) = ∓1/R2
ex3) 𝐊 in a sddle-shaped surface: z = 1/2(y2 - x2), 𝐊 < 0
ex4) 𝐊 in a torus: 𝐊 > 0 on outside surface, 𝐊 > 0 on inside surface, 𝐊 = 0 on two circle of top and bottom
Curvature의 intrinsic 內在的 표기 덕분에 일반상대성원리의 4차원 시공간 curvature를 정의할 수 있습니다.
Gauss의 Therema Egregium (빼어난 定理)로 절정을 이루는 곡면 이론 덕분에 intrinsic 표기가 가능해졌습니다.
intrinsic한 curvature의 재공식화는 고차원의 manifold 多樣體와 'curved space'를 일반화할 수 있게 합니다.
3. Surfaces 曲面 in E3 <- Figure I-20 참조
∘ 곡면 𝐌은 𝓡2의 open subset 𝐃에 정의된 두개 변수의 vector 함수 𝐗:𝐃 → E3의 image로 locally(局所的으로) 표기 가능
𝐗 = 𝐗(u,v) = (x(u,v), y(u,v), z(u,v)) [3-2]
∘ 편의상 우리는 이 함수를 𝐃에서 최소 삼차까지 미분할 수 있으며, 𝐗가 regular 正則的일 때는 다음의 경우
𝐗1(u, v) = ∂𝐗/∂u = (∂x/∂u, ∂y/∂u, ∂z/∂u)
𝐗2(u, v) = ∂𝐗/∂v = (∂x/∂v, ∂y/∂v, ∂z/∂v)
상기 두 vector는 𝐃의 각 (u,v)에 대해 linearlly independnt(線形 獨立)하여서, 𝐗1 X 𝐗2 ≠ 0 in 𝐃.
∘ 일반적으로 regularity(正則性)은 𝐃의 각 점들이 neighborhood(近傍) 𝛺를 갖으며, 이에 대해 함수 𝐗가
연속적인 inverse function(逆函數) 𝐗(𝛺) → 𝛺 를 갖는 one-to-one(一對一)의 관계를 보장합니다. 그래서
이러한 대응을 system of curvillinear coordinate(曲線 座標系) u, v on 𝐗(𝛺) ⊂ 𝐌으로 생각할 수 있습니다.
∘ 𝛂(t) = 𝐗 (u(t), v(t)) <- 𝐃에서 u(t), v(t)가 smooth 곡선이면, 𝐗에 의한 image도 𝐌에서 𝛂도 smooth 곡선
𝛂'(t) = (∂𝐗/∂u)(du/dt) + (∂𝐗/∂v)(dv/dt) <- by chain rule
𝛂'(t) = u'𝐗1 + v'𝐗2 <- in abbriviated notation [3-3]
∘ Definition I-2
𝐌에서 𝐏를 통과하는 곡선의 velociy vector 𝐯가 𝐏에 있으면, vector 𝐯를 𝐏에서 𝐌으로의 tangent vector 라 부른다.
𝐏에서 𝐌으로의 모든 tangent vector의 집합은 𝐏에서 𝐌의 tangent plane 라고 부르고, 𝐓p𝐌으로 표기한다.
∘ 𝐏에서의 어떤 tangent vector 𝐗(u0, v0)는 𝐗1(u0, v0)과 𝐗1(u0, vo)의 한 linear combination입니다.
거꾸로 실수 a, b와의 linear combination 𝐯 = (a𝐗1 + b𝐗2)(u0, v0)는 𝐌에 있는 한 곡선의 velocity vector입니다.
예를 들면 𝛂(t) = 𝐗(u0+ at, v0+ bt)는 𝛂'(0) = 𝐯 를 갖습니다. 그래서 regurality(正則性) of 𝐗란 𝐓p𝐌가
𝐗1과 𝐗2를 basis(기저)로 하는 각 점 𝐏에서의 2-dimensional vector space를 의미하는 것입니다.
이때 𝐗1(u0, v0)과 𝐗2(u0, v0)는 그들 자신이 그 곡선의 velocity vectors
u→ 𝐗 (u, v0) (v = v0, fixed) <- u-parameter curve
v→ 𝐗 (u0, v) (u = u0, fixed) <- v-parameter curve
p.s. Richard L. Faber Differential Geometry and Relativity Theory (Marcel Deckker 1983) Chapter I.
미분기하학과 상대성 원리에 관심을 둔 영어권 대학교 수학과/물리학과 고학년생들을 대상으로 집필되었다 함.
여러 GR책들을 살펴 보다가 수학적 rigor와 바탕이 필요한 제게 아주 적합한 책으로 생각되어 선정하였음.
* curvature는 문맥에 따라 휘어짐 자체를 의미하거나 곡률을 지칭 |
|
|





































