|
김관석
|
2019-06-16 16:55:58, 조회수 : 2,157 |
- Download #1 : dff_1_4.jpg (54.1 KB), Download : 6

8. Curvature Tensor And The Theorema Egregium(빼어난 定理)
∘ The Gauss Formulars: 𝐗𝑖k = 𝛤h𝑖k 𝐗h + 𝐿𝑖k 𝐔, 𝑖k = 1,2 <- Eq.(17) [8-47]
∘ The Weingarten Formulars: 𝐔𝑗 = - 𝐿𝑗𝑖 𝐗𝑗, 𝑖 = 1,2; 𝐿𝑗𝑖 = 𝐿𝑖𝑘𝑔𝑘𝑗, 𝑖 = 1,2 <- Eq. (28) [8-48]
∘ Theorem I-11 (Theorema Egregium ) 빼어난 定理
한 곡면의 the Gauss cuvature는 the metric form, 그리고 그 첫번째와 두번째 derivatives(導函數)의 계수들의 함수이다.
그러므로 intrinsic하다(內在的이다).
Proof. 𝐗𝑖k𝑗 = ∂𝛤h𝑖k/∂u𝑗 𝐗h + 𝛤h𝑖k 𝐗h𝑗 + ∂𝐿𝑖k/∂u𝑗 𝐔 + 𝐿𝑖k 𝐔𝑗 <- Eq. (47)의 양변을 u𝑗에 대해 미분하고 ∂𝐗𝑖k/∂u𝑗를 𝐗𝑖k 𝑗라 표기함
𝐗𝑖k𝑗 = (∂𝛤h𝑖k/∂u𝑗 + 𝛤r𝑖k𝛤hr𝑗 - 𝐿𝑖k𝐿h𝑗)𝐗h + (𝛤r𝑖k𝐿r𝑗 + ∂𝐿𝑖k/∂u𝑗) 𝐔 <- 𝐔𝑗 = - 𝐿h𝑗 𝐗h, 𝛤h𝑖k 𝐗h𝑗→ 𝛤r𝑖k 𝐗r𝑗(index 조정) [8-49]
𝐗𝑖𝑗k = (∂𝛤h𝑖𝑗/∂uk + 𝛤r𝑖𝑗𝛤hrk - 𝐿𝑖𝑗𝐿hk)𝐗h + (𝛤r𝑖𝑗𝐿rk + ∂𝐿𝑖𝑗/∂uk) 𝐔 <- switching 𝑗 and k [8-50]
∂𝛤h𝑖k/∂u𝑗 - ∂𝛤h𝑖𝑗/∂uk + 𝛤r𝑖k𝛤hr𝑗 - 𝛤r𝑖𝑗𝛤hrk = 𝐿𝑖k𝐿h𝑗 - 𝐿𝑖𝑗𝐿hk <- 𝐗𝑖k𝑗 = 𝐗𝑖𝑗k ∵ 偏微分의 순서는 무관함 [8-51]
𝑅h𝑖𝑗k = ∂𝛤h𝑖k/∂u𝑗 - ∂𝛤h𝑖𝑗/∂uk + 𝛤r𝑖k𝛤hr𝑗 - 𝛤r𝑖𝑗𝛤hrk, h,𝑖,𝑗,k = 1,2 <- Christoffel 기호는 𝑔𝑖𝑗관련 함수이므로 intrinsic! [8-52]
𝑅h𝑖𝑗k = -𝑅h𝑖k𝑗 <- Riemann-Christoffel curvature tensor * [8-53]
𝑅h𝑖𝑗k = 𝐿𝑖k𝐿h𝑗 - 𝐿𝑖𝑗𝐿hk <- Riemann-Christoffel curvature tensor on the second fundamental form [8-54]
𝑅m𝑖𝑗k ≡ 𝑔mh 𝑅h𝑖𝑗k <- by Eq. (52) intrinsic!; 𝑅r𝑖𝑗k ≡ 𝑔mr 𝑅mm𝑖𝑗k [inverse relation by Eq. (12)] [8-55]
𝑅m𝑖𝑗k = 𝐿𝑖k𝐿𝑗m - 𝐿𝑖𝑗𝐿km <- Eq. (54) 양변에 𝑔mh 곱하고 Eq. (27) [𝐿𝑖𝑗 ≡ 𝐿𝑗𝑘 𝑔𝑘𝑖, 𝑖,𝑗 =1,2]에 따라 정리함 [8-56]
𝐊 = 𝑅1212/𝑔 <- 𝑅1212 = 𝐿22𝐿11 - (𝐿21)2 = det (𝐿𝑖𝑗) = 𝐿; ∴ The Gauss cuvature is determined by the metric form. ▮ [8-57]
∘ The Formula for 𝐊 on the first fundamental form
𝑅m𝑖𝑗k = 𝑔mh ∂𝛤h𝑖k/∂u𝑗 + 𝛤r𝑖k 𝛤r𝑗m - switch(𝑗,k) <- by Eqs. (52). (55) and (33); ∵ 𝛤r𝑗m = 𝛤hr𝑗 𝑔mh
𝛤𝑖𝑗m = 𝑔mh 𝛤h𝑖k 양변을 u𝑗에 대해 미분 → ∂𝛤𝑖km/∂u𝑗 = 𝑔mh ∂𝛤h𝑖k/∂u𝑗 + 𝛤h𝑖k ∂𝑔mh/∂u𝑗, 𝑔mh ∂𝛤h𝑖k/∂u𝑗 = ∂𝛤𝑖km/∂u𝑗 - 𝛤h𝑖k ∂𝑔mh/∂u𝑗
∴ 𝑅m𝑖𝑗k = ∂𝛤𝑖km/∂u𝑗 + 𝛤h𝑖k 𝛤h𝑗m - 𝛤h𝑖k ∂𝑔hm/∂u𝑗 - switch(𝑗,k)
𝛤𝑖km = 1/2 (∂𝑔𝑖m/∂uk + ∂𝑔mk/∂u𝑖 - ∂𝑔k𝑖/∂um) <- by Eq. (36); ∂𝑔hm/∂u𝑗 = 𝛤h𝑗m + 𝛤m𝑗h = 𝛤h𝑗m + 𝛤rm𝑗 𝑔rh <- Eq. (35a)
𝑅m𝑖𝑗k = 1/2 (∂2𝑔𝑖m/∂u𝑗∂uk + ∂2𝑔mk/∂u𝑗∂u𝑖 - ∂2𝑔k𝑖/∂u𝑗∂um) + 𝛤h𝑖k 𝛤h𝑗m - 𝛤h𝑖k(𝛤h𝑗m + 𝛤rm𝑗 𝑔rh) - switch(𝑗,k)
𝑅m𝑖𝑗k = 1/2 (∂2𝑔km/∂u𝑗∂u𝑖 - ∂2𝑔𝑗m/∂u𝑖∂uk + ∂2𝑔𝑖𝑗/∂uk∂um - ∂2𝑔𝑖k/∂u𝑗∂um) + (𝛤h𝑖𝑗 𝛤rmk - 𝛤h𝑖k 𝛤rm𝑗)𝑔rh [8-58]
∴ 𝑅1212 = 1/2((∂2𝑔21/∂u1∂u2 - ∂2𝑔11/∂u2∂u2 + ∂2𝑔21/∂u2∂u1 - ∂2𝑔22/∂u1∂u1) + (𝛤h21 𝛤r12 - 𝛤h22 𝛤r11)𝑔rh
𝐊 = 𝑅1212/𝑔 = 1/𝑔[𝐹uv - 1/2 𝐸vv - 1/2 𝐺uu + (𝛤h21 𝛤r12 - 𝛤h22 𝛤r11)𝑔rh] → 直交座標系로 가정하면 𝐹 = 0; by Eq. 40 →
𝐊 = 1/𝐸𝐺 [- 1/2 𝐸vv - 1/2 𝐺uu + (𝐸v2/4𝐸2 + 𝐸u𝐺u/4𝐸2)𝐸 + (𝐺u2/4𝐺2 + 𝐸v𝐺v/4𝐺2)𝐺] → with a litte manipulation →
𝐊 = 1/(2√𝐸𝐺) [{√𝐸𝐺 𝐺uu- 𝐺u(𝐸𝐺u + 𝐸u𝐺)/(2√𝐸𝐺)}/𝐸𝐺 + {√𝐸𝐺 𝐸vv- 𝐸v(𝐸𝐺v + 𝐸v𝐺)/(2√𝐸𝐺)}/𝐸𝐺] or
𝐊 = 1/(2√𝐸𝐺) [∂(𝐺u/√𝐸𝐺)/∂u + ∂(𝐸v/√𝐸𝐺)/∂v] [8-59]
∘ The equation of 𝐊
Eq. (56) [𝑅m𝑖𝑗k = 𝐿𝑖k𝐿𝑗m - 𝐿𝑖𝑗𝐿km] looks like 24 = 16 equations but in fact only one equation 𝑅1212 = 𝐿 = 𝐊/𝑔! By Eq. (58),
𝑅m𝑖𝑗k = - 𝑅𝑖m𝑗k, 𝑅m𝑖𝑗k = - 𝑅𝑖mk𝑗, 𝑅m𝑖𝑗k = 𝑅𝑗km𝑖 <- antisymmetry: the first & last pair, symmetry: interchange of them [8-60abc]
𝑅11𝑗k = 𝑅22𝑗k = 𝑅m𝑖11 = 𝑅m𝑖22 = 0.
𝑅1212 = 𝑅2121 = - 𝑅2112 = - 𝑅1221 = 𝐊𝑔.
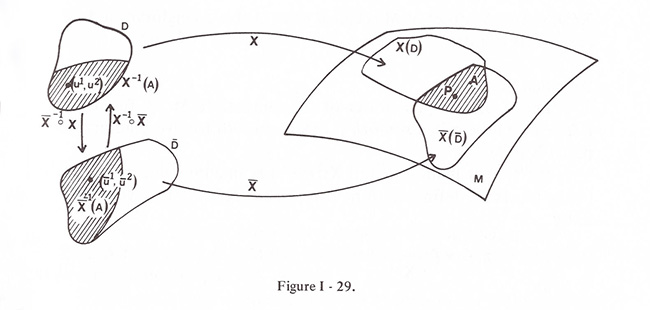
9. Manifolds(多樣體) <- Figure I-29 참조 [단, 𝐗→𝐗¹, 𝐃→𝐃¹; 𝐗̄→𝐗², 𝐃̄→𝐃²]
∘ E3 내의 surface 曲面의 일반화 필요성
첫째, 𝐗:𝐃 → E3라는 정의는 너무 제한적이라 단일 mapping이 안되기도 하며, 그 결과가 국지적 직관에 반할 수 있습니다.
둘째, 그 전개를 주어진 매개화한 𝐗로 하지만, 우리는 그 𝐗와 독립적으로 surface의 참된 기하학적 특성을 알기를 원합니다.
마지막으로, 우리는 이론의 내재적 부분을 고차원으로 확장해야 하는데, E3 vector에 대한 심한 의존이 심각한 결함입니다.
∘ 𝐌은 그 원소들을 points 点이라 부르는 non-empty set(非空 집합)으로 정의합니다. 또한 𝐌 상의 한 coordinate patch
座標 조각이란 E2의 열린 부분집합 𝐃에서 𝐌으로의 한 one-to-one function 𝐗:𝐃 → 𝐌입니다.
∘ Definition I-12
한 abstract surface or 2-manifold 는 다음 조건의 𝐌 상의 coordinate patch들의 collection 𝒞와 함께 하는 𝐌집합이다.
a. 𝐌은 𝒞 안의 patch들의 image들의 합집합이다.
b. 𝒞 안의 그 patch들은 overlap smoothly 매끄럽게 重疊한다, 즉, 만약 𝐗¹:𝐃¹ → 𝐌과 𝐗²:𝐃² → 𝐌가 𝒞 안의 두 patch라면,
그 composite function 𝐗̄²-1∘ 𝐗¹ 와 𝐗¹-1∘ 𝐗² 는 open domains(定義域)을 갖으며 또한 smooth하다. <- Figure I-29 참조
c. 𝐌에 두 점 𝐏와 𝐏'가 주어지면, 𝐏 ∊ 𝐗¹(𝐃¹), 𝐏' ∊ 𝐗²(𝐃²) 그리고 𝐗¹(𝐃¹) ∩ 𝐗²(𝐃²) = 𝜙(empty set)인 𝒞 안의 patch들
𝐗¹:𝐃¹ → 𝐌과 𝐗²:𝐃² → 𝐌이 존재한다 <- Hausdorf property: 𝐏, 𝐏' 근방에 안 겹치는 patch를 각기 갖을 수 있음
d. 𝒞 의 모든(every) patch와 smoothly 중첩하는 𝐌 상의 어떠한(any) coordinate patch도 𝒞 안에 있는 그 자체이다.
그러한 의미에서 the collection 𝒞 는 maximal 極大하다.
∘ domain 定義域이란 function이 정의된 가장 큰 집합을 의미합니다. 예) 𝐗²-1∘ 𝐗¹ 의 domain: 𝐗¹-1[𝐗¹(𝐃¹) ∩ 𝐗²(𝐃²)]
smooth 매끄러움이란 우리 목적을 위해 충분히 미분 가능함을 의미합니다. (보통은 최소 연속 3차의 편미분 가능함)
∘ 때때로 The collection 𝒞 는 𝐌 상의 differentiable structure, 𝒞 의 patches는 admissible patches 라고도 부릅니다.
Definition I-12 (a)(b)(c)만을 만족하는 𝐌 상의 patch들의 어떤 collection 𝒞'가 smoothly 중첩하는 모든 patch들과 결합해서
즉시 𝐌 상의 differentiable structure로 확장될 수 있다면, 𝒞'는 그 differentiable structure를 generate 生成한다고 합니다.
∘ 한 admissible patch 𝐗¹:𝐃¹ → 𝐌가 𝐏의 local coordinates 局地 座標라 부르는 유일한 ordered pair 𝐗¹-1(𝐏) = (u1, u2)와
𝐗¹(𝐃¹)의 각 점에서 결합합니다(associate). 만일 𝐗²:𝐃² → 𝐌가, 𝐗²(𝐃²)의 각 점에게 local coordinates (ū1, ū2)와 결합하는
어떤 두번째 admissible patch라면, 𝐗¹(𝐃¹) ∩ 𝐗²(𝐃²)의 점들은 두개의 local coordinates pair (u1, u2)와 (ū1, ū2)를 갖으며,
composite function 𝐗²-1∘ 𝐗¹ 와 𝐗¹-1∘ 𝐗²는 ū1와 ū2를 u1와 u2의 smooth function으로 만들며, 거꾸로도 또한 같습니다.
𝐗²-1∘ 𝐗¹ 는 ū𝑖 = ū𝑖 (u1, u2), 𝑖 = 1,2, 𝐗¹-1∘ 𝐗²는 u𝑖 = u𝑖 (ū1, ū2), 𝑖 = 1,2 [9-61ab]
이들이 바로 a change of coordinates 座標系 變換을 위한 방정식들입니다.
∘ 우리는 mapping 𝐗이라 하는 대신 가끔 단순히 (u1, u2)를 𝐌 안의 local coordinate system으로 참고하기도 할 것입니다.
앞에서 해온 것을 계속하기 위해 가끔은 local coordinates (u, v)라고 부르기도 할 겁니다. 물론, Section 3에서 의미하는
every parametriized surface는 a coordinate patch이며 그 image에다가 differential structure를 생성합니다.
∘ 만일 𝐏 ∊ 𝐗(𝐃), 𝐗(𝐃) ⊂ 𝛺인 admissible patch 𝐗:𝐃 → 𝐌이 있으면, 𝐌의 한 부분집합 𝛺를 𝐌의 한 점 𝐏의 neighborhood
近傍이라고 부릅니다. 만일 𝐌의 부분집합이 그 점들 각각의 한 neighborhood라면 open 열려있다고 부릅니다.
∘ Definition I-13
𝛺가 2-mainifold 𝐌의 한 열린 집합이라고 하자. 만일 function 𝑓 ∘ 𝐗가 𝐌 안에서 모든 admissible patch를 위해서
smooth하다면, function 𝑓:𝛺 → 𝓡도 smooth하다고 부르게 된다. 만일 𝑓:𝛺 → 𝓡이 smooth하고 𝐗:𝐃 → 𝐌가 image가
𝛺를 만나는 an admissible patch라면, ∂𝑓/∂u𝑖: 𝐗(𝐃) ∩ 𝛺 → 𝓡, 𝑖 = 1,2 를 다음과 같이 정의한다.
∂𝑓/∂u𝑖 ≡ [∂(𝑓 ∘ 𝐗)/∂u𝑖] ∘ 𝐗-1 [9-62]
즉, 𝐗(𝐃) ∩ 𝛺안의 각 점에 대해 ∂𝑓/∂u𝑖(𝐏)= [∂(𝑓 ∘ 𝐗)/∂u𝑖] ∘ (𝐗-1(𝐏)). 이것이 𝑓의 u𝑖 에 대한 partial derivative 이다.
∘ 각 𝑖에 대해 ∂/∂u𝑖는 미분 product rule을 만족함. ∴ ∂/∂u𝑖(𝑓𝑔) = 𝑓(∂𝑔/∂u𝑖) + 𝑔(∂𝑓/∂u𝑖) <- 𝑓, 𝑔의 domain이 같다고 가정
𝐗¹(𝐃¹)안의 각 점에 대해서, ∂/∂u𝑖(𝐏)[𝑓] = ∂𝑓/∂u𝑖(𝐏) <- 𝑓가 𝐏의 한 neighborhood에 정의된 smooth function라고 가정
만일 𝐗²:𝐃² → 𝐌가 또다른 admissible patch라면, overlap 𝐗¹(𝐃¹) ∩ 𝐗²(𝐃²)에서 다음의 operator 항등식을 갖습니다.
∂/∂u𝑖 = (∂ū𝑗/∂u𝑖) ∂/∂ū𝑗, 𝑖 = 1,2 ∂/∂ūk = (∂u𝑖/∂ūk) ∂/∂u𝑖, k = 1,2 <- from Eq. (61) [9-63ab]
∘ Definition I-14
m이 양의 정수라 하고 𝒪는 Em의 open 부분집합이라고 하자. 만일 𝐌 상의 𝐗-1 ∘ 𝑓이 모든 admissible patch 𝐗에 대해
smooth하다면, function 𝑓:𝒪 → 𝐌도 smooth하다고 부른다. 만일 𝒪가 open이 아니라도, 𝑓가 open domain을 갖는
약간의 smooth function인 𝒪에게만 제한이면, 우리는 𝑓:𝒪 → 𝐌가 smooth하다고 부른다. 𝐌 안의 한 curve 曲線은
한 interval에서 𝐌으로의 한 smooth function이다. 따라서 𝛂:𝐼 → 𝐌이 𝐌 안의 곡선이며 𝐗가 𝛂의 것을 포함하는 image의
한 admissible patch라면, 우리는 smooth function t와 (𝐗-1 ∘ 𝛂)(t) = (u1(t), u2(t)) 혹은 𝛂(t) = 𝐗(u1(t), u2(t))를 갖는다.
∘ 이제는 E3의 vector space stucture가 없기 때문에, 새롭게 abstract surface에 대한 tangent vector를 정의해야만 합니다.
하지만 E3 모든 vector는 해당 directional derivative operator와 결합합니다. 𝐃𝐯 = a ∂/∂x + b ∂/∂y + c ∂/∂z.
그래서 vector를 arrow가 아니라 operator로 생각하고, 먼저 velocity vector를 곡선의 directional derivative로 정의합니다.
∘ Definition I-15
𝛂:𝐼 → 𝐌가 the 2-manifold 𝐌 상의 곡선이라고 하자. 𝛂의 𝛂(t)에서의 velocity vector 는 𝛂(t)의 한 neighborhood에 정의된
모든 smooth real-valued function 𝑓를 위한 다음의 operator 𝛂'(t)이다. 𝛂'(t)[𝑓] = (𝑓 ∘ 𝛂)'(t) = d/dt [𝑓(𝛂(t))]
∘ Definition I-16
𝐏가 2-manifold 𝐌 상의 한 점이라고 하자. 만일 𝐏를 통과하며 𝐏에서 velocity vector 𝐯를 갖는 𝐌 안의 곡선이 존재하면,
𝐌의 각 smooth real-valued function 𝑓에 실수 𝐯[𝑓]를 부여하는 operator 𝐯를 𝐌 at 𝐏로의 tangent vector 라 부른다.
𝐌 at 𝐏로의 모든 tangent vector의 집합을 𝐌 at 𝐏의 the tangent plane 라고 부르며, 𝐓𝐏𝐌 이라고 표기한다.
∘ 𝛂는 𝐌 상 곡선이고 𝐗:𝐃 → 𝐌는 어떤 고정된 t를 위한 한 점 𝛂(t)의 neighborhood의 local coordinates (u1, u2)를 정의하는
한 admissble patch라고 합시다. 그러면 어떤 𝐌 상의 smooth function 𝑓를 위해서 (from multivariable chain rule),
𝛂'(t)[𝑓] = d/dt [𝑓 ∘ 𝐗(u1(t), u2(t))] = ∂(𝑓 ∘ 𝐗)/∂u𝑖 (𝐗-1∘ 𝛂(t)) du𝑖/dt = ∂𝑓/∂u𝑖 (𝛂(t)) u𝑖'(t)
따라서 𝛂'(t) = u𝑖'(t) ∂/∂u𝑖(t) 혹은 축약된 표현으로 𝛂' = u𝑖'∂/∂u𝑖 [9-64]
그러므로 한 점 𝐏 = 𝐗(u1, u2)의 어떤 tangent vector 𝐯는 ∂/∂u1(𝐏)과 ∂/∂u2(𝐏)의 선형 결합입니다.
𝐯 = v𝑖 ∂/∂u𝑖(𝐏) <- tangent vector, 계수 𝐯[u𝑖] = v𝑗, 𝑗 = 1,2 (∵ u𝑗/u𝑖 = 𝛿𝑗𝑖) [9-65]
𝐓𝐏𝐌은 이처럼 ∂/∂u1(𝐏)과 ∂/∂u2(𝐏)로 생성된(spanned) 한 vector space입니다. (두 vecter는 선형 독립하며 기저가 됨.)
∘ 두개의 local coordinates system을 적용하면, tangent vector 𝐯는 두가지 coordinate 표현(representation)을 갖습니다.
𝐯 = v𝑖 ∂/∂u𝑖(𝐏) = v̄𝑗 ∂/∂ū𝑗(𝐏) [9-66]
v̄𝑗 = v𝑖 ∂ū𝑗/∂u𝑖(𝐏), 𝑗 = 1,2, v𝑖 = v̄𝑗 ∂u𝑖/∂ū𝑗(𝐏), 𝑖 = 1,2 <- by Eq. (66) [9-67ab]
∘ Definition I-17
𝒱가 𝓡 위로 a vector space라 하자. 𝒱 상의 inner product 內積이란 𝒱 안의 각 vector 쌍 𝐯, 𝐰에 다음과 같은 속성에
따라 실수 <𝐯, 𝐰>를 할당하는 한 규칙(rule)이다.
a. <𝐯, 𝐰> = <𝐰, 𝐯> (< , >은 symmetric 對稱이다)
b. <𝑎𝐯 + 𝑎'𝐯',𝐰> = 𝑎<𝐯, 𝐰> + 𝑎'<𝐯', 𝐰> 그리고 <𝐯, 𝑎𝐰 + 𝑎'𝐰'> = 𝑎<𝐯, 𝐰> + 𝑎'<𝐯, 𝐰'> (< , >은 bilinear 二重線形이다)
c. <𝐯, 𝐯> ≧ 0 (𝒱 안의 모든 𝐯에 적용), only if 𝐯 = 𝟎, <𝐯, 𝐯> = 0 (< , >은 positive definite 陽의 定符號이다)
∘ Definition I-18
2-manifold 𝐌 상의 Riamannian metric (혹은 metric)은 𝐌의 각 tangent plane로의 inner product < , >의 한 할당이다.
각 coordinate patch 𝐗:𝐃 → 𝐌를 위하여, function 𝑔𝑖𝑗: 𝐗(𝐃) → 𝓡은 다음과 같이 정의되며, 이들은 smooth해야만 한다.
𝑔𝑖𝑗(𝐏) = <∂/∂u𝑖 (𝐏), ∂/∂u𝑗 (𝐏)>, 𝑖,𝑗 = 1,2 [9-68]
Rimannian metric으로 구비된 하나의 2-manifold를 a Riamannian 2-manifold 라고 부른다. 만약 Definition 1-17의 속성
c를 아래와 같은 더 약한 조건 c'로 대치하면 앞의 정의를 a semi-Riamannian 2-manifold 라고 부른다.
c'. 만약 𝒱 안의 모든 𝐰에게서 <𝐯, 𝐰> = 0 이라면, 𝐯 = 𝟎(< , >은 nonsigular 正則이다)
∘ Definition 1-17 (a)로부터 우리는 각 local coordinate system 𝑔𝑖𝑗 = 𝑔𝑗𝑖 (모든 𝑖,𝑗에 적용)이 됩니다. 𝑔 = det (𝑔𝑖𝑗)라고 정합니다.
만약 (ū1, ū2)가 두번째 local coordinate system이라고 하면, 우리는 유사한 function 𝑔̄𝑖𝑗 = <∂/∂ū𝑖, ∂/∂ū𝑗> 을 갖습니다.
𝑔̄mn = 𝑔𝑖𝑗 ∂u𝑖/∂ūm ∂u𝑗/∂ūn, m,n = 1,2 𝑔𝑖𝑗 = 𝑔̄mn ∂ūm/∂u𝑖 ∂ūn/∂u𝑗, 𝑖,𝑗 = 1,2 [9-69ab]
만약 주어진 점에서 tangent vector가 𝐯 = v𝑖 ∂/∂u𝑖 그리고 𝐰 = w𝑗 ∂/∂u𝑗 이면, <𝐯, 𝐰> = 𝑔𝑖𝑗v𝑖w𝑗 [9-70]
Eq. (70)의 좌변이 coordinate의 선택에 독립적이므로, 우변도 마찬가지입니다. 그러므로 다른 local coordinate system의
𝑔̄𝑖𝑗v̄𝑖w̄𝑗 도 같은 값, <𝐯, 𝐰>를 갖아야만 합니다. 바꾸어 말하면, 𝑔𝑖𝑗v𝑖w𝑗 은 an invariant 不變量입니다.
∘ 어떤 tangent vector 𝐯 를 위해서, ∥𝐯∥= <𝐯, 𝐯>1/2 라고 정의합니다. 만일 𝛂 = 𝛂(t), a ≤ t ≤ b,가 𝐌 안의 곡선이라 하면,
우리는 그 곡선의 길이를 Section 1에서 처럼, 다음과 같이 정의합니다, 𝐿 = ∫ba∥𝛂'(t)∥dt.
만일 s = s(t)가 𝛂(a)로부터 𝛂(b)까지의 곡선 거리를 나타낸다면, 𝛂(t)의 neighborhood 안의 어떤 local coordinate system을
위해서도 다음과 같이 정의됩니다. (ds/dt)2 = 𝑔𝑖𝑗 du𝑖/dt du𝑗/dt [9-71]
Eq. (71) 우측변의 invariant 표현(不變式)이 2-manifold의 the metric 計量 혹은 fundamental form 基本形式입니다.
∘ local coordinate의 각 system에서, (𝑔𝑖𝑗)를 (𝑔𝑖𝑗)의 역행렬(matrix inverse), 즉, 𝑔𝑖𝑗𝑔𝑗𝑘 = 𝛿𝑘𝑖 (𝑖,𝑘 = 1,2)라고 정의합니다. 그러면
우리는 Eqs. (36) (37)을 정의로 채택함으로써 각 coordinate system에서 Christoffel symbols 을 정의할 수 있습니다.
∘ Definition I-19
만일 s가 호의 길이인 𝛂 = 𝛂(s)가 𝐌 안의 곡선이라면, 또한 𝛂 편에 정의된 각 local coordinate system에서 다음과 같으면,
𝛂는 a geodesic 이라 부른다. d2ur/ds2 + 𝛤r𝑖𝑗 du𝑖/ds du𝑗/ds = 0, r = 1,2 [9-72]
[만일 Eq. (72)가 한 coordinate system에서 유지되면, 두 system이 중첩되는 곳에서, 다른 데에서도 물론 유지됩니다!]
∘ Theorems 1-9과 1-10은 그 증명에 있어 단지 부수적인 변경만으로 Rimannian 2-manifolds로 확장됩니다. 실제로 내재적인
매개화된 곡면을 위한 개념과 결과들도 일반적 Riamannian 2-manifolds로 확장됩니다. 이 section의 모든 기본 아이디어는
더 고차원으로 일반화합니다. 만일 모든 coordinate patch 𝐗:𝐃 → 𝐌의 domain 𝐃가 Euclidean n-space En의 부분집합이면,
Definition 1-12은 n-manifold의 정의가 됩니다. Local coordinates는 그러면 n-tuples (u1, u2 ..... un)이고, 또한 각 점 𝐏에서,
tangent "plane"은 이제 ∂/∂u1(𝐏), ∂/∂u2(𝐏) ..... ∂/∂un(𝐏)에 의해 생성된 n-dimensional tangent space 接空間입니다.
∘ 모든 지수들이 1에서 𝑛까지 값을 갖고, (𝑔𝑖𝑗)는 𝑛 x 𝑛 대칭 행렬입니다. curvature tensor 𝑅h𝑖𝑗𝑘의 독립 성분은 𝑛2(𝑛2 -1)/12개
이므로, 예를 들어 3차원에서는 6, 4차원에서는 20이 됩니다. 결과적으로 curvature를 기술하려면 한 function 𝐊(𝐏)보다는 더
많이 필요합니다. 만일 어떤 coordinate patch 𝐗:𝐃 → 𝐌를 위해서 𝐗(𝐃) 전체에서 𝑅h𝑖𝑗𝑘 = 0 (for all h,𝑖,𝑗,𝑘) 이 된다면, 𝐗(𝐃)는
flat 平平한, 즉, 국지적으로 유클리드 공간과 isometric한(等距離인) 경우입니다.
p.s. 처음 접한 미분기하학을 제가 이해할 수 있도록 저술하신 Boston College Richard Faber 교수에게 경의를 표함!
운 좋게도 현재 East Tennessee States University의 Robert Gardner 교수의 'Classnotes' (u. 7/2019)가 공개되어 있네요~
최근 동창인 재미 수학자가 이를 알려주어서 Definition I-9 증명에 도움을 받았는데, 대학원의 강의 노트라고 함.
(* 이 책에서는 tensor에 관련해서는 본격적인 논의를 않고 모든 좌표계 변환에서 불변하다는 것만 언급) |
|
|





































