|
김관석
|
2019-07-02 16:01:21, 조회수 : 1,797 |
- Download #1 : Tensor_II_2a.jpg (41.4 KB), Download : 2

h) Curl(회전): 𝛁 ⨯ 𝐮 or 𝛁 ⨯ 𝐓
𝛁 ⨯ 𝐮 = 𝐠𝑖 ∂/∂𝜉𝑖 ⨯ 𝐮 = 𝐠𝑖 ⨯ ∂𝐮/∂𝜉𝑖 = 𝐠𝑖 ⨯ 𝑢j∣𝑖 𝐠𝑗 = 𝑢j∣𝑖 𝐠𝑖 ⨯ 𝐠𝑗 = 𝝐𝑖𝑗𝑘 𝑢j∣𝑖 𝐠𝑘 <- 실제로는 단위 기저 vector로 변환하여 계산함 [14.8.1]
𝛁 ⨯ 𝐮 = 𝝐𝑖𝑗𝑘 𝑢j∣𝑖 𝐠𝑘 = (1/√𝑔)𝑒𝑖𝑗𝑘 𝑢j∣𝑖 𝐞𝑘√𝑔𝑘𝑘 = (1/√𝑔)[(𝑢3∣2- 𝑢2∣3) 𝐞1√𝑔11 - (𝑢1∣3- 𝑢3∣1) 𝐞2√𝑔22 + (𝑢2∣1- 𝑢1∣2) 𝐞3√𝑔33] [14.8.2,3]
= (1/√𝑔)[(𝑢3.2 - 𝑢2.3) 𝐞1√𝑔11 + (𝑢1.3 - 𝑢3.1)𝐞2√𝑔22 - (𝑢2.1 - 𝑢1.2) 𝐞3√𝑔33] =
∣ 𝐞1√𝑔11 𝐞2√𝑔22 𝐞3√𝑔33 ∣
1/√𝑔 ∣ ∂/∂𝜉1 ∂/∂𝜉2 ∂/∂𝜉3 ∣ [14.8.4]
∣ 𝑢1 𝑢2 𝑢3 ∣
II-5 일반 좌표계에서의 적분
a) 변환된 좌표계에서의 이중 적분: 𝑥α = 𝑥α( 𝜉1, 𝜉2 ) α = 1,2
Cartesian 좌표계에서의 scala field 𝜙(𝑥1, 𝑥2)에 대한 이중 적분은 다음과 같습니다.
∬𝐴 𝜙(𝑥1, 𝑥2)𝑑𝑥1𝑑𝑥2 = ∬𝐴̄ 𝜙̄(𝜉1, 𝜉2) 𝐽 𝑑𝜉1𝑑𝜉2, 𝐽 = ∣ ∂(𝑥1, 𝑥2)/∂(𝜉1, 𝜉2) ∣ <- Jacobian [14.9.1,2]
ex) 𝜙(𝑥1, 𝑥2) = 1, 극 좌표계에서의 이중 적분 값 구하기: 단, 0<𝜉1<1, 0< 𝜉2<𝜋/2이며, 𝑥1 = 𝜉1 cos 𝜉2, 𝑥2 = 𝜉1 sin 𝜉2 ◂ [14.9.3]
먼저 Jacobian 𝐽 = ∣ ∂(𝑥1, 𝑥2)/∂(𝜉1, 𝜉2) ∣ =
∣ ∂𝑥1/∂𝜉1 ∂𝑥2/∂𝜉1 ∣ = ∣ cos 𝜉2 sin 𝜉2 ∣ = 𝜉1 [14.9.4]
∣ ∂𝑥1/∂𝜉2 ∂𝑥2/∂𝜉2 ∣ ∣ -𝜉1sin 𝜉2 𝜉1cos 𝜉2 ∣
Scalar 불변의 법칙[II-3 (c)]에 따라 𝜙̄(𝜉1, 𝜉2) = 𝜙(𝑥1, 𝑥2) = 1 이므로,
𝐴 = ∬𝐴̄𝜙̄ (𝜉1, 𝜉2) 𝐽 𝑑𝜉1𝑑𝜉2 = ∫0𝜋/2∫01 𝜉1 𝑑𝜉1𝑑𝜉2 = (1/2-0)(𝜋/2-0) = 𝜋/4 ▮ [14.9.5]
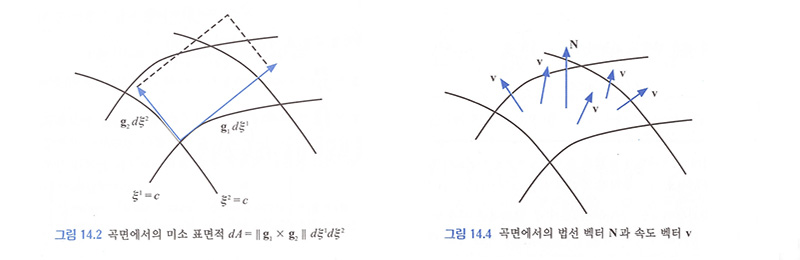
b) 곡면에서의 표면적: 𝑥𝑖 = 𝑥𝑖( 𝜉1, 𝜉2 ) 𝑖 = 1,2,3 <- 그림 14.2 참조
𝑑𝐴 = ∥𝐠1𝑑𝜉1 ⨯ 𝐠2𝑑𝜉2∥= ∥𝐠1 ⨯ 𝐠2∥𝑑𝜉1𝑑𝜉2, ∴ 𝐴 = ∬𝐴𝑑𝐴 = ∫𝐴̄∥𝐠1 ⨯ 𝐠2∥𝑑𝜉1𝑑𝜉2, ∥𝐠1 ⨯ 𝐠2∥= √ [(𝐠1 ⨯ 𝐠2) ∙ (𝐠1 ⨯ 𝐠2)] [14.9.5-8]
𝐠1 ⨯ 𝐠2 = ∂𝐱/∂𝜉1 ⨯ ∂𝐱/∂𝜉2 = (∂𝑥𝑘/∂𝜉1)(∂𝑥𝑙/∂𝜉2) 𝐞𝑘 ⨯ 𝐞𝑙 = 𝑒𝑘𝑙𝑚 (∂𝑥𝑘/∂𝜉1)(∂𝑥𝑙/∂𝜉2) 𝐞𝑚 =
∣ 𝐞1 𝐞2 𝐞3 ∣
∣ ∂𝑥1/∂𝜉1 ∂𝑥2/∂𝜉1 ∂𝑥3/∂𝜉1 ∣ [14.9.9]
∣ ∂𝑥1/∂𝜉2 ∂𝑥2/∂𝜉2 ∂𝑥3/∂𝜉2 ∣
ex) 구 좌표계에서의 표면적 구하기: 단, 0<𝜉1<𝜋, 0<𝜉2<2𝜋이며, 𝑥1 = 𝑎 sin 𝜉1 cos 𝜉2, 𝑥2 = 𝑎 sin 𝜉1 sin 𝜉2, 𝑥3 = 𝑎 cos 𝜉1 ◂
𝐠1 = ∂𝐱/∂𝜉1 = 𝑎 cos 𝜉1 cos 𝜉2 𝐞1 + 𝑎 cos 𝜉1 sin 𝜉2 𝐞2 -𝑎 sin 𝜉1 𝐞3, 𝐠2 = ∂𝐱/∂𝜉2 = -𝑎 sin 𝜉1 sin 𝜉2 𝐞1 + 𝑎 sin 𝜉1 cos 𝜉2 𝐞2 [14.9.10]
𝐠1 ⨯ 𝐠2 =
∣ 𝐞1 𝐞1 𝐞3 ∣
∣ 𝑎 cos 𝜉1 cos 𝜉2 𝑎 cos 𝜉1 sin 𝜉2 -𝑎 sin 𝜉1 ∣ [14.9.11]
∣ -𝑎 sin 𝜉1 sin 𝜉2 𝑎 sin 𝜉1 cos 𝜉2 0 ∣
= 𝑎3(sin 𝜉1)2 cos 𝜉2 𝐞1 + 𝑎2(sin 𝜉1)2 sin 𝜉2 𝐞2 + 𝑎2 sin 𝜉1 cos 𝜉1 𝐞3 → ∥𝐠1 ⨯ 𝐠2∥ = 𝑎2 sin 𝜉1
𝐴 = ∬𝐴̄ ∥𝐠1 ⨯ 𝐠2∥ 𝑑𝜉1𝑑𝜉2 = ∫02𝜋∫0𝜋 𝑎2 sin 𝜉1 𝑑𝜉1𝑑𝜉2 = 𝑎2 {-cos 𝜋 -(-cos 0)}(2𝜋 - 0) = 𝑎2(1+1)2𝜋 = 4𝜋𝑎2 ▮
c) 곡면에서의 체적
𝑑𝑉 = ∥(𝐠1𝑑𝜉1) ∙ (𝐠2𝑑𝜉2) ⨯ (𝐠3𝑑𝜉3)∥= ∥𝐠1 ∙ (𝐠2 ⨯ 𝐠3)∥𝑑𝜉1𝑑𝜉2𝑑𝜉3 [14.9.12]
𝐽 = ∣ 𝐠1 ∙ (𝐠2 ⨯ 𝐠3) ∣ = ∣ det (∂𝑥𝑖/∂𝜉𝑗) ∣ = ∣ ∂(𝑥1, 𝑥2, 𝑥2)/∂(𝜉1, 𝜉2, 𝜉3) ∣ [14.9.13]
𝑑𝑉 = 𝐽 𝑑𝜉1𝑑𝜉2𝑑𝜉3 = ∣ det (∂𝑥𝑖/∂𝜉𝑗) ∣ 𝑑𝜉1𝑑𝜉2𝑑𝜉3 [14.9.14]
𝑉 = ∭𝑣 𝑑𝑉 = ∭𝑣 ∣ det (∂𝑥𝑖/∂𝜉𝑗) ∣ 𝑑𝜉1𝑑𝜉2𝑑𝜉3 [14.9.15]
d) 변환된 좌표계에서의 삼중 적분
𝑉 = ∬𝑉 𝜙(𝑥1, 𝑥2, 𝑥2)𝑑𝑥1𝑑𝑥2𝑑𝑥2 = ∬𝑉̄ 𝜙̄(𝜉1, 𝜉2, 𝜉2) 𝐽 𝑑𝜉1𝑑𝜉2𝑑𝜉3, 𝐽 = ∣ ∂(𝑥1, 𝑥2,𝑥3)/∂(𝜉1, 𝜉2,𝜉2) ∣ [14.9.16]
ex) 구 좌표계의 구 체적 구하기: 0<𝜉1<𝑎, 0<𝜉2<𝜋, 0<𝜉2<2𝜋, 𝑥1 = 𝜉1 sin 𝜉2 cos 𝜉3, 𝑥2 = 𝜉1 sin 𝜉2 sin 𝜉3, 𝑥3 = 𝜉1 cos 𝜉2 ◂ [14.9.17]
먼저 계산에 필요한 기저 vector들을 다음처럼 구합니다. 𝐠1 = ∂𝐱/∂𝜉1 = sin 𝜉2 cos 𝜉3 𝐞1 + sin 𝜉2 sin 𝜉3 𝐞2 + cos 𝜉2 𝐞3,
𝐠2 = ∂𝐱/∂𝜉2 = 𝜉1cos 𝜉2 cos 𝜉3 𝐞1 + 𝜉1cos 𝜉2 sin 𝜉3 𝐞2 - 𝜉1sin 𝜉2 𝐞3, 𝐠3 = ∂𝐱/∂𝜉3 = -𝜉1sin 𝜉2 sin 𝜉3 𝐞1 + 𝜉1sin 𝜉2 cos 𝜉3 𝐞2 [14.9.18]
기저 vector의 삼중 내적 𝐽 = ∣ 𝐠1 ∙ 𝐠2 ⨯ 𝐠3 ∣ = ∣ det(∂𝑥𝑖/∂𝜉𝑗) ∣ =
∣ sin 𝜉2 cos 𝜉3 sin 𝜉2 sin 𝜉3 cos 𝜉2 ∣
∣ 𝜉1cos 𝜉2 cos 𝜉3 𝜉1cos 𝜉2 sin 𝜉3 - 𝜉1sin 𝜉2 ∣ = (𝜉1)2 sin 𝜉2 [14.9.19]
∣ -𝜉1sin 𝜉2 sin 𝜉3 𝜉1sin 𝜉2 cos 𝜉3 0 ∣
𝑉 = ∭𝑉̄ 𝐽 𝑑𝜉1𝑑𝜉2𝑑𝜉3 = ∫02𝜋∫0𝜋∫0𝑎 (𝜉1)2 sin 𝜉2 𝑑𝜉1𝑑𝜉2𝑑𝜉3 = {(𝑎3/3-0}{-cos 𝜋 - (-cos 0 )} (2𝜋 - 0) = (4/3)𝜋𝑎3 ▮ [14.9.20]
II-6 Differential Geometry(미분기하학)의 응용
a) 곡면에서의 길이: 공간상의 임의의 곡면이 𝐱 = 𝐱(𝜉1, 𝜉2)로 주어진다고 가정하면 그 곡면 상의 한 점에서의 미분 '𝑑𝐱'는 .
𝑑𝐱 = (∂𝐱/∂𝜉1)𝑑𝜉1 + (∂𝐱/∂𝜉2)𝑑𝜉2 이 되고, 그 곡면 상의 길이 '𝑑s'는 다음과 같이 구할 수 있습니다. [14.10.1]
(𝑑𝑠)2 = 𝑑𝐱 ∙ 𝑑𝐱 = (∂𝐱/∂𝜉1) ∙ (∂𝐱/∂𝜉1)(𝑑𝜉1)2 + 2(∂𝐱/∂𝜉1) ∙ (∂𝐱/∂𝜉2)𝑑𝜉1𝑑𝜉2 + (∂𝐱/∂𝜉1) ∙ (∂𝐱/∂𝜉2)(𝑑𝜉2)2
= 𝐸(𝑑𝜉1)2 + 2𝐹𝑑𝜉1𝑑𝜉2 + 𝐺(𝑑𝜉2)2 <- 여기서 기본 계수 (following Gauss) 𝐸, 𝐹, 𝐺 는 다음과 같이 정의합니다. [14.10.2]
𝐸 = (∂𝐱/∂𝜉1)(∂𝐱/∂𝜉1) = 𝐠1 ∙ 𝐠1 = 𝑔11, 𝐹 = (∂𝐱/∂𝜉1)(∂𝐱/∂𝜉2) = 𝐠1 ∙ 𝐠2 = 𝑔12 = 𝑔21, 𝐺 = (∂𝐱/∂𝜉2)(∂𝐱/∂𝜉2) = 𝐠2 ∙ 𝐠2 = 𝑔22 [14.10.3]
b) 곡면에서의 면적(1): 곡면이 𝐱 = 𝐱(𝜉1, 𝜉2)로 주어진 경우
𝑑𝐴 = ∥∂𝐱/∂𝜉1 ⨯ ∂𝐱/∂𝜉2∥𝑑𝜉1𝑑𝜉2 = √ [(∂𝐱/∂𝜉1 ⨯ ∂𝐱/∂𝜉2) ∙ (∂𝐱/∂𝜉1 ⨯ ∂𝐱/∂𝜉2)]𝑑𝜉1𝑑𝜉2 = √ (𝐸𝐺 - 𝐹2)𝑑𝜉1𝑑𝜉2 <- 𝐹 = 0 [14.10.4-6]
∵ ∂𝐱/∂𝜉𝑖 ↦ 𝐗𝑖; ∣𝐗1 ⨯ 𝐗2∣= ∣𝐗1∣∣𝐗2∣ sin𝜃, 𝐗1 ∙ 𝐗2 = ∣𝐗1∣∣𝐗2∣ cos𝜃, ∣𝐗1 ⨯ 𝐗2∣2 = ∣𝐗1∣2∣𝐗2∣2 sin2𝜃 = ∣𝐗1∣2∣𝐗2∣2 - ∣𝐗1∣2∣𝐗2∣2 cos2 = 𝐸𝐺 - 𝐹2
c) 곡면에서의 면적(2): 곡면이 𝜉3 = 𝑓(𝜉1, 𝜉2)으로 주어진 경우 [14.10.15]
∂𝐱/∂𝜉1 = (∂𝑥1/∂𝜉𝑖) 𝐞1+ (∂𝑥2/∂𝜉𝑖) 𝐞2+ (∂𝑥3/∂𝜉𝑖) 𝐞3 = 𝐞1+ (∂𝑓/∂𝜉1) 𝐞3; ∂𝐱/∂𝜉2 = (∂𝑥1/∂𝜉2)𝐞1+ (∂𝑥2/∂𝜉2) 𝐞2+ (∂𝑥3/∂𝜉2) 𝐞3 = 𝐞2+ (∂𝑓/∂𝜉2) 𝐞3 [14.10.16]
𝐸 = (∂𝐱/∂𝜉1) ∙ (∂𝐱/∂𝜉1) = 1 + (∂𝑓/∂𝜉1)2; 𝐹 = (∂𝐱/∂𝜉1) ∙ (∂𝐱/∂𝜉2) = (∂𝑓/∂𝜉1)(∂𝑓/∂𝜉2); 𝐺 = (∂𝐱/∂𝜉2) ∙ (∂𝐱/∂𝜉2) = 1 + (∂𝑓/∂𝜉2)2 [14.10.17]
𝑑𝐴 = √ (𝐸𝐺 - 𝐹2)𝑑𝜉1𝑑𝜉2 = √ [1 + (∂𝑓/∂𝜉1)2 + (∂𝑓/∂𝜉2)2)]𝑑𝜉1𝑑𝜉2 [14.10.18]
𝐴 = ∬𝐴 𝑑𝐴 = ∬𝐴̄ = √ [1 + (∂𝑓/∂𝜉1)2 + (∂𝑓/∂𝜉2)2)]𝑑𝜉1𝑑𝜉2 [14.10.19]
d) 곡면에서의 물리량 적분: ex) flux (流束) 𝜙 = ∬𝐴 𝐯 ∙ 𝐧 𝑑𝐴 <- 그림 14.4 참조 [14.10.20]
𝜙 = ∬𝐴 𝐯 ∙ 𝐧 ∥ 𝐠1 ⨯ (𝐠2∥𝑑𝜉1𝑑𝜉2; 𝐍 = 𝐠1 ⨯ (𝐠2, ∥𝐍∥ = ∥𝐠1 ⨯ (𝐠2∥, 𝐧 ≡ 𝐍 /∥𝐍∥ [14.10.21-24]
𝜙 = ∬𝐴 𝐯 ∙ 𝐧 𝑑𝐴 = ∬𝐴 𝐯 ∙ (𝐠1 ⨯ 𝐠2) 𝑑𝜉1𝑑𝜉2 = ∬𝐴 𝐯 ∙ 𝐍 𝑑𝜉1𝑑𝜉2 = ∭𝑉 𝛁 ∙ 𝐯 𝑑𝑉 <- 발산 정리(divergence theorem) by Gauss [14.10.25,26]
e) 기본 계수와 2종 Christoffel 기호: ex) 기본 계수 𝐸, 𝐹, 𝐺의 직교곡선 좌표계에서의 관계식 <- 𝐹 = 𝐠1 ∙ 𝐠2 = 0
𝜞111 = (∂𝐸/∂𝜉1)/2𝐸, 𝜞112 = (∂𝐸/∂𝜉2)/2𝐸, 𝜞122 = (∂𝐺/∂𝜉1)/2𝐸
𝜞211 = (∂𝐸/∂𝜉2)/2𝐺, 𝜞212 = (∂𝐺/∂𝜉1)/2𝐺, 𝜞222 = (∂𝐺/∂𝜉2)/2𝐺 [14.10.31]
그 결과를 보건데, 제2종 Christoffel 기호를 아주 간결하게 표현할 수 있는 것을 알 수 있습니다.
ex) 기본 계수를 사용하여 원통 좌표계 (𝜉1 = 𝑟, 𝜉2 = 𝜃, 𝜉3 = 𝑧)에서 2종 Christoffel 기호를 구하시오. ◂
𝐸 = 𝑔11 = 1, 𝐹 = 𝑔12 = 0, 𝐺 = 𝑔22 = 𝑟2, ∂𝐸/∂𝜉1 = 0, ∂𝐸/∂𝜉2 = 0, ∂𝐺/∂𝜉1 = 2𝑟, ∂𝐺/∂𝜉2 = 0 [14.10.32,33]
𝜞111 = (∂𝐸/∂𝜉1)/2𝐸 = 0, 𝜞112 = (∂𝐸/∂𝜉2)/2𝐸 = 0, 𝜞122 = (∂𝐺/∂𝜉1)/2𝐸 = -2𝑟/2 = -𝑟
𝜞211 = (∂𝐸/∂𝜉2)/2𝐺 = 0, 𝜞212 = (∂𝐺/∂𝜉1)/2𝐺 = 2𝑟/2𝑟2 = 1/𝑟, 𝜞222 = (∂𝐺/∂𝜉2)/2𝐺 = 0 ▮ [14.10.34]
... 일반상대성(GR)을 이해하려면 tensor와 함께 Gauss/Riemann의 미분 기하학(Differential Geometry)을 학습해야만 합니다 ...
p.s. Tensor에 관하여 처음으로 들어본 것은 1983년 당시에 친했던 울산공대 토목과 이동근 교수님으로부터였음.
Stanford 대 토목과 박사과정 유학 시 vector만 아는 상황에서 처음으로 tensor를 힘들게 수강했다는 회고담이었는데...
무려 35년이상 지난 오늘에서 제가 귀동냥만했던 바로 그 tensor를 스스로 학습하게 될 줄은 정말 몰랐음..ㅎ |
|
|





































