|
김관석
|
2019-09-04 15:16:16, 조회수 : 1,317 |
- Download #1 : gr_3_1p.jpg (71.4 KB), Download : 1

Introduction
∘ 특수 상대성 이론은 상대적 등속으로 움직이는 다른 두 관성계(inertial frame) 관찰자에 의해 측정된 이벤트의 기술에 관련합니다.
이에 의하면 우리는 다른 관성 기준계(inertial reference frame)에 관련된 움직임이외에 자기 기준계의 움직임을 말할 수 없습니다.
나아기, 전적으로 한 관성 기준계 내에서만 수행되는 어떠한 실험도 다른 기준계에 대한 움직임을 나타낼 수가 없는 것입니다.
그렇지만, 가속된 움직임은 완전히 다른 것으로서, 그 효과가 이미 느껴지기 때문입니다...예로서 자동차 운전 등... 그래서 등속의
움직임(uniform motion)은 상대적(relative)이지만, 가속된 움직임(accelerated motion)은 절대적(absolute)입니다.
∘ Einstein은 1916년 그의 '상대성의 일반 이론의 기초'(The Foundation of General Theory of Relativity) 논문에서 기존 특수 이론을
임의 기준계에까지 연장하였으며, 동시에 완전히 새로운 이론을 제안하였습니다. 다음의 몇 장(sections)에서 우리는 일반 상대성과
그 기하학적 현상의 주요 아이디어를 기술합니다. 나중의 장에서는 Chapter I 에서 개발한 수학적 도구들(mathematical tools)로써
일부의 상세들(details)을 묘사할 예정입니다.
1. The Principle of Equivalence 等價 原理
∘ Galileo(1564-1642)는 (공기 저항을 무시하면) 모든 물체는 같은 가속력을 받아 높은 건물에서 떨어뜨린 볼링공과 야구공이 동시에
떨어진다는 사실을 알았습니다. 나중에 Isaac Newton은 역학의 법칙들과 만유인력의 법칙을 발견하였습니다. Newton의 제2법칙에
물체의 움직임에 저항하는 inertial mass 慣性 質量이 나타납니다. 한편 만유인력의 법칙에서는 gravitational mass 重力 質量에
비례하는 중력을 지구가 "감지하는"(sensing) 듯이 인력(gravitational attraction)을 일으켜서 같은 가속도를 일으킵니다.
∘ Einstein은 이 두가지의 질량의 이중적 현상의 미스테리를 일반 상대성 원리의 초석이 되는 멀리 파급하는 원리로서 해결하였습니다.
우리는 다음과 같은 간단한 사고 실험(thought experiment)를 통해서 그 위대한 아이디어를 알 수 있습니다. 먼저 높은 빌딩에 있는
승강기의 로프가 끊어져서 자유 낙하하는 경우를 생각해 보면 그 안에 있는 관찰자는 중력이 없는 성간 공간에 있는 우주 정거장에
있는 것처럼 믿습니다. 즉, 자유 낙하하는 승강기는 관성 기준계로 여겨집니다.
∘ Einstein의 Principle of Equivalance 等價 原理에 의하면 낙하하는 승강기와 우주 정거장 중에서 만일 당신이 하나의 운송 수단에
탑승하였고 외부의 정보가 없다면 둘 중에 어떤 것에 탔는지를 알 수 있는 방법이 없다는 점에서 완전히 같습니다.그러므로 가속도와
중력은 절대적인 의미를 갖지 않고 자유 낙하와 중력의 부재는 관찰자의 선택(수학 용어로 좌표 시스템의 선택)에 따른 뿐입니다.
다음으로 깊은 우주 공간에서 주변 천체의 중력에서 멀리 떨어진 창문 없는 로켓이 발사되어 주변의 관성 관찰자에 대해 등가속으로
움직이고 있을 때 안의 과학자들을 상상하시기 바랍니다. 가속으로 인해서 과학자들에게는 '바닥(floor)과 천장(ceiling)'이 있습니다.
로켓안의 모든 물체는 같은 가속도로 바닥으로 낙하하므로 만일 9.8m/s2로 가속된다면 탑승자들은 지구에 있다고 여길 것입니다.
등가 원리는 본질적으로 가속의 효과와 중력의 효과를 구별할 수 있는 방법이 없읍니다. 가속도와 중력은 equivalent 等價이며,
이 등가성은 관성 질량과 중력 질량의 동일함을 말해주고 있습니다. 이의 간단한 수학적 실연(demonstration)은 다음과 같습니다.
∘ 상호 작용하는 입자 질량들 m1, m2, ... , mn이고, 𝑖 ≠𝑗, 𝐅𝑖𝑗 𝑗 번째 입자에 작용하는 𝑖 번째 입자의 힘이라면 𝐅𝑖𝑗 = - 𝐅𝑗𝑖 for all 𝑖, 𝑗
observer #1은 event를 좌표 x, y, z, t 로, observer #2는 event를 좌표 x', y', z', t' 로 측정합니다. 공간 좌표 vector는 다음과 같이
t = t'라 하고, 𝐗 = (x, y, z), 𝐗' = (x', y', z') 로 표기하며, 𝐗𝑖 observaer #1의 좌표계의 𝑖 번째 위치를 표시합니다.
만일 첫번째 관찰자기 일정한 중력장에 있다고 믿는다면은 그에게는 상대적으로 모든 입자들이 같은 vector 𝑔로 주어진다면,
m𝑖 d2𝐗𝑖 /dt2 = m𝑖 𝑔 + ∑𝑖≠𝑗 𝐅𝑗𝑖, 𝑖 =1,2,...,n <- for observer #1 [1-99]
𝐗' = 𝐗 - 1/2 (𝑔t2) <- observer #2 is moving relative to observer #1 [1-100]
differentiate twice -> d2𝐗𝑖 /dt2 = d2𝐗'𝑖 /dt2 + 𝑔
m𝑖 d2𝐗𝑖 /dt2 = ∑𝑖≠𝑗 𝐅𝑗𝑖, 𝑖 =1,2,...,n <- for observer #2 [1-101]
∘ observer #2에게는 중력장이 없다고 여기며, observer #1는 observer #2가 자유 낙하한다고 간주합니다. 두 관찰자와 두 관점은
물리적 events-역학적, 전자기적 또는 무엇이든가-의 기술들은 모두 유효한 것입니다. 이렇게 등가 원리는 관성계든 아니든 모든
frame을 같은 기초 위에 놓음으로써 상대성 원리를 확장하고 있습니다.
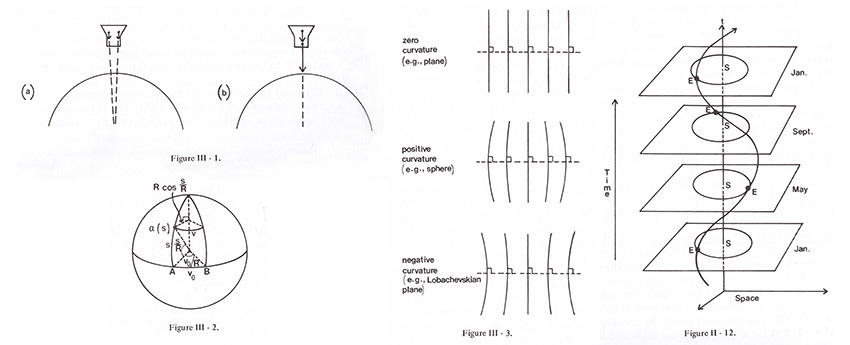
2. Gravity as Spacetime Curvature <- Figure III-1, III-2, II-12 참조
∘ 우리는 앞의 사고 실험에서 중력장이 uniform 均等하여, 모든 관성 관찰자에게 상대적으로 모든 낙하하는 대상의 가속도가
일정한(constant) 크기와 방향을 갖는다고 가정하였습니다. 하지만 실제로는 중력에 의한 가속도는 점과 점마다 차이가 있습니다.
예를 들면 지구 표면으로 자유 낙하하는 우주선 캡슐에 대해 상대적으로 처음부터 정지해 있는 두 시험 입자들을 생각하십시요.
Figure III-1 (a) 에서처럼 이 두 입자의 분리선이 수평하다, 즉 캡슐로부터 지구 중심으로의 방향에 직교하다고 상상하기 바랍니다.
양 입자들이 지구의 중심으로 향하고 있기 때문에 이들 간의 간격은 반드시 줄어드는데, 실제로 그 비율이 점차 증가하게 됩니다.
마찬가지로 만일 그 입자들의 분리가 수직적이라면, 지구에 가까운 입자는 약간 큰 가속도를 받게되어 점차 간격이 커질 것입니다. .
∘ 중력의 tidal effect 潮汐 效果라고 부르는 이 효과는 지구의 중력장의 비균질성-중력의 당김이 점점마다 다름-에 의한 것입니다.
지구적인 스케일로는 조석 효과는 대양의 조석의 원인이 되지만, 우리의 우주선 캡슐의 스케일에서는 이 효과들은 작습니다.
결과적으로 만일 이 두 입자들의 처음부터 꽤 가깝고, 만일 우리가 그 움직임을 짧은 시간 동안에 관찰하면 그들의 상대적 가속도는
너무 작아서 우리의 측정 도구로는 탐지할 수 없게될 것입니다. 다른 말로, 충분히 작은, 자유 낙하하는 우주선 캡슐은, 충분히 작은
시간 간격에서는, 처음 근사치로서는 하나의 관성계(inertial frame)입니다. 등가 원리는 이제 다음과 같은 형식이 됩니다.
' 각 시공간의 점(즉, 이벤트)과 주어진 정확성의 정도를 위해서는 어떤 공간의 영역과 어떤 시간의 간격에서(이벤트들의 충분하게
작은 시공간 neighborhood에 있어서), 중력 효과는 무시할 수 있으며, 그 frame은 명시된 정확성 정도 만큼 관성적(inertial)이다.'
∘ 이러한 기준계(reference frame)는 locally inertial frame 局所 慣性界 (이벤트들에서)라고 부르며, 그 frame 속에서 정지한 자유
낙하하는 관찰자를 locally inertial observer 局所 慣性 觀察者라고 부릅니다. locally inertial frame에 상대적인 등속으로 움직이는
어떠한 frame도 논의되는 시공간 점의 neighborhood 안에서는 역시 locally inertial frame인 것입니다.
∘ 중력의 조석 효과(비균일성)으로 돌아가보면, 자유 낙하하는 시험 입자들의 상대적 가속도는 구체에 쉽게 시각화 할 수 있는 순수한
기하학적 analogue를 갖습니다. 지구 적도에서 근접한 곳에서 분리된 여정을 가는 두 여행자 (Figure III-2 A와 B)를 상상하십시요.
d2v /ds2 + v /R2 = 0, d2v /ds2 + 𝐊 v = 0 <- the equation of geodesic deviation or Jacobi, 𝐊: Gauss curvature [2-102]*
예를 들면 Figure III-3과 같이 negative curvature의 표면에서는 처음에 평행한(initially parallel) geodesic들이 서로 간 멀어집니다.
∘ (a) 비균질한 중력장에서의 자유 입자들의 상대적인 가속도와 (b) 휘어진 곡면에서 근방의 geodesic들의 변화하는 분리 사이에는
모호한 유사성 이상이 있습니다. Einstein은 그의 등가 원리로부터 추론하여서, 중력은 Newton이 믿었던 것 같은 힘(force)이 아니라
시공간의 curvature라고 결론을 내렸습니다. 그 curvature의 원천은 물질 자체입니다. 바로 자석이 주변에 자기장 거는 것과 같이
물질 객체도 주변 시공간을 왜곡시키거나 휘게하는 중력장을 창조합니다. Einstein은 자유 입자들은 중력장의 휘어진 시공간에서
반드시 geodesic들을 따른다는 가설을 세웠습니다.
∘ 이 geodesic들은 4차원의 곡선임을 깨닫는 것아 중요합니다. Figure II-12은 우리가 지구 궤도의 시공간 다이아그램 스케치입니다.
만일 시간과 거리의 축척을 같은 단위인 cm로 그린다면 지구의 world-line은 104의 거대한 factor를 갖는 축으로의 타원 나선으로
스케치될 것니다. 그렇다면 그것은 실용적으로는 직선과 구별할 수 없습니다. 그러므로 이 world-line은 geodesic이며 늘어난 나선은
결국은 거의 휘어지지 않았음을 알게되는 것은 놀라운 일이 아닙니다. 실제로 한 geodesic이라는 의미에서는 완전히 직선입니다,
다이아그램에서는 휘어진 것처럼 look 보일 수 있습니다만, curvature를 갖는 것은 world-line이 아니라 시공간의 주변 지역입니다.
(우리 다이아그램은 직교 좌표계로 표현되었지만, 시공간의 휘어진 지역에서는 직교 좌표계가 설정되지 않고, Cartesian 좌표계 처럼
국소 근사(local approximation) 이외에는 적용될 수 없습니다. 크게는 곡면 좌표계(curvilliniear coordinates)가 요구됩니다.)
∘ 이제 locally inertial frame 局所 慣性界의 관점에서의 추가의 수학적 공식화(formulation)로서 이 장의 결론을 맺습니다.
η𝑖𝑗 = {(1, if 𝑖 = 𝑗 = 0), (-1, if 𝑖 = 𝑗 = 1, 2, or 3), (0, if 𝑖 ≠ 𝑗)}, (η𝑖𝑗): the matrix of Lonentz metric.
d𝜏2 = η𝑖𝑗du𝑖du𝑗 = (du0)2 - (du1)2 - (du2)2 - (du3)2 <- locally initial frame에서 중력 효과는 무시할 수 있음. [2-103]
d𝜏2 = 𝑔𝑖𝑗du𝑖du𝑗, 𝑔𝑖𝑗(𝐏) = η𝑖𝑗, ∂𝑔𝑖𝑗/ ∂u𝑘 (𝐏) = 0, for all 𝑖,𝑗,𝑘 = 0,1,2,3 <- locally Lorentzian coordinate system at 𝐏 [2-104,105]
Eqi.(104)는 metric이 𝐏에서의 Lorentzian 임을 명기하고, Eq. (105)는 𝑔𝑖𝑗가 𝐏의 작은 neighborhood에서 작은 변화율
갖으므로 각각 η𝑖𝑗 아주 조금 다를 뿐이라는 것을 암시합니다. 수식으로 표현하면, d𝜏2 ≈ η𝑖𝑗du𝑖du𝑗.
우리가 𝐏에서 움직일 때 d𝜏2가 Lorentzian metric η𝑖𝑗du𝑖du𝑗로부터 벗어나는 정도는 중력의 비균질성과 물리적으로 일치합니다.
수학적으로는, 앞으로 우리가 보게 되듯이, 그것은 시공간의 휘어짐(the curvture of spacetime)과 일치합니다!
p.s. Richard L. Faber Differential Geometry and Relativity Theory (Marcel Deckker 1983) Chapter III.
특수 상대론(SR)은 앞에서 이미 기술했으므로 Chapter II Special Relativity는 연계 부분만 리뷰하여 기술함.
필요 시에는 미 ETSU 대 Robert Gardner 교수의 대학원 강의 'Classnotes' (u. 7/2019)를 참조하기 바람.
* Figure III-2 도해를 참고하면 어렵지 않게 증명할 수 있음. |
|
|





































