|
김관석
|
2019-09-04 15:20:26, 조회수 : 566 |
- Download #1 : gr_3_3p.jpg (49.2 KB), Download : 1

* Special Relativity Review
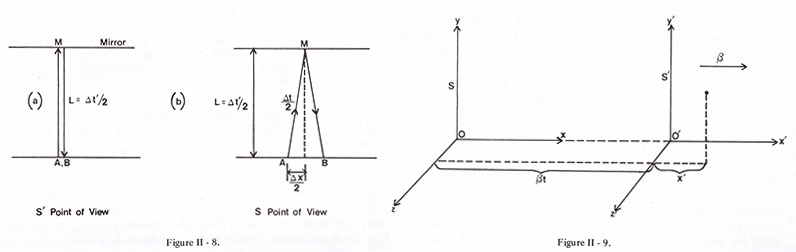
∘ Invariance of the Interval <- Figure II-8 참조
Laboratory 관찰자 S와 S에 대해 상대적으로 속도 β로 움직이는 rocket 관찰자 S'를 가정한 사고 실험에서 Figure 2-8처럼
로켓 안의 좌표 원점에서 y'축으로 거리 L만큼 떨어진 거울을 향해서 빛의 beam을 비추면 반사하여 𝛥t' = 2L 빛 이동시간 후에
되돌아옵니다. rockert 관찰자는 원점에 있는 한 single clock 으로 emmision(event A)와 reception(event B) 사이의
time interval 𝛥t'를 측정할 수 있습니다. 그렇지만 laboratory 관찰자 S는 이 interval 동안 rocket과 그 속의 거울이 우측으로
거리 𝛥x를 움직이는 것을 봅니다. 따라서 관찰자 S에게 빛은 rockect 관찰자에게 인식된 것보다 긴 figur 2-8(b)의 A→M→B를
이동하였습니다. (∆AMB의 높이는 L이며, 상대적 운동의 방향에 수직인 길이는 불변합니다.) 광속은 두 관찰자에게 동일합니다.
𝛥t'/2 = [(𝛥t/2)2 - (𝛥x/2)2]1/2 or (𝛥t')2 = (𝛥t)2 - (𝛥x)2 [II-77]
𝛥t' = (1 - β2)1/2 𝛥t or 𝛥t = (1 - β2)1/2 𝛥t' <- S에 대한 S'의 속도 β = 𝛥x/𝛥t, 후자는 S에서 event A, B가 일어날 경우 [II-78]
(𝛥t')2 - (𝛥x')2 = (𝛥t)2 - (𝛥x)2 <- 𝛥x' = 0 이므로 [II-79]
𝛥𝜏 = [(𝛥t)2 - (𝛥x)2]1/2 = [(𝛥t')2 - (𝛥x')2]1/2 <- interval between event A and B: 좌표계의 변경에 invariant 不變함. [II-80]
𝛥𝜏 = [(𝛥t)2 - (𝛥x)2 - (𝛥y)2 - (𝛥z)2]1/2 <- timelike interval: proper time between the events [II-81]
𝛥𝜎 = [(𝛥x)2 + (𝛥y)2 + (𝛥z)2 - (𝛥t)2 ]1/2 <- spacelike interval: proper distance between the events [II-82]
L' = β 𝛥t' = β 𝛥t (1 - β2)1/2 = L (1 - β2)1/2 <- L: 정지 상태의 물체 길이, L': 등속 β로 움직이는 물체 길이(축소됨) [II-83]
∘ The Lorentz Transformation <- Figure II-8, II-9 참고
x = a11x' + a12y' + a13z' + a14t', y = y', z = z', t = a41x' + a42y' + a43z' + a44t' <- x = x' + βt [II-84]
x = a11x' + a14t', t = a41x' + a44t' <- 공간의 등방성(isotropy)으로 인해서 a12 = a13 = 0, a42 = a43 = 0 II-85,86]
x = a11x' + β (1 - β2)-1/2 t' <- S' 원점이 when x' = 0, x = β t, t = (1 - β2)-1/2 t' [II-87]
t = a41x' + (1 - β2)-1/2 t' <- 위와 같은 방식으로 [II-88]
[a41x' + (1 - β2)-1/2 t']2 - [x = a11x' + β (1 - β2)-1/2]2 = t'2 - x'2 <- eq. (87)(88) and t2 - x2 = t'2 - x'2
(a412 - a112) x'2 + 2(1 - β2)-1/2 (a41 - β a11) t' x' + t'2 = t'2 - x'2, ∴ (a412 - a112) = -1, a41 - β a11 = 0
x = (x' + β t')(1 - β2)-1/2, y = y', z = z', t = (β x' + t')(1 - β2)-1/2 <- called as Lorentz Transformation [II-89]
x' = (x - β t')(1 - β2)-1/2, t = (-β x' + t')(1 - β2)-1/2 <- the inverse transformation: β replaced by -β [II-90]
𝛥x = (𝛥x' + β 𝛥t')(1 - β2)-1/2, 𝛥t = (β𝛥x' + 𝛥t')(1 - β2)-1/2 <- for pair of envents [II-91]
∘ Lorentz Geometry
L(𝛼) = ∫𝛼 ds = ∫𝛼 [(dx)2 + (dy)2 + (dz)2]1/23 in 𝔼3; L(𝛼) = ∫𝛼 d𝜏 = ∫𝛼 [(dt)2 - (dx)2 - (dy)2 - (dz)2]1/2 in 𝓡4 [II-92]
(d𝜏)2 = (dt)2 - (dx)2 - (dy)2 - (dz)2]1/2 <- proper time of 𝛼 or spacetime length; 𝓡4: Minkowski space [II-93]
Lorentz coordinates : 관성 관찰자가 사용하는 거리 측정과 동기화된 시계(synchronized clock)의 관점에서 정의된 좌표계
u0 = u0(t, x, y, z), u1 = u1(t, x, y, z), u2 = u2(t, x, y, z), u3 = u3(t, x, y, z) <- smooth, non-singular Jacobian matrix {II-95]
(d𝜏)2 = 𝑔𝑖𝑗 du𝑖 du𝑗; If d2ur/(d𝜏)2 + 𝛤r𝑖𝑗 du𝑖/d𝜏 du𝑗/d𝜏 = 0, r = 0,1,2,3, a curve u𝑖(𝜏), 𝑖 = 0,1,2,3 is called geodesic [II-96,97]
이처럼 일반화된 형식의 표현에 의해서, Chapter I 에서와 같이 Christoffel 기호와 curvature tensor를 정의할 수 있습니다!
6. Geodesics(측지선)
∘ 시공간은 다음의 metric form을 갖는 semi-Riemannian 4-manifold로 파악됩니다. (d𝜏)2 = 𝑔𝜇𝜈dx𝜇dx𝜈, in (x0, x1, x2, x3)
만일 <𝐯, 𝐯> = 𝑔𝜇𝜈du𝜇du𝜈 가 각각 양, 영, 음일 때, vector 𝐯 = v 𝜇 ∂/∂𝐱𝜇 를 각각 timelike, lightlike, spacelike 라고 부릅니다.
∘ Definition III-1
만일 한 시공간 곡선(spacetime curve) 𝛂가 다음을 만족하는 한 paramatrization x𝜆(𝜌)를 갖는다면, 그것은 한 geodesic이다.
d2x𝜆/(d𝜌)2 + 𝛤𝜆𝜇𝜈 dx𝜇/d𝜌 dx𝜈/d𝜌 = 0, 𝜆 = 0,1,2,3 <- This definition is independent of a choice of coordinate system. [6-120]
∘ 방정식 (120)은 다음 함수가 상수임을 암시합니다. 즉, <𝛂', 𝛂'> = (d𝜏/d𝜌)2 = 𝑔𝜇𝜈 dx𝜇/d𝜌 dx𝜈/d𝜌 = C2 <- C2: constant
C2가 각각 양, 영, 음일 때, 𝛂를 각각 timelike, lightlike, spacelike 라고 부릅니다.
만일 𝛂가 timelike이라면, 𝜌 = a𝜏 + b (a, b는 실수)로 추론합니다. 우리는 𝛂가 "future-directed"되도록, a>0로 가정할 것입니다.
-> 그러면 𝛂를 proper time으로써 간단하게 재매개화(reparamatrization)함으로써 Eq. (120)의 𝜌를 𝜏로 대치할 수 있습니다.
만일 𝛂가 lightlike이라면, 𝜏는 𝛂를 따라 일정하고, <𝛂', 𝛂'> = 0 이므로, 우리는 proper time을 매개변수로 사용할 수 없습니다.
만일 𝛂가 spacelike이라면, d𝜏/d𝜌는 허수가 되고 곡선은 proper distance로 재매개화하여 𝜌 = a𝜎 + b가 됩니다.
-> 아무런 신호나 물질 대상도 spacelike 경로로 이동할 수 없기 때문에 우리는 이 경우는 필요하지 않습니다.
그래서 만일 곡선 𝛂가 각 점에서 <𝛂', 𝛂'>가 양수이라면, timelike 이라고 부릅니다.
∘ Theorem III-2
𝛂가 양끝점 간의 시공간 거리(proper time 간격)을 극치화하는(extremize) timelike 곡선이라고 하면, 𝛂는 한 geodesic이다.
∘ Theorem III-3
한 event 𝐏와 𝐏에서의 non-zero vector 𝐯가 주어진다면, 𝛂(0) = 𝐏 그리고 𝛂'(0) = 𝐯인 유일한 geodesic 𝛂(𝜌)가 존재한다. |
|
|





































