|
김관석
|
2020-04-16 07:13:39, 조회수 : 590 |
- Download #1 : Hobson_etal_GR_2006s.jpg (106.7 KB), Download : 7

Variational approach to GR (S.6-8) (S.9-12)
19. A variational approach to general relativity (일반상대성에의 한 변분적 접근)
19.1 Hamilton's principle in Newtonian mechanics (Newton 역학에서의 Hamilton의 원리)
∘ Hamiiton의 원리는 시간 𝑡1의 configuration으로부터 시간 𝑡2에서의 다른 것으로 이동하는 데에 있어서 다음의 작용을 정상적으로 만드는 하나의 계를
제시한다.
𝑆 = ∫𝑡2𝑡1 𝐿(ua, ůa, 𝑡) 𝑑𝑡. (a = 1, 2,..., n) (19.1) **
Lagrangian 𝐿은 (어떤 참고 상황에 대해서) 운동에너지 𝑇와 potential energy 𝑉의 용어로, 𝐿 = 𝑇 - 𝑉 식에 의해 정의된다. 여기서 𝑉는 ua(그리고 혹은 𝑡)
의 함수이나 ůa의 함수는 아니다. Section 3.19에서 정의한 것처럼 좌표계는 한 configuration 공간 을 선 요소인 𝑑𝑠2 = 𝑔ab𝑑𝑢a𝑑𝑢b 로 정의한다. 예를
들면, 질량 𝑚의 입자를 위한 Lagrangian은 다음과 같이 쓸 수 있다.
𝐿 = 𝑇 - 𝑉 = (1/2)𝑚𝑔ab𝑑ůa𝑑ůb - 𝑉 (19.2)
∘ 일반적 표현 (19.1)로 돌아가면 우리는 configuration 공간에서의 궤도안의 한 임의 변분을 다음과 같이 고려하도록 하고,
ua(t) → u'a(t) = ua(t) + 𝛿ua(t)
작용 속의 해당하는 변분 𝛿𝑆가 사라지도록 요구하도록 하라.* 끝점 𝑡1과 𝑡2에서 𝛿ua(t) = 0 라고 가정하면 Lagrangian 𝐿은 다음의 Euler-Lagrangian(EL)
방정식을 만족하여야 한다.
∂𝐿/∂𝑢a - (𝑑/𝑑𝑡)(∂𝐿/∂ůa) = 0, (a = 1, 2,..., n).
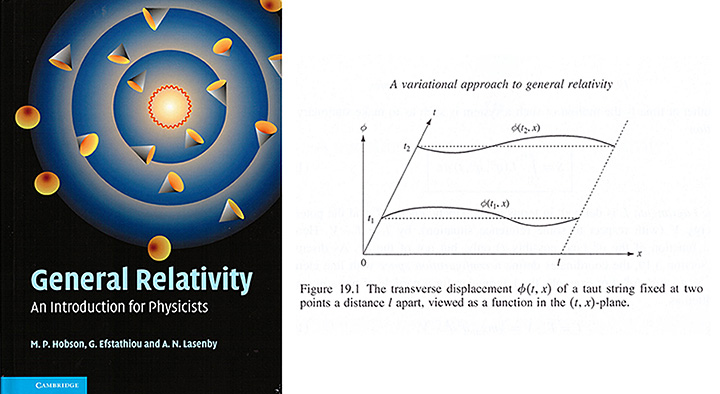
∘ Hamiliton의 원리는 불연속 입자의 관념으로부터 연속 system으로 연장될 수 있다. 두 고정돤 점 𝑥 = 0 과 𝑥 = 𝑙 사이에 잡아당겨진 한 유연한 끈을
고려해 보도록 하자. 이 경우에는, 우리는 다시 한 독립된 시간 좌표 𝑡를 갖지만, 이제는 연속체의 맥락에서고 거기서 ua(t)는 그 끈을 위치와 시간의
한 함수로서 횡단하는 이동을 표현하는 연속 변수 𝜙(𝑡, 𝑥)가 된다. (위의 Figure 19.1을 보라). 결과적으로, 𝑇와 𝑉를 위한 표현은 그 label a위에서
합이기보다는 𝑥 위에서의 적분들이 된다. 만일 𝜌(𝑥)와 𝜏(𝑥)가 국지 선 밀도와 끈의 장력이라면 작은 이동에서의 그 끈들의 운동에너지와 potential
energy는 다음으로 주어진다.
𝑇 = ∫𝑙0 1/2 𝜌(∂𝜙/∂𝑡)2 𝑑𝑥 그리고 𝑉 = ∫𝑙0 1/2 𝜏(∂𝜙/∂𝑥)2 𝑑𝑥.
이리하여, 작용 (19.1)은 다음이 된다.
𝑆 ≡ ∫𝑡2𝑡1∫𝑙0 𝓛 𝑑𝑥𝑑𝑡 = ∫𝑡2𝑡1∫𝑙01/2 [𝜌(∂𝑡𝜙)2 - 𝜏(∂𝑥𝜙)2] 𝑑𝑥𝑑𝑡, (19.3)
여기 첫번째 등식에서 우리는 Lagrangian 밀도 𝓛 을 정의했고 마지막 표현에서는 우리는 약기(略記) ∂𝑡 = ∂/∂𝑡 와 ∂𝑥 = ∂/∂𝑥 를 채용했다. 이제 다음
형식의 함수 𝜙에서의 한 임의 변분을 고려하도록 하자.
𝜙(𝑡, 𝑥) → 𝜙'(𝑡, 𝑥) = 𝜙(𝑡, 𝑥) + 𝛿𝜙(𝑡, 𝑥). (19.4)
이것은 다음 식에 의해 작용 (19.1)의 한 변분에 도달한다.
𝛿𝑆 = ∫𝑡2𝑡1∫𝑙0 [{∂𝓛/∂(∂𝑡𝜙)}𝛿(∂𝑡𝜙) + {∂𝓛/∂(∂𝑥𝜙)}𝛿(∂𝑥𝜙)] 𝑑𝑥𝑑𝑡. (19.5)
(19.4)로부터, 𝛿(∂𝑡𝜙 = ∂𝑡(𝛿𝜙) 그리고 𝛿(∂𝑥𝜙 = ∂𝑥(𝛿𝜙) 임을 즉시 유념한다. 이것들을 (19.5)에서 치환하고 한 곱의 미분을 위한 Leibnitz의 법칙-
부분 적분법-을 사용하면, 우리는 다음처럼 쓸 수 있다.
𝛿𝑆 = 𝛿𝑆b - [∂𝑡{∂𝓛/∂(∂𝑡𝜙)} + ∂𝑥{∂𝓛/∂(∂𝑥𝜙)}] 𝛿𝜙𝑑𝑥𝑑𝑡. (19.6)
여기서 '경계'(혹은 '곡면') 용어인 𝛿𝑆b는 다음처럼 사라지고 ... (중략) ... 우리는 다음을 얻는다.
∂𝑡[∂𝓛/∂(∂𝑡𝜙)] + ∂𝑥[∂𝓛/∂(∂𝑥𝜙)] = ∂𝑡(𝜌∂𝑡𝜙) - ∂𝑥(𝜏∂𝑥𝜙) = 0,
여기서, 첫번째 등식에서, 우리는 𝓛의 도함수를 ∂𝑡𝜙와 ∂𝑥𝜙에 대해서 산정하였다. 만일, 닷붙여서, 𝜌와 𝜏가 𝑥나 𝑡에 의존하지 않는다면,
∂2𝜙/∂𝑥2 = (1/𝑐2)∂2𝜙/∂𝑡2,
여기서, 𝑐2 = 𝜏/𝜌. 이것은 한 팽팽하고 균등한 끈의 작은 횡단 진동을 위한 -Newton 역학과 동일한- 파(wave) 방정식이다.
19.2 Classical field theory and the action (고전적 장이론과 그 작용)
(19.3)의 유추에 의해서, 일반적 사차원 다양체에 정의된 field 한 집합을 위한 작용 𝑆 는 Lagragian 밀도라 불리는 어떤 함수 𝓛의 한 적분 형태를
가져야 하며, 그 함수는 시공간의 어떤 사차원 지역 𝓡의 field들 𝚽a과 그 일차(그 이상도 가능)도함수들 위에 형성된다. 그래서 우리는 다음의 작용
적분을 취한다.
𝑆 = ∫𝓡 𝓛(𝚽a, ∂𝜇𝚽a, ∂𝜇∂𝜈𝚽a, ...) 𝑑4𝑥, (19.7)
여기서 𝑑𝑥4는 좌표 미분들 𝑑𝑥0𝑑𝑥1𝑑𝑥2𝑑𝑥3의 곱을 표시한다. 한편 불변량인 부피 요소인 𝑑4𝑉 = √-𝑔 𝑑4𝑥 이고, 여기서 𝑔는 그 좌표계의 계량텐서의
determinant이다. (엄밀한 추론은 Dirac의 GR '20. Tensor densities'를 참고하라.) 그래서 작용 (19.7)은 다음의 형태로 쓸 수 있다.
𝑆 = ∫𝓡 𝐿√-𝑔 𝑑4𝑥,
여기서 field Lagrangian 𝐿을 도입하고, 그것은 다음에 의해 Lagrangian 밀도 𝓛에 분명하게 관련된다.
𝓛 = 𝐿√-𝑔. (19.8)
그래서 어떤 사차원 다양체에 정의된 고전적 장의 한 집합을 위한 작용은 다음으로 쓰여질 수 있다.
𝑆 = ∫𝓡 𝐿(𝚽a, ∂𝜇𝚽a, ∂𝜇∂𝜈𝚽a, ...)√-𝑔 𝑑4𝑥,
여기서 𝐿은 시공간 위치의 한 scalar 함수이다. 우리는 Lagrangian 밀도 𝓛가 한 scalar 밀도라서 좌표계의 변환 시 불변임을 최종적으로 주목한다.
19.3 Euler-Lagrange equation(Euler-Lagrange 방정식)
우리는 이제 다음 형태의 field들에서 작은 변분아래서 작용이 정상인 혹은 불변량임을 요구함으로써 그 filed들 𝚽a들의 방정식을 유도합니다.
𝚽a(𝑥) → 𝚽'a(𝑥) = 𝚽a(𝑥) + 𝛿𝚽a(𝑥). (19.9)
단순성을 위해서, 우리는 장이론이 국지적이라고 가정을 하며, 이는 그 작용에는 이차나 삼차도함수가 나타나지 않음을 뜻합니다. 그래서 우리는
다음의 변분만이 필요합니다.
∂𝜇𝚽a → ∂𝜇𝚽'a = ∂𝜇𝚽a + ∂𝜇(𝛿𝚽a). (19.10)
다음의 사용을 위해서 우리는 (19.9)의 정의로부터 𝛿 연산자가 교환적임에 주목해야 한다. 왜냐하면 그것은 다음의 증명에 의해서이다,
∂𝜇(𝛿𝚽a) = ∂𝜇(𝚽'a - 𝚽a) = ∂𝜇𝚽'a - ∂𝜇𝚽a = 𝛿(∂𝜇𝚽a). (19.11)
(19.8)과 𝑆 → 𝑆 + 𝛿𝑆 로부터 다음이 된다.
𝛿𝑆 = ∫𝓡 𝛿𝓛 𝑑4𝑥 = ∫𝓡 [(∂𝓛/∂𝚽a)𝛿𝚽a + {∂𝓛/∂(∂𝜇𝚽a)}𝛿(∂𝜇𝚽a)] 𝑑4𝑥. (19.12)
여기서 두번째 피적분 항은 (19.11)과 부분 적분에 의해 다음으로 쓸 수 있다..
∫𝓡 {∂𝓛/∂(∂𝜇𝚽a)}∂𝜇(𝛿𝚽a) 𝑑𝑥4 = ∫𝓡 ∂𝜇[{∂𝓛/∂[(∂𝜇𝚽a)}𝛿𝚽a] 𝑑𝑥4 - ∫𝓡 ∂𝜇[∂𝓛/∂(∂𝜇𝚽a)]𝛿𝚽a 𝑑4𝑥.
우리가 허용할 수 있는 변분 𝛿𝚽a이 경계 ∂𝓡에서 사라지도록 처음과 끝 값을 0으로 한정하면 첫 항의 적분은 사라지고, 따라서 (19.2)는 다음이 된다.
𝛿𝑆 ≡ ∫𝓡 (∂𝓛/∂𝚽a)𝛿𝚽a 𝑑4𝑥 = ∫𝓡 [∂𝓛/∂𝚽a - ∂𝜇{∂𝓛/∂(∂𝜇𝚽a)}]𝛿𝚽a 𝑑4𝑥.
여기서 우리는 field 𝚽a에 대한 Lagrangian 밀도의 변분적 도함수 ∂𝓛/∂𝚽a)𝛿𝚽a를 정의한다. 만일 우리가 그 작용이 정상적이기를, 그래서 임의의
변분 𝛿𝚽a아래에서 𝛿𝑆 = 0, 우리는 이렇게 다음 식을 필요로 한다.
∂𝓛/∂𝚽a = ∂𝓛/∂𝚽a - ∂𝜇[∂𝓛/∂(∂𝜇𝚽a)] = 0. (19.13)
이들은 작용 𝑆 = ∫𝓡 𝓛 𝑑4𝑥 로 정의된 (국지적) 장이론의 장방정식에 대응하는 Euler-Lagrangian (EL)방정식이다. 만일, 덧붙여서, Lagrangian 밀도가
이차도함수나 고차도함수에 의존한다면 위의 유도가 곧바로 일반화된다. 예를 들면, 만일 이차도함수가 나타나면 다음 식을 얻는다.
∂𝓛/∂𝚽a)𝛿𝚽a = ∂𝓛/∂𝜇𝚽a)𝛿𝚽a - ∂𝜇[∂𝓛/∂(∂𝚽a)] + ∂𝜇∂𝜈[∂𝓛/∂(∂𝜇∂𝜈𝚽a)] = 0, (19.14)
이것은 변분 𝛿𝚽a와 그 일차도함수가 경계 ∂𝓡에서 사라질 경우이다.
19.4 Aternative form of Euler-Lagrange equation (Euler-Lagrange 방정식의 대안 형식)
∘ 앞의 (19.13) 형태이거나, 혹은 일반화 된 고차도함수의 field들의 EL 방정식은 주어진 작용에 대해 장방정식을 결정하는 직접적인 수단을 제공한다.
특히, 앞으로 나올 중력 작용으로부터 Einstein 장방정식들을 유도할 때 metric tensor 𝑔𝜇𝜈의 성분들이 변화하는 field들 𝚽a에서도 역시 유효하다.
∘ 그럼에도 불구하고, 만일 field들 𝚽a이 metric tensor의 성분이 아니면, Lagrange 밀도의 √-𝑔 인자의 존재가 EL 방정식 (19.13)를 형성한다. 그 경우
field Lagragian 𝐿은 종종 𝚽a과 그 공변 도함수 𝛁𝜇𝚽a로 쓸 수 있다. 이제 앞과 유사한 해설은 생략하고 EL 방정식의 유도를 반복해 보기로 하자.
𝑆 = ∫𝓡 𝐿(𝚽a, 𝛁𝜇𝚽a, 𝛁𝜇𝛁𝜈𝚽a, ..., 𝑔𝜇𝜈,∂𝜎𝑔𝜇𝜈, ...)√-𝑔 𝑑4𝑥. (19.15)
𝛁𝜇𝚽a → 𝛁𝜇𝚽'a = 𝛁𝜇𝚽a + 𝛁𝜇(𝛿𝚽a). (19.16)
𝛿𝑆 = ∫𝓡 𝛿𝐿√-𝑔 𝑑4𝑥 = ∫𝓡 [(∂𝐿/∂𝚽a)𝛿𝚽a + {∂𝐿/∂(𝛁𝜇𝚽a)}𝛿(𝛁𝜇𝚽a)]√-𝑔 𝑑4𝑥. (19.17)
∫𝓡 {∂𝐿/∂(𝛁𝜇𝚽a)}𝛁𝜇(𝛿𝚽a)√-𝑔 𝑑𝑥4 = ∫𝓡 𝛁𝜇[{∂𝐿/∂[(𝛁𝜇𝚽a)}𝛿𝚽a]√-𝑔 𝑑𝑥4 - ∫𝓡 𝛁𝜇[∂𝐿/∂(𝛁𝜇𝚽a)]𝛿𝚽a√-𝑔 𝑑4𝑥. (19.18)
∫𝓡 (𝛁𝜇𝑉𝜇)√∣𝑔∣ 𝑑4𝑥 = ∫∂𝓡 𝑛𝜇𝑉𝜇√∣𝛾∣ 𝑑3𝑦, (19.19) [발산 정리(divergence theorem)를 사용]
여기서 𝑉𝜇는 한 임의 vector field, 𝛾는 좌표 𝑦𝑖의 경계에서의 유도된 metric의 determinant 그리고 𝑛𝜇는 그 경계의 한 단위 법선이다. 이것을 (19.18)의
우측 첫 항에 적용해서, ∂𝓡에서 변분 𝛿𝚽a이 사라지도록, 즉 그 항이 0이 되도록 한정한다.
𝛿𝑆 ≡ ∫𝓡 (∂𝐿/∂𝚽a)𝛿𝚽a√-𝑔 𝑑4𝑥 = ∫𝓡 [∂𝐿/∂𝚽a - 𝛁𝜇{∂𝐿/∂(∂𝜇𝚽a)}]𝛿𝚽a√-𝑔 𝑑4𝑥.
∂𝐿/∂𝚽a = ∂𝐿/∂𝚽a - 𝛁𝜇[∂𝐿/∂(𝛁𝜇𝚽a)] = 0. (19.20)
19.5 Equivalent actions (등가 작용들)
∘ 기민한 독자는 EL 방정식의 (19.3)의 유도에 있어서 작용의 어떤 모호성이 있음을 인지할 것이다. 그것은 항상 전체 도함수의 어떤 지역 𝓡 위에서의
적분을 항상 경계의 표면 ∂𝓡 위로 변환할 수 있다는 사실로부터 유도한다. 우리는 그래서 Lagrangian 밀도의 다음의 수정을 고려하도록 하자.
𝓛 → 𝓛̄̄ = 𝓛 + ∂𝜇𝑄𝜇(𝚽a), (19.21)
여기서 𝑄𝜇는, 일반적으로, 그 field의 네 함수(그러나 그 도함수는 아님)일 수 있다. 그 해당하는 작용은 다음이 된다.
𝑆̄̄ = 𝑆 + ∫𝓡 ∂𝜇𝑄𝜇 𝑑4𝑥.
그 field들의𝚽a (19.9)의 변분 하에서의 작용의 변분은 다음으로 주어진다.
𝛿𝑆̄̄ = 𝛿𝑆 + ∫𝓡 ∂𝜇(𝛿𝑄𝜇) 𝑑4𝑥 = 𝛿𝑆 + ∫𝓡 ∂𝜇{(∂𝑄𝜇/∂𝚽a)𝛿𝚽a} 𝑑4𝑥.
여기서 우측의 적분 항이 경계 ∂𝓡에서 표면 적분으로 변환될 수 있다, 그 변분 𝛿𝚽a가 사라진다고 가정하면, 𝛿𝑆̄̄ = 𝛿𝑆. 여가서 𝛿𝑆̄̄ = 0 의 요구는
𝛿𝑆 = 0 와 같은 EL 방정식이 되며, 그래서 그 두 작용은 등가(equivalent) 라고 부른다.
위의 논의는 𝓛가 이차- 혹은 삼차도함수를 포함할 경우로 쉽게 연장될 수 있다. 예를 들면 이차도함수를 갖는 경우는 다음이 된다.
𝓛 → 𝓛̄̄ = 𝓛 + ∂𝜇𝑄𝜇(𝚽a, ∂𝜈𝚽a). (19.22)
∘ 앞의 수학적 묘책의 호소력있는 특징에도 불구하고, 좌표 전환을 허용하는 일반적인 바로 그 본성에 있어서는 문제에 봉착할 수도 있다. 즉,
∂𝜇𝑄𝜇 𝑑4𝑥 값이 scalar가 아니면 변형된 좌표계마다 값이 변화할 것이다. 그래서 고정된 좌표계에서만 사용하든가, 또는 가급적 진정한 공변 scalar로
만드는 것을 목표로 하여야 한다.
∘ 또한 공변미뷴을 사용하는 (19.15) 형태의 경우에는 다음의 새로운 Lagragian을 고려한다.
𝐿̄ = 𝐿 + 𝛻𝜇𝑄𝜇(𝚽a).
그러면 해당하는 작용은 다음으로 해석된다.
𝑆̄̄ = 𝑆 + ∫𝓡 𝛻𝜇𝑄𝜇√-𝑔 𝑑4𝑥. (19.23)
그리고 그 변분은 다음으로 주어진다.
𝛿𝑆̄̄ = 𝛿𝑆 + ∫𝓡 𝛻𝜇(𝛿𝑄𝜇)√-𝑔 𝑑4𝑥 = 𝛿𝑆 + ∫𝓡 𝛻𝜇{(∂𝑄𝜇/∂𝚽a)𝛿𝚽a}√-𝑔 𝑑4𝑥.
우리는 발산 정리를 사용하여 표면 적분을 얻고 여기서 𝑄𝜇가 한 vector의 성분들이어야 함에 주목한다. 이것 역시 𝛻𝜇𝑄𝜇가 하나의 스칼라장이며, 그래서
(19.23)의 우측변 두번째 항이 한 scalar 적분임을 보증한다.
[참고 사항]
... Preface (서문)에서 ...
∘ 이 책의 공변미분의 약기: 𝛁𝑏𝜐𝑎 ≡ ∂𝑏𝜐𝑎 + 𝛤𝑎𝑐𝑏𝜐𝑐 (nabla, del) ⟷ 다른 책들[Dirac의 GR (10.7) 참조]의 공변미분 표현: 𝜐𝑎;𝑏 (semicolon)
... 2. Manifolds and coordinates (다양체와 좌표)에서 ...
∘ 실제로 사람들은 'manifold(다양체)'는 일반적 수학적 의미로는 단지 'space(공간)'을 위한 한 화려한(fancy) 단어로서 간주할 수 있다.
∘ 아것은 한 다양체는 'locally(국소적으로는)' 해당하는 Euclid 공간-그것은 'smooth(매끄럽고)' 어떤 수의 차원들을 갖는다-과 같음을 의미한다.
* 'vanish'는 '0이 되다'라고 번역하기도 하지만, 여기서는 원래의 어감대로 '사라지다'로 표현함.
** 여기서는 시간 일차미분-속도 ů의 윗점 표기를 위해서, 원문의 𝑞를 u로 바꾸어 썼음.
p.s. 간략하나 심오한 Dirac's GR에 비해서 rigor는 일부 부족하지만, 나름 자상하며, 아주 훌륭한 우주론을 포함한 GR 학부용 입문서
Cambridge 대의 이론물리학자 M. P. Hobson와 두 천체물리학자 G. P. Efstathiou-저명함-와 A. N. Lasenby 공저 (2006년) GR 교과서
이 책을 발견한 것은 이책 참고문헌 중에 Dirac의 GR이 포함되어 있으며, Chapter 19에서 마찬가지로 Hamilton의 원리의 적용이 있기 때문임.
Richard Faber의 GR의 참고문헌들 가운데서 Dirac의 GR을 발견했고, 이번에는 거꾸로 그 책을 참고문헌으로 하는 이 책을 찾았음.
GR 입문서로 점차 인기가 높아지고 있어서, 일부의 저평가에도 불구하고, R. Wald의 GR 학습 전의 책으로 높게 추천한다는 글도 있었으며 ...
K.S. Thorne & R.D. Blandford Modern Classical Physics (Princeton University Press 2017)에서 우주론 추천서로 선정됨.
|
|
|





































