|
김관석
|
2018-06-29 07:54:00, 조회수 : 1,020 |
- Download #1 : fig_light_cones.jpg (71.7 KB), Download : 1

특수상대성 원리(Principles of Special Relativity)
<전제 및 용어>
특수 및 일반 상대성 이론에 관한 글은 참고문헌의 미국 대학교재 Hartle(2003)을 기본으로 하되, 참고서 Landau-Lifshitz(1939/1980)로 보완하려고 합니다.
James Hartle(1939~)도 훌륭한 학자이지만 Lev Landau(1908-1968)는 러시아의 천재 과학자로서 [E. Lifshitz(1919-1985)는 제자] 원전을 기술한 것입니다.
Hartle 책은 학부생을 위한 교과서로 출발하였으나 Landau-Lifshitz의 책은 전 10권의 역학(mechanics) 제2권으로서 대학원생을 위한 더 높은 수준입니다.
대학 수준의 '최대한의 간결성과 수학적 엄밀성(rigor)을 지향하는 짧고 정확한 상대성이론 해설'을 목표로 하여 수시 업데이트하겠습니다~
⦁ 계(frame): 여기서는 좌표 시스템(a system of coordinate)과 동의어
⦁ 기준계(reference frame): 공간(space)에서 입자(particle)의 위치와 시간을 알리는 시계(clock)를 갖는 계(frame)
⦁ 관성계(inertial frame): 외력(external force)를 받지 않고 상대적인 등속으로(uniformly) 움직이는 기준계(reference frame)
⦁ 맥스웰의 법칙과 마이컬슨-몰리(Michelson-Morley) 실험에 따라 모든 관성계에서 광속 c ≅ 2.998*1010cm/s.
⦁ 대부분의 상대성이론의 도출은 사고 실험(thought experiment)[Gedankenexperiment]에 의함.
1. 상호작용의 전파 속도(Velocity of propagation of interaction)
상대성원리(principle of relativity)란 모든 관성계(inertial frame)에서 자연의 법칙(laws of nature)의 동일성으로, 이는 실험에 의해 증명되었습니다.
그러면 계(frame)안에서 물질 입자들(material particles)의 상호작용(interaction)이 있다고 했을 때 전파 속도(velocity of progaation)는 과연 어떠할까요?
갈릴레오의 상대성 원리(principal of relativity of Galileo)에서는 무한 속도(infinite velocity)로 전파된다고 가정하였었으나, 실제의 상호 작용은 ...
아인슈타인의 상대성 원리(principal of relativity of Einstein)에 의해 광속으로 전파됨이 밝혀졌습니다!
우리는 보통 상대성이론에 의한 역학(mechanics)을 뉴톤 역학(Newtonian mechanics)과 대비해 상대론적 역학(relativisic mechanics)이라 부릅니다.
위 그림fig.1.과 같이 xyz 좌표계를 가진 K 관성계와 이와 x축 방향으로 일정한 속도로 이동하는 x'y'z' 좌표계의 K’ 관성계를 생각해 보기로 합시다.
K’ 관성계의 A 지점에서 신호(signal)가 양쪽으로 출발했다고 가정하면 모든 관성계에서 광속은 c이므로 같은 거리의 B와 C에 동시에 도달합니다.
하지만 K 관성계에 있는 관찰자(observer)에게는 B는 A를 향해서 가고 C는 A에서 멀어지므로 B에 먼저 도달하고 C에는 나중에 도달하게 보입니다.
한 관성계에서 동시인 사건이 상대적 등속으로 움직이는 다른 관성계에서는 동시인 사건이 아니므로 뉴톤의 시간 개념은 폐기해야 합니다.
예를 들자면 태양의 한 사건이 아이슈타인 상대성이론에서는 광속 거리인 약 8분 뒤에 작용하지만 갈릴레오의 상대성에서는 즉시 작용한다는 차이입니다.
하지만 관성계간 거리나 속도가 광속 c에 비교해 크지 않을 때에는 실용적 근사식인 뉴톤의 역학을 그대로 적용할 수 있는 것입니다. [Landau-Lifshitz p.3]
2. 간격(Intervals)
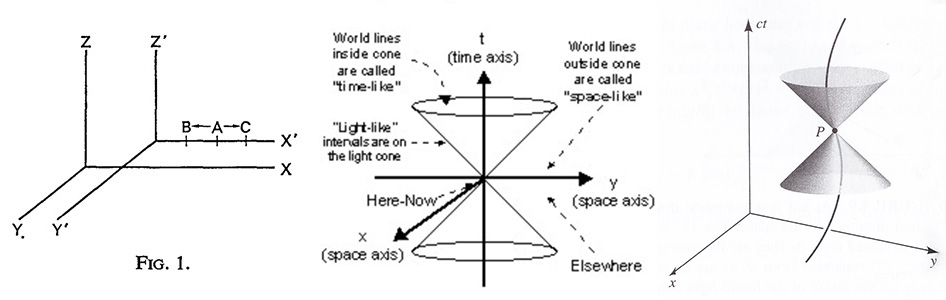
사건(event)은 발생한 시간과 장소로 기술되므로 가상의 4차원 공간을 3 공간축(three space axis)[x]와 시간축(time axis)[t]로 편의상 자주 표기헙니다.
그 시공간속에서 사건(events)들은 점으로 표기하여 세계점(world points)이라고 부르며 그 점의 움직임을 세계선(world line)이라고 부릅니다.
이제 위 그림의 K와 K’ 관성계로 광속 불변의 원리(the principle of the invariance of the velosity of light)의 적용을 수학적으로 살펴 보겠습니다.
관성계 K의 시간을 t, 관성계 K’의 시간을 t’라 하고 사건의 간격(interval)을 ∆s라고 하면 다음의 '간격 불변(invariance of intervals) 식'이 성립합니다.
시계(clock)는 L거리의 A거울(mirror)과 B거울사이를 왕복하는 빛 펄스(light pulse)의 시간 간격(time interval) : ∆t = 2L/c 을 측정함.
관성계 K에서 ∆t = 2L/c, ∆x = ∆y = ∆z = 0 일 때, x축 방향 등속 V로 이동하는 관성계 K'의 ∆t' = (2/c) *√[L² +( ∆x'/2)²], ∆x' = V∆t', ∆y' = ∆z' = 0
-(c∆t')² + (∆x')² = - 4[L² + (∆x'/2 )² ] + (∆x')² = -4L² = -(c∆t)² <- ∆x = ∆y = ∆z = 0, ∆y' = ∆z' = 0 를 양변에 더하고 정리하면,
-(c∆t)² + (∆x)² + (∆y)² + (∆z)² = -(c∆t')² + (∆x')² + (∆y')² + (∆z')² = -4L² <- 모든 관성계의 한 불변량(an invariant)을 식별하는 열쇠.
(∆s)² ≡ -(c∆t)² + (∆x)² + (∆y)² + (∆z)² <2-1a>
ds² = -c²dt² + dx² + dy² + dz² <2-1b> <- 미분 버전
3. 고유시간(Proper Time)과 시간 팽창(Time Dilation)
(∆s)² > 0 공간꼴 분리(spacelike seperated)
(∆s)² = 0 널null 분리(null seperated or lightlike seperated)
(∆s)² < 0 시간꼴 분리(timelike seperted)
ds² = -c²dt² + dx² + dy² + dz² <2-1c> <- Hartle책이 interval로 사용함. * default
ds² = c²dt² - dx² - dy² - dz² <2-1d> <- Landau-Lifshitz책이 interval로 사용함.
위 그림처럼 널null 분리된 점들이 광추[光錐-빛원뿔](light cone)가 되며 질량을 가진 물체는 광추 내부의.시간꼴(timelike) 세계선을 따라 움직입니다.
여기서 시계(clock)는 시간꼴 거리(timelike distance)를 재는 도구(device)이고, 자(ruler)는 공간꼴 거리(spacelike distance)를 재는 도구입니다.
시간성 영역안의 곡선(curve)을 따라 움직이는 거리인 τ는 실제 시간이며 고유시간(proper time)이라 지칭합니다. [Hartle p.60-63]
dτ² ≡ - ds²/c² <3-1>
광추-빛원뿔 내부의 시간성 영역안의 세계선world line 상의 두점 A와 B간 고유시간은 τAB를 위의 두 식에 의해서 계산하면...
τAB = ∫(trom A to B)dτ = ∫(trom A to B) √ {dt²-(dx²+dy²+dz²)/c²} = ∫(trom A to B) dt √ {1-(dx²+dy²+dz²)/dt²c²} = ∫(trom A to B) dt √ (1-V²/c²)
dτ = dt √ (1 - V²/c²) <3-2> <- 고유시간 팽창(proper time dilation) * '지연'(delay?)은 구/일본식 오역
정지한 관성계 K와 V로 움직이는 관성계 K'에 각각 속한 시계들clocks을 통해 dt'가 무엇을 의미하는가를 알아보기로 합시다. [Landau p.7-9]
관성계 K'에 있는 시계는 시간간격l dt 동안 √ (dx² + dy² + dz²) 거리를 이동하며 그 관성계 내에서 정지해 있으므로 dx' = dy' = dz' = 0 입니다.
ds² = -c²dt² + dx² + dy² + dz² =-c²dt'²
dt' = dt √ [1- (dx² + dy² + dz² )/c²dt²], (dx² + dy² + dz² )/dt² = V²
dt' = ds/c = dt √ (1 - V²/c²) <3-3> <- 관성계 K'에 속한 시계의 시간 팽창(time dilation)
참고문헌 Landau, L.D & Lifshitz, E.M. The Classical Theory of Fields (fourth edition, Butterworth-Heinemann 1986/1938)
Hartle, J.B. Gravity: An Introduction to Einstein’s General Relativity (Addison-Wesley 2003)
p.s. 위 Landau-Lifshitz (1962)는 Hartle (2003)의 참고문헌 중 첫번째로서 그 아래에 다음의 코멘트가 있음.
'The 150 pages of the text devoted to general relativity give a concise introduction to the basics of the subject
in the clear and straightfoward Landau and Lifshitz style, although few application are covered in any depth.'
Landau, L. D.와 Lifshitz, E.M.의 상기 책은 1939년 Russian 초판본이래 러시아 7판이 Lifshitz에 의해 출판되고,
1951년, 1962년, 1971년, 1980년 네번 영어 번역판(역자는 모두 M. Hamermesh)이 나왔음. |
|
|





































