|
김관석
|
2019-06-16 16:51:19, 조회수 : 1,004 |
- Download #1 : dff_1_2.jpg (44.3 KB), Download : 2
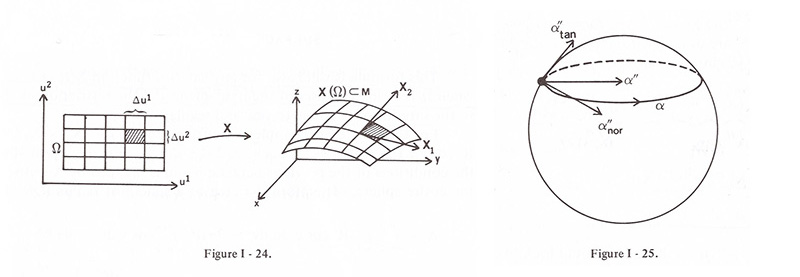

4. The First Fundamental Form <- Figure I-24 참조
∘ If 𝛂(t) = 𝐗 (u(t), v(t)), a≤ t ≤b, <- a curve on a surface; s = s(t): arc length, total length L = s(b) = ∫ba∥𝛂'(t)∥dt,
(ds/dt)2 = ∥𝛂'∥2 = 𝛂' ∙ 𝛂' = (u'𝐗1 + v'𝐗2) ∙ (u'𝐗1 + v'𝐗2) = u'2(𝐗1 ∙ 𝐗1) + 2u'v'(𝐗1 ∙ 𝐗2) + v'2(𝐗2 ∙ 𝐗2) <- by eq.(3)
𝐸 = 𝐗1 ∙ 𝐗1, 𝐹 = 𝐗1 ∙ 𝐗2, 𝐺 = 𝐗2 ∙ 𝐗2 <- following Gauss [4-4]
(ds/dt)2 = 𝐸(du/dt)2 + 2𝐹[(du/dt)(dv/dt)] + 𝐺(dv/dt)2 [4-5]
ds2 = 𝐸 du2 + 2𝐹 dudv + 𝐺 dv2 <- the first fundamental form 第一基本形式 or metric form 計量形式 [4-6]
∘ If 𝐯 = a𝐗1 + b𝐗2, 𝐰 = c𝐗1 + d𝐗2, <- (a,b,c,d는 실수) 𝐌의 한점에서의 tangent vectors
then 𝐯 ∙ 𝐰 = (a𝐗1 + b𝐗2) ∙ (c𝐗1 + d𝐗2) = 𝐸ac + 𝐹(ad + bc) + 𝐺bd.
⌈ 𝐸 𝐹 ⌉ ⌈ c ⌉
𝐯 ∙ 𝐰 = (a,b) ⌊ 𝐹 𝐺 ⌋ ⌊ d ⌋ <- matrix product 표기 방식 [4-8]
∘ 𝐔 = 𝐗1 ⨯ 𝐗2 /∥𝐗1 ⨯ 𝐗2∥ <- unit normal vector, ∵ 𝐔⊥𝐗1 and 𝐗2, ∥𝐔∥= 1, 𝐗1 ⨯ 𝐗2 ≠ 0
∥𝐗1 ⨯ 𝐗2∥2 = (𝐗1 ∙ 𝐗1) (𝐗2 ∙ 𝐗2) - (𝐗1 ∙ 𝐗2)2 = 𝐸𝐺 - 𝐹2 <- the identity of Lagrange 라그랑주 恒等式 [4-9]
∵ 𝐗1 ⨯ 𝐗2 = 𝐗1 𝐗2 sin𝜃, 𝐗1 ∙ 𝐗2 = 𝐗1 𝐗2 cos𝜃, ∣𝐗1∣2 ∣𝐗2∣2 sin2𝜃 = ∣𝐗1∣2 ∣𝐗2∣2 - ∣𝐗1∣2 ∣𝐗2∣2 cos2𝜃
∘ 𝑔𝑖𝑗 = 𝐗𝑖 ∙ 𝐗𝑗 [※ notaional change] → 𝑔11 = 𝐸, 𝑔21 = 𝐹, 𝑔22 = 𝐺
⌈ 𝑔11 𝑔12 ⌉ ⌈ 𝐸 𝐹 ⌉
⌊ 𝑔21 𝑔22 ⌋ = ⌊ 𝐹 𝐺 ⌋ <- the matrix of the geometric form
∘ 𝑔 = ∥ 𝐗1 ⨯ 𝐗2∥2 <- let 𝑔 = det (𝑔𝑖𝑗) = 𝐸𝐺 - 𝐹2 [※ notaional change] [4-10]
( the Einstein Summation Convention 아인슈타인 合 規約 을 적용하기 시작합니다 .) <- Tensor 해석 I-1 참조
∘ ds2 = 𝑔𝑖𝑗du𝑖du𝑗 [notaional change: ∑ 𝑖,𝑗 𝑔𝑖𝑗du𝑖du𝑗] <- the first fundamental form or metric form by eq.(4-6)
∘ 𝐯 ∙ 𝐰 = 𝑔𝑖𝑗v𝑖w𝑗 [notaional change: ∑ 𝑖,𝑗 𝑔𝑖𝑗v𝑖] <- by eq.(8); 𝐯⊥𝐰, if and only if * 𝐯 ∙ 𝐰 = 0. [4-11]
∘ 𝛂' = u𝑖'𝐗𝑖 [notaional change: ∑ 𝑖 u𝑖'𝐗𝑖] <- by eq.(3)
∘ 𝑔𝑖𝑗: the components of the matrix inverse of (𝑔𝑖𝑗) ↦ (𝑔𝑖𝑗)(𝑔𝑖𝑗) = 𝐈 <- 𝐈: identity matrix
𝑔𝑖𝑗𝑔𝑗𝑘 = 𝛿𝑘𝑖, 𝛿𝑘𝑖 = {(1 if 𝑖 = 𝑘), (0 if 𝑖 ≠ 𝑘)} [notaional change: ∑ 𝑖,𝑗 𝑔𝑖𝑗𝑔𝑗𝑘] [4-12]
𝑔11 = 𝑔22/𝑔, 𝑔12 = 𝑔21 = -𝑔12/𝑔, 𝑔22 = 𝑔11/𝑔 <- inverse matrix**, 𝑔 = det (𝑔𝑖𝑗); if and only if 𝑔 ≠ 0
∘ If a surface 𝐗;𝐃 → E3, a region 𝛺 ⊂ 𝐃 on which 𝐗 is one-to-one, 어떻게 𝐗(𝛺) 면적을 발견할 수 있을까요?
먼저 𝛺를 u1, u2축을 따라 각변이 𝛥u1, 𝛥u2인 작은 직사각형으로 나눈 후에 이를 𝐗(𝛺)로 mapping해 봅니다.
𝐗(𝛺)에서 𝛺에서의 작은 사각형들이 유사 평행사변형으로 되며 각변은 ∥𝐗1∥𝛥u1,∥𝐗2∥𝛥u2가 됩니다.
∴ 𝛥𝐴 ≈∥𝐗1∥∥𝐗2∥sin 𝜃 𝛥u1𝛥u2 = ∥𝐗1 ⨯ 𝐗2∥𝛥u1𝛥u2 = (√ 𝑔) 𝛥u1𝛥u2
𝐀 = ∬𝛺∥𝐗1 ⨯ 𝐗2∥du1du2 = ∬𝛺 (√ 𝑔) du1du2 <- function 𝐗 to 𝛺: one-to-one and regular [4-13]
5. The Second Fundamental Form <- Figure I-25 참조
∘ 이후로는 the Einstein Summation Convention 아인슈타인 合 規約 을 계속 적용합니다.
∘ The Gauss Formulas : a curve 𝛂(s) = 𝐗(u1(s), u2(s)) on 𝐌, s: arc length,
unit tangent vector 𝐓 = 𝛂' = u𝑖'𝐗𝑖; acceleration or curvature vector 𝐓' = 𝛂"; curvature k(s) = ∥𝐓'∥
𝛂" = 𝛂"tan + 𝛂"nor <- tangent and normal to the surface; in order to study the surface 𝐌 [5-14]
𝛂" = u𝑖"𝐗𝑖 + u𝑖'd𝐗𝑖/ds <- by product rule [5-15]
𝐗𝑖 ≡ ∂𝐗/∂u𝑖 = ( ∂x/∂u𝑖, ∂y/∂u𝑖, ∂z/∂u𝑖), 𝑖 = 1, 2
𝐗𝑖𝑗 ≡ ∂2𝐗/∂u𝑗∂u𝑖 = ∂𝐗𝑖/∂u𝑗 = ( ∂2x/∂u𝑗∂u𝑖, ∂2y/∂u𝑗∂u𝑖, ∂2z/∂u𝑗∂u𝑖), 𝑖,𝑗 = 1, 2
𝐗𝑖 = 𝐗𝑖(u1(s), u2(s)) → d𝐗𝑖/ds = (∂𝐗𝑖/∂u1) u1' + (∂𝐗𝑖/∂u2) u2' = (∂𝐗𝑖/∂u𝑗)u𝑗' = u𝑗'𝐗𝑖𝑗 <- by chain rule
𝛂" = u𝑟"𝐗𝑟 + u𝑖'u𝑗'𝐗𝑖𝑗 [5-16]
𝐗𝑖𝑗 = 𝛤𝑟𝑖𝑗𝐗𝑟 + 𝐿𝑖𝑗𝐔, 𝑖,𝑗 = 1,2 <- the Gauss Formulas ; cf) Tensor 해석 II-4 b) Christoffel 기호 [5-17]
𝛂" = 𝛂"tan + 𝛂"nor = (u𝑟" + 𝛤𝑟𝑖𝑗 u𝑖'u𝑗')𝐗𝑟 + (𝐿𝑖𝑗 u𝑖'u𝑗')𝐔 [5-18]
𝛂" = [u1" + 𝛤111(u1')2 + 2𝛤112u1'u2' + 𝛤122u2')2]𝐗1 + [u2" + 𝛤211(u1')2 + 2𝛤212u1'u2' + 𝛤222(u2')2]𝐗2
+ [𝐿11(u1')2 + 2𝐿12u1'u2' + 𝐿22(u2')2]𝐔 <- full equation by the Einstein summation convention
∘ 𝐿𝑖𝑗 u𝑖'u𝑗' <- how does it curve relative that space? extrinsic(外在的) geometry [5-19]
𝐿𝑖𝑗 = 𝐗𝑖𝑗 ∙ 𝐔, 𝑖,𝑗 = 1,2 <- the second fundamental form of the surfaces [5-20]
ex) Let 𝐗(u,v) = (u, v, f(u,v)), (u,v) ∊ D, then 𝐗1 = (1, 0, fu), 𝐗2 = (0, 1, fv).
𝐸 = 1 + fu2, 𝐹 = fuv, 𝐺 = 1 + fv2, 𝑔 = 𝐸𝐺 - 𝐹2 = 1 + fu2 + fv2, 𝐗1 ⨯ 𝐗2 = (-fu, -fv, 1), 𝐔 = (-fu, -fv)/√ 𝑔
𝐗11= (0, 0, fuu), 𝐗12= (0, 0, fuv), 𝐗11= (0, 0, fvv) → 𝐗𝑖𝑗 = (0, 0, f𝑖𝑗); ∴ 𝐿𝑖𝑗 = f𝑖𝑗 / √ 𝑔, 𝑖,𝑗 = 1, 2
∘ Definition I-3
𝐯 = v𝑖 𝐗𝑖가 𝐏에서 𝐌에 접하는 a unit vector라면, the normal curvature 法曲率 in the v direction k는,
𝑘n(𝐯) = 𝐿𝑖𝑗 v𝑖v𝑗 로 정의된다. [5-21]
∘ 𝛂가 𝐌에 있는 임의의 곡선으로 𝛂(s0) = 𝐏, 𝛂(s0)' = 𝐯이면, 𝛂(s0)'= u𝑖'(s0)𝐗𝑖(u1(s0), u2(s0)), v𝑖 = u𝑖'(s0)이 됩니다.
𝑘n(𝐯) = 𝐿𝑖𝑗 u𝑖'u𝑗' = 𝛂" ∙ 𝐔 = ∓∥𝛂"∥ <- by eq.16 에서 ur" 𝐗r ∙ 𝐔 = 0; eq. 20 [5-22]
'0'이아닌 tangent vector에 대해서 normal curvature의 개념을 다음과 같이 확장시킬 수 있습니다.
𝑘n(𝐯) = 𝐿𝑖𝑗 v𝑖v𝑗/∥𝐯∥2 = 𝐿𝑖𝑗 v𝑖v𝑗/ 𝑔mnvmvn <- by eq. 21; 우변의 v를 v/∥v∥로 교체함.
p.s. 곡면 𝐌 위에 있는 곡선 방정식의 1차 2차 미분 결과를 이용해서 곡면 자체의 curvature를 발견하는 것이 핵심임.
특히 곡면 위에서의 Christoffel symbols를 포함한 Gauss Formulas-'Tensor 해석 II-2'과 비교됨-에 주목 바람.
* 'if and only if ' 혹은 줄여서 'iff '라고도 쓰는데 동치(同値) 또는 필요충분조건을 가리킴.
** inverse matrix(逆行列) 𝐀-1 = (Ȃ𝑖𝑗)T/det 𝐀 <- cofactor(餘因子) Ȃ𝑖𝑗 = (-1)𝑖+𝑗𝑀𝑖𝑗, 𝑀𝑖𝑗: the 𝑖,𝑗 minor of 𝐀 |
|
|





































