|
김관석
|
2019-09-06 09:38:00, 조회수 : 919 |
- Download #1 : gr_3_4p.jpg (46.4 KB), Download : 1
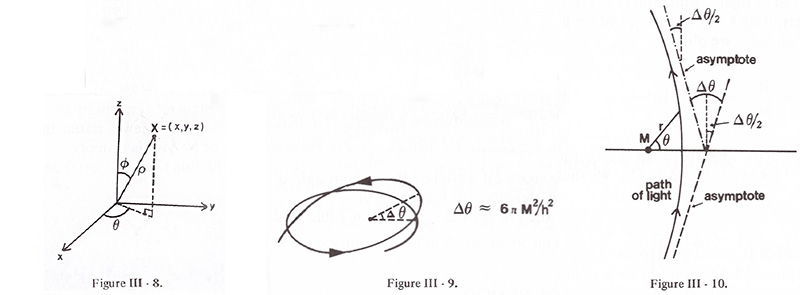

8. The Schwarzschild Soutions <- Figure III-8 참조
Karl Schwarzschild(1873-1916)는 1916년 Einstein이 일반 상대성의 발표 수개월 만에 Einstein의 방정식의 해를 구했습니다.
앞 장에서의 경우처럼 구형 대칭으로서 대전되지 않고 정적인 질량 분포를 나타내는 경우로서 'Schwarzschild 解' 라고 부릅니다.
∘ [단계 1] 먼저 proper time 을 구형 대칭에 적합한 구면 좌표계의 삼각함수 및 자연로그 상수 e의 함수로 변형합니다.
𝑅μν = 0, μ,ν = 0,1,2,3, d𝜏2 = dt2- dx2-dy2-dz2, x = 𝜌 sin 𝜙 cos 𝜃, y = 𝜌 sin 𝜙 sin 𝜃, z = 𝜌 cos 𝜙 [8-141,142,143]
d𝜏2 = dt2 - d𝜌2 - 𝜌2d𝜙2 - 𝜌2sin2 𝜙 d𝜃2 . <- This is still, of course, the metric of flat spacetime [8-144]
d𝜏2 = U(𝜌)dt2 - V(𝜌) d𝜌2 - W(𝜌)(𝜌2d𝜙2 + 𝜌2sin2 𝜙 d𝜃2) <- U, V, W are function of 𝜌 differ slightly from unity [8-145]
d𝜏2 = A(r)dt2 - B(r) dr2 - r2d𝜙2 - r2sin2 𝜙 d𝜃2) <- If we introduce the variable r = 𝜌 W(𝜌)1/2 [8-146]
d𝜏2 = e2mdt2 - e2n dr2 - r2d𝜙2 - r2sin2 𝜙 d𝜃2) <- finally, define m = m(r), n = n(r) by e2m = A and e2n = B [8-147]
d𝜏2 = 𝑔μνdxμ dxν, x0 = t, x1 = r, x2 = 𝜙, x3 = 𝜃
⌈ e2m 0 0 0 ⌉
(𝑔μν) = ┃ 0 - e2n 0 0 ┃ and determinant 𝑔 = - e2m+2n r4 sin2 𝜙 [8-148]
┃ 0 0 - r2 0 ┃
⌊ 0 0 0 - r2sin2 𝜙 ⌋
∘ [단계 2] 일반 상대성 metric 계수가 포함된 Christoffel 기호를 산출한 후, Einstein 방정식의 Ricci tensor 𝑅μν = 0 해를 구합니다.
Since our coordinate system is orthogonal, 𝑔μν = 0 for μ ≠ ν, 𝑔μν = 0 for μ ≠ ν, 𝑔μμ = 1/𝑔μμ for all μ, in Eq. (126) then reduced to
𝛤𝜆μν = (1/2)𝑔𝜆𝜆(∂ 𝑔μ𝜆/∂xν + ∂ 𝑔μ𝜆/∂xμ - ∂ 𝑔μν/∂x𝜆) (no sum) [8-149]
Case 1: For 𝜆 = ν, 𝛤𝜆μν = (1/2)(∂ /∂xμ) ln┃𝑔μν┃ (no sum) [8-150]
Case 2: For μ = ν ≠ 𝜆, 𝛤𝜆μμ = -(1/2𝑔𝜆𝜆) ∂ 𝑔μμ/∂x𝜆 (no sum) [8-151]
Case 3: For μ, ν, 𝜆 all distinct, 𝛤𝜆μν = 0 [8-152]
𝛤010 = 𝛤001 = m' 𝛤100 = m'e2m-2n 𝛤111 = n' 𝛤122 = -re-2n 𝛤212 = 𝛤221 = 1/r
𝛤133 = -re-2nsin2𝜙 𝛤313 = 𝛤331 = 1/r 𝛤323 = 𝛤332 = cot 𝜙 𝛤233 = - sin 𝜙 cos 𝜙 [8-153]
ln┃𝑔┃1/2 = (1/2) ln (- e2m+2n r4 sin2 𝜙) = m + n + 2 ln r + ln sin 𝜙
𝑅μν = (∂2/∂ xμ∂ xν) ln┃𝑔┃1/2 - ∂𝛤𝜆μν /∂x𝜆 + 𝛤βμ𝜆 𝛤𝜆νβ - 𝛤βμν (∂ /∂xβ) ln┃𝑔┃1/2 [8-154]
𝑅00/e2m-2n = -m" + m'n' - m'2 - 2m'/r = 0 𝑅11 = m" - m'n' + m'2 - 2n'/r = 0 [8-155a,155b]
𝑅22 = e-2n(1 + rm' - rn') - 1 = 0 𝑅33 = 𝑅22 sin2 𝜙 = 0 [8-155c,155d]
∘ [단계 3] 𝑅μν = 0 로부터 m과 n의 관계식을 구하고, 𝑔00 = 1 + 2𝚽 = 1 - 2M/r 로부터 m과 n을 소거한 최종해를 구합니다.
Now adding Eq. (153a) and (153b), m' + n' = 0 and m + n = b [b: constant]. As r → ∞, b → 0. Consequently, m = - n.
From eq. (155c) 1 = (1 + 2rm')e2m = (re2m)', Hence re2m = r + C, 𝑔00 = e2m = 1 + C/r. From eq. (135)(121) 𝑔00 = 1 - 2M/r.
Finally we arrive at the solution! d𝜏2 = (1 - 2M/r) dt2 - (1 - 2M/r)-1 dr2 - r2d𝜙2 - r2sin2 𝜙 d𝜃2 ▮ [8-156]
9. Orbits in General Relativity <- Figure III-9 참조
Newton의 만유인력의 법칙을 통한 행성의 궤도식를 갖고서, 일반 상대성의 가정에 따라서 같은 양상으로 기술하기로 합니다.
우리는 궤도 방정식 (116)과 놀랍게 가까운 예측을 보게 되며, 천문 관측 결과가 압도적으로 Einstein을 지지함을 알게 됩니다.
∘ [단계 1] Schwarzschild 해와 timelike geodesic 방정식을 통해서 Newton적 궤도 방정식 (114)에 상대론적 항이 추가된 해을 구합니다.
d𝜏2 = (1 - 2M/r) dt2 - (1 - 2M/r)-1 dr2 - r2d𝜙2 - r2sin2 𝜙 d𝜃2 [9-157]
d2x𝜆/d𝜏2 + 𝛤𝜆μν (dxμ/d𝜏) (dxν/d𝜏) = 0, 𝜆 = 0,1,2,3 <- x0 = t, x1 = r, x2 = 𝜙, x3 = 𝜃 [9-158]
Christoffel symbols are obtained from Eq. (153), where prime defferntiation with respect to r, n = -m이며, and e2m = 1 - 2M/r
If 𝜆 = 0, d2t/d𝜏2 + 2m' (dr/d𝜏) (dt/dr) = 0, If 𝜆 = 1, d2r/d𝜏2 + m'e2m-2n(dt/d𝜏)2 + n'(dr/d𝜏)2 - re-2m(d𝜃/d𝜏) = 0 [9-159a,159b]
If 𝜆 = 2, d2𝜙/d𝜏2 + 2/r (dr/d𝜏) (d𝜙/dr) - sin 𝜙 cos 𝜙 (d𝜙/d𝜏)2 = 0, If 𝜆 = 3, d2𝜃/d𝜏2 + 2/r (dr/d𝜏) (d𝜙/dr) = 0 [9-159c]
For convenience later, let 𝛾 = 1 - 2M/r = e2m. From Eq. (159a), we may rewrite (d/d𝜏){ln (dt/d𝜏)} = -2 dm/dr
which can be intergrated and then exponetiated to give dt/d𝜏 = be-2m= b/ 𝛾, b: positive constant [9-160]
Eq. (159c) can be intergrated to obtain (as was Eq. (41b)) to obtain r2 d𝜃/d𝜏 = h, h: positive constant [9-161]
From Eq. (157) with 𝜙 = 𝜋/2, 1 = 𝛾 (dt/d𝜏)2 - 𝛾-1(dr/d𝜏)2 - r2(d𝜃/d𝜏)2 = 𝛾 (b/𝛾)2 - 𝛾-1{(dr/d𝜃)(h/r2)}2 - r2(h/r2)2 [9-162]
Applying 𝛾 = 1 - 2M/r, u = 1/r and du/d𝜃 = -(1/r2)dr/d𝜃 and differentiating with d𝜃 d2/d𝜃2 + u = M/h2 + 3Mu2 [9-163]
∘ [단계 2] 앞에서 구한 일반 상대론적 궤도 방정식에서 나타난 근일점 이동 항으로부터 근사해 방정식을 유도합니다.
For the first approximation of 3Mu2, we may give u1 = u(𝜃), u1 = (M/h2)(1 + e cos 𝜃) [9-164]
d2/d𝜃2 + u = M/h2 + 3M(1 + 2e cos 𝜃 + e2 cos2 𝜃) and because cos2 𝜃 = (1 + cos 2𝜃)/2
d2/d𝜃2 + u = M/h2 + 3M3/h4 + 3M3e2/2h4 + (6M3e/h4) cos 𝜃 + (3M3e2/2h4) cos 2𝜃 [9-165]
Lemma III-5
Let A be a real number, u = A is a solution of d2/d𝜃2 + u = A, u = (1/2) 𝜃 sin 𝜃 is a solution of d2/d𝜃2 + u = A cos 𝜃
u = -(A/3) cos 2𝜃 is a solution of d2/d𝜃2 + u = A cos 2𝜃
Applying the Lemma III-5 to each of the four tems of Eq. (165) and adding e cos 𝜃 which is a soultion of d2/d𝜃2 + u = 0,
u = (M/h2)[1 + 3M2/h2(1 + e2/2) + e cos 𝜃 + (3M2e/h2) 𝜃 sin 𝜃 - (M2e2/2h2) cos 2𝜃], e: constant [9-166]
Since 3M2/h2(1 + e2/2) is quite small (e.g. 8 ⨯ 10-8 for Mercury and final term with cos 2𝜃 is very small, both are negligible,
u ≈ (M/h2)[1 + e cos 𝜃 + (3M2e/h2) 𝜃 sin 𝜃], using approximation cos (3M2e/h2) ≈ 1, sin (3M2e/h2) ≈ (3M2e/h2)
u ≈ (M/h2)[1 + e cos (𝜃 - (3M2e/h2) 𝜃)] <- ∵ cos (𝜃 - 𝑀) = cos 𝜃 cos 𝑀 + sin 𝜃 sin 𝑀, 𝑀: 3M2e/h2 [9-167]
u has maximum value when 𝜃 = 0 and 𝜃 - (3M2e/h2) 𝜃 = 2𝜋, therefore 𝜃 = 2𝜋/ (1 - 3M2/h2) ≈ 2𝜋(1 + 3M2/h2)
[since for small x, (1 - x)-1 ≈ 1 + x] The direction of perihelion advances 𝛥𝜃 ≈ 6𝜋M2/h2, h2/M = ed = a(1 - e2), by Eq. (119),
The amount of procession per century 𝛥𝜃cent = n𝛥𝜃 = 6𝜋M2/h2n = 6𝜋M2n/a(1 - e2), n = the number of orbits per century ▮
∘ [단계 3] 최종의 방정식으로부터 산출된 근사해가 천문학에서 관측된 결과와 얼마만큼 차이를 보이는지를 체크해 봅니다.
Planet a(∻1011cm) e n General Relativity Observed
Mercury 57.91 0.2056 415 43.03 43.11 ± 0.45
Venus 108.21 0.0068 149 8.6 8.4 ± 4.8
Earth 149.60 0.0167 100 3.8 5.0 ± 1.2
Icarus 161.0 0.827 89 10.3 9.8 ± 0.8
수성, 금성, 지구와 소행성 이카루스를 위한 데이터들은 전반적으로 그 결과가 강력하게 Einstein의 이론의 예측과 일치합니다.
10. The Bending of Light <- Figure III-10 참조
∘ [단계 1] 빛은 lightlike geodesic을 따라 움직이는 proper time = 0 에 해당하는 태양의 질량과 반지름의 함수로 휘어지는 각도를 구합니다.
d2x𝜆/d𝜌2 + 𝛤𝜆μν (dxμ/d𝜌) (dxν/d𝜌) = 0, 𝜆 = 0,1,2,3 <- d𝜏/d𝜌 = 0, 𝜙 = 𝜋/2
d2/d𝜃2 + u = 3Mu2 u: 1/r <- the left side of Eq. (162) is zero, since d𝜏/d𝜌 = 0 replaces d𝜏/d𝜏 = 1. 'Classnotes' in detail [10-168]
u = 1/r = (1/ R) cos 𝜃 R: the minimumdistance from the Mass to the path of light ray, when M = 0 or x = r cos 𝜃 = R [10-169]
For a light ray grazing the sun, R⊙ ≈ 6.96 ⨯ 1010 cm, M⊙ ≈ 1.48 ⨯ 105 cm. Therefore u ≈ (1/ R) cos 𝜃, substitute it for Eq. (168).
d2/d𝜃2 + u ≈ (3M/R2) cos2 𝜃 = (3M/2R2) (1 + cos 2𝜃). By Lemma III-5, u1 = (3M/2R2){1 - (1/3) cos 2𝜃} = (M/R2){2 - cos2 𝜃)
u = 1/r = (1/ R) cos 𝜃 + (M/R2){2 - cos2 𝜃) [10-170]
From Figur III-10, as r → ∞, 𝜃 will approach ∓ (𝜋/2 + 𝛥𝜃/2). Since 𝛥𝜃 is vey small the cos2 𝜃 term in Eq. (170) is negligible.
Passing to the limit of Eq. (170) as r → ∞, 0 = (1/ R) cos 𝜃 (𝜋/2 + 𝛥𝜃/2) + 2M/R2,
Consequently, 2M/R = - cos (𝜋/2 + 𝛥𝜃/2) = sin 𝛥𝜃/2 ≈ 𝛥𝜃/2 or 𝛥𝜃 ≈ 4M/R. For the sun, 𝛥𝜃 ≈ 8.51 ⨯ 10-6 radians ≈ 1.75". ▮
∘ [단계 2] 다음은 Newton 역학으로 빛의 진행을 e > 1 인 쌍곡선 함수의 경로에서 태양의 질량과 반지름의 함수로 휘어지는 각도를 구합니다..
The path of a photon is on brach of a hyperbola Eq. (116) with e > 1, 1/r = (M/r2)(1 + e cos 𝜃) where h = r2 d𝜃/dt [10-171,172]
Consider a case of a ray grazing the sun at the nearest position, r = R⊙, 𝜃 = 0, from Eq. (107) we get r d𝜃/dt = 1(speed of light)
and h = r. Then Eq. (172) gives h = R⊙. Now we obtain from Eq. (171) with cos 𝜃 = 1, e = R⊙/M⊙ -1 ≈ R⊙/M⊙ = 4.7 ⨯ 105
Let 𝛥𝜃N be the acute angle between the light's path asymtotes. As r → ∞ in Eq. (171), 𝜃 → ∓(𝜋/2 + 𝛥𝜃N),
0 = (M/R2) [1 + e cos (𝜋/2 + 𝛥𝜃N/2)] or 1/e = - cos (𝜋/2 + 𝛥𝜃N/2) = sin 𝛥𝜃N/2 ≈ 𝛥𝜃N/2
Hence the Newtonian deflection is 𝛥𝜃N ≈ 2/e = 2M⊙/R⊙ which is exactly half that of general relativity. ▮
∘ [단계 3] 태양 옆에서의 빛의 휘어짐에 대한 일반 상대성의 예측 값과 Newton 역학에서의 예측 값을 관측 결과와 비교합니다.
1919년 이후 몇번의 일식 때 별의 겉보기 위치 관찰과 근래의 전파에 의한 관측 결과는 압도적으로 Einstein의 이론과 일치합니다!
p.s. 뒤늦게 시작했지만 지인과 'Classnotes' 덕택에 R. Faber의 '미분기하학과 상대성 입문'을 마쳐서 너무나 기쁩니다!
GR 입문서로 이름난 Schutz나 Hartle의 책들은 수학적 엄밀성(rigor)이 결여되어 강사 없이는 학습하기 어렵다고 생각되어
그래서 수학적 엄밀성을 갖추고 있는 'GR 입문'을 찾아 헤메다가, Richard Faber 책을 발견한 것은 저에게는 크나큰 행운이었음.
이 'GR 입문'의 장점은 상대성 원리(SR/GR)의 내용 자체를 충분한 수학적 rigor를 갖고서 아주 잘 설명해주고 있다는 것임.
그 한계는 원전에 있는 공변벡터와 반변벡터 등의 tensor 해석 과정이 없이 논리을 전개하여 추가의 학습이 필요하다는 것이며,
핵심부인 energy momentum tensor 해설이 없는 등의 몇몇 단점에도 불구하고, GR 최고 입문서로 강력히 추천함! |
|
|





































