|
김관석
|
2018-07-02 00:19:56, 조회수 : 561 |
- Download #1 : lorentz.jpg (73.2 KB), Download : 3

4.1 로렌츠 변환(Lorentz Transformation)
관성계 K(K system)와 관성계 K'(K' system)사이를 연결하는 변환법칙은 ds² = -c²dt² + dx² + dy² + dz² = -c²dt'² + dx'² + dy'² + dz'² 입니다.
관성계간에 이 시공간 4차원의 비유클리드적non-Euclidiean 선요소인 이 ds를 보존하는 변환(transformation)의 중요한 예가 로렌츠 부스트(Lorentz Boosts)입니다.
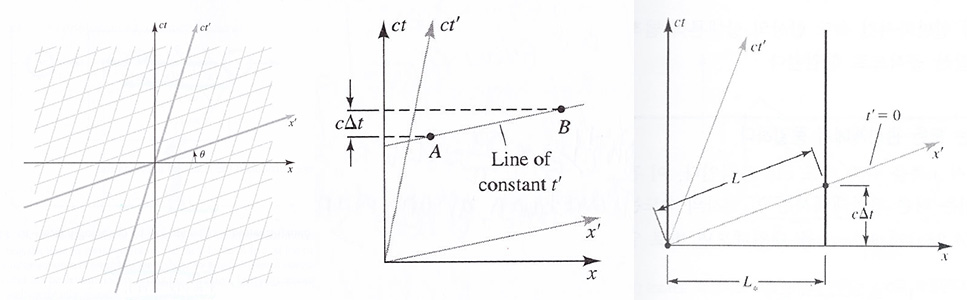
위 첫번째 그림은 시공간 다이아그램에서 좌변의 변화로서의 로렌츠 부스트로서 이는 (ct,x) 평면에서의 회전상사(analogs of rotations)를 살펴보기로 합시다.
그래서 이 관계는 시공간의 비유클리드적인 성격으로 인해 쌍곡선함수(hyperbolic functions)의 관계로 나타나게 되는 것입니다. 즉,
ct' = (coshθ)(ct) - (sinhθ)x <4-1a> <- θ(Theta 세타) 소문자
x' = (-sinhθ)(ct) + (coshθ)x <4-1b>
y' = y, z' = z <4-1c> <- 평면에서 기하학적으로 나타내기 위해서 y와 z는 변하지 않는 경우를 고려함.
* 쌍곡선함수는 2차원 평면상에서 매개변수 θ를 사용한 자취로 (coshθ, sinhθ)은 쌍곡선 x² - y² = 1 을 그리며 cosh²θ - sinh²θ= 1 임.
(ds)² = -(cdt')² + (dx')² + (dy')² + (dz')²
= -[coshθ(cdt) - sinhθ(dx)]² +[-sinhθ(cdt) + coshθ(dx)]² + (dy)² + (dz)²
= -(cdt)² + (dx)² + (dy)² + (dz)²
V = c(tanhθ) <4-2a> : 관성계 K'의 속도 <- x'=0 일 때 <2-1b>에서 0 = (-sinhθ)(ct) + (coshθ)x, tanhθ = sinhθ/ coshθ, V = x/t
tanhθ = V/c <4-2b> <- sinhθ = V/c /√ (1-V²/c²), coshθ = 1 /√ (1-V²/c²)
γ = 1/√ (1-V²/c²) <4-3> <- γ(Gamma 감마) 소문자, coshθ 값, 표기 간소화를 뤼해 도입됨.
t' = γ (t - Vx/c²) <4-4a>
x' = γ (x - Vt) <4-4b>
y' = y, z' = z <4-4c>
t = γ (t' + Vx'/c²) <4-5a>
x= γ (x' + Vt') <4-5b>
y= y', z = z' <4-5c>
V/c ≪ 1 (V가 광속보다 아주 작을 때): x = x' + Vt, y = y', z = z', t = t' + (V/c²)x' <4-6> <- 근사식
위 두번째 그림은 예로서 관성계 K'에서 동시인 사건들(events) A와 B가, K syetem에서는 A사건 이후에 B가 일어난다는 것을 보여주고 있습니다.
∆t = γ (V/c²)∆x' <4-7> <- ∆t' = 0, ∆x' = x'B - x'A , <4-5a> : 동시성의 상대성(the relativity of simultaneity) [Hartle p.73]
위 세번째 그림은 길이의 로렌츠 수축(Lorentz Contraction)을 보여 주는 것으로 K system에서 L₀ 인 막대rod가 K' system에서는 어떻게 될까하는 것입니다.
K system에서 L₀ 떨어진 점이 K' system에서 t' = 0, x'축에 있으면서 c∆t만큼 이동한 거리 L인데 길게 보이나 비유클리드 기하이라서 실제로는 더 짧습니다.
L = L₀ √ (1-V²/c²) <4-8> <- <4-5b>, ∆x = L₀ = γ ∆x', ∆x' = L = 1/γ ∆x = 1/γ L₀ : 로렌츠 수축(Lorentz Contraction) [Hartel p.70]
∆t' = ∆t √ (1-V²/c²) <4-9> <- <4-5a>, ∆t = t₂- t₁를 대입하여 정리해 보면 <3-3>과 일치함! 시간 팽창(time dilation) [Landau-lifshitz p.12]
4.2 속도의 변환(Transformation of Velocities)
이번에는 K system에서 x축을 따라 속도 V로 움직이는 K' system에서는 물질 입자의 속도가 어떻게 보이는 가하는 속도 변환 공식을 살펴보기로 합니다.
K system에서 입자 속도의 각 x, y, z 성분을 각 𝑉x, 𝑉y, 𝑉z라 하고 K' system에서의 입자속도를 각 𝑉x', 𝑉y', 𝑉z'라 하면 <4-5a, 5b, 5c>에서,
dt = γ (dt' + V dx'/c²), dx= γ (dx' + V dt'), dy= dy', dz = dz', γ = 1/√ (1 - V²/c²), dt/dx = 𝑉x 이므로
𝑉x =[𝑉x' + V]/[1 + 𝑉x'* V/c²] <4-10a>
𝑉y = 𝑉y' √ (1 - V²/c²) /[1 + 𝑉x'* V/c²] <4-10b>
𝑉z = 𝑉z' √ ( 1- V²/c²) /[1 + 𝑉x'* V/c²] <4-10c>
𝑉x' =[𝑉x - V]/[1 - 𝑉x* V/c²] <4-11a>
𝑉y' = 𝑉y √ (1 - V²/c²) /[1 - 𝑉x* V/c²] <4-11b>
𝑉z' = 𝑉z √ (1 - V²/c²) /[1 - 𝑉x* V/c²] <4-11c>
예로서 만일 K system에서 한 입자가 x축을 따라서 광속 c로 움직인다면 상대속도 V로 움직이는 k' system에서는 어떻게 보일까 생각해 보기로 합시다.
<5-2a>에 𝑉x = c 를 대입해보면 바로 알 수 있는바 𝑉x' = (c - V) / (1 - c* V/c²) = c. 따라서, 광속은 모든 관성계에서 동일한 것입니다!
참고문헌 Landau, L.D.; Lifshitz, E.M. (1980)[1939] The Classical Theory of Fields (4th ed.) Butterworth-Heinemann
Hartle, J.B. (2003) Gravity: An Introduction to Einstein’s General Relativity, Addison-Wesley
p.s. 로렌츠 변환의 더 상세한 과정이 필요하면 이의 원전인 Landau-Lifshitz책 The Lorentzy transformation pp.9-12 을 참조 바람.
Landau-Lifshitz책은 Hartle과 달리 시간꼴 간격(timelike interval)인 ds² = c²dt² - dx² - dy² - dz² 를 사용하는 차이가 있음.
|
|
|





































