|
김관석
|
2020-06-07 01:05:07, 조회수 : 1,364 |
- Download #1 : F1_1_5p.jpg (55.8 KB), Download : 4

1. Some basic concepts and an overview of cosmology*
Cosmology is the study of the large-scale structure and behaviour of the universe taken as a whole. From the cosmological studies in the last few decades the universe is thought as not a random collection of irregularly distributed matter, but a single entity, all parts of which are in unison with all other parts. This view is the standard models. We may have to modify them when considering the inflationary models later.
Galaxies, which are congregations of about 1011 stars, are the basic constituents for the large-scale structure of the universe. They tends to occur in groups called clusters, each clusters containing from a few to a few thousand galaxies. There are some clusters of clusters, but not much evidence of clusters of clusters of clusters or higher hierarchies. So Superclusters and voids (empty region) have received much attention. Observations indicates that galaxies are spread uniformly throughout the universe at any given time on the average. This proviso at any given time is important because the universe is in a dynamic state and so the number of galaxies in any given volume changes with time. The distribution of them also appears to be isotropic about us, that is, it is the same, on the average, in all directions from us. If the distribution of galaxies is isotropic about every galaxy, then it is necessarily true that galaxies are spread uniformly throughout the universe.
We adopt here a working definition of the universe as the totality of galaxies causally connected to the galaxies that we observe. We assume that observers in the furthest-known galaxies would see distribution of galaxies around them similar to ours.
Edwin Hubble around 1930 discovered that the distant galaxies are moving away from us. The velocity of recession follows Hubble's law, according to which the velocity is proportional to distance. The rule is approximate and it does not hold for galaxies which are very near nor for those are very far. In addition to the systematic motion of recession every galaxy has a component of random motion. For nearby galaxies this random motion may be comparable to the systematic motion. The very distant galaxies also show departures from Hubble's law partly because light from them was emitted billions of years ago and the systematic motion of them in those epochs may have been significantly different from that of the present epoch.
Hubble discovered the velocity of recession of distant of galaxies by studying their red-shift. It seems unlikely that the red-shift of distant galaxies is gravitational in origin; for one this is rather large for them to be gravitational and, secondly, it increases systematically with faintness. Thus the present consensus is that the red-shift is due to velocity of recession, but an alternative explanation of a part of them on the basis of either gravitation or some hitherto unknown physical process may be discovered in future.
According to Cosmological Principle, the universe is homogeneous everywhere and isotropic about every point in it. This is really an extrapolation from observation.. It is remarkable the the universe seems to obey it. The principle asserts the universe is a single entity.
Consider any two galaxies 𝐴 and 𝐵 which are taking part in the general notion of expansion of the universe. The distance between them can be written as 𝑓𝐴𝐵𝑅, where the constant 𝑓𝐴𝐵, which depends on the galaxies 𝐴 and 𝐵, is independent of time and R is a function of time. One of the major current problems of cosmology is to determine the exact form of R(𝑡), which is called the scale factor or the radius of the universe. In some models the universe has finite spatial extent, in which case 𝑅 is related to the maximum distance between two points in the universe.
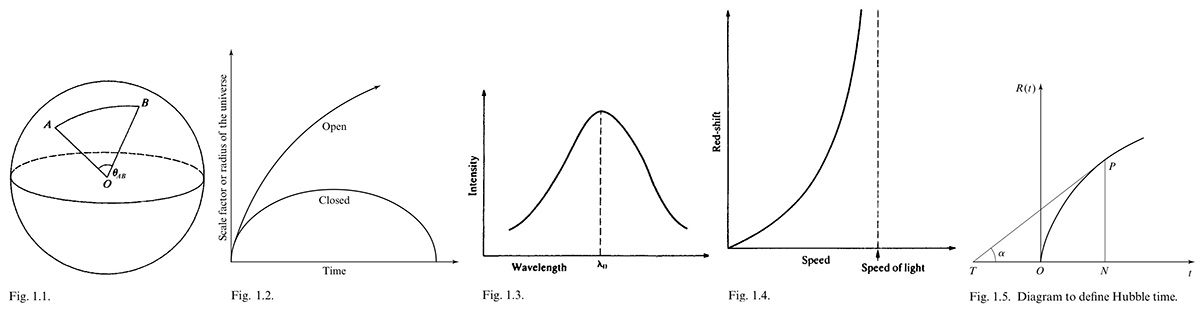
Imagine a spherical balloon like Fig.1.1, which shows the diagram of Equation (1.1), is expanding and which is uniformly covered on its surface with dots. The dot s can be considered.to correspond to galaxies ins two-dimensional universe. Let the radius of the balloon at time 𝑡 be denoted by 𝑅'(𝑡). Consider the two dots 𝐴 and 𝐵 which subtend an angle 𝜃𝐴𝐵 at the center and the distance d𝐴𝐵 between two dots on a great circle is given by
(1.1) 𝑑𝐴𝐵 = 𝜃𝐴𝐵𝑅'(𝑡).
The speed 𝑣𝐴𝐵 which 𝐴 and 𝐵 are moving relative to each other is given by
(1.2) 𝑣𝐴𝐵 = ḋ𝐴𝐵 = 𝜃𝐴𝐵Ṙ' = 𝑑𝐴𝐵(Ṙ'/𝑅'), Ṙ' ≡ 𝑑𝑅'/𝑑𝑡, etc.
Because the expansion of balloon is uniform and the angle 𝜃𝐴𝐵 remain the same for all 𝑡. We thus have a close analogy between the model of an expanding universe and the expansion of a uniformly dotted spherical balloon.
From the rate at which galaxies are receiving from each other, it can be deduced that all galaxies must have been very close each other at the same time in the past. For the universe it is believed that at the initial moment (some time between 10 and 20 billion years ago) there was a universal explosion, at every point of the universe. This was the Big Bang. Though an infinite universe remains infinite in spatial extent all time down to the initial moment, in the case of finite universe, the matter becomes more and more dense and hot in the initial moment, which is a space-time singularity. The universe is expanding now because of the initial explosion. The recession is slowing down because of the gravitational attraction of different parts of the universe to each other in the simpler models, but it not necessarily true in models with a cosmological constant.
The expansion of the universe may continue forever, as in the open models, or it may halt at some future time and contraction set in, as in closed models. These possibilities are illustrated in Fig.1.2, which shows the evolution of the scale factor or radius with in the open and close models of the universe.
There is an important a piece of evidence apart from the recession of the galaxies that the contents of the universe in the past must have been in the highly compressed form. This is the cosmic background radiation, which was discovered by Penzias and Wilson in 1965 and confirm by many observations later. The existence of this radiation can be explained as follows. When we trace the history of the universe backwards to the states of one great continuous mass, of which the temperature was very high and there have been present a great deal of electromagnetic radiation, which at some stage was in equilibrium with the matter. The spectrum of the radiation would thus correspond to a black body of high temperature. There should be the remnant of radiation and Penzias and Wilson and others discovered the cosmic background radiation having a black-body spectrum Fig.1.3, where wavelength 𝜆0 is just under 0.1 cm) with a temperature about 2.7 K.
Hubble's law implies arbitrarily large velocities of the galaxies as the distance increases indefinitely. The red-shift 𝑧 is defined as 𝑧 = (𝜆𝑟 - 𝜆𝑖)/𝜆𝑟, where 𝜆𝑖 is the original wavelength of the radiation given off by the galaxy and 𝜆r is received one by us. As the its velocity approach that of light, 𝑧 tends towards the infinity (Fig.1.4), so it is not possible to observe higher velocities than that of light. The distance at which the red-shift of a galaxy becomes infinite is called horizon. Beyond the horizon it is the space which is expanding faster than the speed of light.
There is a certain critical density, and if the present average density is above the critical one, the recession will be halt eventually. If the density is below the critical density, the attractive force is insufficient and the expansion will continue forever. The critical density at any time is given by
(1.3) 𝛆c = 3𝐻2/8π𝐺, 𝐻 = Ṙ/𝑅
Here 𝐺 is Newton's gravitational constant and R is the scale factor and represents the size of the universe in a sense. If 𝑡0 denotes the present time, then the present value of 𝐻, denoted by 𝐻0, is called Hubble's constant. For galaxies which are not too near nor too far, the velocity 𝑣 is related to the distance d by Hubble's constant:
(1.4) 𝑣 = 𝐻0𝑑.
Thus the present critical density is 3𝐻02/8π𝐺, and there are some uncertainty between 50 km/s and 100 km/s per million parsec. That is, a galaxy which is 100 million parsecs distant has a velocity away from us of 5,000-10,000 km/s. For a Hubble constant given by 50 km/s per million parsecs, the critical density equals about 5×10-30 g cm-3, or about three hydrogen atoms per thousand liters of space.
There are several other ways of determining if the universe will expanding forever. One is to measure the rate by the deceleration parameter, which is half the ratio of the actual density to the critical density. This ratio is usually denoted by 𝛺. Thus if 𝛺 < 1, the density is subcritical and the universe will expand forever, the opposite being the case if 𝛺 > 1. The present observed value of 𝛺 is somewhere between 0.1 and 2 (the lower limit could be less). In the simpler models the deceleration parameter 𝑞0, which is 1/2𝛺, is used.
Another way is to determine the precise age of the universe and compare it the Hubble time. In Fig.1.5 if 𝑂𝑁 denotes the present time (𝑡0), then 𝑃𝑁 is 𝑅 (𝑡0).
(1.5) tan 𝛼 = 𝑃𝑁/𝑁𝑇 = Ṙ(𝑡0).
(1.6) 𝑁𝑇 = 𝑃𝑁/Ṙ(𝑡0) = 𝑅(𝑡0)/Ṙ(𝑡0) = 𝐻0-1.
Thus 𝑁𝑇, the Hubble time is the reciprocal of Hubble's constant. For the value of 50 km/s per million parsecs of Hubble's Constant, the Hubble time is about 20 billion years. Again in the simple models, if the universe is older than two-thirds of Hubble time it will expand forever, and otherwise, the opposite being the case.
Whether the universe will expand forever is one of the most important unresolved problems in cosmology, both theoretically and obervationallly.
Here we shall use the term open to mean a model expanding forever, and closed for the opposite. Sometimes the expression closed is used to mean a universe with a finite volume, but a universe may expand forever at the same time like in the Friedmann models.
The standard big-bang model of the universe has three major success. Firstly, it predicts that something like Hubble's law of expansion must hold for the universe. Secondly, it predicts the existence of the microwave background (CMB) radiation . Thirdly, it predicts successfully the formation of light atomic nuclei from protons and neutrons a few minutes after the big bang. The predictions gives the correct abundance ratio for 3𝐻𝑒, 𝐷, 4𝐻𝑒 and 7𝐿𝑖. But there are some problems and puzzles in the standard model as follows.
Horizon problem: Why the universe displays a remarkable degree of large-scale homogeneity? This is most evident in the CMB radiation which is known to be uniform in temperature to about part in 1000. The uniformity is a puzzle, because, soon after the big bang, regions which were well separated could not have communicated with each other or known each other's existence. The fact that CMB radiation received from all directions is uniform implies that there is uniformity in regions whose separation must have been many times the distance 𝑐𝑡 (the horizon distance a second or so after the big bang. How did these different regions manages to have the same density, etc? If one simply assumes that the uniformity persists up to time 𝑡 = 0, there is no problem, but this this requires a very special set of special condition. This is known as the horizon problem.
Smoothness problem: A certain amount of inhomogeneity must have existed in the primordial matter to account for the clumping of the matter into galaxies and clusters of galaxies, etc. Any small inhomogeneity in the primordial matter rapidly grows into a large one with gravitational self-interaction. Thus one has to assume a considerable smootheness in the primordial matter to account for the inhomogeneity in the scale of galaxies at the present time. The problem becomes acutes if one extrapolates to 10-45s after the big bang, when one has to assume an unusual situation of of almost perfect smoothness but not quite absolute smoothness in the initial state of matter. This is known as the smoothness problem.
Flatness problem: The present big-bang model has the present observed density of matter, which we have denoted by the parameter 𝛺. If 𝛺 were initially equal to unity (this corresponds to a flat universe) it would stay equal to unity forever. On the other hand, if 𝛺 is different from unity, its departure from unity would increase with time.The present value of 𝛺 lies somewhere between 0.1 and 2. For this to be the case 𝛺 would have had to be equal to 1 to one part 1015 a second or so after the big bang, which seems an unlikely situation. This is called the flatness problem.
To deal with these problems Alan Guth in 1981 proposed the inflationary model, which differ from the standard model from about 10-45 to 10-30 seconds when it has a period of extraordinary expansion, or inflation, during which time typical distance (the scale factor) increase by a factor of about 1050 more than the standard model. Although the inflationary models solve some problems of the standard models, they throw up problems of their own problems. These models will be considered in detail.
The period referred to as the very early universe provides a testing ground for various theories of elementary particles. as one extrapolates toward the big bang at 𝑡 = 0, densities become higher and higher and the curvature of space-time becomes correspondingly higher, and general relativity becomes untenable and one has to resort to the quantum theory of gravitation. Some progress has been made in the quantum cosmology, in which quantum consideration throw some light on problems to do with initial condition of the universe. But those will be provided separately in other chance,
2. Introduction to general relativity*
2.1 Summary of general relativity .
The Robertson-Walker metric or line-element is fundamental in the standard models of cosmology. The mathematical framework of the metric is that of general relativity. Here we will summarize general relativity as a reminder of main result and for the sake of completeness. Because [Dirac 1975]*, which is the main source in this chapter, was studied previously here and some contents which are different from the book will be described chiefly.
General relativity is formulated in a four-dimensional Riemannian space in which points are labelled by a general coordinate system (𝑥0, 𝑥1, 𝑥2, 𝑥3), often written as 𝑥𝜇 (𝜇 = 0, 1, 2, 3). In the whole of space-time coordinates, 𝑥0 = 𝑐𝑡 (𝑐: the speed of light, 𝑡: time), 𝑥1 which has distance dimension, 𝑥2 and 𝑥3 which have same dimension and are corresponding to spatial coordinates of three dimensional Euclidean space. According to the law of special relativity, the interaction of material particles takes time of speed of light among them and the law was experimentally proved [Landau-Lifshitz 1975 pp.1~]. If we take a event or a point close to the point of 𝑥𝜇 as 𝑥𝜇 + 𝑑𝑥𝜇, the interval between the two evens or points 𝑑𝑠, which is invariant as follows:
(2.1) 𝑥0 = 𝑐𝑡, 𝑥1 = 𝑥, 𝑥2 = 𝑦, 𝑥3 = 𝑧 (𝑐 = 2.998 x 1010cm/sec); 𝑑𝑠2 = (𝑑𝑥0)2 - (𝑑𝑥1)2 - (𝑑𝑥2)2 - (𝑑𝑥3)2
Any 𝐴𝜇 that transforms under a change of coordinates like as above called a contravariant vector as a four-vector. we define covariant vector 𝐴𝜇 as a four-vector and thus have the scalar product invariant as follows:
(2.2) (𝐴0)2 - (𝐴1)2 - (𝐴2)2 - (𝐴3) 2 = (𝐴, 𝐴); 𝐴0 = 𝐴0, 𝐴1 = -𝐴1, 𝐴2 = -𝐴2, 𝐴3 = -𝐴3; 𝐴𝜇𝐵𝜇 = 𝐴0𝐵0 + 𝐴1𝐵1 + 𝐴2𝐵2 + 𝐴3𝐵3 = (𝐴, 𝐵),
where 𝐴𝜇𝐵𝜇 are sums of a pair of dummy indices at upper and lower indices separately.according to Einstein summation notation enable to simplify complicate tensor equations.
Under a coordinate transformation from 𝑥𝜇 to 𝑥'𝜇 a contravariant vector field 𝐴𝜇, a covariant vector field 𝐵𝜇 and a tensor such as 𝑇𝜇𝜈𝜆 transform as follows:
(2.3) 𝐴'𝜇 = (∂𝑥'𝜇/∂𝑥𝜈) 𝐴𝜈, 𝐵'𝜇 = (∂𝑥𝜈/∂𝑥'𝜇) 𝐵𝜈, 𝑇'𝜇𝜈𝜆 = (∂𝑥'𝜇/∂𝑥𝜌) (∂𝑥𝜎/∂𝑥'𝜈) (∂𝑥𝜏/∂𝑥'𝜆) 𝑇𝜌𝜎𝜏.
All the information about gravitational field is contained in the second rank tensor 𝑔𝜇𝜈 called fundamental tensor or metric tensor which determines the square of space-time intervals 𝑑𝑠2 between infinitesimally separated events or points 𝑥𝜇 and 𝑥𝜇 + 𝑑𝑥𝜇 as follows:
(2.4) 𝑑𝑠2 = 𝑔𝜇𝜈𝑑𝑥𝜇𝑑𝑥𝜈, 𝑔𝜇𝜈 = 𝑔𝜈𝜇. 𝑔𝜇𝜈𝑔𝜈𝜆 = 𝛿𝜆𝜇, 𝛿𝜆𝜇 = 1 for 𝜆 = 𝜇, 𝛿𝜆𝜇 = 0 for 𝜆 ≠ 𝜇,
The contravariant tensor corresponding to 𝑔𝜇𝜈 called inverse metric tensor is denoted by 𝑔𝜇𝜈 and is defined by as above and where the 𝛿𝜆𝜇 is the Kronecker delta, which equals unity if 𝜆 = 𝜇 and zero otherwise. Indices can be raised or lowered or changed by using the metric tensor and Kronecker delta as follows:
(2.5) 𝐴𝜇 = 𝑔𝜇𝜈𝐴𝜈, 𝐴𝜇 = 𝑔𝜇𝜈𝐴𝜈, 𝐴𝜇 = 𝛿𝜇𝜌𝐴𝜌.
The generalization of partial differentiation to Riemannian space is given by covariant differentiation denoted by semi-colon and defined as follows:
(2.6 a, b, c) 𝐴𝜇;𝜈 = ∂𝐴𝜇/∂𝑥𝜈 + 𝛤𝜇𝜈𝜆𝐴𝜆; 𝐴𝜇;𝜈 = ∂𝐴𝜇/∂𝑥𝜈 - 𝛤𝜆𝜇𝜈𝐴𝜆. 𝐴𝜇𝜈𝜆;𝜎 = ∂𝐴𝜇𝜈𝜆/∂𝑥𝜎 + 𝛤𝜇𝜎𝜌𝐴𝜌𝜈𝜆 - 𝛤𝜌𝜈𝜎𝐴𝜇𝜌𝜆 - 𝛤𝜌𝜆𝜎𝐴𝜇𝜈𝜌.
Here the 𝛤𝜇𝜈𝜆 are called Christoffel symbols; their lower indices are interchangeable and are given in terms of metric tensor as follows:
(2.7) 𝛤𝜇𝜈𝜆 = 1/2 𝑔𝜇𝜎(𝑔𝜎𝜇,𝜆 + 𝑔𝜎𝜆,𝜇 - 𝑔𝜈𝜆,𝜎), 𝑔𝜎𝜇,𝜆 ≡ ∂𝑔𝜎𝜇/∂𝑥𝜆; 𝛤𝜇𝜈𝜆 = 𝛤𝜇𝜆𝜈.
Equation (2.7) has the consequence that the covariant derivative of the metric tensor or inverse metric tensor vanishes:
(2.8) 𝑔𝜇𝜈;𝜆 = 0, 𝑔𝜇𝜈;𝜆 = 0.
With metric tensors the indices of vectors in covariant differentiation can be lowered and raised also as folllows:
(2.9) 𝑔𝜎𝜇𝐴𝜇;𝜈 = 𝐴𝜎;𝜈, 𝑔𝜎𝜇𝐴𝜇;𝜈 = 𝐴𝜎;𝜈
Under a coordinate transformation from 𝑥𝜇 to 𝑥'𝜇 the 𝛤𝜇𝜈𝜆 transform as folllows:
(2.10) 𝛤𝜇𝜈𝜆 = (∂𝑥'𝜇/∂𝑥𝜌) (∂𝑥𝜎/∂𝑥'𝜈) (∂𝑥𝜏/∂𝑥'𝜆)𝛤𝜌𝜎𝜏 + (∂2𝑥𝜎/∂𝑥'𝜈𝑥'𝜆) (∂𝑥'𝜇/∂𝑥𝜎),
so the 𝛤𝜇𝜈𝜆 is not a tensor. Therefore at any specific point a coordinate system always be chosen so that the 𝛤𝜇𝜈𝜆 vanish there. From (2,7) it follows that the first derivatives of metric tensor also vanish at the point. This is one form of the equivalence of principle, according to which the gravitational field can be 'transformed away' at any point bt choosing a suitable frame of reference. At this point one can carry out a further transformation of the coordinates to reduce the metric to that of flat (Minkowski) space as (2.1);
(2.11) 𝑑𝑠2 = (𝑑𝑥0)2 - (𝑑𝑥1)2 - (𝑑𝑥2)2 - (𝑑𝑥3)2.
For a covariant vector 𝐴𝜇, in general, two covariant differentiation in succession their order does matter and we get
(2.12) 𝐴𝜇;𝜈;𝜆 - 𝐴𝜇;𝜆;𝜈 = 𝑅𝜎𝜇𝜈𝜆,
where 𝑅𝜎𝜇𝜈𝜆 is called the Riemann(-Christoffel) curvature tensor and defined by
(2.13) 𝑅𝜎𝜇𝜈𝜆 = 𝛤𝜎𝜇𝜆,𝜈 - 𝛤𝜎𝜇𝜈,𝜆 + 𝛤𝜎𝛼𝜈𝛤𝛼𝜇𝜆 - 𝛤𝜎𝛼𝜆𝛤𝛼𝜇𝜈.
The Riemann curvature tensor has the following properties:
(2.14 a, b, c) 𝑅𝜎𝜇𝜈𝜆 = 𝑔𝜎𝛼𝑅𝜎𝛼𝜇𝜈𝜆, 𝑅𝜎𝜇𝜈𝜆 = -𝑅𝜇𝜎𝜈𝜆 = -𝑅𝜎𝜇𝜆𝜈, 𝑅𝜎𝜇𝜈𝜆 = 𝑅𝜈𝜆𝜎𝜇, 𝑅𝜎𝜇𝜈𝜆 + 𝑅𝜎𝜆𝜇𝜈 + 𝑅𝜎𝜈𝜆𝜇 = 0,
and satisfies the Bianchi identity :
(2.15) 𝑅𝜎𝜇𝜈𝜆;𝜌 + 𝑅𝜎𝜇𝜌𝜈;𝜆 + 𝑅𝜎𝜇𝜆𝜌;𝜈 = 0.
The Ricci tensor 𝑅𝜇𝜈 is defined by
(2.16) 𝑅𝜇𝜈 = 𝑔𝜆𝜎𝑅𝜆𝜇𝜎𝜈 = 𝑅𝜎𝜇𝜌𝜈,
From (2.13) and (2.16) 𝑅𝜇𝜈 is given as follows:
(2.17) 𝑅𝜇𝜈 = 𝛤𝜆𝜇𝜈,𝜆 - 𝛤𝜆𝜇𝜆,𝜈 + 𝛤𝜆𝜇𝜈𝛤𝜎𝜆𝜎 - 𝛤𝜎𝜇𝜆𝛤𝜆𝜈𝜎.
Let the determinant of 𝑔𝜇𝜈 considered as a matrix be denoted by 𝑔 which is negative quantity. Then another expression for 𝑅𝜇𝜈 is given by the following:
(2.18) 𝑅𝜇𝜈 = 1/(-𝑔)1/2 [𝛤𝜆𝜇𝜈(-𝑔)1/2],𝜆 - [log(-𝑔)1/2],𝜇𝜈 - 𝛤𝜎𝜇𝜆𝛤𝜆𝜈𝜎.
This follows from (2.7) and the next properties which is proved at [Dirac 1975 p.25]
(2.19) 𝛤𝜆𝜇𝜆 = [log(-𝑔)1/2],𝜇.
From (2.18) it follows that 𝑅𝜇𝜈 = 𝑅𝜈𝜇. Some authors define Riemann curvature tensor and Ricci tensor with opposite signs. The Ricci scalar 𝑅 is defined by
(2.20) 𝑅 = 𝑔𝜇𝜈𝑅𝜇𝜈.
By contracting the Biancchi identity on the pair of indices 𝜇𝜈 and 𝜎𝜌 (that is, multiplying by 𝑔𝜇𝜈 and 𝑔𝜎𝜌). One can deduce the identity
(2.21) (𝑅𝜇𝜈 - 1/2 𝑔𝜇𝜈𝑅);𝜈.
The tensor 𝐺𝜇𝜈 = 𝑅𝜇𝜈 - 1/2 𝑔𝜇𝜈𝑅 is sometimes called the Einstein tensor.
We are now in a position to write down the fundamental equations of general relativity. These are Einstein's equations given by [Landau-Lifshitz 1975 § 95.5]:
(2.22) 𝑅𝜇𝜈 - 1/2 𝑔𝜇𝜈𝑅 = 8𝜋𝐺/𝑐4 𝑇𝜇𝜈,
where 𝑇𝜇𝜈 is the energy-momentum tensor of the source producing the gravitational field and 𝐺 is Newton's gravitational constant. For a perfect fluid, 𝑇𝜇𝜈 takes a following form [Landau-Lifshitz 1975 §94.9]:
(2.23) 𝑇𝜇𝜈 = (𝜌 + 𝑝)𝑢𝜇𝑢𝜈 - 𝑝𝑔𝜇𝜈 or 𝑇𝜇𝜈 = (𝜌 + 𝑝)𝑢𝜇𝑢𝜈 - 𝑝𝑔𝜇𝜈,
where 𝜌 is the mass-energy dnsity, 𝑝 is the pressure and 𝑢𝜇 is the four-velocity of the matter given by
(2.24) 𝑢𝜇 = 𝑑𝑥𝜇/𝑑𝑠,
where 𝑥𝜇(𝑠) describes the worldline of matter in terms of the proper time 𝜏 = 𝑠/𝑐 along the worldline. We will consider some other forms of the energy-momentum tensor than (2.23). Refer to [Dirac 1975 p.45; 𝑇𝜇𝜈 = 𝜌𝜐𝜇𝜐𝜈]. From (2.21) Einstein's equations are compatible with the following equations
(2.25) 𝑇𝜇𝜈;𝜈 = 0,
which is the equation for the conservation of mass-energy and momentum.
The equations of motion of a particle in a gravitational field are
(2.26) 𝑑2𝑥𝜇/𝑑𝑠2 + 𝛤𝜇𝜆𝜈 (𝑑𝑥𝜆/𝑑𝑠) (𝑑𝑥𝜈/𝑑𝑠) = 0.
Geodesics can also be introduced through the concept of parallel transfer. Consider a curve 𝑥𝜇(𝜆), where 𝑥𝜇 are suitably differentiable functions of the real parameter 𝜆, varying over some interval of real time. For an arbitrary vector field 𝑌𝜇 its covariant derivative along the curve is 𝑌𝜇;𝜈(𝑑𝑥𝜈/𝑑𝜆). The 𝑌𝜇 is said to be parallelly transported along the curve if
(2.27) 𝑌𝜇;𝜈(𝑑𝑥𝜈/𝑑𝜆) = 𝑌𝜇,𝜈 (𝑑𝑥𝜈/𝑑𝜆) + 𝛤𝜇𝜈𝜎𝑌𝜎 (𝑑𝑥𝜈/𝑑𝜆) = 𝑑𝑌𝜇/𝑑𝜆 + 𝛤𝜇𝜈𝜎𝑌𝜎 (𝑑𝑥𝜈/𝑑𝜆) = 0.
The curve is said to be a geodesic curve if the tangent vector is transported parallelly, that is, putting (𝑌𝜇 = 𝑑𝑥𝜇/𝑑𝜆), if
(2.28) 𝑑2𝑥𝜇/𝑑𝜆2 + 𝛤𝜇𝜈𝜎 (𝑑𝑥𝜈/𝑑𝜆) (𝑑𝑥𝜎/𝑑𝜆) = 0.
The curve, or a portion of it, is time-like, light-like or space-like according to whether 𝑔𝜇𝜈 (𝑑𝑥𝜇/𝑑𝜆) (𝑑𝑥𝜈/𝑑𝜆) > 0, = 0, or < 0.
2.2 Killing vectors** .
Einstein's exterior equation 𝑅𝜇𝜈 = 0, when 𝑇𝜇𝜈 = 0, are a set of coupled non-linear partial differential equation for the ten unknown unctions 𝑔𝜇𝜈. To determine the simplest form of the metric one has to find some coordinate independent and covariant manner of defining space-time symmetries such as axial symmetry and stationary. This is done with the help of Killing vectors, as these have some relevance for the derivation of the Robertson-Walker metric.
In the following we will sometimes we write 𝑥, 𝑦, 𝑥' for 𝑥𝜇, 𝑦𝜇, 𝑥'𝜇 respectively. A metric 𝑔𝜇𝜈(𝑥) is form-invariant under a transformation from 𝑥𝜇 to 𝑥'𝜇 if 𝑔'𝜇𝜈(𝑥') is the same function of 𝑥'𝜇 as 𝑔𝜇𝜈(𝑥) is of 𝑥𝜇. For example Minkowski metric is form-variant under a Lorentz transformation. Thus [Weinberg 1972 §13.1]
(2.29) 𝑔'𝜇𝜈(𝑦) = 𝑔𝜇𝜈(𝑦), all 𝑦.
Therefore
(2.30 a, b, c) 𝑔'𝜇𝜈(𝑥') = (∂𝑥𝜌/∂𝑥'𝜇) (∂𝑥𝜎/∂𝑥'𝜈) 𝑔𝜇𝜈(𝑥); 𝑔𝜇𝜈(𝑥) = (∂𝑥'𝜌/∂𝑥𝜇) (∂𝑥'𝜎/∂𝑥𝜈) 𝑔'𝜇𝜈(𝑥'); 𝑔𝜇𝜈(𝑥) = (∂𝑥'𝜌/∂𝑥𝜇) (∂𝑥'𝜎/∂𝑥𝜈) 𝑔𝜇𝜈(𝑥')
Any transformation from 𝑥𝜇 to 𝑥'𝜇 that satisfies (2.30 c) is called an isometry. In general, this equation is a very complicated restriction on the function of 𝑥'𝜇(𝑥). Consider an infinitesimal isometry transformation from 𝑥𝜇 to 𝑥'𝜇 defined by
(2.31) 𝑥'𝜇 = 𝑥𝜇 + 𝛼𝜉𝜇(𝑥), with constant ∣𝛼∣ ≪ 1.
with 𝛼 constant and ∣𝛼∣ ≪ 1. Substituting in (2.30 c) and expanding by Taylor's formula and neglecting terms involving 𝛼2 we arrivie at the following equation And this can be written in terms of derivatives of the covariant components 𝜉𝜎 ≡ 𝑔𝜇𝜎𝜉𝜇 with the use of (2.6 b) and (2.7) as follows[Ohanian-Ruffini 1994 §6.8]:
(2.32) 𝑔𝜇𝜎 ∂𝜉𝜇/𝑥𝜇 + 𝑔𝜌𝜇 ∂𝜉𝜇/𝑥𝜎 + (∂𝑔𝜌𝜎/𝑥𝜇) 𝜉𝜇 = 0.
(2.33) 𝜉𝜎;𝜌 + 𝜉𝜌;𝜎 = 0.
Equation (2.33) is Killing's equation and a vector field 𝜉𝜇 satisfying it called a Killing vector of metric 𝑔𝜇𝜈 and 𝜉𝜎;𝜌 called Killing tensor. Thus if there exists a solution of (2.33) for given 𝑔𝜇𝜈, then the corresponding 𝜉𝜇represents an infinitesimal isometry of of metric 𝑔𝜇𝜈 and implies that the metric has a certain symmetry. Because Killing's equation is covariantly expressed, it is a tensor equation and through coordinate transformation a certain isometry which the metric may contain is invariant.
We now derives a property of Killing vectors which we might use later. Let 𝜉(1) and 𝜉(2) be two linearly independent solution of Killing equations (2.33). We define the commutator of them as the vector 𝜁𝜇 given by
(2.34) 𝜁𝜇 ≡ [𝜉(1),𝜉(2)] ≡ 𝜉(1)𝜇;𝜆𝜉(2)𝜆 - 𝜉(2)𝜇;𝜆𝜉(1)𝜆, 𝜁𝜇 = 𝑔𝜇𝜎𝜁𝜎 = 𝑔𝜇𝜎𝜉(1)𝜎;𝜆𝜉(2)𝜆 - 𝑔𝜇𝜎𝜉(2)𝜎;𝜆𝜉(1)𝜆 = 𝜉(1)𝜇;𝜆𝜉(2)𝜆 - 𝜉(2)𝜇;𝜆𝜉(1)𝜆.
We will show that 𝜁𝜇 is also a Killing vector, That is,
(2.35) 𝜁𝜇;𝜈 + 𝜁𝜈;𝜇 = 0.
(2.36) 𝜁𝜇;𝜈 + 𝜁𝜈;𝜇 = 𝜉(1)𝜇;𝜆;𝜈𝜉(2)𝜆 + 𝜉(1)𝜇;𝜆𝜉(2)𝜆;𝜈 - 𝜉(2)𝜇;𝜆;𝜈𝜉(1)𝜆 - 𝜉(2)𝜇;𝜆𝜉(1)𝜆;𝜈 + 𝜉(1)𝜈;𝜆;𝜇𝜉(2)𝜆 + 𝜉(1)𝜈;𝜆𝜉(2)𝜆;𝜇 - 𝜉(2)𝜈;𝜆;𝜇𝜉(1)𝜆 - 𝜉(2)𝜈;𝜆𝜉(1)𝜆;𝜇,
From the the fact thar 𝜉(1), 𝜉(2) are Killing vectors and from (2.12) and (2.14 c), we have
(2.37) 𝜉𝜇;𝜈;𝜆 + 𝜉𝜈;𝜇;𝜆 = 0, 𝜉𝜇;𝜈;𝜆 - 𝜉𝜇;𝜆;𝜈 = 𝜉𝜎𝑅𝜎𝜇𝜈𝜆, 𝑅𝜎𝜇𝜈𝜆 + 𝑅𝜎𝜆𝜇𝜈 + 𝑅𝜎𝜈𝜆𝜇 = 0
(2.38 a, b, c) 𝜉(1)𝜇;𝜆;𝜈𝜉(2)𝜆 + 𝜉(1)𝜈;𝜆;𝜇𝜉(2)𝜆 = 𝜉(1)𝜎𝜉(2)𝜆(𝑅𝜎𝜇𝜆𝜈 + 𝑅𝜎𝜈𝜆𝜇), 𝜉(2)𝜇;𝜆;𝜈𝜉(1)𝜆 + 𝜉(2)𝜈;𝜆;𝜇𝜉(1)𝜆 = 𝜉(2)𝜎𝜉(1)𝜆(𝑅𝜎𝜇𝜆𝜈 + 𝑅𝜎𝜈𝜆𝜇), (23.8 a) - (23.8 b) = 0.
The other terms can be canceled by using Killing's equation. For example
(2.39) 𝜉(1)𝜇;𝜆𝜉(2)𝜆;𝜈 = -𝜉(1)𝜆;𝜇𝜉(2)𝜆;𝜈 = -𝜉(1)𝜆;𝜇𝜉(2)𝜆;𝜈 = +𝜉(1)𝜆;𝜇𝜉(2)𝜈;𝜆,
which cancels the second term and last term in (2.36), and so on. Thus 𝜁𝜇 satisfies (2.35) and so is a Killing vector. Suppose we have only 𝑛 linearly independent Kiilling vectors 𝜉(1)𝜇, 𝑖 = 1, 2, ..., 𝑛 and no more. Then we have the result
(2.40) [𝜉(𝑖),𝜉(𝑗)] = 𝜉(𝑖)𝜇;𝜈𝜉(𝑗)𝜈 - 𝜉(𝑗)𝜇;𝜈𝜉(𝑖)𝜈 = 𝚺𝑘=1𝑛 𝑎𝑖𝑗𝑘 𝜉(𝑘), 𝑖, 𝑗 = 1,..., 𝑛, 𝑎𝑖𝑗𝑘: constants.
* Textbook (Overview): Islam. J.N. An introduction to Mathematical Cosmology (2nd edition, Cambridge University Press 2002)
(Main): M.P. Hobson, G. Efstathiou and A.N. Lasenby General Relativity An Introduction for Physicists (Cambridge University Press 2006)
For General Relativity, refer to P.A.M. Dirac General Theory of Relativity [Dirac 1975], which is at [88] here and thus described briefly.
Also refer to L.D. Landau and E.M. Lifshitz The Classical Theory of Fields (4th edition) [Landau Lifshitz 1975], a classic reference .
** Refer to Steven Weinberg Gravitation and Cosmology [Weinberg 1972], which is one of the best reference for GR with cosmology
Also refer to H.C. Ohanian and R. Ruffini Gravitation and Spacetime [Ohanian Ruffini 1994] describing Killing vectors.
※ attention: some rigorous derivation might be required
p.s. 예고한 대로 세계적 추세에 따라 Mathematical Cosmology(수학적 우주론)를 삼십여 년(!)만에 영어로 기술하기 시작함..ㅎ
이 학습을 시작한 지 꽤 오래됐는데, 도중에 주춤하기도 했으며... 그 사이, S. Weinberg의 <최초의 3분>을 읽었고, 또한, 최근 발간된
D. Fleisch A Student's Guide to the Schrodinger Equation (Cambridge University Press 2020)을 학습하느라 우주론 학습을 잠시 쉬었음.
거기서는 Dirac이 1939년에 만든 bra-ket라는 vector 내적의 일반화된 version-양자역학에는 필수-에 관한 내용이 특히 흥미로웠으며 ...
모호했던 Dual vector, Eigenvector, Eigenvalue, Eigenfunction과 대수학자 이름의 Hilbert space를 이해하게 되었음~
|
|
|





































