|
김관석
|
2024-10-16 19:06:40, 조회수 : 112 |
- Download #1 : BC_6a.jpg (140.6 KB), Download : 0

6 Relativistic Perturbation Theory
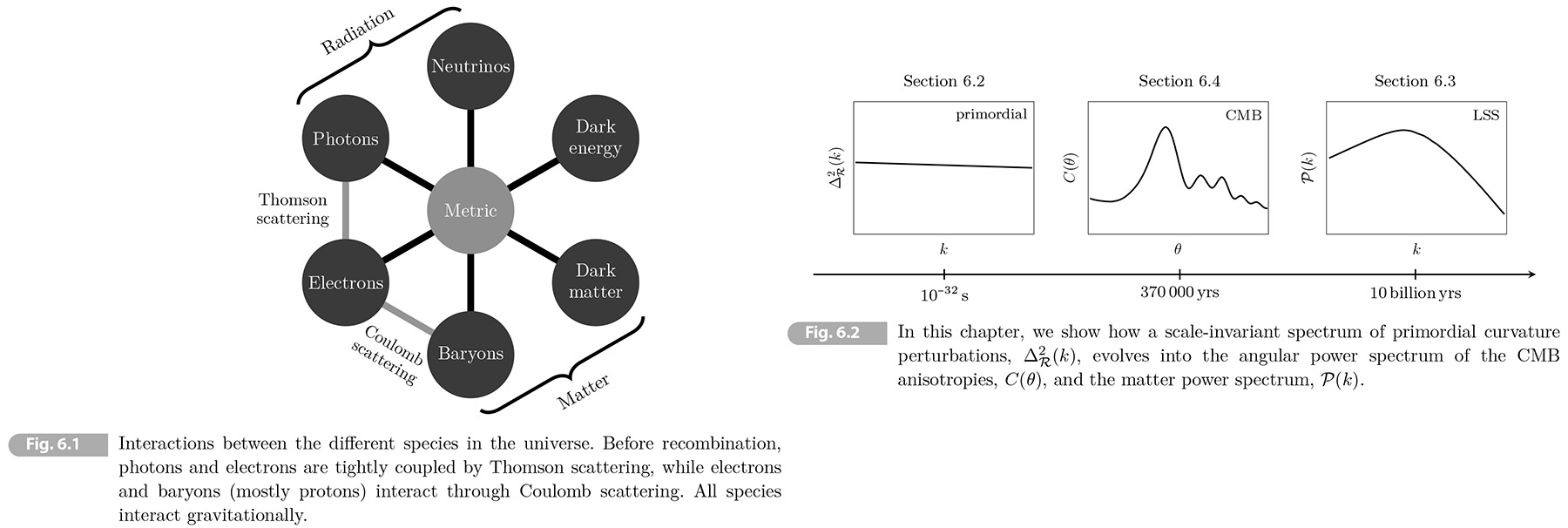
For relativistic fluids (like photons neutrons) and on scales larger than the Hubble radius the correct description requires a general-relativistic treatment which we will develop in this chapter. Fig. 6.1 illustrates the interactions of all known matter species in the universe.
After neutrino decoupling and nucleosynthesis-at low energy-the only significant forces in cosmological evolution were gravity and electromagnetism. By equivalence principle, all species interact through a universal gravitational force. In addition, photon, electrons and protons were strongly coupled by their electromagnetic interactions and could be treated as a single photon-baryon fluid. After recombination, the electromagnetic coupling became insignificant and the evolution was determined by gravity alone. There are two types of gravitational effects: the homogeneous density of the species determines the expansion rate of the universe, while their perturbations source the local gravitational potential. Both of these effects feed back into the into the evolution of the species. This feedback is nonlinear and can lead to rather complex dynamics.
In structure formation matter-radiation equality, 𝑧eq ≈ 3400, and photon decoupling, 𝑧dec ≈ 1100 are two important times. Before equality, the growth structure is suppressed by the large radiation pressure of photons. The clustering of dark matter perturbations only start to become significant when the universe becomes matter dominated. Before decoupling, baryons are tightly coupled to the photons and their density fluctuations oscillate. These oscillation arise because of two opposed forces: gravity and radiation pressure. As gravity makes the perturbations collapse, the radiation pressure increases and causes the perturbation to re-expand. The pressure then drops, so that gravity wins the battle again and the process repeats, leading to sustained oscillations or "sound waves' in the primordial plasma. The frequency depends on wavelength of the fluctuations. At decoupling, modes with different wavelengths are captured at different phases, giving rise to a characteristic pattern in CMB. After decoupling, the baryons lose the pressure support of the photons and fall into the gravitational potential wells created by the dark matter. Eventually, stars and galaxies will form.
* * * We will begin, in Section 1, by defining the perturbations of metric and the energy-momentum tensor. We will show that the form of perturbations depends on the choice of coordinates (or the 'gauge choice"). We will derive the linearized evolution equations in Newtonian gauge and show that, on small scales, they reduce to the previous Newtonian equations.
In Section 6.2, will discuss the initial conditions of perturbations of superhorizon scales. We will introduce the concept of "adiabatic perturbation" and shoe that the "comoving curvature perturbation" 𝓡 is constant outside the horizon. Our task will be to determine how these initial fluctuations give rise to the observed correlations in the late universe (see Fig. 6.2). In Section 6.3, we determine the evolution of matter fluctuations and derive the late-time power spectrum. In Sectin 6.4, we slove for the dynamics of the tightly-coupled photon-baryon fluid before decoupling, and show how it is imprinted in the CMB anisotropies and the matter spectrum (see also Chapter 7).
All numerical computations here ere performed with the Bolitzmann code CLASS1-or the CAMB.2
6.1 Linear Perturbations
Conceptually perturbation theory is GR is the same as in Newtonian gravity. We write the metric and energy momentum tensor as3
(6.1) 𝑔𝜇𝜈(𝑡, 𝐱) = 𝑔̄𝜇𝜈 + 𝛿𝑔𝜇𝜈(𝑡, 𝐱), 𝛵𝜇𝜈(𝑡, 𝐱) = 𝛵̄𝜇𝜈 + 𝛿𝛵𝜇𝜈(𝑡, 𝐱),
and expand ∇𝜇𝛵𝜇𝜈 = 0 and 𝐺 = 8π𝐺𝛵𝜇𝜈 to linear order in perturbations. In practice two features make it more complicated than the Newtonian analysis. First, the algebra is much more involved. To address this challenge we will perform all algebraic manipulations very explicitly and a Mathematica notebook will be provided on the book's website which make us to perform the calculation without any effort. Second, on large scales, there is an ambiguity in what we call matter perturbations and what are metric perturbations-by change of coordinates we can transform on into other. This subtlety did not arise in the Newtonian treatment.
6.1.1 Metric Perturbations
We will take the background metric 𝑔̄𝜇𝜈 to be the flat FRW metric. The perturbed spacetime can be written as
(6.2) 𝑑𝑠2 = 𝑎(𝜂)[-(1 + 2𝛢)𝑑𝜂2 + 2𝛣𝑖𝑑𝑥𝑖𝑑𝜂 + (𝛿𝑖𝑗 + 2𝐸𝑖𝑗)𝑑𝑥𝑖𝑑𝑥𝑗],
where 𝛢, 𝛣𝑖 and 𝐸𝑖𝑗 are functions of space and (conformal) time. The factors of 2 are introduced for later convenience.
It will be extremely useful to perform a scalar-vector-Tensor(SVT) decomposition of the perturbations. We can split any 3-vector into the gradient of a scalar and a divergenceless vector
(6.3) 𝛣𝑖 = ∂𝑖𝛣 + 𝑩𝑖, ∂𝑖𝑩𝑖 = 0
In Fourier space, (6.3) becomes4 𝛣𝑖 = 𝑖𝑘̂𝛣 + 𝑩𝑖, where 𝐤̂ ≡ 𝐤/∣𝐤∣. The vector was split into a piece that is paralleled to 𝐤 and a piece orthogonal to it. Any rank-2 symmetric tensor can be written
(6.4) 𝐸𝑖𝑗 = 𝐶𝛿𝑖𝑗 + ∂⟨𝑖∂𝑗⟩𝐸 + ∂(𝑖𝑬𝑗) + 𝑬𝑖𝑗,
where 𝐶𝛿𝑖𝑗 + ∂⟨𝑖∂𝑗⟩𝐸 is scalar, ∂⟨𝑖𝑬𝑗⟩ is vector and 𝑬𝑖𝑗 is tensor.
(6.5) ∂⟨𝑖∂𝑗⟩𝐸 ≡ (∂𝑖∂𝑗 - 1/3 𝛿𝑖𝑗∇2)𝐸,
(6.6) ∂(𝑖𝑬𝑗) ≡ 1/2 (∂𝑖𝑬𝑗 + ∂𝑗𝑬𝑖).
The first term in (6,4) contains the trace of spatial perturbation, 𝐸𝑖𝑖 = 𝐶𝛿𝑖𝑖 = 3𝐶, while the remaining terms are traceless. As before the hatted quantities have vanishing divergence, ∂𝑖𝑬𝑖 = ∂𝑖𝑬𝑖𝑗 = 0, and so correspond to transverse vector and tensor perturbations. The tensor perturbations describe gravitational waves (see Section 6.5) and following Georgi's dictum5 they are denoted as 𝘩𝑖𝑗 ≡ 2𝑬𝑖𝑗. In Fourier space we write (6.5) as ∂⟨𝑖∂𝑗⟩𝐸 → -(𝑘̂𝑖𝑘̂𝑗 - 1/3 𝛿𝑖𝑗)𝐸 ≡ -𝑘̂⟨𝑖𝑘̂𝑗⟩𝐸.
The 10 degrees of freedom of metric was decomposed into 4+4+2 SVT degrees of freedom:
• scalars: 𝛢, 𝛣, 𝐶, 𝐸 • vectors: 𝑩𝑖, 𝑬𝑖 • tensors: 𝑬𝑖𝑗
What makes the SVT decomposition so powerful is the fact That the Einstein equation for scalars, vectors and tensors don't mix at linear order and can be treated separately. We will mostly be interested in scalar fluctuations and the associated density perturbations , and at linear order it is consistent to set vectors and tensors to zero. Vector perturbations aren't produced by inflation and even if they were, they would decay quickly with the expansion of the universe. Tensor perturbations are an important prediction of inflation and we will discuss them at various point.
Gauge problem
The metric perturbations in (6.2) aren't uniquely defined, bit depends on our choice of coordinate or the gauge choice. Making a different choice of coordinate can change the values of the perturbation variables. It may even "fictitious perturbations." that can arise from an inconvenient choice of coordinates even if the background is perfectly homogeneous.
Consider, for example, a homogeneous FRW spacetime and making the change of the spatial coordinates, 𝑥𝑖 ↦ 𝑥̂𝑖 = 𝑥𝑖 + 𝜉𝑖(𝜂, 𝐱). We assume that 𝜉𝑖 is small, so that it can also be treated as a perturbation. Using 𝑑𝑥𝑖 = 𝑑𝑥̂𝑖 - ∂𝜂𝜉𝑖𝑑𝜂 - ∂𝑘𝜉𝑖𝑑𝑥̂𝑘, the line element becomes
(6.7) 𝑑𝑠2 = 𝑎(𝜂)[-𝑑𝜂2 + 𝛿𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗] = 𝑎(𝜂)[-𝑑𝜂2 - 2𝜉𝑖ʹ𝑑𝑥̂𝑖𝑑𝜂 + (𝛿𝑖𝑗 - 2∂(𝑖𝜉𝑗))𝑑𝑥̂𝑖𝑑𝑥̂𝑗], [verification needed]
where we dropped the quadratic terms in 𝜉𝑖 and defined 𝜉𝑖ʹ ≡ ∂𝜂𝜉𝑖. We apparently introduced the metric perturbations 𝛣𝑖 = -𝜉𝑖ʹ and 𝐸̂𝑖 = -𝜉𝑖. These are just fictitious gauge modes that can be removed by going back to the old coordinates.
As another example, consider a change in the time slicing, 𝜂 ↦ 𝜂̂ = 𝜂 + 𝜉0(𝜂, 𝐱). The homogeneous density of the universe then gets perturbed,
(6.8) 𝜌(𝜂) = 𝜌[𝜂̂ - 𝜉0(𝜂, 𝐱)] = 𝜌̄(𝜂̂) - 𝜌̄ʹ𝜉0. [Wikipedia Taylor expansion]
A local change of the time coordinate can introduce a fictitious density perturbation 𝛿𝜌 = -𝜌̄ʹ𝜉0. Conversely, we can remove a real perturbation in the energy density by choosing hypersurface of constant time to coincide with that of constant energy density. We then have 𝛿𝜌 = 0 although there are real inhomogeneities. The fluctuations haven't disappear completely, but will manifest themselves as new perturbations in the metric.
So when the perturbations don't change under a change of coordinates, we can identify true perturbations more conveniently.
Coordinate transformations
Consider the following coordinate transformation
(6.9) 𝑥𝜇(𝑞) ↦ 𝑥̂𝜇(𝑞) ≡ 𝑥𝜇(𝑞) + 𝜉𝜇(𝑞), where 𝜉0 ≡ 𝛵, 𝜉𝑖 ≡ 𝐿𝑖 = ∂𝑖𝐿 + 𝑳𝑖.
The old and new coordinates are evaluated as the same physical point. 𝜉𝜇 can be treated as perturbation. 𝛵(𝜂, 𝐱) defines the hypersurfaces of constant time in the new coordinates, while 𝐿𝑖 determines the spatial coordinates there. We can split the spatial shift 𝐿𝑖 into a scalar 𝐿 and a divergenceless vector 𝑳𝑖.
Consider the transformation of a (Lorentz) scalar field 𝜙(𝜂, 𝐱) which may be the inflaton or the density of a fluid. Since we have only relabelled the coordinate, the value of the field at each point 𝑞 must be unchanged
(6.10) 𝜙(𝑥𝜇) = 𝜙̂(𝑥̂𝜇).
In terms of the background value of the field and its perturbation, we get
(6.11) 𝜙̄(𝜂) + 𝛿𝜙(𝑥𝜇) = 𝜙̄(𝜂̂) + 𝛿𝜙̂(𝑥̂𝜇) = 𝜙̄(𝜂 + 𝛵) + 𝛿𝜙̂(𝑥̂𝜇)
Doing Taylor expanding on the right-hand side, we find [Taylor expanding: 𝑓(𝛵 + 𝜂) = 𝑓(𝜂) + 𝛵𝑓ʹ(𝜂) + 1/2 𝛵2𝑓ʺ(𝜂) + ∙ ∙ ∙ ]
(6.12-4) 𝜙̄(𝜂) + 𝛿𝜙(𝑥𝜇) = 𝜙̄(𝜂) + 𝜙̄ʹ𝛵 + 𝛿𝜙̂(𝑥𝜇). ⇒ 𝛿𝜙̂(𝑥𝜇) = 𝛿𝜙(𝑥𝜇) - 𝜙̄ʹ𝛵(𝑥𝜇). ⇒ 𝛿𝜙̂ = 𝛿𝜙 - 𝜙̄ʹ𝛵.
Note that the both sides are evaluated at the same value 𝑥𝜇 which in general do not correspond to the same physical point and the perturbations only depends on the choice of temporal gauge.
To determine the transformation of the metric, we use the invariant spacetime interval:
(6.15) 𝑑𝑠2 = 𝑔𝜇𝜈(𝑥)𝑑𝑥𝜇𝑑𝑥𝜈 = 𝑔̂𝛼𝛽(𝑥̂)𝑑𝑥̂𝛼𝑑𝑥̂𝛽.
Writing 𝑑𝑥̂𝛼 = (∂𝑥̂𝛼/∂𝑥𝜇)𝑑𝑥𝜇 and similarly for 𝑑𝑥̂𝛽, we find
(6.16) 𝑔𝜇𝜈(𝑥) = ∂𝑥̂𝛼/∂𝑥𝜇 ∂𝑥̂𝛽/∂𝑥𝜈 𝑔̂𝛼𝛽(𝑥̂).
This relates the metric in the old coordinates 𝑔𝜇𝜈 to the new 𝑔̂𝛼𝛽. Given the transformation (6.9) we have in 2 × 2 matrix
(6.17) ∂𝑥̂𝛼/∂𝑥𝜇 = ⌈ ∂𝜂̂/∂𝜂 ∂𝜂̂/∂𝑥𝑗 ⌉ = ⌈ 1 + 𝛵ʹ ∂𝑖𝛵 ⌉ * ipad view
⌊ ∂𝑥̂𝑖/∂𝜂 ∂𝑥̂𝑖/∂𝑥𝑗⌋ ⌊ 𝐿𝑖ʹ 𝛿𝑖𝑗 + ∂𝑗𝐿𝑖 ⌋
(6.17) ∂𝑥̂𝛼/∂𝑥𝜇 = ⌈ ∂𝜂̂/∂𝜂 ∂𝜂̂/∂𝑥𝑗 ⌉ = ⌈ 1 + 𝛵ʹ ∂𝑖𝛵 ⌉ * pc view
⌊ ∂𝑥̂𝑖/∂𝜂 ∂𝑥̂𝑖/∂𝑥𝑗 ⌋ ⌊ 𝐿𝑖ʹ 𝛿𝑖𝑗 + ∂𝑗𝐿𝑖 ⌋
where 𝛼 labels the rows and 𝜇 the columns. In terms of the SVT decomposition, (6.16) implies the followings for the transformation of the metric perturbations in (6.2).
(6.18-9) 𝛢 ↦ 𝛢˜ = 𝛢 - 𝛵ʹ - 𝓗𝛵, 𝛣 ↦ 𝛣˜ = 𝛣 + 𝛵 - 𝐿ʹ, 𝑩𝑖 ↦ 𝑩𝑖˜ = 𝑩𝑖 - 𝑳𝑖ʹ
(6.20-1) 𝐶 ↦ 𝐶˜ = 𝐶 - 𝓗𝛵 - 1/3 ∇2𝐿, 𝐸 ↦ 𝐸˜ = 𝐸 - 𝐿, 𝑬𝑖 ↦ 𝑬𝑖˜ = 𝑬𝑖 - 𝑳𝑖, 𝑬𝑖𝑗 ↦ 𝑬𝑖𝑗.
Example Consider 𝜇 = 𝜈 = 0 in (6.16):
(6.22) 𝑔00(𝑥) = ∂𝑥̂𝛼/∂𝜂 ∂𝑥̂𝛽/∂𝜂 𝑔̂𝛼𝛽(𝑥̂).
Consider 𝛼 = 0 and 𝛽 = 𝑖. The off-diagonal component of the metric 𝑔̂0𝑖 is proportional to 𝑩𝑖˜, so it's a first order perturbation. But ∂𝑥̂𝑖/∂𝜂 is second order and can be neglected. A similar argument holds for 𝛼 = 𝑖 and 𝛽 = 𝑗. So (6.22) reduces to
(6.23) 𝑔00(𝑥) = (∂𝜂̂/∂𝜂)2 = 𝑔̂00(𝑥̂).
Substituting (6.2), (6.9) and (6.17), we get
(6.24-5) 𝑎2(𝜂)(1 + 2𝛢) = (1 + 𝛵ʹ)2𝑎2(𝜂 + 𝛵)(1 + 2𝛢˜) = (1 + 2𝛵ʹ + ∙ ∙ ∙ )(𝑎(𝜂) + 𝑎ʹ𝛵 + ∙ ∙ ∙ )2(1 + 2𝛢˜)
= 𝑎2(𝜂)(1 + 2𝓗𝛵 + 2𝛵ʹ + 2𝛢˜ + ∙ ∙ ∙ ). ⇒ 𝛢 ↦ 𝛢˜ = 𝛢 - 𝛵ʹ - 𝓗𝛵. ▮
Exercise 6.1 Show that the other metric components transform as
(6.26) 𝛣𝑖 ↦ 𝛣𝑖˜ = 𝛣𝑖 + ∂𝑖𝛵 - 𝐿𝑖ʹ,
(6.27) 𝐸𝑖𝑗 ↦ 𝐸𝑖𝑗˜ = 𝐸𝑖𝑗 - 𝓗𝛵𝛿𝑖𝑗 - ∂(𝑖𝐿𝑗).
[Solution] The transformation of the 0𝑖-component of the metric is, [RE (6.2) (6.9) (6.16) (6.17)]
(a) 𝑔0𝑖(𝑥) = ∂𝑥̂𝛼/∂𝜂 ∂𝑥̂𝛽/∂𝑥𝑖 𝑔̂𝛼𝛽(𝑥̂) = ∂𝜂̂/∂𝜂 [∂𝜂̂/∂𝑥𝑖 𝑔̂00(𝑥̂) + ∂𝑥̂𝑗/∂𝑥𝑖 𝑔̂0𝑗(𝑥̂)] + ∂𝑥̂𝑗/∂𝜂 [∂𝜂̂/∂𝑥𝑖 𝑔̂𝑗0(𝑥̂) + ∂𝑥̂𝑘/∂𝑥𝑖 𝑔̂𝑗𝑘(𝑥̂)]
= (1 + 𝛵ʹ)[∂𝑖𝛵𝑔̂00(𝑥̂) + (𝛿𝑗𝑖 + ∂𝑗𝐿𝑖)𝑔̂0𝑗(𝑥̂)] + 𝐿𝑗ʹ[∂𝑖𝛵𝑔̂𝑗0(𝑥̂) + (𝛿𝑘𝑖 + ∂𝑖𝐿𝑘)𝑔̂𝑗𝑘(𝑥̂)] = 𝑔̂0𝑖(𝑥̂) + ∂𝑖𝛵𝑔̂00(𝑥̂) + 𝐿𝑖ʹ𝑔̂𝑖𝑗(𝑥̂) + 𝑂(2).
Substituting the perturbed metric components on both sides, we get [𝑔0𝑖(𝑥) = 𝛣𝑖, 𝑔̂0𝑖(𝑥̂) = 𝛣˜𝑖, 𝑔̂00 = -1, 𝑔̂𝑖𝑗 = 1]
(b) 𝛣𝑖 = 𝛣˜𝑖 - ∂𝑖𝛵 + 𝐿𝑖ʹ ⇒ 𝛣𝑖 ↦ 𝛣𝑖˜ = 𝛣𝑖 + ∂𝑖𝛵 - 𝐿𝑖ʹ ⇒ 𝛣 ↦ 𝛣˜ = 𝛣 + 𝛵 - 𝐿ʹ, 𝑩𝑖 ↦ 𝑩˜𝑖 = 𝑩𝑖 - 𝑳𝑖. ▮
The transformation of 𝑖𝑗-component of metric is
(c) 𝑔𝑖𝑗(𝑥) = ∂𝑥̂𝑘/∂𝑥𝑖 ∂𝑥̂𝑙/∂𝑥𝑗 𝑔̂𝑘𝑙(𝑥̂) = ∂𝑥̂𝛼/∂𝑥𝑖 ∂𝑥̂𝛽/∂𝑥𝑗 𝑔̂𝛼𝛽(𝑥̂) + 𝑂(2) = (𝛿𝑘𝑖 + ∂𝑖𝐿𝑘)(𝛿𝑖𝑗 + ∂𝑗𝐿𝑙) 𝑔̂𝑘𝑙(𝑥̂) = 𝑔̂𝑖𝑗(𝑥̂) + ∂𝑖𝐿𝑘𝑔̂𝑘𝑗(𝑥̂) + ∂𝑗𝐿𝑙𝑔̂𝑖𝑙(𝑥̂).
Substituting the perturbed metric component on both sides, we get [RE (6.2)(6.9) (6.11-2)(c)]
(d) 𝑎2(𝛿𝑖𝑗 + 2𝐸𝑖𝑗) = 𝑎2(𝜂 + 𝛵)(𝛿𝑖𝑗 + 2𝐸˜𝑖𝑗) + 𝑎(𝜂)(∂𝑖𝐿𝑘𝛿𝑘𝑗 + ∂𝑗𝐿𝑙𝛿𝑖𝑙) = 𝑎2(1 + 2𝑎ʹ/𝑎𝛵)(𝛿𝑖𝑗 + 2𝐸˜𝑖𝑗) + 2𝑎2∂(𝑖𝐿𝑗) =
= 𝑎2(𝛿𝑖𝑗 + 2𝐸˜𝑖𝑗) + 2𝑎2𝓗𝛵𝛿𝑖𝑗 + 2𝑎2∂(𝑖𝐿𝑗) + 𝑂(2). ⇒ 𝐸𝑖𝑗 ↦ 𝐸˜𝑖𝑗 = 𝐸𝑖𝑗 - 𝓗𝛵𝛿𝑖𝑗 - ∂(𝑖𝐿𝑗). ▮
In terms of the SVT decomposition of 𝐸𝑖𝑗, this implies [RE (6.4-6)]
(e) 𝐶 ↦ 𝐶˜ = 𝐶 - 𝓗𝛵 - 1/3 ∇2𝐿, 𝐸 ↦ 𝐸˜ = 𝛣 + 𝛵 - 𝐿ʹ, 𝑬𝑖 ↦ 𝑬˜𝑖 = 𝑬𝑖 - 𝑳𝑖, 𝑬𝑖𝑗 ↦ 𝑬𝑖𝑗. ▮
Gauge-invariant variables
One way to avoid the gauge problem is define special combinations of the metric perturbation that do not transform under a change of coordinates. These are so-called Bardeen variables [1]
(6.28) 𝛹 ≡ 𝛢 + 𝓗(𝛣 - 𝐸ʹ) + (𝛣 - 𝐸ʹ)ʹ, 𝜱𝑖 ≡ 𝑩𝑖 - 𝑬𝑖ʹ, 𝑬𝑖𝑗, 𝛷 ≡ -𝐶 + 1/3 ∇2𝐸 - 𝓗(𝛣 - 𝐸ʹ).
These gauge-invariant variables are the 'real' spacetime perturbations since they cannot be removed by a gauge transformation.
Exercise 6.2 Show that 𝛹, 𝛷 and 𝜱𝑖 are gauge invariant. Explain why the tensor perturbation 𝐸̂𝑖𝑗 is gauge invariant at linear order.
[Solution] Under a coordinate transformation, scalar metric perturbation change [RE (6.18-21)]
(a) 𝛹 ≡ 𝛢 + 𝓗(𝛣 - 𝐸ʹ) + (𝛣 - 𝐸ʹ)ʹ ↦ 𝛢 - 𝛵ʹ - 𝓗𝛵 + 𝓗[(𝛣 + 𝛵 - 𝐿ʹ) - (𝐸ʹ - 𝐿ʹ)] + (𝛣 + 𝛵 - 𝐸ʹ)ʹ = 𝛢 + 𝓗(𝛣 - 𝐸ʹ) + (𝛣 - 𝐸ʹ)ʹ = 𝛹.
(b) 𝛷 ≡ -𝐶 + 1/3 ∇2𝐸 - 𝓗(𝛣 - 𝐸ʹ) ↦ -𝐶 + 𝓗𝛵 + 1/3 ∇2𝐿 + 1/3 ∇2(𝐸 - 𝐿) - 𝓗(𝛣 + 𝛵 - 𝐸ʹ) = -𝐶 + 1/3 ∇2𝐸 - 𝓗(𝛣 - 𝐸ʹ) = 𝛷.
(c) 𝜱𝑖 ≡ 𝑩𝑖 - 𝑬𝑖ʹ ↦ (𝑩𝑖 - 𝑳𝑖) - 𝑬𝑖 - 𝑳𝑖 = 𝑩𝑖 - 𝑬𝑖ʹ = 𝜱𝑖.
Because the gauge transform only involves two scalar modes and one vector mode, tensor mode doen't transform at linear order. A tensor mode in the gauge transform would only arise at second order. ▮
Gauge fixing
An alternative solution to gauge problem is to fix the gauge and keep track of all perturbations in both the metric and the matter. A convenient choice of gauge often simplify the analysis. The following are popular gauge:
• Newtonian gauge We can use the freedom in function 𝛵 and 𝐿 in (6.9) to set two of four scalar metric perturbations to zero. The Newtonian gauge is defined by the choice and so (6.2) becomes
(6.29-30) 𝛣 = 𝐸 = 0, ⇒ 𝑑𝑠2 = 𝑎(𝜂)[-(1 + 2𝛹)𝑑𝜂2 + (1 - 2𝛷)𝛿𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗],
where 𝛢 ≡ 𝛹 and 𝐶 ≡ -𝛷 to make contact with the Bardeen potential in (6.28). In this metric hypersurfaces of constant time are orthogonal to the worldlines of observers at rest (since 𝛣 = 0) and the induced geometry is isotropic (since 𝐸 = 0). Notice that the similarity to the usual weak-field limit of GR (Appendix A) with 𝛹 as the gravitational potential. Newtonian gauge will be our preferred one for structure formation.
• Spatially flat gauge This is a convenient gauge for computing inflationary perturbations, by inflaton field 𝛿𝜙 (see Chapter 8), with
(6.31) 𝐶 = 𝐸 = 0,
• Synchronous gauge It is a historically important gauge introduced by Lifshitz in his pioneering work on perturbation [4] -, with
(6.32) 𝛢 = 𝛣 = 0.
But this gauge still contain spurious gauge of freedom. These mode caused some confusion in the early history of cosmological perturbation theory and indeed were the motivation for Bardeen's gauge-invariant approach [1].
6.1.2 Matter Perturbations
We consider perturbations of the energy-momentum tensor.
(6.33) 𝛵00 ≡ -(𝜌̄ + 𝛿𝜌), 𝛵0𝑖 ≡ (𝜌̄ + 𝑃̄)𝑣𝑖, 𝛵𝑖𝑗 ≡ (𝑃̄ + 𝛿𝑃)𝛿𝑖𝑗 + 𝛱𝑖𝑗, 𝛱𝑖𝑖 ≡ 0,
where 𝑣𝑖 is the bulk velocity and 𝛱𝑖𝑖 is the anisotropic stress. Note that 𝛵0𝑖 and 𝛵𝑖0 differ by sign. This is necessary in order for 𝛵0𝑖 = 𝛵𝑖0 to hold. We will write the momentum density as 𝑞𝑖 ≡ (𝜌̄ + 𝑃̄)𝑣𝑖. If there are several contributions to the energy-momentum tensor (e.g. photons,, baryon, dark matter etc.), they are added 𝛵𝜇𝜈 = ∑𝑎𝛵𝜇𝜈 (𝑎), so that
(6.34) 𝛿𝜌 = ∑𝑎𝛿𝜌𝑎, 𝛿𝑃 = ∑𝑎𝛿𝑃𝑎, 𝑞𝑖 = ∑𝑎𝑞𝑖(𝑎), 𝛱𝑖𝑗 = ∑𝑎𝑖𝑗(𝑎).
Note that only the velocities do not add, but momentum densities do.
Exercise 6.3 Given 𝑈̄𝜇 = 𝑎-1(1, 0, 0, 0) and 𝑔𝜇𝜈𝑈𝜇𝑈𝜈 = -1, show that the perturbed 4-velocity must take the form
(6.35-6) 𝑈𝜇 = 𝑎-1(1- 𝛢, 𝑣𝑖), 𝑈𝜇 = 𝑎-1[-(1 + 𝛢), 𝑣𝑖 + 𝛣𝑖],
where 𝛢 and 𝛣𝑖 are defined in (6.2) and 𝑣𝑖 is the bulk velocity. Substituting these results into the perturbed energy-momentum tensor of a fluid,
(6.37) 𝛿𝛵𝜇𝜈 = (𝛿𝜌 + 𝛿𝛲)𝑈̄𝜇𝑈̄𝜈 + (𝜌̄ + 𝑃̄)(𝛿𝑈̄𝜇𝑈̄𝜈 + 𝑈̄𝜇𝛿𝑈̄𝜈) + 𝛿𝛲𝛿𝜇𝜈 + 𝛱𝜇𝜈,
with 𝑈𝜇𝛱𝜇𝜈 = 0, show that this leads to the same result as in (6.33). Show also that 𝛵0𝑖 = (𝜌̄ + 𝑃̄)(𝑣𝑖 + 𝛣𝑖).
[Solution] From 𝑔𝜇𝜈𝑈𝜇𝑈𝜈 = 𝑈𝜈𝑈𝜈 = -1, so we have 𝑈̄𝜇 = 𝑎(-1, 0, 0, 0).
(a) -1 = 𝑔𝜇𝜈𝑈𝜇𝑈𝜈 = 𝑔̄𝜇𝜈𝑈̄𝜇𝑈̄𝜈 + 𝛿𝑔𝜇𝜈𝑈̄𝜇𝑈̄𝜈 + 2𝑔̄𝜇𝜈𝑈̄𝜇𝛿𝑈𝜈 + 𝑂(2) = -1 + 𝑎-2𝛿𝑔00 + 2𝑎-1𝑔̄00𝛿𝑈0 ⇒ 𝛿𝑈0 = -1/2 𝑎-1 𝛿𝑔00/𝑔̄00 = -𝑎-1𝛢.
Since 𝛿𝑈𝑖 is unconstrained, so we define 𝛿𝑈𝑖 ≡ 𝑎-1𝑣𝑖. The perturbed 4-velocity is
(b) 𝑈̄𝜇 = 𝑎-1(1 - 𝛢, 𝑣𝑖).
(c) 𝑈̄𝜇 = 𝑔𝜇𝜈𝑈𝜈 = 𝑔̄𝜇𝜈𝑈̄𝜈 + 𝛿𝑔𝜇𝜈𝑈̄𝜈 + 𝑔̄𝜇𝜈𝛿𝑈𝜈 + 𝑂(2) = 𝑎-1𝑔̄𝜇0 + 𝑎-1𝛿𝑔𝜇0 - 𝑎-1𝑔̄𝜇0𝛢 + 𝑎-1𝑔̄𝜇𝑗𝑣𝑗 = -𝑎𝛿𝜇0 - 2𝑎𝛢𝛿𝜇0 + 𝑎𝛢𝛿𝜇0 + 𝑎𝛣𝑖𝛿𝜇𝑖 + 𝑎𝑣𝑖𝛿𝜇𝑖
(d) 𝑈̄0 = -𝑎(1 + 𝛢), 𝑈̄𝑖 = 𝑎(𝛣𝑖 + 𝑣𝑖), 𝑈̄𝜇 = 𝑎[-(1 + 𝛢), 𝑣𝑖 + 𝛣𝑖].
(e) 𝛿𝛵00 = -(𝛿𝜌 + 𝛿𝛲) + (𝜌̄ + 𝑃̄)(𝛢 - 𝛢) + 𝛿𝛲 + 0 = -𝛿𝜌, 𝛿𝛵𝑖0 = 0 + (𝜌̄ + 𝑃̄)(𝛿𝑈̄𝑖𝑈̄0 + 0) + 0 + 0 = -(𝜌̄ + 𝑃̄)𝑣𝑖,
𝛿𝛵0𝑖 = 0 + (𝜌̄ + 𝑃̄)(0 + 𝑈̄0𝛿𝑈̄𝑖) + 0 + 0 = (𝜌̄ + 𝑃̄)(𝑣𝑖 + 𝛣𝑖), 𝛿𝛵𝑖𝑗 = 0 + (𝜌̄ + 𝑃̄)(0 + 0) + 𝛿𝛲𝛿𝑖𝑗 + 𝛱𝑖𝑗 = 𝛿𝛲𝛿𝑖𝑗 + 𝛱𝑖𝑗, ▮
As for the metric, we apply a SVT decomposition here: 𝛿𝜌 and 𝛿𝑃 have scalar part only, while 𝑣𝑖 and 𝑞𝑖 have scalar and vector parts,
(6.38) 𝑣𝑖 = ∂𝑖𝑣 + 𝐯𝑖, 𝑞𝑖 = ∂𝑖𝑞 + 𝐪𝑖.
The scalar part of the velocity is sometimes written in terms of the velocity divergence, 𝜃 ≡ ∂𝑖𝑣𝑖 = ∇2𝑣.[verification needed] The anisotropic stress 𝛱𝑖𝑗 has
(6.39) 𝛱𝑖𝑗 = ∂⟨𝑖∂𝑗⟩𝛱 + ∂(𝑖𝜫𝑗) + 𝜫𝑖𝑗.
Sometimes it is useful to work with the rescaled anisotropic stress [2], 𝜎 ≡ 2/3 (𝜌̄ + 𝑃̄)-1𝛱. Finally it also convenient to use the density contrast, 𝛿 ≡ 𝛿𝜌/𝜌. Perturbation theory applies when 𝛿 < 1.
Coordinate transformations
Under a coordinate transformation, 𝑥𝜇 ↦ 𝑥̂𝜇, the tensor 𝛵𝜇𝜈 transform as
(6.40) 𝛵𝜇𝜈(𝑥) = ∂𝑥𝜇/∂𝑥̂𝛼 ∂𝑥̂𝛽/∂𝑥𝜈 𝛵˜𝛼𝛽(𝑥̂).
The origin of the transformation law is explained in Section A.3.3. To evaluate it we require ∂𝑥𝜇/∂𝑥̂𝛼 which is the inverse matrix of ∂𝑥̂𝛼/∂𝑥𝜇 since
(6.41) ∂𝑥𝜇/∂𝑥̂𝛼 ∂𝑥̂𝛼/∂𝑥𝜈 = 𝛿𝜇𝜈.
For the transformation in (6.9) the matrix ∂𝑥̂𝛼/∂𝑥𝜇 was given by (6.17):
(6.42) ∂𝑥̂𝛼/∂𝑥𝜇 = ⌈ ∂𝜂̂/∂𝜂 ∂𝜂̂/∂𝑥𝑗 ⌉ = ⌈ 1 + 𝛵ʹ ∂𝑖𝛵 ⌉ * ipad view
⌊ ∂𝑥̂𝑖/∂𝜂 ∂𝑥̂𝑖/∂𝑥𝑗⌋ ⌊ 𝐿𝑖ʹ 𝛿𝑖𝑗 + ∂𝑗𝐿𝑖 ⌋
(6.42) ∂𝑥̂𝛼/∂𝑥𝜇 = ⌈ ∂𝜂̂/∂𝜂 ∂𝜂̂/∂𝑥𝑗 ⌉ = ⌈ 1 + 𝛵ʹ ∂𝑖𝛵 ⌉ * pc view
⌊ ∂𝑥̂𝑖/∂𝜂 ∂𝑥̂𝑖/∂𝑥𝑗 ⌋ ⌊ 𝐿𝑖ʹ 𝛿𝑖𝑗 + ∂𝑗𝐿𝑖 ⌋
To determine the corresponding matrix, we make use of the fact that the inverse of a matrix of the form 𝟏 + 𝜀, where 𝟏 is the identity and 𝜀 is a small perturbation, is 𝟏 - 𝜀 to first order in 𝜀. It follows that
(6.43) ∂𝑥𝜇/∂𝑥̂𝛼 = ⌈ ∂𝜂/∂𝜂̂ ∂𝜂/∂𝑥̂𝑗 ⌉ = ⌈ 1 - 𝛵ʹ -∂𝑖𝛵 ⌉ * ipad view
⌊ ∂𝑥𝑖/∂𝜂 ∂𝑥𝑖/∂𝑥̂𝑗⌋ ⌊ -𝐿𝑖ʹ 𝛿𝑖𝑗 - ∂𝑗𝐿𝑖 ⌋
(6.43) ∂𝑥𝜇/∂𝑥̂𝛼 = ⌈ ∂𝜂/∂𝜂̂ ∂𝜂/∂𝑥̂𝑗 ⌉ = ⌈ 1 - 𝛵ʹ -∂𝑖𝛵 ⌉ * pc view
⌊ ∂𝑥𝑖/∂𝜂 ∂𝑥𝑖/∂𝑥̂𝑗 ⌋ ⌊ -𝐿𝑖ʹ 𝛿𝑖𝑗 - ∂𝑗𝐿𝑖 ⌋
Substituting these result into (6.40), we can determine how the perturbation of the energy-momentum tensor transform.
(6.44-48) 𝛿𝜌 ↦ 𝛿𝜌 - 𝜌̄𝛵, 𝛿𝑃 ↦ 𝛿𝑃 - 𝑃̄𝛵, 𝑞𝑖 ↦ (𝜌̄ + 𝑃̄)𝐿𝑖ʹ, 𝑣𝑖 ↦ 𝑣𝑖 + 𝐿𝑖ʹ, 𝛱𝑖𝑗 ↦ 𝛱𝑖𝑗.
Note that the density and pressure perturbations transform in the same way as the scalar fields in (6.14), since 𝛿𝜌 and 𝛿𝑃 are both Lorentz scalars. [Wikipedia Lorentz scalar]
Example Applying (6.40) to the temporal component of the energy-momentum tensor, we get
(6.49) 𝛵00(𝑥) = ∂𝜂/∂𝑥̂𝛼 ∂𝑥̂𝛽/∂𝜂 𝛵˜𝛼𝛽(𝑥̂) = ∂𝜂/∂𝜂̂ ∂𝜂̂/∂𝜂 𝛵˜00(𝑥̂) + 𝛰(2).
Substituting 𝛵00(𝑥) = -(𝜌̄ + 𝛿𝜌) on both sides, we get
(6.50) 𝜌̄ + 𝛿𝜌 = (1 - 𝛵ʹ)(1 + 𝛵ʹ)[𝜌̄(𝜂 + 𝛵) + 𝛿𝜌̄(𝑥)] = 𝜌̄(𝜂) + 𝜌̄ʹ𝛵 + 𝛿𝜌̄(𝑥) + 𝛰(2).
Solving this for 𝛿𝜌̄ gives
(6.51) 𝛿𝜌̄ = 𝛿𝜌 - 𝜌̄ʹ𝛵,
which agrees with the result in (6.44).
Exercise 6.4 Derive (6.45)-(6.48)
[Solution] Applying (6.40) to the 𝑖𝑗-components, we get for the first term
(a) 𝛵𝑖𝑗(𝑥) = ∂𝑥𝑖/∂𝑥̂𝛼 ∂𝑥̂𝛽/∂𝑥𝑗 𝛵˜𝛼𝛽(𝑥̂) = ∂𝑥𝑖/∂𝑥̂𝑘 ∂𝑥̂𝑙/∂𝑥𝑗 𝛵˜𝑘𝑙(𝑥̂) = (𝛿𝑖𝑘 - ∂𝑘𝐿𝑖)(𝛿𝑘𝑗 + ∂𝑗𝐿𝑘) 𝛵˜𝑘𝑙(𝑥̂),
Substituting 𝛵𝑖𝑗 = -(𝑃̄ + 𝛿𝑃̄)𝑖𝑗 on both sides, we get
(b) (𝑃̄ + 𝛿𝑃)𝛿𝑖𝑗 = (𝛿𝑖𝑘 - ∂𝑘𝐿𝑖)(𝛿𝑘𝑗 + ∂𝑗𝐿𝑘)[𝑃̄(𝜂 + 𝛵) + 𝛿𝑃̄]𝛿𝑘𝑙 = [𝑃̄(𝜂) +𝑃̄ʹ𝛵 + 𝛿𝑃̄]𝛿𝑖𝑗 + 𝛰(2). ⇒
(c) 𝛿𝑃 ↦ 𝛿𝑃 - 𝑃̄ʹ𝛵.
Applying (6.40) to the 𝑖𝑗-components, we get for the second term
(d) 𝛵𝑖𝑗(𝑥) = 𝛱𝑖𝑗 ⇒ 𝛱𝑖𝑗 = (𝛿𝑖𝑘 - ∂𝑘𝐿𝑖)(𝛿𝑘𝑗 + ∂𝑗𝐿𝑘) 𝛱̂𝑘𝑙 = 𝛱𝑖𝑗 + 𝛰(2), 𝛱𝑖𝑗 ↦ 𝛱𝑖𝑗.
Applying (6.40) to the 𝑖0-components, we get
(e) 𝛵𝑖0(𝑥) = ∂𝑥𝑖/∂𝑥̂𝛼 ∂𝑥̂𝛽/∂𝑥0 𝛵˜𝛼𝛽(𝑥̂) = ∂𝑥𝑖/∂𝜂̂ (∂𝜂̂/∂𝜂 𝛵˜00 + ∂𝑥̂𝑘/∂𝜂 𝛵˜0𝑘) + ∂𝑥𝑖/∂𝑥̂𝑗 (∂𝜂̂/∂𝜂 𝛵˜𝑗0 + ∂𝑥̂𝑘/∂𝜂 𝛵˜𝑗𝑘)
= (1 - 𝛵)[(1 + 𝛵)𝛵˜00 + 𝐿𝑘ʹ 𝛵˜0𝑘] + (𝛿𝑖𝑗 - ∂𝑗𝐿𝑖)[(1 + 𝛵)𝛵˜𝑗0 + 𝐿𝑘ʹ𝛵˜𝑗𝑘] = -𝐿𝑖ʹ𝛵˜00 + 𝛵˜𝑖0 + 𝐿𝑗ʹ𝛵˜𝑗𝑗 + 𝛰(2)
= 𝐿𝑖ʹ𝜌̄ + 𝛵˜𝑖 0 + 𝐿𝑖ʹ𝑃̄ + 𝛰(2) = 𝛵˜𝑖 0 + (𝜌̄ + 𝑃̄)𝐿𝑖ʹ
Since 𝛵˜𝑖 0 = -𝑞̂𝑖 and 𝑞𝑖 = (𝜌̄ + 𝑃̄)𝑣𝑖,
(f) 𝑞𝑖 ↦ 𝑞𝑖 + (𝜌̄ + 𝑃̄)𝐿𝑖ʹ, 𝑣𝑖 ↦ 𝑣𝑖 + 𝐿𝑖ʹ. ▮
Gauge-invariant variables
We can define specific combinations of variables for which these transforms cancel. There are various gauge-invariant quantities that can be formed from the metric and matter variables.
• One useful combination is
(6.52) 𝜌̄∆ ≡ 𝛿𝜌 + 𝜌̄ʹ(𝑣 + 𝛣).
The quantity ∆ is called the comoving density contrast because it reduces to the density contrast in comving guage, 𝑣 = 𝛣 = 0. In terms of the comoving density contrast the relativistic generalization of Poisson equation takes the same form as in the Newtonian approximation
(6.53) ∇2𝛷 = 4π𝐺𝑎2 𝜌̄∆,
with 𝛷 is the Bardeen potential defined in (6.28).
• Two additional important gauge-invariant quantities are
(6.54-5) 𝛇 = -𝐶 + 1/3 ∇2𝐸 + 𝓗 𝛿𝜌/𝜌̄ʹ, 𝓡 = -𝐶 + 1/3 ∇2𝐸 - 𝓗(𝑣 + 𝛣).
These are called curvature perturbations because they reduce to the intrinsic curvature of spatial slices in uniform density and comoving gauge respectively.
Exercise 6.5 Consider the induced metric on surfaces of constant time
(6.56) 𝛾𝑖𝑗 = 𝑎2[(1 + 2𝐶)𝛿𝑖𝑗 + 2𝐸𝑖𝑗].
Show that the intrinsic curvature on the spatial slice is
(6.57) 𝑎2𝑅(3)[𝛾𝑖𝑗] = -4∇2𝐶 + 2∂𝑖∂𝑗𝐸𝑖𝑗 = 4∇2(-𝐶 + 1/3 ∇2𝐸).
This explains why -𝐶 + 1/3 ∇2𝐸 is called the "curvature perturbation."
[Solution] To get Ricci scalar of the spatial slice, 𝑅(3) we must find Christoffel symbol
(a) 𝛤𝑖𝑗𝑘 = 1/2 𝛾𝑖𝑙(∂𝑗𝛾𝑘𝑙 + ∂𝑘𝛾𝑗𝑙 - ∂𝑙𝛾𝑗𝑘),
Since at zeroth order 𝛾𝑖𝑗 = 𝑎-2𝛿𝑖𝑗 and we find the spatial derivatives
(b) 𝛤𝑖𝑗𝑘 = 𝛿𝑖𝑙∂𝑗(𝐶𝛿𝑘𝑙 + 𝐸𝑘𝑙) + 𝛿𝑖𝑙∂𝑘(𝐶𝛿𝑗𝑙 + 𝐸𝑗𝑙) - 𝛿𝑖𝑙∂𝑙(𝐶𝛿𝑗𝑘 + 𝐸𝑗𝑘) = (2𝛿𝑖(𝑗∂𝑘)𝐶 - 𝛿𝑗𝑘∂𝑖𝐶) + (2∂(𝑗𝐸𝑘))𝑖 - ∂𝑖𝐸𝑗𝑘).
(c) 𝑅(3) = 𝛾𝑖𝑘𝑅𝑖𝑘 = 𝛾𝑖𝑘(∂𝑙𝛤𝑙𝑖𝑘 - ∂𝑘𝛤𝑙𝑖𝑙 + 𝛤𝑙𝑖𝑘𝛤𝑚𝑙𝑚 - 𝛤𝑚𝑖𝑙𝛤𝑙𝑘𝑚),
This reduces to at first order
(d) 𝑎2𝑅(3) = 𝛿𝑖𝑘∂𝑙𝛤𝑙𝑖𝑘 - 𝛿𝑖𝑘∂𝑘𝛤𝑙𝑖𝑙.
(f) 𝛿𝑖𝑘∂𝑙𝛤𝑙𝑖𝑘 = 𝛿𝑖𝑘∂𝑙(2𝛿𝑖(𝑗∂𝑘)𝐶 - 𝛿𝑗𝑘∂𝑖𝐶) + 𝛿𝑖𝑘∂𝑙(2∂(𝑗𝐸𝑘))𝑖 - ∂𝑖𝐸𝑗𝑘) = -∇2𝐶 + 2∂𝑙∂𝑘𝐸𝑘𝑙
(g) 𝛿𝑖𝑘∂𝑘𝛤𝑙𝑖𝑙 = 3∇2𝐶
(h) 𝑎2𝑅(3) = -∇2𝐶 + 2∂𝑖∂𝑗𝐸𝑖𝑗 - 3∇2𝐶 = -4∇2𝐶 + 2∂𝑖∂𝑗𝐸𝑖𝑗.
Since only scalar perturbations contribute to ∂𝑖∂𝑗𝐸𝑖𝑗, [RE (6.4)] we get
(i) ∂𝑖∂𝑗𝐸𝑖𝑗 = ∂𝑖∂𝑗(∂𝑖∂𝑗𝐸 -1/3 𝛿𝑖𝑗∇2𝐸) = 2/3 ∇4𝐸.
Hence, we get
(j) 𝑎2𝑅(3) = 4∇2(-𝐶 + 1/3 ∇2𝐸). ▮
The three gauge-invariant perturbations ∆, 𝜁 and 𝘙 have the following relation
(6.58) 𝛇 = 𝓡 - 𝓗/𝜌̄ʹ 𝜌̄∆.
We see from the Poisson equation (6.53) that the comoving densiy contrast vanishes on superhorizon scales, so that the two curvature perturbations becomes equal
(6.59) 𝛇 →(𝑘 ≪ 𝓗)→ 𝓡.
On large scales we can therefore treat 𝜁 and 𝚁 interchangably. Since the curvature perturbations are constant on superhorizon scales if the matter perturbations are "adiabatic" (see Section 6.2.2), 𝛇 or 𝓡 is nice to describe the initial conditions.
More gauges
Above we used our gauge freedom to set the two of the metric perturbations to zero. Alternatively, we can also define the gauge in the matter sector:
• Uniform density gauge [Constant density gauge] We can use the freedom in the time slicing to set the total density perturbation to zero.
(6.60) 𝛿𝜌 = 0. [in summary: 𝛿𝜌 = 𝛣 = 0.]
The main scalar perturbation here is the curvature perturbation, 𝛿𝑔𝑖𝑗 = 𝑎2(1 - 2𝛇)𝛿𝑖𝑗.
• Comoving gauge Similarly, we can ask for the scalar momentum density to vanish,
(6.61) 𝑞 = 0. [in summary: 𝑣 = 𝛣 = 0.]
The main scalar perturbation here is the curvature perturbation, 𝛿𝑔𝑖𝑗 = 𝑎2(1 - 2𝓡)𝛿𝑖𝑗. This is another convenient gauge for the computation of the inflationary quantum fluctuations [5].
There are different versions of uniform density and comoving gauge depending on which of the metric fluctuation is set to zero.
|
|
|





































