|
김관석
|
2024-09-15 08:35:16, 조회수 : 485 |
- Download #1 : BC_3b.jpg (316.2 KB), Download : 0

3.1.4 Cosmic Neutrino Background
The most weekly interacting particles of the Standard Model are neutrinos. We therefore expect them to decouple first from the thermal plasma. How this produce the cosmic neutrino background (𝐶𝜈𝛣) will be shown in the following.
Neutrino decoupling
Neutrinos were coupled to the thermal bath through weak interaction process like
(3.57) 𝜈𝑒 + 𝜈̄𝑒 ⟷ 𝑒+ + 𝑒-, 𝑒- + 𝜈̄𝑒 ⟷ 𝑒- + 𝜈̄𝑒.
The interaction rate(/particle) is 𝛤 ≡ 𝑛𝜎∣𝑣∣, where 𝑛 is the number density of the target particles, 𝜎 is the cross section, and 𝑣 is the relative velocity (which is approximately 𝑣 ≈ 𝑐 = 1). By dimensional analysis, we infer that the cross section for weak scale interaction is 𝜎 ≈ 𝐺𝐹2𝛵2, where 𝐺𝐹 ≈ 1.2 × 10-5 GeV-2 is Fermi's constant. Taking the number density to be 𝑛 ≈ 𝛵3, the interaction rate becomes
(3.58) 𝛤 = 𝑛𝜎∣𝑣∣ ≈ 𝐺𝐹2𝛵5
As the temperature decrease, the interaction rate drops much more rapidly than the Hubble rate 𝐻 ≈ 𝛵2/𝑀𝑃𝐼:
(3.59) 𝛤/𝐻 ≈ (𝛵/1 MeV)3.
We conclude that neutrinos decouple around 1 MeV. (more accurately 0.8 MeV) After decoupling, the neutrinos more freely along geodesics and preserve the relativistic Fermi-Dirac distribution (even after they become non-relativistic at later time). In Section 2.2.1, we showed that the physical momentum of free-streaming particles scales as 𝑝 ∝𝑎-1. It's convenient to define the time-independent combination 𝑞 ≡ 𝑎𝑝, so that the neutrino number density is
(3.60) 𝑛𝜈 ∝𝑎3 ∫ 𝑑3𝑞 1/[exp(𝑞/𝑎𝛵𝜈) + 1].
After decoupling, particle number conservation requires 𝑛𝜈 ∝𝑎3, which is only consistent with (3.60) if the neutrino temperature evolves as 𝛵𝜈 ∝𝑎-1. As long as the photon temperature 𝛵𝛾 scales in the same way, we still have 𝛵𝜈 = 𝛵𝛾. However, particle annihilations will cause a deviation from 𝛵𝛾 ∝𝑎-1 in the photon temperature.
Electron-positron annihilation
Shortly after the neutrinos decouple, the temperature drops below the electron mass, so that electrons and positrons can annihilate into photons.
𝑒+ + 𝑒- → 𝛾 + 𝛾.
The energy density and entropy of electrons and positrons are transferred to the photons, but not to the decoupled neutrinos. The photons are thus "heated" (the photon temperature decreases more slowly) relative to the neutrinos (see Fig. 3.3). To quantify this effect, we consider the change in the effective number of degree of freedom in entropy. If we neglect neutrinos and other decoupled species,8 then we have
(3.61) 𝑔*𝑆 = { 2 + 7/8 × 4 = 11/2 𝛵 ≳ 𝑚𝑒; 2 𝛵 < 𝑚𝑒.
The annihilation of electrons and positrons occurs on a timescale of 𝛼2/𝑚𝑒 ~ 10-18 s (where 𝛼 is the fine-structure constant), which is much less than the age of the universe (~1 s) at the time. This means that the 𝑒±-𝛾 plasma evolves quasi-adiabatically into the 𝛾-only plasma. Entropy is therefore conserved during the process. Taking 𝑔*𝑆(𝑎𝛵𝛾)3 to remain constant, we find that 𝑎𝛵𝛾 increases after electron-positron annihilation by a factor (11/4)1/3, while 𝑎𝛵𝜈 remains the same. This means that after 𝑒+𝑒- annihilation, the neutrino temperature is slightly lower than the photon temperature.
(3.62) 𝛵𝜈 = (4/11)1/3 𝛵𝛾. [𝛵𝜈≈ 0.714 𝛵𝛾]
For 𝛵 ≪ 𝑚𝑒, the effective number of relativistic species (in energy density and entropy) therefore is
(3.63) 𝑔* = 2 + 7/8 × 2 𝑁eff (4/11)4/3 = 3.36,
(3.64) 𝑔*𝑆 = 2 + 7/8 × 2 𝑁eff (4/11) = 3.94,
where 𝑁eff is the effective number of neutrino species in the universe. If neutrino decoupling was instantaneous then we would simply have 𝑁eff = 3. However, neutrino decoupling was not quite complete when 𝑒+𝑒- annihilation began, so some of the energy and entropy did leak to neutrinos. Taking this into account9 raises the effective number of neutrinos to 𝑁eff = 3.046.10 Using this value in (3.63) explains the final value of 𝑔*(𝛵) in Fig. 3.2.
Electron-positron annihilation
The relation (3.62) holds until the present. The cosmic neutrino background therefore has a slightly lower temperature 𝛵𝜈,0 = 1.95 K. cf. CMB 𝛵𝜈0 = 2.73 K. The number density of neutrinos (per flavor) is
(3.65) 𝑛𝜈 ≈ 3/4 × 4/11 𝑛𝛾.
Using (3.24) we see that this corresponds to 112 neutrinos cm per flavor. The present energy density of neutrinos depends on whether the neutrinos are relativistic or non-relativistic today. It used to be believed that neutrinos were massless, in that case
(3.66) 𝜌𝜈 = 7/8 𝑁eff (4/11)4/3𝜌𝛾 ⇒ 𝛺𝜈𝘩2 ≈ 1.7 × 10-5 (𝑚𝜈 = 0). [𝘩 = 𝐻0/100 Mpc km s-1]
However, neutrino oscillation experiments have shown that neutrinos do have a mass. The minimum sum of the neutrino masses is ∑ 𝑚𝜈,𝑖 > 0.06 eV. massive neutrinos behave as radiation-like particles in the early universe (for 𝑚𝜈 < 0.2 eV, neutrinos are relativistic at recombination) and as matter-like particles in the late universe (see Fig. 3.4). In Problem 3.4, it will be shown that energy of massive neutrino, 𝜌𝜈 = ∑ 𝑚𝜈,𝑖𝑛𝜈,𝑖, corresponds to
(3.67) 𝛺𝜈𝘩2 ≈ ∑ 𝑚𝜈,𝑖/(94 eV). [𝘩 = 𝐻0/100 Mpc km s-1]
By demanding that 𝛺𝜈 <1, a cosmological upper bound can be placed on the sum of the neutrino masses ∑ 𝑚𝜈,𝑖 < 15 eV (using 𝘩 ≈ 0.7). Massive neutrinos also affect the late-time expansion rate which is constraint by CBM and BAO(Baryon acoustic oscillations) measurements. The current Planck constraint is ∑ 𝑚𝜈,𝑖 < 0.13eV, which implies 𝛺𝜈 < 0.003. Future observations promise to be sensitive enough to measure the neutrino masses.
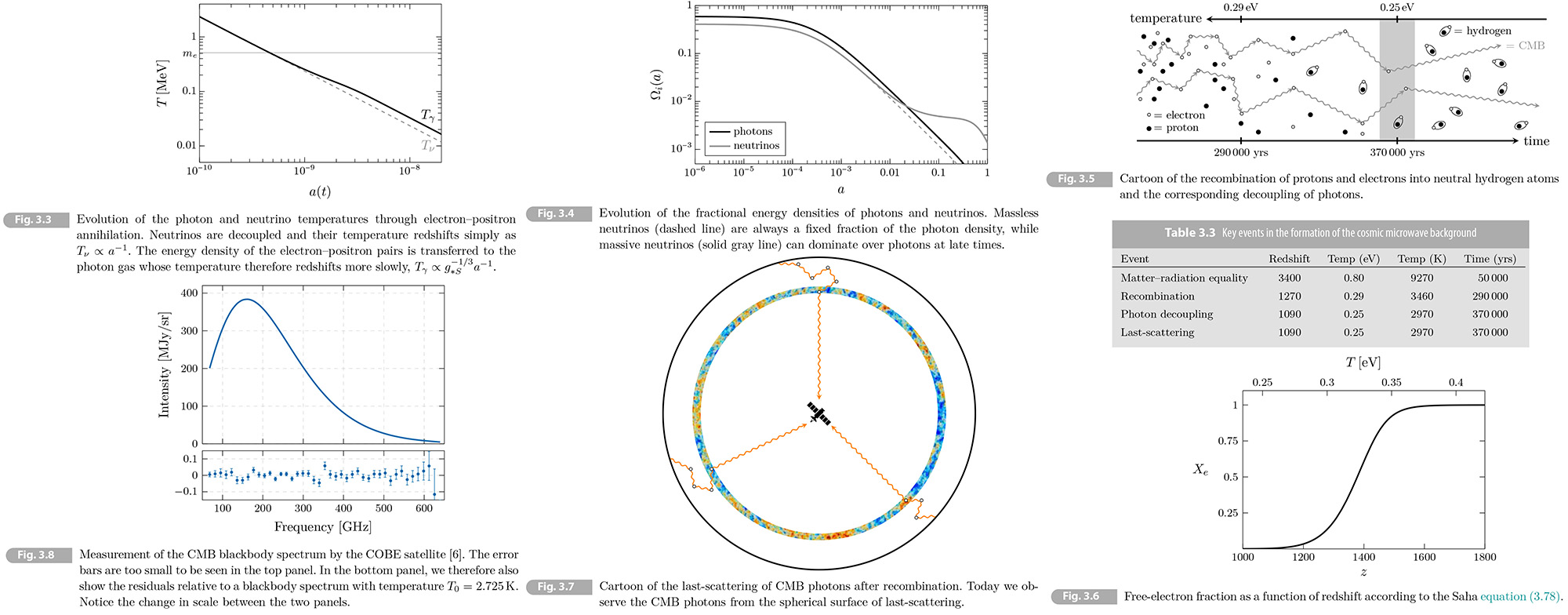
3.1.5 Cosmic Microwave Background
An important event in the history of the early universe is the formation of the first atoms and the associated decoupling of photons. (see Fig. 3.5). At temperatures above about 1eV this universe still consisted of a plasma of free electrons and nuclei. Photons were tightly coupled to the electrons via Thomson
scattering, which in tern strongly interacted with protons via Coulomb scattering. There was very little neutral hydrogen. Below 0.3 eV the electons and nuclei combined to form neutral atoms and the density of free electrons decreased sharply. The photon mean free path grew rapidly and became longer than the Hubble length, 𝐻-1. Around 0.25 eV, the photons decoupled from the matter and the universe became transparent. Today, these photons are observed as the cosmic microwave background. Key events in the formation of the CMB are summarized in Table 3.3. We will derive these facts.
Chemical equilibrium
During the recombination, the number of each particle species wasn't fixed, because hydrogen atoms were formed, while the number of free electrons and protons decreased. In thermodynamics we describe such a situation with chemical potential.
Consider the generic reaction
1 + 2 ⟷ 3 + 4.
Each particle species has a chemical potential 𝜇. The second law of thermodynamics implies that particles flow to the side of the reaction where the total chemical potential is lower. Chemical equilibrium is reached when the sum of the chemical potentials each side is equal, in which case the rates of the forward and revers reaction are equal. So
(3.68) 𝜇1 + 𝜇2 = 𝜇3 + 𝜇4.
• There is no chemical potential for photons, because photon number is not conserved. (e.g. double Compton scattering 𝑒- + 𝛾 ⟷ 𝑒- + 𝛾 + 𝛾 happens in equilibrium at high temperatures.) Sometimes, this is expressed as
(3.69) 𝜇𝛾 = 0,
but, more accurately the concept of a chemical potential for photons doesn't exist.
• If the chemical potential of a particle 𝑋 is 𝜇𝑥, then the chemical potential of the corresponding antiparticle 𝑋̄ is
(3.70) 𝜇𝑥̄ = -𝜇𝑥.
To see this, just consider particle-antiparticle annihilation, 𝑋 + 𝑋̄ ⟷ 𝛾 + 𝛾, and use that 𝜇𝛾 = 0,
The equilibrium assumption will be sufficient to describe the onset of recombination, but will not capture the correct dynamics shortly thereafter (such as the freeze-out of electrons). We will revisit these non-equilibrium aspects of recombination in Section 3.2.5.
Hydrogen recombination
Recombination proceeds in two stages. The formation of helium atoms is followed by that of hydrogen atoms. We will assume that the universe was filled only with free electrons, protons and photons. Over 90% (by number) of the nuclei are protons, so this is reasonable approximation to reality. Moreover , helium recombination is completed before hydrogen recombination, so hat the two events can be treated separately.
The formation of hydrogen atom occurs via the reaction
𝑒- + 𝑝+ = 𝐻 + 𝛾,
Initially, this reaction keeps the particles in equilibrium, and since 𝛵 < 𝑚𝑖, 𝑖 = {𝑒, 𝑝, 𝐻}, we have the following equilibrium abundances
(3.71) 𝑛𝑖eq = 𝑔𝑖 (𝑚𝑖𝛵/2π)3/2 exp[(𝜇𝑖 - 𝑚𝑖)/𝛵],
where 𝜇𝑝 + 𝜇𝑒 = 𝜇𝐻 (recall that 𝜇𝛾 = 0). To remove ththe following ratioe dependence on the chemical potentials, we consider
(3.72) (𝑛𝐻/𝑛𝑒𝑛𝑝)eq = 𝑔𝐻/𝑔𝑒𝑔𝑝 (𝑚𝐻/𝑚𝑒𝑚𝑝 2π/𝛵)3/2 𝑒(𝑚𝑝 + 𝑚𝑒 - 𝑚𝐻)/𝛵.
In the prefactor, we can use 𝑚𝐻 ≈ 𝑚𝑝, but in the exponential the small difference is crucial: it is the ionization energy of hydrogen
(3.73) 𝐸𝐼 ≡ 𝑚𝑝 + 𝑚𝑒 - 𝑚𝐻 = 13.6 eV.
The numbers of internal degrees of freedom are 𝑔𝑝 = 𝑔𝑒 =2 and 𝑔𝐻 =4.11 In our knowledge the universe isn't electrically charged, so that we have 𝑛𝑒 = 𝑛𝑝, Equation (3.72) then becomes
(3.74) (𝑛𝐻/𝑛𝑒2)eq = (2π/𝑚𝑒𝛵)3/2 𝑒𝐸𝐼/𝛵.
It is convenient to describe the process of recombination in terms of the free electron fraction
(3.75) 𝑋𝑒 ≡ 𝑛𝑒/(𝑛𝑝 + 𝑛𝐻) = 𝑛𝑒/(𝑛𝑒 + 𝑛𝐻).
A fully ionized universe corresponds 𝑋𝑒 = 1, while a universe of only neutral atoms has 𝑋𝑒 = 0. Our goal is to understand how 𝑋𝑒 evolves. If we neglect the small number of helium atoms, then the denominator in (3.75) can be approximated by the baryon density
(3.76) 𝑛𝑏 = 𝜂 𝑛𝛾 = 𝜂 × 2𝜁(3)/π2 𝛵3, [RE (3.24) 𝑛𝛾,0 = 2𝜁(3)/π2 𝛵03]
where 𝜂 is the baryon-to-photon ratio. We can then write
(3.77) (1 - 𝑋𝑒)/𝑋𝑒2 = 𝑛𝐻/𝑛𝑒2 𝑛𝑏,
and substituting (3.74), we arrive at the so-called Saha equation
(3.78) [(1 - 𝑋𝑒)/𝑋𝑒2]eq = 2𝜁(3)/π2 𝜂 (2π𝛵/𝑚𝑒)3/2 𝑒𝐸𝐼/𝛵
The solution to this equation is
(3.79) 𝑋𝑒 = [-1 ± √(1 + 4𝑓)]/2𝑓,* with 𝑓(𝛵,𝜂) = 2𝜁(3)/π2 𝜂 (2π𝛵/𝑚𝑒)3/2 𝑒𝐸𝐼/𝛵, *[correcton: from [-1 + √(1 + 4𝑓)]/2𝑓 to [-1 ± √(1 + 4𝑓)]/2𝑓]]
which is shown in Fig. 3.6 as a function of temperature (or equivalently redshift).
Let us define the recombination temperature 𝛵rec the temperature at which as 𝑋𝑒 = 0/5 in (3.78).12 For 𝜂 ≈ 6 × 10-10, we get
(3.80) 𝛵rec ≈ 0.32 eV ≈ 3760 K.
The reason why the recombination temperature is significantly below the binding energy of hydrogen, 𝛵rec ≪ 𝐸𝐼 = 13.6 eV, is that there are many photons for each hydrogen atom. Even when 𝛵 < 𝐸𝐼, the high-energy tail of the
𝐸𝐼, the high-energy tail of the photon distribution contains photons with energy 𝐸𝛾 > 𝐸𝐼, which can ionize the hydrogen atoms. Concretely, although the mean photon energy is <𝐸𝛾> ≈ 2.7 𝛵, one in 500 photons has 𝐸𝛾 > 10 𝛵, one in 3 × 106 has 𝐸𝛾 > 20 𝛵, and one in 3 × 1010 has 𝐸𝛾 > 30 𝛵. Since there are over 109 photons per baryon, rare high-energy photons are still present in sufficient numbers, unless the temperature drops far below the binding energy.
𝛵rec = 𝛵0(1 + 𝑧rec), with 𝛵0 =2.73 K, gives 𝑧rec ≈ 1380.13. However, we will see in Section 3.2.5 that the details of recombination are more complex and is delayed relative to the Saha prediction, with 𝑋𝑒 = 0.5 only being reached at
(3.81) 𝑧rec ≈ 1270, 𝑡rec ≈ 290 000 yrs.
Since matter-radiation equality is at 𝑧rec ≈ 3400, we conclude that recombination occurred in matter-dominated era. Of course, it was not an instantaneous process as seen from Fig. 3.6. It took about 𝛥𝑡 ≈ 70 000 yrs (or 𝛥𝑧 ≈ 180*) for the ionization fraction to drop from 𝑋𝑒 = 0.9 to 𝑋𝑒 = 0.1. *[correction: from ∆𝑧 ≈ 80 to ∆𝑧 ≈ 180]
Photon decoupling
At early times, photons are strongly coupled to the primordial plasma through their interaction with the free electrons
𝑒- + 𝛾 ⟷ 𝑒- + 𝛾,
with the interaction rate given by 𝛤𝛾 ≈ 𝑛𝑒 𝜎𝛵 ≈ 2 × 10-3 MeV-2 is the Thomson cross section. At 𝑎 = 10-5 (prior to matter-radiation equality), the rate of photon scattering is 𝛤𝛾 ≈ 5.0 × 10-6 s-1, or three times per week. This interaction rate was much larger than the expansion rate at that time (𝐻 ≈ 2 × 10-10 s-1), so thah electrons and photons were in equilibrium.
Since 𝛤𝛾 ∝ 𝑛𝑒, the interaction rate decrease as the density of free electrons drops during recombination. At some point, this rate becomes smaller than the expansion rate and photons decouple. We define the approximate moment of photon decoupling as 𝛤𝛾(𝛵dec) ≈ 𝐻(𝛵dec).
(3.82) 𝛤𝛾(𝛵dec) = 𝑛𝑏 𝑋𝑒(𝛵dec) 𝜎𝛵 = 2𝜁(3)/π2 𝜂 𝑋𝑒(𝛵dec) 𝛵dec3,
(3.83) 𝐻(𝛵dec) = 𝐻0 √𝛺𝑚 (𝛵dec/𝛵0)3/2, we get
(3.84) 𝑋𝑒(𝛵dec) 𝛵dec3/2 ≈ π2/2𝜁(3) 𝐻0√𝛺𝑚/𝑛𝜎𝛵𝛵03/2.
Using the Saha equation for 𝑋𝑒(𝛵dec) we find 𝛵dec ≈ 0.27 eV. In the more precise treatment in Section 3.2.5, we find that decoupling occurs at a slightly lower temperature,
(3.85-86) 𝛵dec ≈ 0.25 eV ≈ 2970 K, 𝑧rec ≈ 1090, 𝑡rec ≈ 370 000 yrs.
After decoupling, the photons stream freely through the universe.
Note that the ionization fraction decreases significantly between recombination and decoupling. 𝑋𝑒(𝛵rec) ≈ 5 → 𝑋𝑒(𝛵dec) ≈ 0.001. This show that a large degree of neutrality is necessary before the universe becomes transparent to photons.
Exercise 3.4 Imagine that he recombination did not occurs, so that 𝑋𝑒 = 1. At what redshift would the CMB photons now decouple?
[Solution] From definition of photon decoupling, 𝛤𝛾(𝛵dec) ≈ 𝐻(𝛵dec), so we have (3.84)
(a) 𝑋𝑒(𝛵dec) 𝛵dec3/2 ≈ π2/2𝜁(3) 𝐻0√𝛺𝑚/𝑛𝜎𝛵𝛵03/2. and 𝑋𝑒 ≡ 1
(b) 𝛵dec = [π2/2𝜁(3) 𝐻0√𝛺𝑚/𝑛𝜎𝛵𝛵03/2]2/3
To evaluate this we first write all quantities in natural units, using
(c) 𝑐 = 3 × 108 m s-1 ≡ 1, ℏ𝑐 = 2 × 10-7 eV m ≡ 1
For we use 𝐻0 ≈ 70 km s-1 Mpc-1 = 70/3 × 105 (3.1 × 1022 m)-1 = 70/3 × 105 2 × 10-7/3.1 × 1022 eV = 1.5 × 10-33 eV
The photon temperature today is 𝛵0 ≈ 2.725 K or 2.348 × 10-4 eV.
The Thomson cross section [RE Wikipedia Thomson scattering: For an electron ...] 𝜎𝛵 = 6.65 × 10-29 m2 = 6.65 × 10-29/(2 × 10-7)2 eV-2 = 1.66 × 10-15 eV-2
Substituting these results, π2/2𝜁(3) ≈ 4.105 and 𝛺𝑚 = 0.315 [RE Wikipedia Lambda-CDM model] into the equation gives
(d) 𝛵dec ≈ [4.105 × (1.5 × 10-33 × √0.315)/{6 × 10-10 × (1.66 × 10-15) × (2.3 × 10-4)3/2}]2/3 eV ≈ 9.76 × 10-3 eV.
The redshift of decoupling is, using 𝛵dec = 𝛵0(1 + 𝑧dec), [Wikipedia Cosmic micro background: 𝛵r = 2.725 K × (1 + 𝑧)]
(e) 𝑧dec = 𝛵dec/𝛵0 - 1 = 9.76/0.23 - 1 ≈ 41. ▮
Last-scattering
The scattering of photons off electrons essentially stops at photon decoupling. To define the precise moment of last-scattering, we have to consider the probability of photon scattering. Let 𝑑𝑡 b a small time interval around the time 𝑡. The probability that a photon will scatter during this time is 𝛤𝛾(𝑡) 𝑑𝑡, and the integrated probability between the time 𝑡 and 𝑡0 > 𝑡 is
(3.91) 𝛤𝛾(𝑡) = ∫𝑡𝑡0 𝛤𝛾(𝑡) 𝑑𝑡,
This probability is also called the optical depth. Taking 𝑡0 to be the present time, the moment of lat-scattering is defined by 𝜏(𝑡*) ≡ 1. To a good approximation, last scattering coincides with photon decoupling, 𝑡* ≈ 𝑡dec. However, the optical dept is sensitive to the evolution of free electron density at the end of recombination, which isn't captured well by the equilibrium treatment of this section. A precise evaluation of 𝑡* must therefore await our non-equilibrium analysis of recombination in Section 3.2.5.
When we observe the CMB, we are detecting photons from this surface of last-scattering (see Fig. 3.7). Given the age of the universe, and taking into account the expansion of the universe, the distance us and the spherical last-scattering surface today is 42 billion light-years. Of course, last-scattering is a probabilistic concept-not all photons experienced their last scattering event at the same time-so there is some thickness to the last-scattering surface.
Blackbody spectrum
The CBM is often presented as key evidence that the early universe began in a state of thermal equilibrium. Before decoupling, the number density of photons with frequency in the range 𝑓 and 𝑓 + 𝑑𝑓 is
(3.88) 𝑛(𝑓,𝛵) 𝑑𝑓 = 2/𝑐3 4π𝑓2/(𝑒𝘩𝑓/𝑘𝛣𝛵 - 1) 𝑑𝑓,
where factors of 𝑐 and 𝑘𝛣 were restored for clarity. This frequency distribution is called the blackbody spectrum and is characteristic of objects in thermal equilibrium.After decoupling, the photons propagate freely, with their frequencies redshifting as 𝑓(𝑡) ∝𝑎(𝑡)-1 and number density decreasing as 𝑎(𝑡)-3. The spectrum therefore maintains is blackbody form as long as we take the temperature to such scale as 𝛵 ∝ 𝑎(𝑡)-1. Te early e relic radiation encodes the early equilibrium phase of the hot Big Bang.
CMB experiments observe the so-called spectral radiation intensity, 𝐼𝑓, which is the flux of energy per unit area per unit frequency. Let us see how this is related to the spectrum in (3.68). We first pick a specific direction and consider photons traveling in a solid angle 𝛿𝛺 around the this direction. In a given time interval 𝛿𝑡, these photons move through a volume 𝛿𝑉 = (𝑐𝛿𝑡)3 𝛿𝛺 and cross a cap of area 𝛿𝛢 = (𝑐𝛿𝑡)2 𝛿𝛺. The number of photons in this volume is
(3.89) 𝛿𝑁 = 𝑛(𝑓)𝑑𝑓/4π 𝛿𝑉 = 2/𝑐3 𝑓2𝑑𝑓/(𝑒𝘩𝑓/𝑘𝛣𝛵 - 1) (𝑐𝛿𝑡)3 𝛿𝛺,
and the number of photons crossing the surface per unit area and per unit time is
(3.90) 𝛿𝑁/𝛿𝛢𝛿𝑡 = 2/𝑐2 𝑓2𝑑𝑓/(𝑒𝘩𝑓/𝑘𝛣𝛵 - 1).
Since each photon has energy 𝘩𝑓, the flux of energy across the surface (per unit frequency) is
(3.91) 𝐼𝑓 = 2𝘩/𝑐2 𝑓3/(𝑒𝘩𝑓/𝑘𝛣𝛵 - 1).
Figure 3.8 shows a measurement of the CMB frequency spectrum by the FIRAS instrument on the COBE satellite. What you are seeing is the most perfect blackbody ever observed in nature, proving that the early universe indeed started in a state of thermal equilibrium.
8 Obviously entropy is separately conserved for the thermal bath and the decoupled species.
9 For the precise value, we should consider that the neutrino spectrum after decoupling deviates slightly from the Fermi-Dirac distribution. The spectral distortion arise because the energy dependence of the weak interaction causes neutrinos in the high-energy tail to interact more strongly.
10 But the Planck constraint on 𝑁eff = 2.99 ± 0.17 (≠ 3.046), so this leaves room for discovering new physics beyond the Standard Model.
11 The spins of the electron and proton in a hydrogen atom can be aligned or anti-aligned, giving one singlet state and one triplet state, so 𝑔𝐻 = 1 + 3 = 4.
12 the choice of 𝑋𝑒 = 0/5 looks like arbitrary. However, since 𝑋𝑒 is exponentially sensitive to 𝛵, we don't change this criterion.
13 It's useful to compare this to the case of helium recombination. This proceed in two stage: First, He2+ captures one 𝑒- to create He+. This process occurs in equilibrium around 𝑧 ≈ 6000. Then He+ captures a second 𝑒- to become a neural helium He. This is slower than predicted by Saha equilibrium and occurs around 𝑧 ≈ 2000. This means that helium recombination don't have a big effect on he hydrogen recombination and the predictions of CMB, since the universe was still optically thick after the completion of the helium recombination.
Problem 3.4 Massive neutrinos
At least two of the three neutrino species in the Standard Model must have small masses. We will explore the cosmological consequences of this neutrino mass.
1. Let us assume that the neutrino mass is small enough, so that the neutrinos are relativistic at decoupling. Show that the energy density after decoupling is
(a) 𝜌𝜈 = 𝛵𝜈4/π2 ∫0∞ 𝑑𝜉 𝜉2 √(𝜉2 + 𝑚𝜈2/𝛵𝜈2)/(𝑒𝜉 + 1),
where 𝛵𝜈 is the neutrino temperature.
[Solution] Since the neutrinos are relativistic when they decouple and The contribution of a neutrino flavor with mass 𝑚𝜈 to the energy density is
(b) 𝜌𝜈 = 𝑔/(2π)3 ∫ 𝑑3𝑝 𝑓(𝑝,𝛵) 𝐸(𝑝), 𝑔𝜈 = 2; 𝜌𝜈 = 2/2π2 ∫0∞ 𝑑𝑝 𝑝2√(𝑝2 + 𝑚2)/[𝑒{√(𝑝2 + 𝑚2)/𝛵} ± 1]. + sign for fermion, 𝑚𝜈2/𝛵𝜈 ≈ 0;
(c) 𝜌𝜈 = 1/π2 ∫0∞ 𝑑𝑝 𝑝2√(𝑝2 + 𝑚2)/𝑒𝑝/𝛵𝜈 + 1]. 𝜉 ≡ 𝑝/𝛵𝜈; 𝜌𝜈 = 1/π2 ∫0∞ 𝑑(𝜉𝛵𝜈) (𝜉𝛵𝜈)2√[(𝜉𝛵𝜈)2 + 𝑚2]/(𝑒𝜉 + 1) ⇒
(d) 𝜌𝜈 = 𝛵𝜈4/π2 ∫0∞ 𝑑𝜉 𝜉2 √(𝜉2 + 𝑚𝜈2/𝛵𝜈2)/(𝑒𝜉 + 1). ▮
2. By considering a series expansion for small 𝑚𝜈/𝛵𝜈 show that
(e) 𝜌𝜈 ≈ 𝜌𝜈0 (1 + 5/7π2 𝑚𝜈2/𝛵𝜈2),
where 𝜌𝜈0 is the energy density of massless neutrinos.
[Solution] For a massless neutrinos, the energy density formula derived above with 𝑚𝜈 = 0,
(f) 𝜌𝜈0 = 𝛵𝜈4/π2 ∫0∞ 𝑑𝜉 𝜉3/(𝑒𝜉 + 1) = 𝛵𝜈4/π2 7π4/120 = 7π2/120 𝛵𝜈4.
Since 𝑚𝜈/𝛵𝜈 is small and using Taylor expansion √(𝜉2 + 𝑚𝜈2/𝛵𝜈2) ≈ 𝜉 + 1/2𝜉 (𝑚𝜈/𝛵𝜈)2
(g) 𝜌𝜈 ≈ 𝛵𝜈4/π2 ∫0∞ 𝑑𝜉 𝜉2/(𝑒𝜉 + 1) [𝜉 + 1/2𝜉 (𝑚𝜈/𝛵𝜈)2] = 𝜌𝜈0 + 𝛵𝜈2𝑚𝜈2/2π2 ∫0∞ 𝑑𝜉 𝜉/(𝑒𝜉 + 1) = 𝜌𝜈0 + 𝛵𝜈2𝑚𝜈2/2π2 π2/12,
(h) 𝜌𝜈 ≈ 𝜌𝜈0 + 𝛵𝜈2𝑚𝜈2/24 = 𝜌𝜈0(1 + 5/7π2 𝑚𝜈2/𝛵𝜈2). ▮
3. If 𝜌𝜈 is significantly larger than 𝜌𝜈0 at recombination, then the mass of the neutrinos affects the CMB anisotropies. What is the smallest neutrino mass that is observable in the CMB?
[Solution] This implies that 5/7π2 𝑚𝜈2/𝛵𝜈2 > 0, so
(i) 𝑚𝜈 > √(7π2/5) 𝛵𝜈,rec = √(7π2/5) (4/11)21/3 𝛵𝛾,rec
where we have used the relation between neutrino and photon temperatures after electron-positron annihilation. 𝛵𝛾,rec ≈ 0.32 eV, so
(j) 𝑚𝜈 > √(7π2/5) (4/11)21/3 × 0.32 eV ≈ 0.85 eV. ▮
If the neutrino mass is larger than the present photon temperature 𝛵𝛾,0 ≈ 0.235 meV, then these neutrinos will be non-relativistic today.
4. Estimate the redshift at which the neutrinos become non-relativistic.
[Solution] Neutrinos become non-relativistic when their temperature falls below their mass at 𝛵𝜈,n-r ~ 𝑚𝜈. Recall that after decoupling theit temperature evolves 𝛵𝜈 ∝ 𝑎-1 and 1 + 𝑧 = 𝑎-1, so
(k) 𝛵𝜈,n-r/𝛵𝜈,0 = 1 + 𝑧n-r ⇒ 𝑧n-r = 𝛵𝜈,n-r/𝛵𝜈,0 - 1 ≈ 𝛵𝜈,n-r/1.95 K - 1 ≈ 𝑚𝜈/(4/11)1/3𝛵𝛾,0 ≈ (𝑚𝜈/0.714 × 0.2348 meV) -1 ≈ (𝑚𝜈/0.17 meV) -1. ▮
5. Compute the number density of these neutrinos today.
[Solution] When the neutrinos decoupled, they were in relativistic limit, so we can use equation 𝑛 = 3/4 𝜁(3)/π2 𝑔 𝛵3 (for femion), therefore
(l) 𝑛𝜈 = 3𝜁(3)/4π2 𝑔𝜈 𝛵dec3.
Since neutrinos are decoupled and temperature redshifts simply as 𝛵𝜈 ∝ 𝑎-1 (see Fig. 3.3), so we can write
(m) 𝑛𝜈,0 = 3𝜁(3)/4π2 𝑔𝜈 𝛵𝜈,03,
where we allow the neutrinos to evolve on geodesics. However, we have the photon number density today which is given by relativistic thermodynamics
(n) 𝑛𝛾,0 = 𝜁(3)/π2 𝑔𝛾 𝛵𝛾,03,
Now we can compute the ratio of the two number density using 𝛵𝜈 = (4/11)1/3 𝛵𝛾,
(o) 𝑛𝜈,0/𝑛𝛾,0 = 3/4 𝑔𝜈/𝑔𝛾 (𝛵𝜈,0/𝛵𝛾,0)3 = 3/4 × 2/2 × 4/11 = 3/11. ▮
6. Show that their contribution to the energy density in the universe today is
(p) 𝛺𝜈𝘩2 ≈ 𝑚𝜈/94 EV.
Use the lower bound on the sum of the neutrino masses from oscillation experiments, ∑ 𝑚𝜈 > 0.06 eV, to derive bound on the total neutrino density. How does this compare to the cosmological bound 𝛺𝜈𝘩2 < 0.001 ?
[Solution] Since the neutrinos are non-relativistic today, their energy density is the same as their mass density, so
(q) 𝜌𝜈,0 = 𝑚𝜈𝑛𝜈,0 = 3/11 𝑚𝜈𝑛𝛾,0.
The fractional energy in such a neutrino is, using 𝛵𝛾,0 ≈ 0.2348 meV and 𝛺𝛾,0𝘩2 ≈ 2.47 × 10-5,
(r) 𝛺𝜈𝘩2 = 𝜌𝜈,0/𝜌𝛾,0 𝛺𝛾𝘩2 = 3/11 𝑚𝜈𝑛𝛾,0/𝜌𝛾,0 = 3/11 𝑚𝜈 (2𝜁(3)/π2 𝛵𝛾,03)/(π2/15 𝛵𝛾,04) = 90𝜁(3)/11π2 𝑚𝜈/0.2348 meV 2.47 × 10-5 ≈ 𝑚𝜈/94eV. ▮
If ∑ 𝑚𝜈 > 0.06 eV, we get 𝛺𝜈𝘩2 > 0.0006, which is not far from the cosmological upper bound, 𝛺𝜈𝘩2 < 0.001. ▮
7. Discuss qualitatively why a much larger mass would still be compatible with the standard cosmology.
[Solution] If 𝑚𝜈 ≫ 𝛵dec, then the neutrinos were already non-relativistic at decoupling. As we can see in Fig. 3.4, at late time the energy density of massive neutrinos start to dominate over photons. Now we can measure the matter density of neutrinos without any constraint. ▮ |
|
|





































