|
김관석
|
2024-10-27 15:46:14, 조회수 : 100 |
- Download #1 : BC_6c.jpg (528.4 KB), Download : 0

6.3 Growth of Matter Perturbations
An important scale in structure formation is the horizon at matter-radian equality. A mode entering the horizon at the time of euality has wavenumber 𝑘eq = 𝓗eq. Mode with 𝑘 > 𝑘eq enter horizon during the radiation era, while modes with 𝑘 < 𝑘eq enter during the matter era. This leads to a scale -dependent evolution of matter perturbation. We will noe derive this evolution again connecting it more rigorously to the superhorizon limit of fluctuations.
6.3.1 Evolution of the Potential
Let us begin with the evolution of the gravitational potential. We will neglect anisotropic stress and assume adiabatic perturbations. Analytic solutions for 𝛷 can be found when the modes are on superhorizon scales, or when either radiation or matter dominate the background (see Fig. 6.4).
When the universe is dominated by a component with a constant equation of state, evolution equation is (see Exercise 6.11)
(6.159) 𝛷ʺ + 3(1 + 𝜔)𝓗𝛷ʹ - 𝜔∇2𝛷 = 0.
During the matter domination, we have 𝜔 ≈ 0 and (6.159) takes the same form on subhorizon scales as well as superhorizon scales. The solutions for the growing and decaying modes are
(6.160) 𝛷(𝑎, 𝐤) = 𝐶1(𝐤) + 𝐶2(𝐤)𝑎-5/2 (matter era),
[Derivation (2.149) 𝑎 ∝𝜂2. ⇒ 𝓗 = 𝑎ʹ/𝑎 = (𝜂2)ʹ/𝜂2 = 2/𝜂. ⇒ 𝛷ʺ + 6/𝜂 𝛷ʹ = 0. ⇒ 𝛷 = 𝐶1 + 𝐶2𝜂-5 = 𝐶1 + 𝐶2𝑎-5/2. ▮]
where we used 𝑎 ∝ 𝜂2 to write the decaying mode in terms of the scale factor. The amplitude 𝐶1(𝐤) and 𝐶1(𝐤) are determined by the initial conditions and the evolution during the radiation era. We see that growing modes of the gravitational potential is a constant on all scales during the matter era.
During the radiation era, we have 𝜔 ≈ 1/3, we find Fourier mode now satisfies
(6.161) 𝛷ʺ + 4/𝜂 𝛷ʹ + 1/3 𝑘2𝛷 = 0. [RE (5.14) ∇2 = -𝑘2 in Fourier mode]
writing 𝛷 = 𝑢(𝜑)/𝜑, with 𝜑 = 𝑘𝜂/√3, we have
(6.162) 𝑑2𝑢/𝑑𝜑2 + 2/𝜑 𝑑𝑢/𝑑𝜑 + (1 - 2/𝜑2)𝑢 = 0. [verification needed]
The solutions of this equation are the spherical Bessel functions (see Appendix D)
(6.163) 𝑗1(𝜑) = + sin(𝜑)/𝜑2 - cos(𝜑)/𝜑 = + 𝜑/3 + O(𝜑3),
(6.164) 𝑛1(𝜑) = + cos(𝜑)/𝜑2 - sin(𝜑)/𝜑 = - 𝜑/𝜑2 + O(𝜑0),
Since 𝑛1(𝜑) blows up for small 𝜑 (early times), we reject that solution on the basis of initial conditions. The solution for the gravitational potential during the radiation era then is
(6.165) 𝛷(𝜂, 𝐤) = 2𝓡𝑖 [sin(𝜑) - 𝜑 cos(𝜑)]/𝜑3 (radiation era),
where the overall normalization was determined by 𝛷(0, 𝐤) = 2/3 𝓡(0, 𝐤) ≡ 2/3 𝓡𝑖(𝐤) [RE Exercise 6.13]. Notice that (6.165) is valid on all scales. Taking the limits 𝜑 ≪ 1 and 𝜑 ≫ 1 on superhorizon and subhorizon scales respectively. These are
(6.166) 𝛷(𝜂, 𝐤) ≈ { 2/3 𝓡𝑖 (superhorizon); -6𝓡𝑖 cos(1/√3 𝑘𝜂)/(𝑘𝜂)2 (subhorizon). [verification needed]
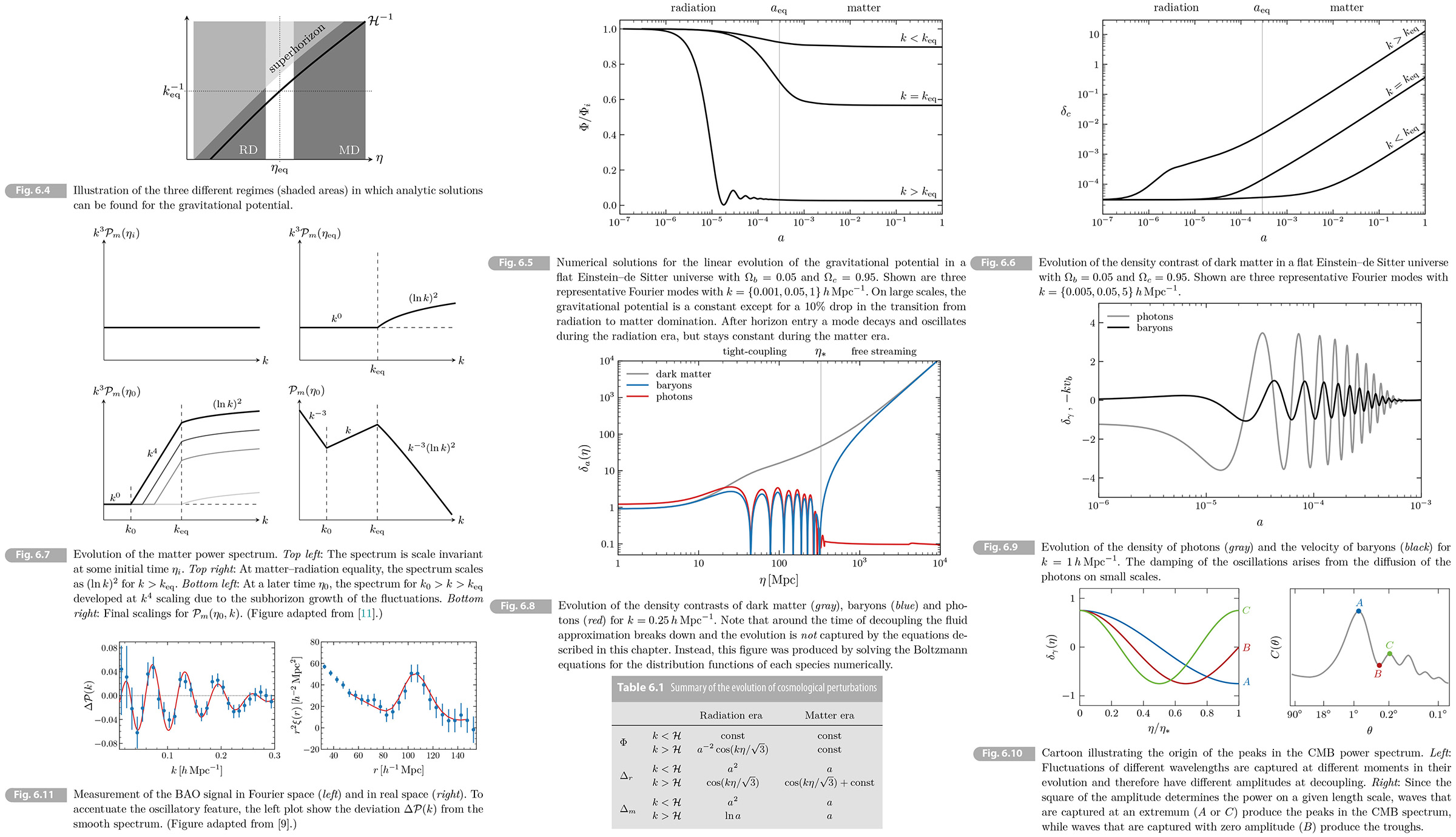
During the radiation era, subhorizon modes of 𝛷 therefore oscillate with a frequency 1/√3 𝑘 and have an amplitude that decays as 𝜂-2 ∝ 𝑎-2.
Fig. 6.5 shows numerical solutions for the evolution of the gravitational potential for 3 representative wavelengths. As predicted, the potential is constant when the modes are outside horizon. Two modes enter the horizon during radiation era and the amplitudes decrease as 𝑎-2. The resulting amplitudes in the matter era are strongly suppressed. During the matter era the potential is a constant on all scales. The long wavelength mode is only suppressed by a factor of 9/10 coming from the radiation-to-matter transition.
In Problem 6.1 we will be asked to derive an analytic solution for 𝛷 superhorizon evolution:
(6.167) 𝛷(𝑎, 𝐤) = 2𝓡𝑖/30𝑦3 [16√(1 + 𝑦) + 9𝑦3 + 2𝑦2 - 8𝑦 - 16] (superhorizon),
where 𝑦 ≡ 𝑎/𝑎eq. It gives the same result: this solution reduces to a constant at both early times (𝑦 ≪ 1) and late times (𝑦 ≫ 1) and accounts for the 9/10 factor in the transition described above.
Exercise 6.14 Consider the evolution equation (6.124) for the gravitational potential. Show that during the dark energy-dominated era, this equation can be written as
(6.168) 𝑑2𝛷/𝑑𝑎2 + 5/𝑎 𝑑𝛷/𝑑𝑎 + 3/𝑎2𝛷 = 0,
where 𝑎(𝜂) = [1 + 𝐻𝛬(𝜂0 - 𝜂)]-1, with 𝐻𝛬 =const. Note that this equation is valid on all scales. Show that the growing mode solution decays as 𝛷 ∝ 𝑎-1.
[Solution] From (6.124)
(a) 𝛷ʺ + 3𝓗𝛷ʹ + (2𝓗ʹ + 𝓗2)𝛷 = 4π𝐺𝑎2𝛿𝑃.
In the dark energy-dominated era we have 𝛿𝑃 = 0 and 𝐻𝛬 = const. From the corollary above (2.164)
(b) 𝓗 ≡ 𝑎ʹ/𝑎 = 𝐻𝑎 = 𝑎̇/𝑎2 = 𝑎𝐻𝛬, 𝑑𝜂 = 𝑑𝑡/𝑎(𝑡),
(c) ∫ 𝑡0𝑡 (𝑑𝑎/𝑑𝑡)/𝑎2 𝑑𝑡 = ∫ 1𝑎 𝑑𝑎/𝑎2 = ∫ 𝜂0𝜂 𝐻𝛬 𝑑𝜂 ⇒ [- 1/𝑎]1𝑎 = 𝐻𝛬(𝜂0 - 𝜂), ⇒ 𝑎(𝜂) = 1/[1 + 𝐻𝛬(𝜂0 - 𝜂)].
(d) 𝛷ʹ = 𝑑𝛷/𝑑𝜂 = 𝑑𝑎/𝑑𝜂 𝑑𝛷/𝑑𝑎 = 𝑎𝓗 𝑑𝛷/𝑑𝑎 = 𝑎2𝐻𝛬 𝑑𝛷/𝑑𝑎
(e) 𝛷ʺ = 𝑎2𝐻𝛬 𝑑/𝑑𝑎 (𝑎2𝐻𝛬 𝑑𝛷/𝑑𝑎) = 𝑎4𝐻𝛬2 𝑑2𝛷/𝑑𝑎2 + 2𝑎3𝐻𝛬2 𝑑𝛷/𝑑𝑎.
(f) 2𝓗ʹ + 𝓗2 = 2(𝑎𝐻𝛬)ʹ + (𝑎𝐻𝛬)2 = 2𝑎ʹ𝐻𝛬 + 𝑎2𝐻𝛬2 = 2𝑎2𝐻𝛬2 + 𝑎2𝐻𝛬2 = 3𝑎2𝐻𝛬2. So we have,
(g) (𝑎4𝐻𝛬2 𝑑2𝛷/𝑑𝑎2 + 2𝑎3𝐻𝛬2 𝑑𝛷/𝑑𝑎) + 3𝑎𝐻𝛬 𝑎2𝐻𝛬 𝑑𝛷/𝑑𝑎 + 3𝑎2𝐻𝛬2 = 0. ⇒ 𝑑2𝛷/𝑑𝑎2 + 5/𝑎 𝑑𝛷/𝑑𝑎 + 3/𝑎2𝛷 = 0.
Considering the ansaz 𝛷 = 𝑎𝑥, we get
(h) 𝑥(𝑥 - 1)𝑎𝑥 - 2 - 5/𝑎 𝑥𝑎𝑥 - 1 + 3/𝑎2 𝑎𝑥 = 0, ⇒ 𝑥2 + 4𝑥 + 3 = (𝑥 + 1)(𝑥 + 3) = 0. ⇒ 𝑥 = {-1, -3}
Hence the growing mode solution decays as 𝛷 ∝ 𝑎-1. ▮
6.3.2 Clustering of Dark Matter
Next, the growth of dark matter perturbation will be described. In the relativistic framework we will reproduce and extend the evolution of subhorizon perturbations of a pressureless fluid treated before.
Matter era
In matter era since matter is the dominant component, the Poisson equation reads
(6.169) ∇2𝛷 ≈ 4π𝐺𝑎2𝜌̄𝑚∆𝑚.
The solution for the comoving density contrast ∆𝑚 can be obtained directly from our previous result for 𝛷. Using (6.160) and 2𝜌̄𝑚 ∝𝑎-1,
(6.170) ∆𝑚(𝑎, 𝐤) = 𝑘2𝛷/4π𝐺𝑎2𝜌̄𝑚 = 𝐶˜1(𝐤) + 𝐶˜2(𝐤)𝑎-3/2. (matter era), [RE (5.14) ∇2 = -𝑘2 in Fourier mode]
just as in the Newtonian treatment, bu now valid on all scales. The growing mode of ∆𝑚 evolves as 𝑎 outside the horizon, while density contrast 𝛿𝑚 stays constant. Inside the horizon, 𝛿𝑚 ≈ ∆𝑚 and 𝛿𝑚 in both gauges evolve as the scale factor 𝑎.
Dark energy era
Since dark energy has no density fluctuations, the Poisson equation is still of form (6.169). since 𝑎2𝜌̄𝑚 ∝ 𝑎-1, we have 𝛷 ∝ ∆𝑚/𝑎. The Einstein equation (6.124) then implies
(6.171) ∂𝜂2(∆𝑚/𝑎) + 3𝓗∂𝜂(∆𝑚/𝑎) + (2𝓗ʹ + 𝓗2(∆𝑚/𝑎) = 0, ⇒
(6.172) ∆𝑚ʺ + 𝓗∆𝑚ʹ + (𝓗ʹ - 𝓗2)∆𝑚 = 0
Combing the Friedmann equations (2.156) and (2.157) for a universe with matter and dark energy gives
(6.173) 2(𝓗ʹ - 𝓗2) = (𝓗ʹ + 𝓗2) - 3𝓗2 = -8π𝐺𝑎2𝑃̄ - 8π𝐺𝑎2𝜌̄ = +8π𝐺𝑎2𝜌̄𝛬 - 8π𝐺𝑎2(𝜌̄𝑚 + 𝜌̄𝛬) = -8π𝐺𝑎2𝜌̄𝑚, [verification needed]
(6.172) becomes
(6.174) ∆𝑚ʺ + 𝓗∆𝑚ʹ - 4π𝐺𝑎2𝜌̄𝑚∆𝑚 = 0.
This is similar to the Newtonian equation (5.62), but is now valid on all scales. In the dark energy-dominated regime, we 𝓗2 ≫ 4π𝐺𝑎2𝜌̄𝑚 and we can drop the last term in (6.174) to get
(6.175) ∆𝑚ʺ - 1/𝜂 ∆𝑚ʹ ≈ 0,
which has the final equation
(6.176) ∆𝑚(𝑎, 𝐤) = 𝑘2𝛷/4π𝐺𝑎2𝜌̄𝑚 = 𝐶˜1(𝐤) + 𝐶˜2(𝐤)𝑎-2. (dark energy era),
[Derivation (2.149) 𝑎 ∝ -1/𝜂. ⇒ 𝓗 = 𝑎ʹ/𝑎 = (- 1/𝜂)ʹ/(- 1/𝜂) = - 1/𝜂. ⇒ ∆𝑚ʺ - 1/𝜂 ∆𝑚ʹ = 0. ⇒ ∆𝑚 = 𝐶1 + 𝐶2𝜂2 = 𝐶1 + 𝐶2𝑎-2. ▮]
where we used -𝜂 ∝𝑎-1. [correction: 𝜂 → -𝜂]. This recovers the suppression od the growth of structure that we found in the previous chapter, but it now hold on all scales.
Exercise 6.15 Show that (6.176) also follows directly from the solution to (6.168).
[Solution] In Exercise 6.14, we showed that 𝛷 ∝ 𝑎-1, 𝑎-3. Since 𝛷 ∝ ∆𝑚/𝑎, (u)∆𝑚 ∝ 𝑎0 = Const, 𝑎-2(/u). ▮
Radiation era
During the radiation era matter is a subdominant and we must work with continuity and Euler equations. In Section 6.1.3 we showed that this implies [RE (6.87)]
(6.177) 𝛿ʺ𝑚 + 𝓗𝛿ʹ𝑚 = ∇2𝛷 + 3(𝛷ʺ + 𝓗𝛷ʹ),
where 𝛷 = 𝛷𝑟 + 𝛷m is sourced by both radiation and matter. The contribution from 𝛷𝑟 is rapidly oscillating on subhorizon scales, while 𝛷m is a constant. The solution 𝛿𝑚 inherits a "fast mode" by 𝛷𝑟 and "slow mode" by 𝛷m. It turns out that the fast mode is suppressed by a factor of (𝓗/𝑘)2 relative to the slow mode [Weinberg]. This reflects the fact that the matter can't react to the fast change in the gravitational potential and effectively only evolves in response to the time-averaged potential. As a result 𝛿𝑚 is sourced by even deep in the radiation era. Using ∇2𝛷 ≈ ∇2𝛷𝑚 = 4π𝐺𝑎2𝜌̄𝑚𝛿𝑚 and 𝛷ʺ = 𝛷ʹ ≈ 0, we get
(6.178) 𝛿ʺ𝑚 + 𝓗𝛿ʹ𝑚 - 4π𝐺𝑎2𝜌̄𝑚𝛿𝑚 ≈ 0,
where 4π𝐺𝑎2𝜌̄𝑚 = 3/2 𝛺m𝓗2.[verification needed] The conformal Hubble parameter for a universe with matter and radiation is
(6.179) 𝓗/𝓗0 = 𝛺m/√𝛺𝑟 √(1 + 𝑦)/𝑦, 𝑦 ≡ 𝑎/𝑎eq,
where 𝑎eq = 𝛺𝑟/𝛺m is the scale factor at matter-radiation equality. Using 𝑦 as the time variable, (6.178) becomes so-called Mészáros equation
(6.180) 𝑑2𝛿𝑚/𝑑𝑦2 + (2 + 3𝑦)/2𝑦(1 + 𝑦) 𝑑𝛿𝑚/𝑑𝑦 - 3/2𝑦(1 + 𝑦) 𝛿𝑚 = 0, whose solutions are
(6.181) 𝛿𝑚 ∝ { 1 + 3/2 𝑦; (1 + 3/2 𝑦) ln[{√(1 + 𝑦) + 1}/{√(1 + 𝑦) - 1}] - 3√(1 + 𝑦).
In the limit 𝑦 ≪ 1 (RD) the growing mode solution is 𝛿𝑚 ∝ ln 𝑦 ∝ ln 𝑎 i.e. grow logarithmically. In the limit 𝑦 ≫ 1 (MD) the solution is 𝛿𝑚 ∝ 𝑦 ∝ 𝑎 significantly.
Fig. 6.6 shows numerical solutions for the dark matter density contrast evolution for 3 Fourier modes. Notice that the 𝑘 > 𝑘eq receives a small boost at horizon crossing before setting into the slow logarithmic growth.
6.3.3 Matter Power Spectrum
We explain the shape of power spectrum for clustering of matter fluctuation. At a time 𝜂𝑖 when all modes were still outside the Hubble radius, we take the initial power spectrum to be scale invariant, so that 𝑘3𝒫𝑚(𝜂𝑖, 𝑘) = const. We would like to see how the scale dependence of the spectrum evolves with time. (See also Section 5.2.3)
Consider the time 𝜂eq. Modes with 𝑘 < 𝑘eq are outside the horizon and the spectrum must have the same initial spectrum (see Fig. 6.7). Modes with 𝑘 > 𝑘eq evolved as ln 𝑎 inside the horizon in the radiation era. Their amplitude is enhanced by a factor of ln(𝑎eq/𝑎𝑘), where 𝑎𝑘 is the moment of horizon crossing of mode 𝑘. Since 𝑘 = (𝑎𝐻)𝑘 ∝ 𝑎𝑘-1 during the radiation era, this gives the (ln 𝑘)2 scaling of the spectrum for 𝑘 > 𝑘eq.
Next, we take a time 𝜂0 of today. All subhorizon modes grows as 𝑎. For 𝑘 < 𝑘eq we have 𝑘3𝒫𝑚 ∝ (𝑎eq/𝑎𝑘)2 ∝ 𝑘4, where we used 𝑘 = (𝑎𝐻)𝑘 ∝ 𝑎𝑘-1/2 in matter era. For 𝑘 < 𝑘eq we instead get 𝑘3𝒫𝑚 ∝ (𝑎0/𝑎eq)2ln(𝑎eq/𝑎𝑘)2 ∝(ln 𝑘)2 as before. Combining these results, we have
(6.182) 𝒫𝑚(𝜂0, 𝑘) = { 𝑘-3 𝑘 < 𝑘0; 𝑘 𝑘0 < 𝑘 < 𝑘eq; 𝑘-3(ln 𝑘)2 𝑘 > 𝑘eq.
By definition the regime 𝑘 < 𝑘0, with 𝑘0 = 𝑎0𝐻0 ≈ 3 × 10-4 𝘩 Mpc-1, corresponds to superhorizon modes today. The scaling of the spectrum 𝑘 > 𝑘0 on subhorizon mode is the same as that in Section 5.2.3.
6.4 Evolution of Photons and Baryons
Fig. 6.8 shows the evolution of perturbations in dark matter, baryons and photons for a representative Fourier mode. Initially, the fluctuations in all components are of equal size (up to a factor of 4/3). Before decoupling , the baryons are tightly coupled to a photons and oscillate after horizon crossing. The dark matter experiences a slow logarithmic growth during the radiation era a more rapid power law growth during the matter era. This explain why 𝛿𝑐 ≫ 𝛿𝑏 at decoupling. After decoupling, the baryons lose the pressure support of photons and fall into the gravitational potential wells created by the dark matter. The density contrasts of dark matter and baryons eventually become equal again (see Exercise 5.2). It is crucial that the clustering of dark matter had a head start and then aided the growth of the baryon perturbations. Without the dark matter-assisted growth, the baryon wouldn't be able to cluster fast enough to explain the formation of galaxies.
We will study the evolution of photons and baryons prior to decoupling. During that time, the photons and baryons acted as a single fluid with pressure provided by photons and extra mass density by the baryons. To build up intuition we will start by ignoring the baryons and study the photon perturbations alone.9 After that, we will how this dynamics is modified by the presence of baryons.
6.4.1 Radiation Fluctuations
Consider the evolution of perturbation in the relativistic perfect fluid during the radiation era. Because the radiation component dominates we use the same trick and consider the Poisson equation, which now reads
(6.183) ∇2𝛷 = 3/2 𝓗2∆𝑟,
In Fourier space, we have
(6.184) ∆𝑟(𝜂, 𝐤) = -2/3 (𝑘𝜂)2𝛷(𝜂, 𝐤),
and using (6.165) we find
(6.185) ∆𝑟(𝜂, 𝐤) = -4𝓡𝑖 [sin(𝜑) - 𝜑 cos(𝜑)]/𝜑 (radiation era),
where 𝜑 ≡ 𝑘𝜂/√3. This solution is again valid on all scales. Taking the limits 𝜑 ≪ 1 and 𝜑 ≫ 1 gives the solutions as follows
(6.186) ∆𝑟(𝜂, 𝐤) ≈ { -4/9 𝓡𝑖(𝑘𝜂)2 (superhorizon); 4𝓡𝑖 cos(1/√3 𝑘𝜂) (subhorizon).
We see that the comoving density contrast grows as ∆𝑟 ∝ 𝜂2 ∝ 𝑎2 on superhorizon scales, while it oscillates with a constant amplitude on subhorizon scales.
Exercise 6.16 Using
(6.187) 𝛿𝑟 = -2/3 (𝑘𝜂)2𝛷 - 2𝜂𝛷ʹ - 2𝛷,
determine the solution for 𝛿𝑟 from (6.165). What are the superhorizon and subhorizon limits of the solution?
[Solution] Defining 𝜑 ≡ 𝑘𝜂/√3
(a) 𝛿𝑟 = -2𝜑2𝛷 - 2𝜑 𝑑𝛷/𝑑𝜑 - 2𝛷,
we get
(b) 𝛿𝑟 = -4𝓡𝑖 [(𝜑2 - 2)𝜑 cos(𝜑) + 2(𝜑2 -1) sin(𝜑) ]/𝜑3
(c) 𝛿𝑟 → { 4𝓡𝑖 cos(𝜑) 𝜑 ≫ 1 (subhorizon); 4/3 𝓡𝑖 𝜑 ≪ 1 (superhorizon). ▮
Next, we consider the evolution in the matter era. Since the radiation fluctuations are subdominant, we must use the continuity and Euler equations. In Section 6.1.3 we showed that the radiation density contrast satisfies
(6.188) 𝛿𝑟ʺ - 1/3 ∇2𝛿𝑟 = 4/3 ∇2𝛷 + 4𝛷ʺ ⇐ 𝛿𝑟ʹ = -4/3 𝛁 ⋅ 𝐯𝑟 + 4𝛷ʹ, 𝐯𝑟ʹ = -1/4 𝛁𝛿𝑟 - 𝛁𝛷,
Recall that during matter domination, the gravitational potential is a constant on all scales, so that
(6.189) 𝛿𝑟ʺ - 1/3 ∇2𝛿𝑟 = 4/3 ∇2𝛷 = const.
This is the equation of a harmonic oscillator with a constant driving force. The subhorizon fluctuations in the radiation density oscillate with a constant amplitude around a shifted equilibrium point, -4𝛷0(𝐤), where 𝛷0(𝐤) is the 𝑘-dependent amplitude of the gravitational potential in the matter era. This 𝑘-dependence arises from the initial conditions and nontrivial transfer function of the dark matter fluctuations. The solution for the density contrast is
(6.190) 𝛿𝑟(𝜂, 𝐤) = 𝐶(𝐤) cos(𝜑) + 𝐷(𝐤) sin(𝜑) - 4𝛷0(𝐤),
where 𝜑 ≡ 𝑘𝜂/√3.
6.4.2 Photon-Baryon Fluid
So far we have ignored the effects of baryons on the radiation fluid (except for their role in suppressing the photon aniso tropic stress). Let us fix this. We will work in the so-called tight-coupling approximation, where the coupling between photons and baryons is so strong that they can be treated as a single photon-baryon fluid with velocity 𝐯𝑏 = 𝐯𝛾. Only the combined momentum density of the photons baryons is now conserved:
(6.191) 𝐪 = (𝜌̄𝛾 + 𝑃̄𝛾)𝐯𝛾 + (𝜌̄𝑏 + 𝑃̄𝑏)𝐯𝑏 = 4/3 (1 + 𝑅)𝜌̄𝛾𝐯𝛾, 𝑅 ≡ 3/4 𝜌̄𝑏/𝜌̄𝛾 = 0.6 (𝛺𝑏𝘩2/0.02)(𝑎/10-3).
The fractional contribution from the baryons is characterized by the dimensionless parameter 𝑅. This parameter is small at early times, but grows linearly with 𝑎(𝑡) and becomes of order one around the time of recombination.
Recall the Euler equation for the evolution of the momentum density
(6.192) 𝐪ʹ + 4𝓗𝐪 = -(𝜌̄ + 𝑃̄)𝛁𝛹 - 𝛁𝛿𝑃,
where 𝛹 ≈ 𝛷 in the absence of anisotropic stress. Substituting (6.191) the left-hand side can be written as
(6.193) 𝐪ʹ + 4𝓗𝐪 = ∂𝜂(𝑎4𝐪)/𝑎4 = 4/3 𝜌̄𝛾[(1 + 𝑅)𝐯𝛾]ʹ,
where we have used that 𝑎4𝜌̄𝛾 is a constant. Inserting 𝜌̄ + 𝑃̄ = 4/3 (1 + 𝑅)𝜌̄𝛾 and 𝛿𝑃 = 1/3 𝜌̄𝛾𝛿𝛾 on the right-hand side, we get
(6.194) -(𝜌̄ + 𝑃̄)𝛁𝛹 - 𝛁𝛿𝑃 = -4/3 𝜌̄𝛾[(1 + 𝑅)𝛁𝛹 + 1/4 𝛁𝛿𝛾].
Combining the two equations then gives
(6.195) [(1 + 𝑅)𝐯𝛾]ʹ ← inertial mass = -1/4 𝛁𝛿𝛾 - (1 + 𝑅)𝛁𝛹 ← gravitational mass.
For 𝑅 = 0 this reduces to the Euler equation for the radiation fluid in (6.188). The correction ti this equation are: The coupling to the baryons adds extra "weight" to the photon-baryon fluid. This increases both the momentum density and the gravitational force term by a factor of (1 + 𝑅). The baryons, on the other hand, don't contribute to the pressure, so the pressure force does not receive this factor.
Since the scattering of photons and baryons doesn't exchange energy, the continuity equation in (6.188) does not get modified and still reads
(6.196) 𝛿𝑟ʹ = -4/3 𝛁 ⋅ 𝐯𝛾 + 4𝛷ʹ.
Combining the continuity and Euler equations we find
(6.197) 𝛿𝑟ʺ + 𝑅ʹ/(1 + 𝑅) 𝛿𝑟ʹ - 1/3(1 + 𝑅) ∇2𝛿𝑟 ← pressure = 4/3 ∇2𝛹 ← gravity + 4𝛷ʺ + 4𝑅ʹ/(1 + 𝑅) 𝛷ʹ.
which is the fundamental equation for the evolution of density perturbation in the photon-baryon fluid.
From the pressure term in (6.197) we can read off the sound speed of the photon-baryon fluid
(6.197) 𝑐𝑠2 ≡ 1/3(1 + 𝑅).
This is consistent with the definition of the definition of the adiabatic sound speed 𝑐𝑠2 = 𝛿𝑃/𝛿𝜌. To see this, we use 𝛿𝑃 = 𝛿𝑃𝛾 = 1/3 𝛿𝜌𝛾 and 𝛿𝜌 = 𝛿𝜌𝛾 + 𝛿𝜌𝑏, together with 𝛿𝜌𝑏 = 3/4 (𝜌̄𝑏/𝜌̄𝛾)𝛿𝜌𝛾 (for adiabatic perturbations).
6.4.3 Cosmic Sound Waves
The dynamics associated with (6.197) is rather complex and will be discussed in detail in Chapter 7.
Acoustic oscillations
For simplicity let us ignore the effects of gravity and consider solutions to the homogeneous equation:
(6.199) 𝛿𝑟ʺ + 𝑅ʹ/(1 + 𝑅) 𝛿𝑟ʹ - 1/3(1 + 𝑅) ∇2𝛿𝑟 = 0.
There re two timescale: the expansion time and the oscillation time. On small scale, 𝑘 ≫ 𝓗/𝑐𝑠, the latter is much shorter than the former. A WKB approximation can be used to the damped harmonic oscillator equation: [Wikipedia WKB approximation]
(6.200) 𝛿𝑟(𝜂, 𝐤) = 𝐶(𝐤) cos(𝑘𝑟𝑠)/(1 + 𝑅)1/4 + 𝐷(𝐤) sin(𝑘𝑟𝑠)/(1 + 𝑅)1/4,
where 𝑟𝑠(𝜂) ≡ ∫𝜂0 𝑐𝑠(𝜂ʹ) 𝑑𝜂ʹ is the sound horizon at the time 𝜂. At the photon decoupling, 𝜂*, the sound horizon 𝑟𝑠(𝜂*) ≈ 145 Mpc (or 500 million light-years). The functions 𝐶(𝐤) and 𝐷(𝐤) are fixed by superhorizon initial conditions. For the adiabatic initial conditions, the superhorizon modes are time independent, so the sine solution is not excited, 𝐷(𝐤) = 0. The amplitude of cosine solution 𝐶(𝐤) is determined by the value of the perturbation at horizon crossing. An important feature of solution is that all Fourier modes of a given wavelength reach the extrema at the same time in any direction. This phase coherence allows for the constructive interference of many waves, which leaves an imprint in cosmological observables.
A numerical solution for the acoustic oscillations in the photon-baryon fluid is shown in Fig. 6.9. An important feature that is not captured by our simplified analysis is the damping of the fluctuations, which arises because the photons diffuse out of the regions high density into those of low density, washing out the density contrast. The so-called diffusion damping is especially relevant for small-scale fluctuations (high-𝑘 modes) and to describe it requires going beyond the tight-coupling approximation. A more accurate treatment must also include the time-dependent gravitational driving force that we ignored. In Chapter 7 we will treat the more subtle physics of the sound waves in the primordial plasma.
CMB anisotropies
Looking at the CMB, we are seeing a snapshot of the primordial sound waves at the moment of sound decoupling. From (6.200) that the oscillation frequency depends on wavenumber 𝑘, meaning that different modes decouple at different phase and therefore different amplitudes at last-scattering (see Fig. 6.10). Evaluating the solution at decoupling, 𝜂 = 𝜂*, gives the 𝑘-dependent amplitude of the fluctuations at last scattering. The amplitude has extreme at
(6.201) 𝑘𝑛 = 𝑛π/𝑟𝑠(𝜂*), with 𝑛 = 1, 2, ∙ ∙ ∙ .
After projecting the Fourier modes onto the spherical surface of last-scattering, these becomes the peaks in the angular power spectrum of the CMB anisotropies. Note that the Power spectrum measures ∣𝛿𝑟∣2 so the maxima and minima in 𝛿𝑟 both become peaks in the power spectrum, The positions of the peaks are determined by a combination of the sound horizon at decoupling and the angular diameter distance to the surface of last-scattering. The heights of the peaks carry information about the amount of dark matter and baryons in the universe. The size of the damping on small scales depends on the density of neutrinos. This is how the measurements of the CMB anisotropies by the WMAP, Planck satellites and other ground-based experiments allowed precise measurements of the cosmological parameters and revolutionized the field of cosmology. It will be described in much more detail in Chapter 7.
Baryon acoustic oscillations*
The same oscillations in the CMB anisotropies also leave an imprint in the clustering of galaxies. This arises because photons and baryons oscillates together before decoupling. The different Fourier mode of the baryons decouple at different phases in the evolution. Te initial conditions for gravitational growth of the barons include th oscillation of the photon-baryon fluid. This oscillatory feature gets transferred to the gravitational potential and the matter fluctuations, but because baryons are only about 15% of the total matter density, the effect is smaller than in the CMB. Since correlations in the galaxy distributions are inherited from the correlations in the matter density, these baryon acoustic oscillations (BAO) are imprinted in the galaxy power spectrum (see Fig. 6.11). In the following, a simple analytic derivation of the BAO signal will be given [12].
The time when the baryons are released from the drag of the photons is known as the drag epoch. In fact the baryons decouple slightly later than the photons at 𝑧𝑏 ≈ 1060 (compared to 𝑧* ≈ 1090). After the drag epoch, the baryons behave as pressureless matter and we can write the total matter density contrast as
(6.202) 𝛿𝑚 = 𝑓𝑏𝛿𝑏 + (1 - 𝑓𝑏)𝛿𝑐,
where 𝑓𝑏 ≡ 𝜌𝑏/𝜌𝑚 is the fractional baryon density. Near decopupling the solution for the totalmatter density is given by (6.181):
(6.203) 𝛿𝑚(𝜂, 𝐤) = 𝐶1(𝐤) 𝐷1(𝑦) + 𝐶2(𝐤) 𝐷2(𝑦), 𝑦(𝜂) ≡ 𝑎(𝜂)/𝑎eq.
(6.204) 𝐷1(𝑦) = 2/3 + 𝑦 ≈ 𝑦,
𝐷2(𝑦) = 𝐷1(𝑦) n[{√(1 + 𝑦) + 1}/{√(1 + 𝑦) - 1}] - 2√(1 + 𝑦) ≈ 8/45 𝑦-3/2.
The growing mode solution at late time is 𝛿𝑚 ≈ 𝐶1(𝐤) 𝑦. We would like to write this solution in terms of its initial conditions at baryon decoupling. To do this we match 𝛿𝑚 and 𝛿𝑚ʹ at the end of the drag epoch. The matching conditions are, using (6.203) and (6.202)
(6.205) 𝐶1(𝐤) 𝐷1(𝜂𝑑) + 𝐶2(𝐤) 𝐷2(𝜂𝑑) = 𝑓𝑏𝛿𝑏(𝜂𝑑) + (1 - 𝑓𝑏)𝛿𝑐(𝜂𝑑),
𝐶1(𝐤) 𝐷1ʹ(𝜂𝑑) + 𝐶2(𝐤) 𝐷2ʹ(𝜂𝑑) = 𝑓𝑏𝛿𝑏ʹ(𝜂𝑑) + (1 - 𝑓𝑏)𝛿𝑐ʹ(𝜂𝑑).
Solving this for 𝐶1(𝐤) and only only keeping baryonic contribution which carries the oscillatory feature, we find
(6.206) 𝐶1(𝐤) = 𝑓𝑏 𝐶2ʹ/(𝐷1𝐷2ʹ - 𝐷1ʹ𝐷2) [𝛿𝑏(𝜂𝑑, 𝐤) - 𝐷2/𝐷2ʹ𝛿𝑏ʹ(𝜂𝑑, 𝐤)], [verification needed]
where all functions of time are evaluated at 𝜂𝑑. Note that ∂𝜂𝑓 = 𝓗𝑦 ∂𝑦𝑓. Using 𝑦𝑑 ≫ 1, replacing all growth functions 𝐷𝑖 by their asymptotic expressions, we get
(6.207) 𝛿𝑚(𝜂, 𝐤) = 𝐶1(𝐤) ≈ 3𝑓𝑏/5 [𝛿𝑏(𝜂𝑑, 𝐤) + 2/3 (𝑘𝜂𝑑) 𝑣𝑏(𝜂𝑑, 𝐤)] 𝑎/𝑎𝑑,
where we used 𝛿𝑏ʹ = 𝑘𝑣𝑏. On smaller scales than the horizon at the drag epoch, we have 𝑘𝜂𝑑 ≫ 1 and the second term, proportional to the velocity 𝑣𝑏 dominates. This is called the velocity overshoot. When the baryons are released at the drag epoch, they move according to their velocity and generate a new density perturbation. This is dominant effect on small scales.
As long as the tight-coupling approximation holds, we have 𝑣𝑏 = 𝑣𝛾 = 3/4 𝛿𝛾ʹ/𝑘. The cosine contribution in the solution (6.200) for 𝛿𝛾 then leads to a dominant sine contribution in the solution (6.207) for 𝛿𝑚. A recent measurement of the BAO signal is shown in 6.11. It is rather amazing how this signal arising from primordial sound waves in the early universe is so clearly visible to the clustering of the galaxies billions of years later. In position space space, the BAO feature maps to a peak around 110𝘩-1Mpc. The position of this peak is an important "standard ruler." It depends on the sound horizon at the drag epoch and the angular diameter distance to the the observed objects. Measurements of the BAO help to break degeneracies in the CMB data and played an important role in the measurements of the cosmological parameters (see Chapter 7).
6.5 Gravitational Waves
On September 14, 2015, when the LIGO(Laser Interferometer Gravitational-Wave Oberservatory) detected the first gravitational waves (GWs) from the merger of two black holes, a new era of science was initiated! This detection marked the beginning of multi-messenger astronomy and in the future GWs may provide a new window into the early universe. Some mathematical background on cosmological GWs useful in Chapter 7 and 8 will be collected here. Further details can be found in [15].
GWs are tensor perturbations to the spatial metric,
(6.208) 𝑑𝑠2 = 𝑎2(𝜂) [-𝑑𝜂2 + (𝛿𝑖𝑗 + 𝘩𝑖𝑗)𝑑𝑥𝑖𝑑𝑥𝑗].
Since the perturbation 𝘩𝑖𝑗 is symmetric (𝘩𝑖𝑗 = 𝘩𝑗𝑖), transvers (∂𝑖𝘩𝑗𝑖 = 0), and traceless (𝘩𝑗𝑖 = 0), it contains 6 - 3 -1 = 2 independent modes (corresponding to the 2 polarizations of GW).[verification needed] We write the Fourier modes of 𝘩𝑖𝑗 as
(6.209) 𝘩𝑖𝑗(𝜂, 𝐤) = ∑𝜆=+,× 𝘩𝜆(𝜂, 𝐤) 𝜖𝜆𝑖𝑗(𝐤̂),
where 𝜖𝜆𝑖𝑗(𝐤̂) are two independent polarization tensors and 𝘩𝜆(𝜂, 𝐤) are the corresponding mode functions. The polarization tensors can be taken to be real and satisfy 𝜖𝜆𝑖𝑗(𝐤̂) = 𝜖𝜆𝑖𝑗(-𝐤̂), so that 𝘩𝜆(𝜂, 𝐱) is real if 𝘩*𝜆(𝜂, 𝐤) = 𝘩𝜆(𝜂, -𝐤). The polarization tensors are symmetric (𝜖𝜆𝑖𝑗 = 𝜖𝜆𝑗𝑖), transverse (𝑘̂𝑖𝜖𝜆𝑖𝑗 = 0) and traceless (𝜖𝜆𝑖𝑖 = 0). Our normalization for polarization basis can be
(6.210) ∑𝑖,𝑗 𝜖𝜆𝑖𝑗𝜖𝜆ʹ𝑖𝑗 = 2𝛿𝜆𝜆ʹ. [verification needed]
Explicitly, the polarization tensors can be written as
(6.211) 𝜖+𝑖𝑗(𝐤̂) = 𝑚̂𝑖𝑚̂𝑗 - 𝑛̂𝑖𝑛̂𝑗, 𝜖×𝑖𝑗(𝐤̂) = 𝑚̂𝑖𝑚̂𝑗 + 𝑛̂𝑖𝑛̂𝑗
where 𝐦̂ and 𝐧̂ are two unit vectors orthogonal to 𝐤̂ and to each other. For a GW with a wavevector pointing in the 𝑧-direction direction, 𝐤̂ = (0, 0, 1), we can choose 𝐦̂ = 𝐱̂ and 𝐧̂ = 𝐲̂, so that
⌈ 1 0 0 ⌉ ⌈ 0 1 0 ⌉ ⌈ 𝘩+ 𝘩× 0 ⌉
(6.212) 𝘩𝑖𝑗 = 𝘩+┃0 -1 0┃ + 𝘩×┃1 0 0┃ = ┃𝘩× -𝘩+ 0┃ * ipad view
⌊ 0 0 0 ⌋ ⌊ 0 0 0 ⌋ ⌊ 0 0 0 ⌋
⌈ 1 0 0 ⌉ ⌈ 0 1 0 ⌉ ⌈ 𝘩+ 𝘩× 0 ⌉
(6.212) 𝘩𝑖𝑗 = 𝘩+┃0 -1 0┃ + 𝘩×┃1 0 0┃ = ┃𝘩× -𝘩+ 0┃ * pc view
⌊ 0 0 0 ⌋ ⌊ 0 0 0 ⌋ ⌊ 0 0 0 ⌋
Sometimes, it's useful to work in the so-called helicity basis, where
(6.213) 𝜖±2𝑖𝑗 ≡ (𝜖+𝑖𝑗 ± 𝑖𝜖×𝑖𝑗)/2, 𝘩±2 ≡ 𝘩+ ∓ 𝑖𝘩×.
Under a rotation by an angle 𝜓 around the wavenumber 𝐤, we have 𝘩±2 ↦ 𝑒±2𝑖𝜓𝘩±2, which shows that the mode 𝘩±2 describe states of helicity +2 and -2 (also called "right-handed" and "left-handed" polarization respectively).
Problem 6.4 shows that the linearlized Einstein equation implies following evolution equation for tensor
(6.214) 𝘩𝑖𝑗ʺ + 2𝓗𝘩𝑖𝑗ʹ - ∇2𝘩𝑖𝑗 = 16π𝐺𝑎2𝛱̂𝑖𝑗,
where 𝛱̂𝑖𝑗 is the transvers, traceless part of the anisotropic stress. In 𝛱̂𝑖𝑗 = 0, this equation describes the free propagation of GWs in an expanding universe. By defining 𝑓𝑖𝑗 ≡ 𝑎(𝜂)𝘩𝑖𝑗, we can remove the Hubble friction term. Then each polarization mode satisfies
(6.215) 𝑓𝜆ʺ + (𝑘2 - 𝑎ʺ/𝑎)𝑓𝜆 = 0. [verification needed]
Let us solve this for a generic scale factor 𝑎(𝜂) ∝ 𝜂𝛽, which includes radiation domination (𝛽 = 1), matter domination (𝛽 = 2) and inflation (𝛽 ≈ -1) as special cases. The solution is
(6.216) 𝘩𝜆(𝜂, 𝐤) = 𝐶𝜆(𝐤)/𝑎(𝜂) 𝜂𝑗𝛽-1(𝑘𝑛) + 𝐷𝜆(𝐤)/𝑎(𝜂) 𝜂𝑦𝛽-1(𝑘𝑛),
where 𝑗𝛽 and 𝑦𝛽 are spherical Bessel functions (see Appendix D) and the constants 𝐶𝜆(𝐤) and 𝐷𝜆(𝐤) must be fixed by the initial conditions.
Note that for a power-law scale factor, we have 𝑎ʺ/𝑎 ∝ 𝓗2. On sub-Hubble scales, 𝑘 ≫ 𝓗, we can drop the 𝑎ʺ/𝑎 term in (6.215) and the solution is
(6.217) 𝘩𝜆(𝜂, 𝐤) = 𝐶𝜆(𝐤)/𝑎(𝜂) 𝑒𝑖𝑘𝑛 + 𝐷𝜆(𝐤)/𝑎(𝜂) 𝑒𝑖𝑘𝑛 𝑒-𝑖𝑘𝑛 (for 𝑘 ≫ 𝓗),
which we can check also follows from the 𝑘𝑛 ≫ 1 limit of (6.216). On sub-Hubble scales, we get the expected plane wave solutions with an amplitude that decays as 𝑎-1. On super-Hubble scales, 𝑘 ≪ 𝓗, we instead drop 𝑘2 term and the solution becomes
(6.218) 𝘩𝜆(𝜂, 𝐤) = 𝐶𝜆(𝐤)/𝑎(𝜂) + 𝐷𝜆(𝐤) ∫ 𝑑𝜂/𝑎2(𝜂) (for 𝑘 ≪ 𝓗).
The second term decays with the expansion of the universe, so that the growing mode of the GW is a constant on super-Hubble scales.10
In cosmology we are interested in power spectrum of a stochastic background of GWs, 𝒫𝘩(𝑘) ≡ (2π2/𝑘3)∆2𝘩(𝑘). We define this power spectrum, so that the variance is
(6.219) ∑𝑖,𝑗⟨𝘩2𝑖𝑗(𝐱)⟩ = ∫ 𝑑 ln ∆2𝘩(𝑘),
where we suppressed the time dependence. The power spectrum for the individual polarization modes then is
(6.220) ⟨𝘩𝜆(𝐤) 𝘩𝜆ʹ(𝐤ʹ)⟩ = 2π2/𝑘3 ∆2𝘩(𝑘)/4 × (2π)3𝛿𝐷(𝐤 + 𝐤ʹ) 𝛿𝜆𝜆ʹ, [verification needed]
where the factor of 4 follows from our normalization of the polarization basis in (6.210). In Chapter 8 we willshow how quantum fluctuations during inflation produce a scale-invariant spectrum of primordial GWs, while in Chapter 7, we will explain how these GWs affect the anisotropies in the CMB.
9 For simplicity, we will ignore the photon anisotropic stress. In reality this is only a good approximation because of the coupling to baryons.
10 In a radiation-dominated universe 𝑎ʺ/𝑎 vanishes identically, so that the solution (6.218) doesn't apply. In that case, the the 𝑘𝑛 ≪ 1 limit of (6.217), which again has a decaying mode and a constant mode.
|
|
|





































