|
김관석
|
2024-08-11 11:22:26, 조회수 : 79 |
- Download #1 : BC_2a.jpg (243.7 KB), Download : 0
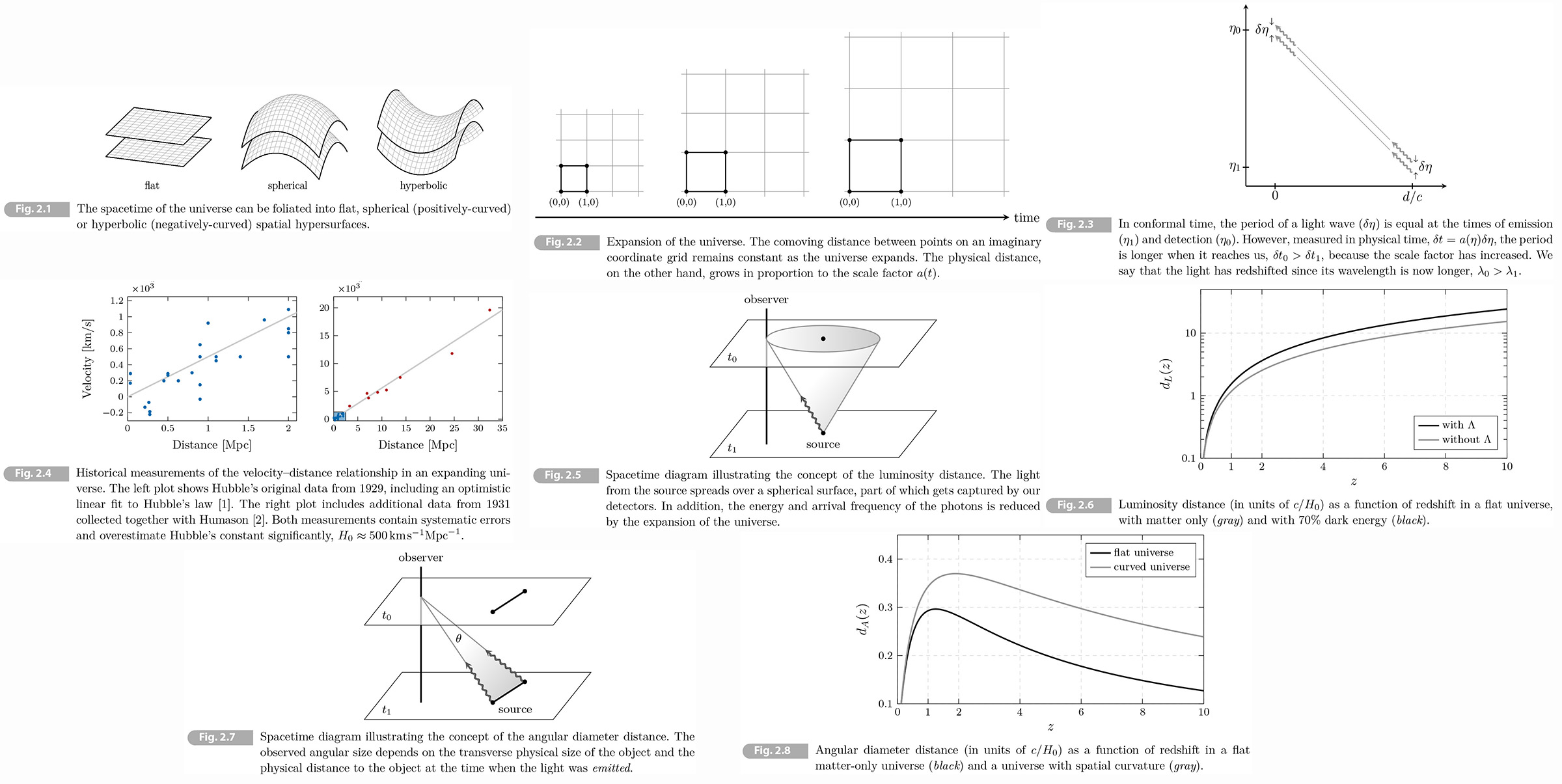
Part I The Homogeneous Universe
2 The Expanding Universe
Our goal in this chapter is to derive, and then solve, the equation governing the evolution of the entire universe.
Fortunately, the coarse-grained properties of the universe are remarkably simple. In particular, when averaged over large distances (larger than 100 Mpc) - the size of the observable universe is about 14,000 Mpc - the universe looks isotropic (the same in all directions). Assuming that we don't live at a special point in space - and that nobody else does either - the observed isotropy then implies that the universe is also homogeneous (the same at every point in space). This leads to a simple mathematical description of the universe because the spacetime geometry takes a very simple form.
Observations of the light from distant galaxies have shown that the universe is expanding. Running this expansion backwards in time, we predict that nearly 14 billion years ago our whole universe was in a hot dense state. The Big Bang theory describes what happened in this fireball., and how it evolved into the universe we see today.
2.1 Geometry
Gravity is a manifestation of geometry of spacetime. To describe the evolution of our universe, we therefore stars by determining its spacetime geometry. This geometry is characterized by a spacetime metric. The large degree of symmetry of the homogeneous universe means that its metric will take a rather simple form
2.1.1 Spacetime and Relativity
The metric is an object that turns coordinate distances into physical distances. In 3-dimensional Euclidean space, the physical distance between two points separated by the infinitesimal coordinate distances 𝑑𝑥, 𝑑𝑦 and 𝑑𝑧 is
(2.1) 𝑑𝓁2 = 𝑑𝑥2 + 𝑑𝑦2 + 𝑑𝑧2 = ∑3𝑖,𝑗=1 𝛿𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗, where (𝑥1, 𝑥2, 𝑥3) = (𝑥, 𝑦, 𝑧).
Here the metric is simply the Kronecker delta 𝛿𝑖𝑗 = diag(1, 1, 1). If we use polar coordinate,
(2.2) 𝑑𝓁2 = 𝑑𝑟2 + 𝑟2𝑑𝜃2 + 𝑟2sin2𝜃𝑑𝜙2 ≡ ∑3𝑖,𝑗=1 𝑔𝑖𝑗 𝑑𝑥𝑖𝑑𝑥𝑗 where (𝑥1, 𝑥2, 𝑥3) = (𝑟, 𝜃, 𝜙).
Here the metric is, a less trivial form, 𝑔𝑖𝑗 = diag(1, 𝑟2, 𝑟2sin2𝜃). Observers can use different coordinate systems will always agree on the physical distance, 𝑑𝑙 which is an invariant. Hence, the metric turns observer-dependent coordinates into invariants.
A fundamental object in relativity is the spacetime metric. It turns observer-dependent spacetime coordinates 𝑥𝜇 = (𝑐𝑡, 𝑥𝑖) into the invariant line element1
(2.3) 𝑑𝑠2 = ∑3𝜇,𝜈=0 𝑔𝜇𝜈𝑑𝑥𝜇𝑑𝑥𝜈 ≡ 𝑔𝜇𝜈𝑑𝑥𝜇𝑑𝑥𝜈. [𝑥0 ≡ 𝑐𝑡 and 𝑥𝑖, 𝑖 = 1, 2, 3]
In special relativity, the spacetime is Minkowski space, 𝓡1,3, whose line element is
(2.4) 𝑑𝑠2 = -𝑐2𝑑𝑡 2 + 𝛿𝑖𝑗 𝑑𝑥𝑖𝑑𝑥𝑗,
so that the metric is simply 𝑔𝜇𝜈 = diag(-1, 1, 1, 1). An important feature of this metric is that the associated spacetime curvature vanishes. In general relativity, on the other hand, the metric depend on the position in spacetime, 𝑔𝜇𝜈(𝑡, 𝐱), in such a way that the spacetime curvature is nontrivial. This spacetime dependence of the metric incorporates the effects of gravity. How the metric varies throughout spacetime is determined by the distribution of matter and energy in the universe.
Indices From special relativity the metric is used to raise and lower indices on 4-vectors (and on general tensors),
(2.5) 𝐴𝜇 = 𝑔𝜇𝜈𝐴𝜈 and 𝐴𝜇 = 𝑔𝜇𝜈𝐴𝜈,
where 𝑔𝜇𝜈 is the inverse metric defined by [𝑔𝜇𝜈 [RE wikipedia Invertible matrix : 𝐀𝐁 = 𝐁𝐀 = 𝐈𝑛 where 𝐈𝑛 denotes 𝑛-by-𝑛 identity matrix.]
(2.6) 𝑔𝜇𝜆𝑔𝜆𝜈 = 𝛿𝜇𝜈 = {1 𝜇 = 𝜈, 0 𝜇 ≠ 𝜈.
4-vectors with a lower index, 𝐴𝜇, are sometimes called covariant to distinguish them from the contravariant 4-vectors, 𝐴𝜇, with an upper index. Covariant and contravariant vectors can be contracted to produce an invariant scalar,
(2.7) 𝑆 ≡ 𝐴 ⋅ 𝐵 = 𝐴𝜇𝐵𝜇 = 𝑔𝜇𝜈𝐴𝜇𝐵𝜇.
The spatial homogeneity and isotropy of the universe mean that it can be represented by a time-ordered sequence of 3-dimensional spatial slices, each of which is homogeneous and isotropic (see Fig. 2.1). The 4-dimensional element can then be written as2
(2.8) 𝑑𝑠2 = -𝑐2𝑑𝑡2 + 𝑎2(𝑡)𝑑𝓁2,
where 𝑑𝓁2 ≡ 𝛾𝑖𝑗(𝑥𝑘)𝑑𝑥𝑖𝑑𝑥𝑗 is the line element on the spatial slices and 𝑎(𝑡) is the scale factor, which describes the expansion of the universe. [RE wikipedia Scale factor : In expanding or contracting universe, 𝑑(𝑡) = 𝑎(𝑡)𝑑0, where 𝑑(𝑡) is the proper distance at time 𝑡, 𝑑0 is the distance at the reference time 𝑡0,𝑑(𝑡0), usually also referred to as comoving distance, and 𝑎(𝑡) is the scale factor. Thus, by definition, 𝑎(𝑡0) = 1]
2.1.2 Symmetric Three-spaces
Homogeneous and isotropic 3-spaces must have constant intrinsic curvature.Then the curvature can be zero, positive or negative.
• Flat space: The simplest possibility is 3-dimensional Euclidean space 𝐸3. This is the space in which parallel lines don't intersect. Its line element is
(2.9) 𝑑𝓁2 = 𝑑𝐱2 = 𝛿𝑖𝑗𝑑𝑥𝑖𝑑𝑥𝑗,
which is clearly invariant under spatial translations 𝑥𝑖 ↦ 𝑥𝑖 + 𝑎𝑖 and rotations 𝑥𝑖 ↦ 𝑅𝑖𝑘𝑥𝑘, with 𝛿𝑖𝑗𝑅𝑖𝑘𝑅𝑗𝑙 = 𝛿𝑘𝑙.[how?]
• Spherical space: The next possibility is a 3-space with constant positive curvature. On such a space, parallel lines will eventually meet. This geometry can be represented as a 3-sphere 𝑆3 embedded in 4-dimensional Euclidean space 𝐸4:
(2.10) 𝑑𝓁2 = 𝑑𝐱2 + 𝑑𝑢2, 𝐱2 + 𝑢2 = 𝑅02,
where 𝑅0 is the radius of the sphere. Homogeneity and isotropy on the surface of the 3-sphere are inherited from the symmetry of the line element under 4-dimensional rotations.
• Hyperbolic space: We can have a 3-space with constant negative curvature. On such a space parallel lines diverge. This geometry can be represented as a hyperboloid 𝐻3 embedded in 4-dimensional Lorentzian space 𝓡1,3:
(2.11) 𝑑𝓁2 = 𝑑𝐱2 - 𝑑𝑢2, 𝐱2 - 𝑢2 = -𝑅02,
where 𝑅02 > 0 is a constant determining the curvature of the hyperboloid. Homogeneity and isotropy of the induced geometry on the hyperboloid are inherited from the symmetry of the line element under 4-dimensional pseudo-rotations - i.e. Lorentz transformations, with 𝑢 playing the role of time.
The line elements of the spherical and hyperbolic cases can be combined as
(2.12) 𝑑𝓁2 = 𝑑𝐱2 ± 𝑑𝑢2, 𝐱2 ± 𝑢2 = ±𝑅02.
The differential of the embedding condition gives 𝑢𝑑𝑢 = ∓𝐱 ⋅ 𝑑𝐱, so that we can eliminate the dependence on the auxiliary coordinate 𝑢 from the line element [𝑑𝑢2/𝑑𝑢 = 𝑑(𝑅02 - 𝐱2)/𝑑𝐱 𝑑𝐱/𝑑𝑢, 𝑢𝑑𝑢 = -𝐱 𝑑𝐱, 𝑑𝑢2 = -(𝐱 𝑑𝐱)2/𝑢2]
(2.13) 𝑑𝓁2 = 𝑑𝐱2 ± (𝐱 ⋅ 𝑑𝐱)2/(𝑅02 ∓ 𝐱2).
Finally, we can unify (2.13) with (2.9) by writing
(2.14) 𝑑𝓁2 = 𝑑𝐱2 + 𝑘 (𝐱 ⋅ 𝑑𝐱)2/(𝑅02 - 𝑘 𝐱2), for 𝑘 ≡ {0 𝐸3, +1 𝑆3, -1 𝐻3.
To make the symmetries of the space more manifest, it is convenient to write the metric in spherical polar coordinates, (𝑟, 𝜃, 𝜙). Using
(2.15) 𝑑𝐱2 = 𝑑𝑟2+ 𝑟2(𝑑𝜃2 + sin2𝜃 𝑑𝜙), 𝐱 ⋅ 𝑑𝐱 = 𝑟𝑑𝑟, 𝐱2 = 𝑟2,
the metric in (2.14) becomes
(2.16) 𝑑𝓁2 = 𝑑𝑟2/(1 - 𝑘𝑟2/𝑅02) + 𝑟2𝑑𝛀2,
where 𝑑𝛀2 ≡ 𝑑𝜃2 + sin2𝜃 𝑑𝜙 is the metric on the unit 2-spheres.
2.1.3 Robertson-Walker Metric
Substituting (2.16) into (2.8), we obtain the Robertson-Walker metric in polar coordinates:
(2.17) 𝑑𝑠2 = -𝑐2𝑑𝑡2 + 𝑎2(𝑡)[𝑑𝑟2/(1 - 𝑘𝑟2/𝑅02) + 𝑟2𝑑𝛀2],
which is sometimes also called the Friedmann-Robertson-Walker (FRW) metric. [RE wikipedia Friedmann-Lemaȋtre-Robertson-Walker metric : in short FLRW or FRW etc.] Notice that the symmetries of the universe have reduced the ten independent components of the spacetime metric 𝑔𝜇𝜈 to a single function of time, the scale factor 𝑎(𝑡), and a constant, the curvature scale 𝑅0.
• First of all, the line element (2.17) has a rescaling symmetry
(2.18) 𝑎 → 𝜆𝑎, 𝑟 → 𝑟/𝜆, 𝑅0 → 𝑅0/𝜆
this means that the geometry of the spacetime stays same if we simultaneously rescale 𝑎, 𝑟 and 𝑅0 by a constant 𝜆 as in (2.18). We can use this freedom to set the scale factor today, at 𝑡 = 𝑡0, to be unity, 𝑎(𝑡0) ≡ 1. The scale 𝑅0 is then the physical curvature scale today, justifying the use of the subscript.
• The coordinate 𝑟 is called a comoving coordinate, which can be changed using the rescaling in (2.18) and hence is not a physical observable. Physical results can only depend on the physical coordinate, 𝑟phys = 𝑎(𝑡)𝑟 (see Fig. 2.2)
Consider a galaxy with a trajectory 𝐫(𝑡) in comoving coordinates and 𝐫phys = 𝑎(𝑡)𝐫 in physical coordinates. The physical velocity of the galaxy is
(2.19) 𝐯phys ≡ 𝑑𝐫phys/𝑑𝑡 = 𝑑𝑎/𝑑𝑡 𝐫 + 𝑎(𝑡) 𝑑𝐫/𝑑𝑡 = 𝐻𝐫phys + 𝐯pec,
where we have introduced the Hubble parameter
(2.20) 𝐻 ≡ ȧ/𝑎.
Here ȧ = 𝑑𝑎/𝑑𝑡. We see that in (2.19) the first term 𝐻𝐫phys is the Hubble flow, which is the velocity of the galaxy resulting from the expansion of space between the origin and 𝐫phys(𝑡). the second term 𝐯pec ≡ 𝑎(𝑡) ṙ, is the peculiar velocity, which is the velocity measured by a "comoving observer" (i.e. an observer who follows the Hubble flow). It describes the motion of galaxy relative to the cosmological rest frame, typically due to the gravitational attraction of other nearby galaxies.
• The complicate 𝑔𝑟𝑟 component of (2.17) may sometimes be redefined, 𝑑𝜒 ≡ 𝑑𝑟/√(1 - 𝑘𝑟2/𝑅02), then
(2.21) 𝑑𝑠2 = -𝑐2𝑑𝑡2 + 𝑎2(𝑡)[𝑑𝜒2 + 𝑆𝑘2(𝜒)𝑑𝛀2],
where
(2.22) 𝑆𝑘(𝜒) = 𝑅0 {sinh(𝜒/𝑅0) 𝑘 = -1, 𝜒/𝑅0 𝑘 = 0, sin(𝜒/𝑅0) 𝑘 = +1.
Note that for for 𝑘 = 0 there is no distinction between 𝑟 and 𝜒. The form of metric in (2.21) will be useful when we define observable distances in section 2.2.3.
• Finally, it is often helpful to introduce conformal time, 𝜂 [RE wikipedia Particle horizon : The conformal time is the amount time that light travel from where we located to the furthest observable distance. 𝜂0 (of today) is not yet actually passed, but it is conceptually meaningful with particle horizon.]
(2.23) 𝑑𝜂 = 𝑑𝑡/𝑎(𝑡) [RE wikipedia Particle horizon : 𝜂 = ∫𝑡0 𝑑𝑡'/𝑎(𝑡')]
so that (2.21) becomes
(2.24) 𝑑𝑠2 = 𝑎2(𝜂)[-𝑐2𝑑𝜂2 + [𝑑𝜒2 + 𝑆𝑘2(𝜒)𝑑𝛀2].
We see that the metric has now factorized into a static part and a time-dependent conformal factor 𝑎(𝜂). This is convenient for studying the propagation of light, for which 𝑑𝑠2 = 0. As we will see in section 2.3.6, going to conformal time also will be useful change of variables for certain exact solutions to the Einstein equations.
2.2 Kinematics
Having found the metric of the expanding universe, we now want to determine how particles evolve in the spacetime. It is an essential feature of general relativity that freely falling particles in a curved spacetime moving along geodesics. Some basic facts about geodesic motion in GR will be introduced and then it be applied to FRW spacetime. [RE Appendix A for more detail]
2.2.1 Geodesics
Let us first look at simpler problem of a free particle in 2-dimensional Euclidean space.
Curvilinear coordinates
In the absence of any forces, Newton's law simply reads 𝑑2𝐱/𝑑𝑡2 = 0 [ẍ = 0], which in Cartesian coordinates 𝑥𝑖 = (𝑥, 𝑦) becomes
(2.25) 𝑑2𝑥𝑖/𝑑𝑡2 = 0.
In a general coordinate system, however, ẍ = 0 does not have to imply 𝑑2𝑥𝑖/𝑑𝑡2 = 0. For example in the polar coordinate (𝑟, ϕ), using 𝑥 = 𝑟 cos ϕ and 𝑦 = 𝑟 sin ϕ, the equation of motion in (2.25) imply
(2.26) 0 = ẍ = ϔ cos ϕ - 2 sin ϕ ṙ ᾠ - 𝑟 cos ϕ ᾠ2 - 𝑟 sin ϕ ᾥ, 0 = ÿ = ϔ sin ϕ + 2 cos ϕ ṙ ᾠ - 𝑟 sin ϕ ᾠ2 + 𝑟 cos ϕ ᾥ.
Solving this for ϔ and ᾥ, we find
(2.27) ϔ = 𝑟 ᾠ2, ᾥ = - 2/𝑟 ṙ ᾠ.
we see that ϔ ≠ 0 and ᾢ ≠ 0. The reason is simply that in polar coordinates the basis vector ȓ and ῷ vary in the plane. To keep ẍ = 0, the coordinates must then satisfy (2.27).
Exercise 2.1 Show that the equations (2.27) can also be derive the Lagrangian of the free particle
(2.28) 𝐿 = 𝑚/2 (ṙ2 + 𝑟2ᾡ2). Using Euler-Lagrange equation, 𝑑/𝑑𝑡 (∂𝐿/∂ẋ𝑘) = ∂𝐿/∂𝑥𝑘
[Solution] Let us start, 𝑑/𝑑𝑡 (∂𝐿/∂ṙ) = 𝑑/𝑑𝑡 𝑚/2 (2 ṙ + 0) = 𝑚ϔ, ∂𝐿/∂𝑟 = 𝑚/2 (0 + 2 𝑟ᾡ2) = 𝑚𝑟ᾡ2. ⇒ ϔ = 𝑟ᾡ2. Similarly, 𝑑/𝑑𝑡 (∂𝐿/∂ᾡ) = 𝑑/𝑑𝑡 𝑚/2 (0 + 2 𝑟2ᾡ) = 𝑚 𝑑/𝑑𝑡 𝑟2ᾡ = 𝑚 (𝑑𝑟2/𝑑𝑡 ᾡ + 𝑟2𝑑ᾡ/𝑑𝑡) = 𝑚 (2𝑟 ṙ ᾡ + 𝑟2 ᾥ), ∂𝐿/∂ϕ = 𝑚/2 (0 + 0) = 0, 2𝑟 ṙ ᾡ + 𝑟2 ᾥ = 0. ⇒ ᾥ = -2/𝑟 ṙ ᾡ. ▮
To derive the equation of motion in an arbitrary coordinate system, which metric 𝑔𝑖𝑗 ≠ 𝛿𝑖𝑗, we start from the Lagrangian [RE wikipedia Lagrangian
mechanics: 𝐿 = 𝑇 - 𝑉, where 𝑇 and 𝑉 are kinetic and potential energy of the system, respectively.]
(2.29) 𝐿 = 𝑚/2 𝑔𝑖𝑗(𝑥𝑘) ẋ𝑖 ẋ𝑗.
Substituting this into the Euler-Lagrangian equation, we find
(2.30) 𝑑2𝑥𝑖/𝑑𝑡2 = -𝛤𝑖𝑎𝑏 𝑑𝑥𝑎/𝑑𝑡 𝑑𝑥𝑏/𝑑𝑡,
where we have introduced the Christoffel symbol
(2.31) 𝛤𝑖𝑎𝑏 ≡ 1/2 𝑔𝑖𝑗(∂𝑎𝑔𝑖𝑏 + ∂𝑏𝑔𝑗𝑎 - ∂𝑗𝑔𝑎𝑏), with ∂𝑗 ≡ ∂/∂𝑥𝑗.
Derivation The Euler-Lagrangian equation is
(2.32) 𝑑/𝑑𝑡 (∂𝐿/∂ẋ𝑘) = ∂𝐿/∂𝑥𝑘.
The mass 𝑚 will be cancel on both side. The left-hand side of (2.32) then becomes [∂𝐿/∂ẋ𝑘 = 1/2 ∂(𝑔𝑖𝑗ẋ𝑖𝑗)/∂ẋ𝑘 = 1/2 (𝑔𝑖𝑘ẋ𝑖 + 𝑔𝑘𝑗ẋ𝑗) = 𝑔𝑖𝑘ẋ𝑖]
(2.33) 𝑑/𝑑𝑡 (∂𝐿/∂ẋ𝑘) = 𝑑/𝑑𝑡 (𝑔𝑖𝑘ẋ𝑖) = 𝑔𝑖𝑘ẍ𝑖 + 𝑑𝑥𝑗/𝑑𝑡 ∂𝑔𝑖𝑘/∂𝑥𝑗 ẋ𝑖 = 𝑔𝑖𝑘ẍ𝑖 + ∂𝑗𝑔𝑖𝑘 ẋ𝑖 ẋ𝑗 = 𝑔𝑖𝑘ẍ𝑖 + 1/2 (∂𝑖𝑔𝑗𝑘 + ∂𝑗𝑔𝑖𝑘) ẋ𝑖 ẋ𝑗,
while the right-hand side is
(2.34) ∂𝐿/∂𝑥𝑘 = 1/2 ∂𝑘𝑔𝑖𝑗 ẋ𝑖 ẋ𝑗.
Combing (2.33) and (2.34) then gives
(2.35) 𝑔𝑖𝑘ẍ𝑖 = -1/2 (∂𝑖𝑔𝑗𝑘 + ∂𝑗𝑔𝑖𝑘 - ∂𝑘𝑔𝑖𝑗) ẋ𝑖 ẋ𝑗
Multiplying both sides by 𝑔𝑙𝑘, and using 𝑔𝑙𝑘 𝑔𝑘𝑖 = 𝛿𝑙𝑖, we get
(2.36) ẍ𝑙 = -1/2 𝑔𝑙𝑘(∂𝑖𝑔𝑗𝑘 + ∂𝑗𝑔𝑖𝑘 - ∂𝑘𝑔𝑖𝑗) ẋ𝑖 ẋ𝑗 ≡ -𝛤𝑙𝑖𝑗,
which is the desired result (2.30). ▮
The equation of motion of a massive particle in general relativity will take a similar form as (2.30). However, i this case, the term involving the Christoffel symbol cannot be removed by going to Cartesian coordinate, but is a physical manifestation of the spacetime curvature.
Curved spacetime
For massive particles, a geodesic is the timelike curve 𝑥𝜇(𝜏) which extremises the proper time 𝛥𝜏 between two points in the spacetime.3 This extremal path satisfies the following geodesic equation [RE Appendix A]
(2.37) 𝑑2𝑥𝜇/𝑑𝜏2 = -𝛤𝑖𝑎𝑏 𝑑𝑥𝑎/𝑑𝜏 𝑑𝑥𝑏/𝑑𝜏, [RE wikipedia Four-velocity : 𝑑𝑡 = 𝛾(𝑢)𝑑𝜏, 𝛾(𝑢) = 1/√(1 - 𝑢2/𝑐2), 𝑢 = ∣𝐮∣ = √[(𝑢1)2 + (𝑢2)2 + (𝑢3)2], 𝐔 = (𝑈0, 𝑈1, 𝑈2, 𝑈3), 𝑥0 = 𝑐𝑡, 𝑈0 = 𝑑𝑥0/𝑑𝜏 = 𝑐 𝑑𝑡/𝑑𝜏 = 𝑐𝛾(𝑢) 𝑈𝑖 = 𝑑𝑥𝑖/𝑑𝜏 = 𝑑𝑥𝑖/𝑑𝑡 𝑑𝑡/𝑑𝜏 = 𝛾(𝑢)𝑢𝑖.]
where the Christoffel symbol is
(2.38) 𝛤𝜇𝛼𝛽 = 1/2 𝑔𝜇𝜆(∂𝛼𝑔𝛽𝜆 + ∂𝛽𝑔𝛼𝜆 - ∂𝜆𝑔𝛼𝛽), with ∂𝛼 ≡ ∂/∂𝑥𝛼.
Notice the similarity between (2.37) and (2.30).
It will be convenient to write the geodesic equation in terms of the 4-momentum of the particle
(2.39) 𝛲𝜇 ≡ 𝑚 𝑑𝑥𝜇/𝑑𝜏. [RE wikipedia Four momentum : 𝑝𝜇 = 𝑚𝑢𝜇]
Using the chain rule, we have
(2.40) [𝑚 𝑑2𝑥𝜇/𝑑𝜏2 =] 𝑑/𝑑𝜏 𝛲𝜇(𝑥𝛼(𝜏)) = 𝑑𝑥𝛼/𝑑𝜏 ∂𝛲𝜇/∂𝑥𝛼 = 𝛲𝛼/𝑚 ∂𝛲𝜇/∂𝑥𝛼,
so that (2.37) becomes
(2.41) [𝑚2 𝑑2𝑥𝜇/𝑑𝜏2 =] 𝛲𝛼 ∂𝛲𝜇/∂𝑥𝛼 = -𝛤𝜇𝛼𝛽 𝛲𝛼𝛲𝛽.
Rearranging the expression, we can also write
(2.42) 𝛲𝛼(∂𝛼𝛲𝛼 + 𝛤𝜇𝛼𝛽𝛲𝛽) = 0.
The term in brackets is so-called covariant derivative of 4-vector 𝛲𝜇 which we denote by 𝛻𝛼𝛲𝜇 ≡ ∂𝛼𝛲𝛼 + 𝛤𝜇𝛼𝛽𝛲𝛽. So we can write:
(2.43) 𝛲𝛼𝛻𝛼𝛲𝜇 = 0.
The form of the geodesic equation in (2.43) is particularly convenient because it also applies to massless particles.If we interpret 𝛲𝜇 ≡ 𝑚 𝑑𝑥𝜇/𝑑𝜆 as the 4-momentum of a massless particle, where 𝜆 now parameterizes the curve 𝑥𝜇(𝜆). Accepting that the geodesic equation (2.43) is valid for both massive and massless particles, we will apply it to particles in the FRW spacetime.
Free particles in FRW
To evaluate the right-hand side of (2.41), we need the Christoffel symbols for the for the FRW metric,
(2.44) 𝑑𝑠2 = -𝑐2𝑑𝑡2 + 𝑎2(𝑡) 𝛾𝑖𝑗 𝑑𝑥𝑗𝑑𝑥𝑖
where the form of the spatial metric 𝛾𝑖𝑗 depends on our choice of spatial coordinates and on the curvature of the spatial slices. Substituting 𝑔𝜇𝜈 = diag(-1, 𝑎2(𝑡) 𝛾𝑖𝑗) into the definition (2.38), it is straightforward to compute the Christoffel symbols. Note that all Christoffel symbols with two time[-0] indices vanish, i.e. 𝛤𝜇00 = 𝛤00𝛽 and 𝛤𝜇𝛼𝛽 = 𝛤𝜇𝛽𝛼. The only nonzero components are
(2.45) 𝛤0𝑖𝑗 = 𝑐-1𝑎ȧ𝛾𝑖𝑗, 𝛤𝑖0𝑗 = 𝑐-1ȧ/𝑎𝛿𝑖𝑗, 𝛤𝑖𝑗𝑘 = 1/2 𝛾𝑖𝑙(∂𝑗𝛾𝑘𝑙 + ∂𝑘𝛾𝑗𝑙 - ∂𝑙𝛾𝑗𝑘).
Example Let us derive 𝛤0𝛼𝛽 for metric (2.44).
(2.46) 𝛤0𝛼𝛽 = 1/2 𝑔0𝜆(∂𝛼𝑔𝛽𝜆 + ∂𝛽𝑔𝛼𝜆 - ∂𝜆𝑔𝛼𝛽).
The factor 𝑔0𝜆 vanish unless 𝜆 = 0, 𝑔00 = -1. Hence we have
(2.47) 𝛤0𝛼𝛽 = -1/2 (∂𝛼𝑔𝛽0 + ∂𝛽𝑔𝛼0 - ∂0𝑔𝛼𝛽).
The first two terms reduced to derivatives of 𝑔00 and 𝑔00 = -1, so we have
(2.48) 𝛤0𝛼𝛽 = 1/2 ∂0𝑔𝛼𝛽.
∂0 means ∂/∂𝑥0 and 𝑥0 ≡ 𝑐𝑡 so ∂0 = 𝑐-1∂𝑡. The derivative is nonzero if 𝑔𝑖𝑗 = 𝑎2𝛾𝑖𝑗. In that case we find
(2.49) 𝛤0𝛼𝛽 = 1/2 𝑐-1∂/∂𝑡 𝑎2𝛾𝑖𝑗 = 1/2 𝑐-1∂/∂𝑎 𝑎2𝛾𝑖𝑗 ∂𝑎/∂𝑡 = 𝑐-1𝑎ȧ𝛾𝑖𝑗. ▮
Exercise 2.2 Derive 𝛤𝑖0𝑗 and 𝛤𝑖𝑗𝑘 for metric (2.44).
[Solution] 𝛤𝑖0𝑗 = 1/2 𝑔𝑖𝜆(∂0𝑔𝑗𝜆 + ∂𝑗𝑔0𝜆 - ∂𝜆𝑔0𝑗), But 𝑔0𝑗 = 𝑔0𝜆 = 0, 𝛤𝑖0𝑗 = 1/2 𝑔𝑖𝜆∂0𝑔𝑗𝜆,
In FRW metric, 𝑔𝑖𝜆 = 1/𝑎2 𝛾𝑖𝜆. And since ∂0 = 𝑐-1 ∂𝑡 and 𝑔𝑗𝜆 = 𝑎2𝛾𝑗𝜆, ∂0𝑔𝑗𝜆 = 𝑐-1 2𝑎 ȧ 𝛾𝑖𝜆. So we have
𝛤𝑖0𝑗 = 1/2 1/𝑎2 𝛾𝑖𝜆 𝑐-1 2𝑎 ȧ 𝛾𝑖𝜆 = 𝑐-1 ȧ/𝑎 𝛿𝑖𝑗. ▮
𝛤𝑖𝑗𝑘 = 1/2 𝑔𝑖𝑙(∂𝑗𝑔𝑘𝑙 + ∂𝑘𝑔𝑗𝑙 - ∂𝑙𝑔𝑗𝑘),
Since 𝑔𝑖𝑙 = 1/𝑎2 𝛾𝑖𝑙 and the derivative is nonzero, if 𝑗, 𝑘 and 𝑙 are spatial indices, 𝑔𝑗𝑙 = 𝑎2 𝛾𝑗𝑙, 𝑔𝑘𝑙 = 𝑎2 𝛾𝑘𝑙 and 𝑔𝑗𝑘 = 𝑎2 𝛾𝑗𝑘 respectively. So we have
𝛤𝑖𝑗𝑘 = 1/2 1/𝑎2 𝛾𝑖𝑙(∂𝑗 𝑎2 𝛾𝑘𝑙 + ∂𝑘 𝑎2 𝛾𝑗𝑙 - ∂𝑙 𝑎2 𝛾𝑗𝑘) = 1/2 𝛾𝑖𝑙(∂𝑗 𝛾𝑘𝑙 + ∂𝑘 𝛾𝑗𝑙 - ∂𝑙 𝛾𝑗𝑘). ▮
The case of massless particle (like photons) will be specialized. The left-hand side of (2.41) can be written when 𝛼 = 0
(2.50) 𝛲0 ∂𝛲𝜇/∂𝑥0 = 𝛲0/𝑐 𝑑𝛲𝜇/𝑑𝑡, [Notice that
𝑥0 ≡ 𝑐𝑡 and ∂0 = 𝑐-1∂𝑡.]
(2.51) 𝛲0/𝑐 𝑑𝛲𝜇/𝑑𝑡 = -𝛤𝜇𝛼𝛽 𝛲𝛼𝛲𝛽.
Let us consider the 𝜇 = 0 component of the equation, Then the right term is -𝛤0𝑖𝑗 𝛲𝑖𝛲𝑗. Using 𝛲0 = 𝐸/𝑐 and 𝛤0𝑖𝑗 = 𝑐-1𝑎ȧ𝛾𝑖𝑗 then we find, [RE wjkipedia photon : 𝐸2 = 𝑝2𝑐2 + 𝑚2𝑐4, if 𝑚 = 0, then 𝐸 = 𝑝𝑐; Four-momentum : In special relativity, 𝑝𝜇 = (𝐸/𝑐, 𝑝𝑥, 𝑝𝑦, 𝑝𝑧),]
(2.52) 𝐸/𝑐3 𝑑𝐸/𝑑𝑡 = -𝑐-1𝑎ȧ𝛾𝑖𝑗𝛲𝑖𝛲𝑗.
For massless particles, the 4-momentum 𝛲𝜇 = (𝐸/𝑐, 𝛲𝑖) obey the constraint
(2.53) 𝑔𝜇𝜈𝛲𝑖𝛲𝜈 = -𝑐2𝐸2 + 𝑎2𝛾𝑖𝑗𝛲𝑖𝛲𝑗 = 0. [Notice that lightlike 𝑑𝑠2 = 0.]
This allow us to write (2.51) as
(2.54) 1/𝐸 𝑑𝐸/𝑑𝑡 = -ȧ/𝑎, [∫ (1/𝐸 𝑑𝐸/𝑑𝑡) 𝑑𝑡 = log(𝐸) + const; ∫ (-1/𝑎 𝑑𝑎/𝑑𝑡) 𝑑𝑡 = log(𝑎-1) + const ⇒ 𝐸 ∝𝑎-1]
which implies that the energy of a massless particle decays with the expansion of the universe, 𝐸 ∝𝑎-1.
Exercise 2.3 Repeating the analysis for massive particle, with
(2.55) 𝑔𝜇𝜈𝑃𝜇𝑃𝜈 = -𝑚2𝑐2
show that the physical 3-momentum, defined as 𝑝2 ≡ 𝑔𝑖𝑗𝑃𝑖𝑃𝑗, satisfies 𝑝 ∝𝑎-1. Show that the momentum can be written as
(2.56) 𝑝 = 𝑚𝑣/√(1 - 𝑣2/𝑐2).
where 𝑣2 ≡ 𝑔𝑖𝑗ẋ𝑖ẋ𝑗 is the physical peculiar velocity. Since 𝑝 ∝𝑎-1, freely falling particles will therefore converge onto the Hubble flow.
[Solution] In the text, we have shown that the geodesic equation of a particle with 4-momentum 𝑃𝜇 = (𝐸/𝑐, 𝑃𝑖) can be written as
𝐸/𝑐3 𝑑𝐸/𝑑𝑡 = -𝑐-1 ȧ/𝑎 𝑝2,
𝑔𝜇𝜈𝑃𝜇𝑃𝜈 = -𝑐-2𝐸2 + 𝑝2 = -𝑚2𝑐2 [Take a time derivative the both side of the equation and arrange them.]
𝐸/𝑐3 𝑑𝐸/𝑑𝑡 = 𝑝/𝑐 𝑑𝑝/𝑑𝑡 = -𝑐-1 ȧ/𝑎 𝑝2,
ṗ/𝑝 = -ȧ/𝑎.
The physical 3-momentum of a massive particle therefore decreases as 𝑝 ∝𝑎-1.
From the definition of 4-momentum of a massive particle, we get
𝑃𝑖 ≡ 𝑚 𝑑𝑥𝑖/𝑑𝜏 = 𝑚 𝑑𝑥/𝑑𝜏 ẋ𝑖 = 𝑚ẋ𝑖/√(1 - 𝑔𝑖𝑗ẋ𝑖ẋ𝑗/𝑐2) = 𝑚ẋ𝑖/√(1 - 𝑣2/𝑐2)
Now we have (2.56), 𝑝 = 𝑚𝑣/√(1 - 𝑣2/𝑐2).
Since 𝑝 decreases with the expansion of the universe, so will 𝑣, showing that freely falling particles will converge onto the Hubble flow. ▮
2.2.2 Redshift
The light emitted by a distant galaxy can be interpreted either quantum mechanically as freely-propagating photons or classically as propagating electromagnetic waves. To analyze the observation correctly, we need to take into account that wavelength of light gets stretched (or equivalently, the photons lose energy) by the expansion of the universe.
Recall wavelength 𝜆 = 𝘩/𝛦, where 𝛦 is photon energy and 𝘩 is Planck's constant. Since the energy of photon evolves as 𝐸 ∝𝑎-1, the wavelength scales as 𝜆 ∝𝑎. Light emitted at a time 𝑡1 with 𝜆1 will be observed at a later time 𝑡0 with a larger wavelength
(2.57) 𝜆1 = 𝑎(𝑡0)/𝑎(𝑡1) 𝜆0.
This increased wavelength is called redshift, since red light has a longer wavelength than blue light.
The same result can be derived by the classical method. Consider a galaxy at a fixed comoving distance 𝑑. Since the spacetime is isotropic, we can choose coordinates for which light travels in the radial direction with 𝜃 = 𝜙 =const. Then the evolution is determined by a 2-dimensional line element.
(2.57) 𝑑𝑠2 = 𝑎2(𝜂)[-𝑐2𝑑𝜂2 + 𝑑𝜒2].
Since photons travel along null geodesics, with 𝑑𝑠2 = 0, their path is
(2.58) 𝛥𝜒(𝜂) = ±𝑐𝛥𝜂,
where the plus sign corresponds to outgoing photons and its minus sign to incoming photons. This shows the main benefit of working with conformal time: light rays correspond to straight lines in the 𝜒-𝜂 coordinates. Moreover comoving distance to a source is simply equal to the difference in conformal time between the moments of being emitted and received.
At a time 𝜂1, the galaxy emits a signal of a short conformal duration 𝛿𝜂 (see Fig. 2.3).The light arrives at our telescopes at time 𝜂0 = 𝜂1 + 𝑑/𝑐. The conformal duration signal measured by the detector is the same as at the source, but the physical time intervals are different at the points of emission and detection.
(2.60) 𝛿𝑡1 = 𝑎(𝜂1)𝛿𝜂 and 𝛿𝑡0 = 𝑎(𝜂0)𝛿𝜂.
If 𝛿𝑡 is the period of the light wave, then the light is emitted with wavelength 𝜆1 = 𝑐𝛿𝑡1, but is observed with wavelength 𝜆0 = 𝑐𝛿𝑡0, so that
(2.61) 𝜆0/𝜆1 = 𝑎(𝜂0)/𝑎(𝜂1),
which agree with the result in (2.57).
It is conventional to define the redshift as the fractional shift in the wavelength:
(2.62) 𝑧 ≡ (𝜆0 - 𝜆1)/𝜆1.
By comparing the observed wavelengths with those measured in a laboratory on Earth, we determine the redshift. Using (2.61), and setting 𝑎(𝑡0) ≡ 1, we can write the redshift parameter as
(2.63) 1 + 𝑧 = 1/𝑎(𝑡1)
For example, a galaxy at 𝑧 = 1 emitted the observed light when the universe was half its current size. The CMB photons were released at 𝑧 = 1100 and the first galaxies formed around redshift 𝑧 ∼ 10.
For nearby sources at 𝑧 < 1, we can expand the scale factor in a power series around 𝑡0:
(2.64) 𝑎(𝑡1) = 1 + (𝑡1 - 𝑡0)𝐻0 + ∙ ∙ ∙ ,
where 𝑡0 - 𝑡1 is the look-back time and 𝐻0 is the Hubble constant
(2.65) 𝐻0 ≡ ȧ(𝑡0)/𝑎(𝑡0).
Equation (2.63) then gives 𝑧 = 𝐻0(𝑡0 - 𝑡1) + ∙ ∙ ∙ , For close objects, 𝑡0 - 𝑡1 is simply equal to 𝑑/𝑐, so that the redshift increase linearly with distance. This linear relation is called the Hubble-Lemaitre law. In terms of the recession speed of the object, 𝑣 = 𝑐𝑧, it reads
(2.66) 𝑣 = 𝑐𝑧 ≈ 𝐻0𝑑.
Hubble's original measurement of the velocity-distance relations of galaxies are shown in Fig. 2.4. For distant objects (𝑧 > 1), we have to be more careful about the meaning of "distance".
2.2.3 Distances
Measuring distances in cosmology is notoriously difficult. The distances appearing in the metric are not observable. Even the physical distance 𝑑phs = 𝑎(𝑡)𝜒 cannot be observed because it is the distance between separated events at a fixed time. A more practical definition of "distance" must tke into account that the universe is expanding and that it takes light a finite amount of time to reach us.
Luminosity distance
An important way to measure distances in cosmology uses standard candles. These are objects of known intrinsic brightness, so that observed brightnesses can be used to determine their distances.
Hubble used Cepheids to discover the expansion of the universe. These are stars whose brightness vary periodically. The observed periods were found to be correlated with the intrinsic brightness of stars. By measuring the time variation of Cepheids, astronomers can infer their absolute brightness and then use their observed brightness to infer their distances. To measure larger distances we need brighter sources. These are provided by type Ia supernovae-stellar explosions that arise when a white dwarf accretes too much matter from a companion star. Supernovae are rare (roughly a few per century in a typical galaxy), but outshine all stars in the host galaxy and can therefore be seen out to enormous distances. By observing many galaxies, astronomers can then measure a large number of supernovae.
The supernovae explosions occur at relatively precise moment - when the mass of the white dwarf exceeds the Chandrasekar limit - and therefore have fixed brightness. Residual variations of their brightness can be corrected for phenomenologically. The use of supernovae as standard candles have been instrumental in the discovery of the acceleration of the universe and they continue to play an important role in observational cosmology.5
Let us assume that we have identified n astronomical object with a known luminosity 𝐿 (= energy emitted per unit time). The observed flux 𝐹 (= energy per unit time per receiving area) can then be used to infer its (luminosity) distance. Our task is to determine the relation between 𝐿 and 𝐹 in an expanding universe.
Consider a source at a redshift 𝑧. The comoving distance to the object is
(2.67) 𝜒(𝑧) = ∫𝑡0𝑡1 𝑑𝑡/𝑎(𝑡) = ∫𝑧0 𝑑𝑧/𝐻(𝑧),
where the redshift evolution of the Hubble parameter, 𝐻(𝑧), depends on the matter content of the universe (see Section 2.3). We assume That the source emits radiation isotropically (see Fig. 2.5). In a static Euclidean space, the energy would then spread uniformly over a sphere of area 4π𝜒2, and the fraction going through an area 𝐴 (e.g. the collecting area of a telescope) is 𝐴/4π𝜒2. The relation between the absolute luminosity and the observed flux would then be
(2.68) 𝐹 = 𝐿/4π𝜒2 (static space).
In an expanding spacetime, this result is modified for three reasons:
1. When the light reaches the Earth, at time 𝑡0, a sphere with radius 𝜒 has and area
(2.69) 4π𝑎2(𝑡0)𝑑2𝑀,
where 𝑑𝑀 ≡ 𝑆𝑘 (𝜒) is the"metric distance" defined in (2.22). In a curved space, the metric distance 𝑑𝑀 differs from the radius 𝜒.
2. THe arrive of the photons is smaller than the rate at which they are emitted at the source by a factor of a(𝑡1)/
a(𝑡0) = 1/(1 + 𝑧); cf. Fig. 2.3. This reduces the observed flux by the same factor.
3. The energy 𝐸0 = 𝘩𝑓0 of the observed photons is less than the energy 𝐸1 = 𝘩𝑓1 by the same redshift factor 1/(1 + 𝑧). This lowers the observed flux by another factor of 1/(1 + 𝑧).
Hence, the correct formula is
(2.70) 𝐹 = 𝐿/4π(𝑡0)𝑑2𝑀(1 + 𝑧)2 ≡ 𝐿/4π𝑑2𝐿 .
In the second equality, we have defined the luminosity distance, 𝑑𝐿, so that the relation between luminosity, flux and luminosity istance is the same as in (2.68).
Hence, we find
(2.71) 𝑑𝐿(𝑧) = (1 + 𝑧)𝑑𝑀(𝑧) ,
where the metric distance for an object with redshift 𝑧 depends on the cosmological parameters. Figure 2.6 shows the luminosity distance as a function of redshift in a universe with and without dark energy. WE see that the luminosity distance out to a fixed redshift is larger in a dark energy-dominated universe than in a matter-only universe.
For objects at low redshifts (𝑧 <1), we can define perturbative corrections to Hubble's law (2.66). We first extend the Taylor expression of 𝑎(𝑡) in (2.64) to higher order in the look-back time
(2.72) 𝑎(𝑡) = 1 + 𝐻0(𝑡 - 𝑡0) - 1/2 𝑞0𝐻02(𝑡 - 𝑡0)2 + ∙ ∙ ∙ ,
where we have defined
(2.73) 𝑞0 ≡ -ä/𝑎𝐻2∣𝑡=𝑡0.
The parameter 𝑞0 was named as the deceleration parameter. [Re wikipedia Accelerating expansion of the universe: It was before the accelerated expansion of the universe was discovered in 1998.] Today, we know that it is negative, 𝑞0 ≈ -0.5, and hence measures the acceleration of the universe. Substituting (2.72) into (2.63), we obtain the redshift as a function of the look-back time
(2.74) 𝑧 = 1/𝑎(𝑡1) - 1 = 𝐻0(𝑡0 - 𝑡1) +1/2 (2 + 𝑞0)𝐻02(𝑡0 - 𝑡1)2 + ∙ ∙ ∙ .
This can be inverted to give
(2.75) 𝐻0(𝑡0 = 𝑧 - 1/2(2 + 𝑞0)𝑧2 + ∙ ∙ ∙ ,
where the higher-order terms can be ignored as long as 𝑧 < 1. Using (2.72), we can also write the comoving distance in terms of the look-back time and the redshift
(2.76) 𝜒 = 𝑐 ∫𝑡0𝑡1 𝑑𝑡/𝑎(𝑡) = ∫𝑡0𝑡1 𝑑𝑡[1 + 𝐻0(𝑡 - 𝑡0) + ∙ ∙ ∙ ] = 𝑐(𝑡 - 𝑡0) + 1/2 𝐻0/𝑐 𝑐2(𝑡 - 𝑡0)2 + ∙ ∙ ∙ = 𝑐/𝐻0 [𝑧 -1/2(1 + 𝑞0)𝑧2 + ∙ ∙ ∙ ].
Through (2.71) and (2.22), the determines the luminosity distance as a function of the redshift, 𝑑𝐿(𝑧) . For a flat universe, with 𝑆𝑘(𝜒) = 𝜒, the modified Hubble-Lemaître law reads
(2.77) 𝑑𝐿 = 𝑐/𝐻0[𝑧 + 1/2(1 - 𝑞0)𝑧2 + ∙ ∙ ∙ ].
The value of 𝐻0 and 𝑞0 can be extracted by fitting the functional form to the observed 𝑑𝐿(𝑧). The value of 𝑞0 will depend on the energy content of the universe. The results of such a measurement in section 2.4 will be presented.
Measurements of the Hubble constant used to com with very large uncertainties. It therefore become conventional to define
(2.78) 𝐻0 ≡ 100𝘩 km s-1Mpc-1,
where the parameter 𝘩 is used to keep track of how uncertainties in 𝐻0 propagate to the inferred value of other cosmological parameters. The latest supernovae measurements have found
(2.79) 𝘩 = 0.730 ± 0.010 (supernovae),
The Hubble constant cal also be extract from the CMB anisotropy spectrum (see Chapter 7). These observations gives
(2.80) 𝘩 = 0.674 ± 0.005 (CMB).
As we can see, there is currently a statistically significant discrepancy between the two measurements. It is unclear whether this "Hubble tension" is due to an unidentified observational systematic a breakdown in the standard cosmological model.
Angular diameter distance
An alternative way to measure distances is to use standard rulers, i.e. objects of known physical size. The observed angular sizes of such objects then depends on their distances. As we will see in Chapter 7, the typical size of hot and cold spots in the CMB can be predicted theoretically and is therefore a standard ruler. The observed angular size of these spots then determines the distance to the CMB's surface of last-scattering.6
Let us assume that an object is at a comoving distance 𝜒 and that the photons emitted at a time 𝑡1 (see Fig.2.7). The transverse physical size of the object is 𝐷. In static Euclidean space, we would expect its angular size to be
(2.81) 𝛿𝜃 = 𝐷/𝜒 (static space),
where we assumed that 𝛿𝜃 ≪ 1 (in radian), which is true for all cosmological objects. In an expanding universe, this formula becomes
(2.82) 𝛿𝜃 = 𝐷/𝑎(𝑡1)𝑑𝛭 ≡ 𝑑𝛢 (expanding space),
where metric distance 𝑑𝛭 ≡ 𝑆𝑘(𝜒). Notice that the observed angular size, 𝑑𝛢, depends on distance at the time 𝑡1 when the light was emitted. The second equality in (2.82) has defined the angular diameter distance. In terms of the metric distance 𝑑𝛭 and 𝑧, the angular diameter distance is
(2.83) 𝑑𝛢(𝑧) = 𝑑𝛭(𝑧)/(1 + 𝑧).
Fig 2.8 shows the shows that angular diameter distance as a function of redshift in a flat matter-only universe and in a universe with spatial curvature. We see that the angular distance diameter starts decrease around 𝑧𝑚 ∼ 1.5. The spacetime was compressed when the light was emitted and the objects were closer to us than are today. The observed angular size therefore larger.
1 we use Einstein's convention where repeated indices are summed over. Our metric signature will be (-, +, +, +). In this chapter he speed of light will be kept explicit, but in the rest of the book natural units with 𝑐 ≡ 1 will be used.
2 Component 𝑔00 is absorbed into the time coordinate, 𝑑𝑡' ≡ √𝑔00𝑑𝑡. [It's very confusing comment.]
3 Proper time is defined by the relation 𝑐2𝑑𝜏2 = -𝑑𝑠2. The relativistic action of a massive particle is 𝑆 = -𝑚𝑐2 ∫ 𝑑𝜏, so extremising the proper time between the events is equivalent to extremising the action.
4 We have used the parametrization (2.24) for the radial coordinate 𝜒, so that (2.57) is conformal to a 2-dimensional Minkowski space and the curvature scale 𝑅0 of the 3-dimensional spatial slices is absorbed into the definition of 𝜒.
5 In the future, gravitational waves (GWs) will allow for robust measurements of luminosity distances using so-called standard sirens. The observed waveforms of GW signals determine the parameters of sources (like the masses of the objects in a binary system) and general relativity then predicts the emitted GW power. Comparing this to the observed GW amplitude provides a clean measurement of the luminosity distance.
6We observed the CMB at a fixed moment in t |
|
|
