|
김관석
|
2025-03-24 15:05:39, 조회수 : 24 |
- Download #1 : BC_Sa.jpg (109.8 KB), Download : 0

2 The Expanding Universe: Selected Problems
2.1 Robertson-Walker metric
In this problem, we will be guided through an alternative derivation of the Robertson-walker metric:
1. Explain why the most general metric for a homogeneous and isotropic universe is
(2.1.1) d𝑠2 = -d𝑡2 + 𝑎(𝑡)𝛾𝑖𝑗(𝐱)d𝑥𝑖d𝑥𝑗,
where we have set 𝑐 ≡ 1. In particular, explain why 𝑔00 = -1 and 𝑔0𝑖 = 0.
[Solution] Since 𝑔00 is the time coordinate in Minkowski space, 𝑔00 = -1. Because there is no preferred direction, 𝑔0𝑖 should be zero. ▮
2.2 Geodesic from a Lagrangian
In Appendix A, we derive the geodesic equation from the relativistic action of a point particle. In this problem we will discover a simpler way to obtain the same result.
1. Consider the "Lagrangian"
(2.2.1a) 𝓛 ≡ -𝑔𝜇𝜈ẋ𝜇ẋ𝜈,
where ẋ𝜇 ≡ d𝑥𝜇/d𝜆, for a general parameter 𝜆. Show the Euler-Lagrange equation
(2.2.1b) d𝑥/d𝜆 (∂𝓛/∂ẋ𝜇) = ∂𝓛/∂𝑥𝜇
leads to the geodesic equation.
[Solution] We adjust the Lagrangian as
(a) 𝓛 = -𝑔𝛼𝛽ẋ𝛼ẋ𝛽
Then the Lagrangian's derivatives are
(b) ∂𝓛/∂ẋ𝜇 = -2𝑔𝜇𝛼ẋ𝛼, ∂𝓛/∂𝑥𝜇 = -∂𝜇𝑔𝛼𝛽ẋ𝛼ẋ𝛽.
The Euler-Lagrangian equation becomes
(c) d𝑥/d𝜆 (∂𝓛/∂ẋ𝜇) = ∂𝓛/∂𝑥𝜇 ⇒ 2∂𝛽𝑔𝜇𝛼ẋ𝛼ẋ𝛽 + 2𝑔𝜇𝛼ẍ𝛼 = ∂𝜇𝑔𝛼𝛽ẋ𝛼ẋ𝛽. ⇒ 2𝑔𝜇𝛼ẍ𝛼 = (∂𝜇𝑔𝛼𝛽 - ∂𝛽𝑔𝜇𝛼 - ∂𝛼𝑔𝜇𝛽) ẋ𝛼ẋ𝛽.
Multiplying both sides with 𝑔𝛾𝜇 and arranging them, we get the geodesic equation as follows
(d) ẍ𝛾 = -1/2 𝑔𝛾𝜇 (∂𝛽𝑔𝜇𝛼 + ∂𝛼𝑔𝜇𝛽 - ∂𝜇𝑔𝛼𝛽) ẋ𝛼ẋ𝛽 = -𝛤𝛾𝛼𝛽ẋ𝛼ẋ𝛽. ▮
2. If 𝓛 has no explicit dependence on 𝜆, then ∂𝓛/∂𝜆 = 0. Show that this implies that the "Hamiltonian" is a constant along the geodesics:
(2.2.2) 𝓗 ≡ 𝓛 - ∂𝓛/∂ẋ𝜇 ẋ𝜇 = 𝑔𝜇𝜈ẋ𝜇ẋ𝜈.
For massive particles, we can set 𝜆 equal to the proper time 𝜏, and the constraint becomes 𝑔𝜇𝜈ẋ𝜇ẋ𝜈 = -1. A nice feature of the Lagrangian method is also applies to massless particles, in which case we must have 𝑔𝜇𝜈ẋ𝜇ẋ𝜈 = 0.
[Solution] The total derivative of the Lagrangian is
(a) d𝓛/d𝜆 = ∂𝓛/∂𝜆 + d𝑥𝜇/d𝜆 ∂𝓛/∂𝑥𝜇 + dẋ𝜇/d𝜆 ∂𝓛/∂ẋ𝜇.
Since ∂𝓛/∂𝜆 = 0 and using 2.2.1 (c) for ∂𝓛/∂𝑥𝜇, we get
(b) d𝓛/d𝜆 = ẋ𝜇 d/d𝜆 (∂𝓛/∂ẋ𝜇) + dẋ𝜇/d𝜆 ∂𝓛/∂ẋ𝜇 = d/d𝜆 (∂𝓛/∂ẋ𝜇 ẋ𝜇). ⇒
(c) d/d𝜆 (𝓛 - ∂𝓛/∂ẋ𝜇 ẋ𝜇) = 0.
This implies, according to (2.2.2),
(d) 𝓗 ≡ 𝓛 - ∂𝓛/∂ẋ𝜇 ẋ𝜇 = 𝑔𝜇𝜈ẋ𝜇ẋ𝜈 = const. ▮
2.3 Christoffel symbols from a Lagrangian
Let us learn a neat trick to compute Christoffel symbol using Lagrangian method. Set the Lagrangian 𝓛 ≡ -𝑔𝜇𝜈ẋ𝜇ẋ𝜈 for the flat FRW metric
(2.3) d𝑠2 = -d𝑡2 + 𝑎(𝑡)𝛿𝑖𝑗d𝑥𝑖d𝑥𝑗.
Applying Euler-Lagrange equation, find an equation for d2𝑥/d𝜆2. Comparing this to the geodesic equation, read 𝛤0𝛼𝛽. Similarly calculate all other Christoffel symbols.
[Solution] The Lagrangian for flat FRW metric is
(a) 𝓛 = ṫ2 - 𝑎2(𝑡)𝛿𝑖𝑗ẋ𝑖ẋ𝑗, where ẋ𝑖 ≡ d𝑥/d𝜆.
Consider the Euler-Lagrange equation for 𝑡:
(b) d/d𝜆 (∂𝓛/∂ṫ) = ∂𝓛/∂𝑡 ⇒ 2ẗ = -2𝑎 d𝑎/d𝑡 𝛿𝑖𝑗ẋ𝑖ẋ𝑗. ⇒
(c) ẗ = -𝑎 d𝑎/d𝑡 𝛿𝑖𝑗ẋ𝑖ẋ𝑗 ≡ -𝛤0𝛼𝛽ẋ𝛼ẋ𝛽.
We can read off
(d) 𝛤000 = 𝛤00𝑖 = 0, 𝛤0𝑖𝑗 = 𝑎 d𝑎/d𝑡 𝛿𝑖𝑗.
Consider the Euler-Lagrange equation for 𝑥𝑘:
(e) d/d𝜆 (∂𝓛/∂ẋ𝑘) = ∂𝓛/∂𝑥𝑘. ⇒ -d/d𝜆 (2𝑎2ẋ𝑘) = 0. ⇒
(f) 𝑎2ẍ𝑘 + 2𝑎 d𝑎/d𝑡 d𝑡/d𝜆 ẋ𝑘 = 0.
So we have
(g) ẍ𝑘 = -2/𝑎 d𝑎/d𝑡 ẋ0ẋ𝑘 ≡ -𝛤𝑘𝛼𝛽ẋ𝛼ẋ𝛽.
We can read off
(h) 𝛤𝑘00 = 𝛤𝑘𝑖𝑗 = 0, 𝛤𝑘0𝑖 = 𝛤𝑘𝑖0 = 1/𝑎 d𝑎/d𝑡 𝛿𝑘𝑖. ▮
2.4 Geodesics in de Sitter space
The line element of de Sitter space (in static patch coordinates) is
(2.4) d𝑠2 = -(1 - 𝑟2/𝑅2) d𝑡2 + (1 - 𝑟2/𝑅2)-1 d𝑟2 + 𝑟2 (d𝜃2 + sin2 𝜃 d𝜙2), where 𝑅2 ≡ 3/𝛬.
Use the Lagrangian method in Problem 2.2 to study the motion of a massive test particle in this spacetime.
1. Derive the conserved energy 𝐸 and angular momentum 𝐿 of the particle.
[Solution] The Lagrangian for the given de Sitter space is
(a) 𝓛 = -𝑔𝜇𝜈 ẋ𝜇ẋ𝜈 = (1 - 𝑟2/𝑅2) ṫ2 - (1 - 𝑟2/𝑅2)-1 𝑟̇2 - 𝑟2 𝜃̇2 - 𝑟2 sin2 𝜃 𝜙̇2, where ẋ ≡ d𝑥/d𝜏.
There is no 𝑡 or 𝜙 in this Lagrangian, so energy 𝐸 and angular momentum 𝐿 are:
(b) 𝐸 ≡ 1/2 ∂𝓛/∂ṫ = (1 - 𝑟2/𝑅2) ṫ, 𝐿 ≡ -1/2 ∂𝓛/∂𝜙̇ = 𝑟2 sin2 𝜃 𝜙̇. ▮
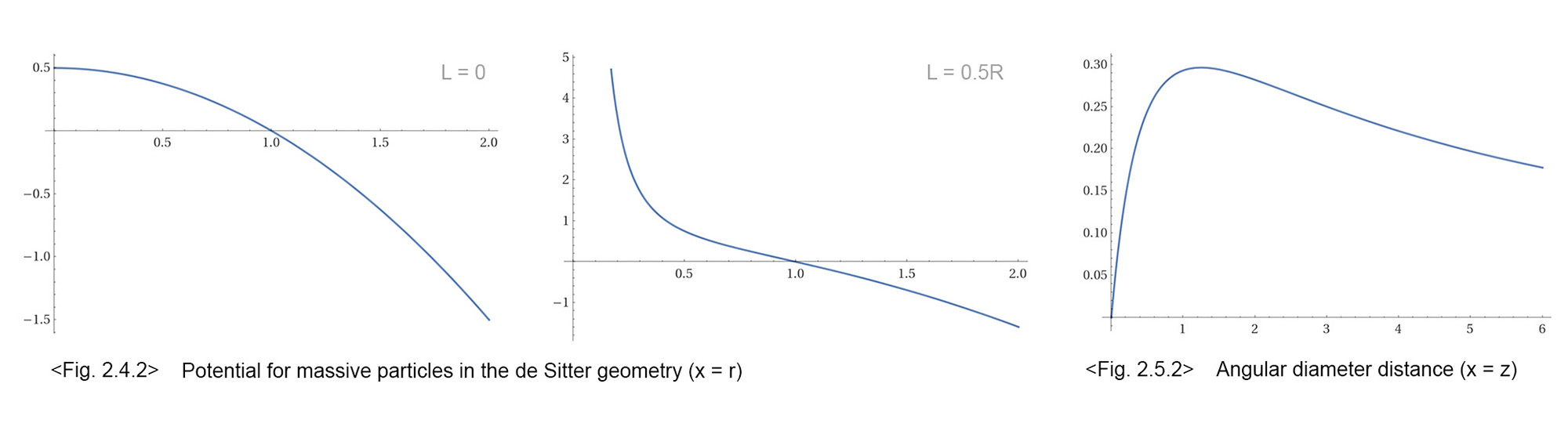
2. Show that the radial motion is described by the potential
(2.4.2) 𝑉(𝑟) = 1 - 𝐿2/𝑅2 + 𝐿2/𝑟2 - 𝑟2/𝑅2.
Sketch this potential for 𝐿 = 0 and 𝐿 = 0.5𝑅.
[Solution] To simply the situation, we can restrict 𝜃 = π/2 and 𝑔𝜇𝜈 ẋ𝜇ẋ𝜈 = -1. then we have
(a) -(1 - 𝑟2/𝑅2) ṫ2 + (1 - 𝑟2/𝑅2)-1 𝑟̇2 + 𝑟2𝜙̇2 = -1,
Using the result of Problem 2.4.1, if we multiply (1 - 𝑟2/𝑅2) at both side and arrange
(b) 𝑟̇2 + (𝑟2𝜙̇2 + 1) (1 - 𝑟2/𝑅2) = (1 - 𝑟2/𝑅2)2 ṫ2 ⇒ 𝑟̇2 + (𝐿2/𝑟2 + 1)(1 - 𝑟2/𝑅2) = 𝐸2.
(c) 1/2 𝑟̇2 + 𝑉(𝑟) = 𝐸total,
where 1/2 𝑟̇2 is kinetic energy and 𝑉(𝑟) is potential energy and total energy 𝐸total = 1/2 𝐸2. Now we can find the potential 𝑉(𝑟):
(d) 𝑉(𝑟) = 1/2 (1 - 𝐿2/𝑅2 + 𝐿2/𝑟2 - 𝑟2/𝑅2).
Hence, if 𝐿 = 0 with 𝑅 ≡ 1, we have equation 𝑉(𝑟) = 1/2 (1 - 𝑟2) and if 𝐿 = 0.5𝑅, we have equation 𝑉(𝑟) = 1/2 (3/4 +1/4𝑟2 - 𝑟2).
In Fig. 2.4.2, this potential is plotted as required (using WolframAlpha). ▮
3. The particle is released with a small radial velocity near 𝑟 = 0. Show that the trajectory is
(2.4.3) 𝑟(𝜏) = 𝑅√(𝐸2 - 1) sinh (𝜏/𝑅),
where 𝜏 is the proper time along the geodesic. We see that the particle reaches the horizon at 𝑟 = 𝑅 in a finite amount of proper time ∆𝜏. Show that the corresponding time ∆𝑡 measured by an observer at 𝑟 = 0 is infinite.
[Solution] Since the direction of the particle is radial, 𝐿 = 0. Using (c) in Solution of Problem 2.4.2,we get
(a) 𝑟̇2 + (1- 𝑟2/𝑅2) = 𝐸2
Then this equation can be, as required, solved by
(b) 𝑟(𝜏) = 𝑅√(𝐸2 - 1) sinh (𝜏/𝑅).
So we see that the particle reaches the horizon at 𝑟 = 𝑅 in a finite amount of proper time ∆𝜏.
Using (b) in Solution of Problem 2.4.1, we get
(c) d𝑡/d𝜏 = 𝐸 (1 - 𝑟2/𝑅2)-1.
We can find that if 𝑟(𝜏) → 𝑅, then 𝑡(𝜏) → ∞. It implies that the corresponding time ∆𝑡 measured by an observer at 𝑟 = 0 is infinite. ▮
2.5 Distances
We will study some unusual properties of the luminosity distance 𝑑𝐿 and the angular diameter distance 𝑑𝛢.
1. Consider the relationship between 𝑑𝐿 and the proper separation 𝓁0 in a flat matter-dominated universe. Show that 𝓁0 = 3𝑡0 [1 - 1/√(1 + 𝑧)] and hence
(2.5.1) 𝑑𝐿 = 𝓁0 (1 - 𝓁0/3𝑡0)-2.
What happens as 𝓁0 → 3𝑡0? How do you interpret this result?
[Solution] According the solution for pure matter universe - the Einstein-de Sitter universe, 𝑎(𝑡) = (𝑡/𝑡0)2/3, considering a redshift 𝑧 from a source the comoving distance to the object is
(a) 𝓁0 = 𝑐 ∫𝑡0𝑡𝑠 = 3𝑡02/3[𝑡01/3 - 𝑡𝑠1/3]𝑐 = 3𝑡0[1 - √𝑎(𝑡𝑠)]𝑐 = 3𝑡0[1 - 1/√(1 + 𝑧)]𝑐.
Using (a) we get
(b) 𝑑𝐿 = 𝓁0(1 + 𝑧) = 𝓁0 (1 - 𝓁0/3𝑡0)-2.
As 𝓁0 → 3𝑡0, 𝑎(𝑡𝑠) → 0 or 𝑧 → ∞, that is the initial Big Bang singularity. This result implies that the current physical size of the universe is thee times its age in light years, assuming a flat matter-dominated universe. ▮
2. Now consider objects of a fixed physical size 𝐷 in a flat matter-dominated universe. Show that the angular diameter of these objects at first decreases with distance, but then becomes larger beyond a critical distance, What is the redshift corresponding to this critical distance? Why does the observed angular size 𝛿𝜃 diverge as 𝑧 → 0 and 𝑧 → ∞?
[Solution] The angular distance of an object at redshift 𝑧 is (RE 2.83)
(a) 𝑑𝛢 = 𝓁0/(1 + 𝑧) ≈ 𝛿𝜃 ∝1/𝐷.
Since in a flat matter-dominated universe 𝐻0 = 2/3𝑡0 (RE 2.151), using (2.5.1a), we get
(b) 𝑑𝛢 = 2/𝐻0 [1/(1 + 𝑧) - 1/(1 + z)3/2].
We can plot it as Fig. 2.5.2 and it shows that 𝑑𝛢 at first grow gradually util 𝑧 = 5/4 and starts to decrease continuously. Since an object of a fixed physical size 𝐷 ∝1/𝑑𝛢, we may say that the angular diameter of these objects at first decreases with distance, but then becomes larger beyond a critical distance. Therefore the redshift corresponding to this critical distance is 𝑧 = 5/4 and the observed angular size 𝛿𝜃 diverge as 𝑧 → 0 and 𝑧 → ∞. ▮
2.8 Einstein's biggist blunder
Einstein introduced the cosmological constant into his field equation to avoid the conclusion that the universe is expanding. In this problem, we will see that this was misguided.
1. Show that for a perfect fluid with positive density and pressure there is no static solution to the Einstein equations.
[Solution] Consider the second Friedmann equation
(a) (𝑑𝑎̇/𝑑𝑡)/𝑎 = -4π𝐺/3 (𝜌 + 3𝑃).
If the universe is filled with a perfect fluid with positive density and pressure, then the right side is nonzero and negative. Hence the universe is decelerating. Because normal matter produce attractive gravity, each elements will attract other element and the universe to decelerate. ▮
2. Consider now a universe with pressureless matter and a cosmological constant. Show that it is possible to obtain a static solution-called the Einstein static universe-if
(2.8.2) 𝛬 = 4π𝐺𝜌𝑚.
What is the spatial curvature of this solution?
[Solution] To obtain a static solution, Einstein introduced an additional fluid, 𝛬, with 𝜌 + 3𝑃 < 0 which creates repulsive gravity, and can balance the attractive force due to the matter. A cosmological constant 𝛬 with 𝑃 = -𝜌 is just such a component. The Friedmann equations with cosmological constant 𝛬 are
(a) (𝑎̇/𝑎)2 = 8π𝐺/3 𝜌𝑚 + 𝛬/3 - 𝑘/(𝑎2𝑅02).
(b) (𝑑𝑎̇/𝑑𝑡)/𝑎 = -4π𝐺/3 𝜌𝑚 + 𝛬/3.
So we need that 𝑑𝑎̇/𝑑𝑡 = 0, which makes, as required,
(c) 𝛬 = 4π𝐺𝜌𝑚.
This implies that we can find a solution with 𝑑𝑎̇/𝑑𝑡 = 0. Additionally, we need that 𝑎̇ = 0 as well. If we use (c), (a) becomes
(d) (𝑎̇/𝑎)2 = 𝛬 - 𝑘/(𝑎2𝑅02).
Hence, the static universe needs to be that the curvature is positive and 𝛬 ∝ 𝑅0-2. ▮
3. Show that the Einstein static universe is unstable to small perturbations.
Hint: Consider a small perturbation around the static solution
(2.8.3.1) 𝜌𝑚(𝑡) = 𝜌𝑚,0[1 + 𝛿(𝑡)],
(2.8.3.2) 𝑎(𝑡) = 1 + 𝜖(𝑡),
with ∣𝛿∣ ≪ 1 and ∣𝜖∣ ≪ 1. Show that the perturbations 𝛿 and 𝜖 are related to each other and that they grow exponentially with time.
[Solution] The matter density satisfies 𝜌𝑚(𝑡) = 𝜌𝑚,0𝑎-3, so we get,
(a) 𝛿 = 𝑎-3 -1 = (1 + 𝜖)-3 - 1 ≈ -3𝜖,
where we apply Taylor series expansion and leave the first order one. Using 𝛬 = 4π𝐺𝜌𝑚, (b) in (2.8.2) becomes
(b) 𝑑𝜖̇/𝑑𝑡 = -4π𝐺/3 𝜌𝑚,0(1 - 3𝜖) + 𝛬/3 = -𝛬/3(1 - 3𝜖) + 𝛬/3 = 𝛬𝜖.
We can find the solution as
(c) 𝜖(𝑡) = 𝑐1𝑒√𝛬 𝑡 + 𝑐2𝑒-√𝛬 𝑡.
This implies that depending on the sign of the initial perturbation, the perturbations will grow or collapse exponentially with time. ▮
2.9 The accelerating universe
Consider a universe with spatial curvature, pressureless matter and a positive cosmological constant.
1. The deceleration parameter is defined as
(2.9.1a) 𝑞(𝑡) ≡ - (𝑑𝑎̇/𝑑𝑡)𝑎/𝑎̇2.
Plot 𝑞(𝑡) as a function of 𝑎(𝑡) for our universe, with 𝛺𝑚 = 0.3 and 𝛺𝛬 = 0.7. Show that today
(2.9.1b) 𝑞0 = 𝛺𝑚/2 - 𝛺𝛬.
What is the value for our universe?
[Solution] Recall the second Friedmann equation and using 𝜔𝑖 = 𝑃𝑖/𝑐2
(a) (𝑑𝑎̇/𝑑𝑡)/𝑎 = -4π𝐺/3 𝛴𝑖(𝜌𝑖 + 3𝑃𝑖/𝑐2) = -4π𝐺/3 𝛴𝑖(𝜌𝑖 + 3𝜔𝑖)
Using 𝜌𝑐 = 3𝐻2/8π𝐺, 𝛺𝑖 ≡ 𝜌𝑖/𝜌𝑐, the value of 𝜔𝑖 is 0 for matter, 1/3 for radiation and -1 for cosmological constant or dark energy (𝛬), we get
(b) 𝑞 = 1/2 𝛴 𝛺𝑖(1 + 3𝜔𝑖) = 𝛺𝑟 + 1/2 𝛺𝑚 - 𝛺𝛬.
Since at present 𝛺𝑚 = 0.3 and 𝛺𝛬 = 0.7 we find
(c) 𝑞0 = 𝛺𝑚/2 - 𝛺𝛬 = -0.55. ▮
2. The jerk is defined as
(2.9.2a) 𝐽(𝑡) ≡ (𝑑2𝑎̇/𝑑𝑡2)𝑎2/𝑎̇3.
Show that
(2.9.2b) 𝐽(𝑡) = 1 + 1/𝑎2𝐻2 𝑘𝑐2/𝑅02,
so that the jerk is one for a flat universe.
[Solution] The second Friedmann equations without radiation
(a) (𝑑𝑎̇/𝑑𝑡)/𝑎 = -𝐻02/2 [𝛺𝑚𝑎-3 - 2𝛺𝛬] ⇒ 𝑑𝑎̇/𝑑𝑡 = 𝐻02(-1/2 𝛺𝑚𝑎-2 + 𝛺𝛬𝑎).
Taking a time derivative on both sides, we get
(b) 𝑑2𝑎̇/𝑑𝑡2 = 𝐻02(𝛺𝑚𝑎-3 + 𝛺𝛬)𝑎̇. ⇒
(c) 𝐽(𝑡) = (𝑑2𝑎̇/𝑑𝑡2)𝑎2/𝑎̇3 = (𝑑2𝑎̇/𝑑𝑡2)𝑎2/𝑎̇𝐻2 = [𝐻02(𝛺𝑚𝑎-3 + 𝛺𝛬)]/𝐻2.
Since we can write Friedmann equation without radiation as 𝐻2 = 𝐻02(𝛺𝑚𝑎-3 + 𝛺𝛬) - 𝑘𝑐2/𝑎2𝑅02, we find
(d) 𝐽(𝑡) = 1/𝐻2 [𝐻02(𝛺𝑚𝑎-3 + 𝛺𝛬) - 𝑘𝑐2/𝑎2𝑅02 + 𝑘𝑐2/𝑎2𝑅02] = 1 + 1/𝑎2𝐻2 𝑘𝑐2/𝑅02.
Hence, the jerk is one for 𝑘 = 0, a flat universe. ▮
Now specialize to the case of a flat universe.
3. Find the redshift at which the energy density of the universe becomes dominated by the cosmological constant. What is the value for our universe?
[Solution] When the energy density of matter is equal to that of the cosmological constant, we find
(a) 𝛺𝑚𝑎𝛬-3 = 𝛺𝛬.
(b) 𝑎𝛬-1 = 1 + 𝑧𝛬 = (𝛺𝛬/𝛺𝑚)1/3 = [(1 - 𝛺𝑚)/𝛺𝑚]1/3. ⇒ 𝑧𝛬 = (1/𝛺𝑚 - 1)1/3 -1.
For our universe, according to Wikipedia 'Chronology of the universe', it happened about 9.8 Ga, so we can calculate
(c) 𝑎𝛬 = 9.8/13.9 = 1/(1 + 𝑧𝛬). ⇒ 𝑧𝛬 ≈ 0.4.
4. Find the redshift at which the universe begins accelerating.
[Solution] 𝑑2𝑎̇/𝑑𝑡2 > 0 means the accelerating of expansion, using (a) in (2.9.2) we find
(a) 𝛺𝑚𝑎acc-3 - 2𝛺𝛬 = 0. ⇒
(b) 𝑎acc-1 = 1 + 𝑧acc = (2𝛺𝛬/𝛺𝑚)1/3 = 21/3 (1 + 𝑧𝛬). ⇒ 𝑧acc = 21/3 (1 + 𝑧𝛬) -1 ≈ 0.76. ▮
5. Show that the solution for scale factor is of the form
(2.9.5) 𝑎(𝑡) = 𝛢(sinh 𝛼𝑡)2/3,
where 𝛢 and 𝛼 should be expressed in terms of 𝛺𝑚 and 𝐻0.
• Verify that your solution has the correct limits at early and late times.
[Solution] Consider Friedmann equation in terms of energy density with 𝛺𝑚 + 𝛺𝛬 = 1:
(a) (𝑎̇/𝑎)2 = 𝐻2 = 𝐻02 [𝛺𝑚/𝑎3 + 𝛺𝛬] ⇒ 𝑎̇2 = 𝐻02 [𝛺𝑚/𝑎 + 𝛺𝛬𝑎2].
We define 𝑥2 = 𝑎3 and 𝑦 ≡ √(𝛺𝛬/𝛺𝑚) 𝑥 then we have
(b) 𝑥̇2 = (3/2 𝐻0)2𝛺𝑚 [1 + 𝛺𝛬/𝛺𝑚 𝑥2. ⇒ 𝑦̇2 = (3/2 𝐻0)2𝛺𝛬 (1 + 𝑦2). ⇒ (3/2 𝐻0)2𝛺𝛬 = (d𝑦/d𝑡)/√(1 + 𝑦2).
(c) 3/2 √𝛺𝛬𝐻0 d𝑡 = d𝑦/√(1 + 𝑦2). ⇒ 3/2 √𝛺𝛬𝐻0𝑡 = ∫ d𝑦/√(1 + 𝑦2) = sinh-1 𝑦,
where we dropped constant because 𝑦 = 0 at 𝑡 = 0.
(d) 𝑦 ≡ √(𝛺𝛬/𝛺𝑚) 𝑥 = √(𝛺𝛬/𝛺𝑚) 𝑎(𝑡)3/2 = sinh (3/2 √𝛺𝛬𝐻0𝑡). ⇒ 𝑎(𝑡) = (𝛺𝛬/𝛺𝑚)1/3 [sinh (3/2 √𝛺𝛬𝐻0𝑡)]2/3.
Hence 𝛢 = (𝛺𝛬/𝛺𝑚)1/3 and 𝛼 = 3/2 √𝛺𝛬𝐻0.
• At early times, 𝐻0𝑡 ≪ 1, so we get 𝑎(𝑡) ∝ 𝑡2/3 by Taylor series expansion and since sinh 𝛼𝑡 = 1/2 (𝑒𝛼𝑡/2 - 𝑒-𝛼𝑡), at late times, 𝐻0𝑡 ≫ 1, so we have the exponential growth.
6. Compare the luminosity distance as a function of the redshift. Plot for 𝛺𝑚 = 1.0 and 𝛺𝑚 = 0.3; compare the result to Fig. 2.6. Consider supernova measurements with a minimum redshift of 0.5. How accurate do the measurements of 𝑑𝐿 have to be in order to distinguish the two models?
[Solution] The luminosity distance in a flat universe is [RE (2.67)]
(a) 𝑑𝐿(𝑧; 𝛺𝑚) = (1 + 𝑧) 𝑑𝑀(𝑧) = (1 + 𝑧) 𝑐 ∫𝑧0 d𝑧/𝐻(𝑧) = (1 + 𝑧) 𝑐/𝐻0 ∫𝑧0 d𝑧'/√[𝛺𝑚(1 + 𝑧')3 + (1- 𝛺𝑚)].
This gives Fig. 2.6 which plots Luminosity distance in units of 𝑐/𝐻0 as a function of redshift 𝑧. For 𝑧 = 0.5 with 𝐻0 = 68 km s-1 Mpc-1, we get
(b) 𝑑𝐿(𝑧 = 0.5; 𝛺𝑚 = 1.0) = 2.43 Gpc.
(c) 𝑑𝐿(𝑧 = 0.5; 𝛺𝑚 = 0.3) = 2.93 Gpc.
then the ratio of the two values is
(d) 𝑑𝐿(𝑧 = 0.5; 𝛺𝑚 = 0.3)/𝑑𝐿(𝑧 = 0.5; 𝛺𝑚 = 1.0) ≈ 1.2.
So the measurements of 𝑑𝐿 of the two models are distinguished by 20% accuracy. ▮
2.10 Phantom dark energy
Dark energy is most likely a cosmological constant with equation of state 𝜔 = -1. Radical alternatives have nevertheless been considered. In this problem we will study the dynamics of "phantom dark energy" with 𝜔 < -1.
1. Consider a flat universe with matter (𝑚) and phantom dark energy (𝑋). Show that the energy density of the dark energy increases with time. If the scale factor today is 𝑎0 ≡ 1, show that in the future
(2.10.1) 𝛺𝑋(𝑎) ≡ 𝜌𝑋(𝑎)/𝜌crit(𝑎) = (1 + 𝛺𝑚,0/𝛺𝑋,0 𝑎3𝜔𝑋)-1.
If 𝛺𝑋,0 = 0.75 and 𝜔𝑋 = -2, at what scale factor is 99.9% of the energy density in dark energy?
[Solution] The evolution of the energy density depends on the continuity equation and equation of state 𝜔 = 𝑃/𝜌𝑐2
(a) 𝜌̇ + 3 𝑎̇/𝑎 (𝜌 + 𝑃/𝑐2) = 0, (d ln 𝜌)/(d ln 𝑎) = -3(1 + 𝜔), ⇒ 𝜌 ∝ 𝑎-3(1 + 𝜔).
So the dark energy also increases with time.
(b) 𝛺𝑋(𝑎) ≡ 𝜌𝑋(𝑎)/𝜌crit(𝑎) = 𝜌𝑋(𝑎)/[𝜌𝑚(𝑎) + 𝜌𝑋(𝑎)] = 𝛺𝑋,0𝑎-3(1+3𝜔𝑋)/[𝛺𝑚,0𝑎-3 + 𝛺𝑋,0𝑎-3(1+3𝜔𝑋)] = (1 + 𝛺𝑚,0/𝛺𝑋,0 𝑎3𝜔𝑋)-1.
Hence, for 𝛺𝑋,0 = 0.75 and 𝜔𝑋 =-2, if we have 99.9% of the energy density, the scale factor 𝑎99.9:
(c) 0.999 = (1 + 0.25/0.75 𝑎99.9-6) ⇒ 𝑎99.9 ≈ 2.6. ▮
2. If the dark energy density dominates the matter density at a time 𝑡*, show that 𝑎 → ∞ in a finite time ∆𝑡. This divergence of the scale factor has been called a "Big Rip." Find ∆𝑡 in terms of 𝜔𝑋 and Hubble parameter 𝐻* at the time 𝑡*.
[Solution] When the dark energy density dominates the matter density, we have
(a) (𝑑𝑎/𝑑𝑡)/𝑎 = 𝐻 = 𝐻* (𝑎/𝑎*)-3(1+𝜔𝑋)/2.
Integrating both sides, we get
(b) ∆𝑡 = ∫𝑡*+∆𝑡𝑡* d𝑡 = 1/𝐻* 𝑎*-3(1+𝜔𝑋)/2 ∫𝑎'𝑎* 𝑎3(1+𝜔𝑋)/2 d ln 𝑎.
This integral converges for 𝑎' → ∞ with 𝜔𝑋 < 1 and gives
(c) ∆𝑡 = 1/𝐻* 𝑎*-3(1+𝜔𝑋)/2 [2/3(1 + 𝜔𝑋) 𝑎3(1 + 𝜔𝑋)/2]∞𝑎* = 2/3𝐻*∣1 + 𝜔𝑋∣.
3. What would happen to the observed wavelength of CMB photons as the Big Rip is approach?
[Solution] As the Big Rip is approach, 𝑎 → ∞, CM photons become increasingly redshifted and ultimately we cannot observe them. ▮
|
|
|





































