|
김관석
|
2024-10-24 16:52:28, 조회수 : 97 |
- Download #1 : BC_6b.jpg (80.7 KB), Download : 0

6.1.3 Conservation Equations
Our next task is to derive the evaluation for the perturbations The evolution of the metric is governed by the Einstein equation 𝐺𝜇𝜈 = 8π𝐺 𝛵𝜇𝜈, while the evolution of the matter perturbations follows from the conservation of the energy-momentum tensor, ∇𝜇𝛵𝜇𝜈 = 0. Expanding these equations to linear order in the perturbations will gives us the linearized equations of the motion for the matter and metric perturbations.
It will be convenient to use the Newtonian gauge where metric is
(6.62) 𝑔𝜇𝜈 = diag[-𝑎2(1 + 2𝛹), 𝑎2(1 - 2𝛷)𝛿̇𝑖𝑗].
We will derive the equation of motion for the matter perturbations by linearizing ∇𝜇𝛵𝜇𝜈 = 0. Note that if there is no energy and momentum tranasfer between the different components, then the species are separately conserved and we have ∇𝜇𝛵𝑎𝜇𝜈 = 0 with all species separately. So we have
(6.63) ∇𝜇𝛵𝜇𝜈 = 0 = ∂𝜇𝛵𝜇𝜈 + 𝛤𝜇𝜇𝛼𝛵𝛼𝜈 - 𝛤𝛼𝜇𝜈𝛵𝜇𝛼.
To evaluate this, we need the purturbated connection coefficients. Using the metric metric (6.62), it is a straightforward exercise to shoe that
(6.64-66) 𝛤000 = 𝓗 + 𝛹ʹ, 𝛤0𝑖0 = ∂𝑖𝛹, 𝛤𝑖00 = ∂𝑖𝛹,
(6.67-69) 𝛤0𝑖𝑗 = 𝓗𝛿̇𝑖𝑗 - [𝛷ʹ + 2𝓗(𝛷 + 𝛹)]𝛿̇𝑖𝑗, 𝛤𝑖𝑗0 = (𝓗 - 𝛷ʹ)𝛿̇𝑖𝑗, 𝛤𝑖𝑗𝑘 = 2𝛿̇𝑖(𝑗∂𝑘)𝛷 + 𝛿̇𝑗𝑘∂𝑖𝛷.
Example Recall the general expression expression for the connection coefficients
(6.70) 𝛤𝛼𝛽𝛾 = 1/2 𝑔𝛼𝜌(∂𝛽𝑔𝜌𝛾 + ∂𝛾𝑔𝛽𝜌 - ∂𝜌𝑔𝛽𝛾).
To evaluate this, we need the inverse of the metric (6.62)
(6.71) 𝑔𝜇𝜈 = diag[-𝑎-2(1 - 2𝛷), 𝑎-2(1 + 2𝛹)𝛿̇𝑖𝑗].
where we have used that to linear order (1 + 2𝛹)-1 ≈ (1 - 2𝛹). Applying this to 𝛤000, we then have
(6.72) 𝛤000 = 1/2 𝑔0𝜌(∂0𝑔𝜌0 + ∂0𝑔0𝜌 - ∂𝜌𝑔00) = 1/2 𝑔00(∂0𝑔00 + ∂0𝑔00 - ∂𝜌𝑔00) = 1/2 𝑔00∂0𝑔00
= 1/2 𝑎-2(1 - 2𝛹)∂0[𝑎2(1 + 2𝛹)] = 𝑎-2[𝑎𝑎ʹ(1 + 2𝛹) + 𝑎2𝛹ʹ] ≈ 𝓗 + 𝛹ʹ. ▮
Exercise 6.6 Derive (6.65)-(6.69).
Substituting the perturbed connection efficient into (6.63), we can derive the linearized evolution equations for the matter perturbations. The algebra is a bit involved and the results are summarized below.
• Continuity equation Setting 𝜈 = 0 in (6.63), we find
(6.73) 𝛿𝜌̄ʹ = -3𝓗(𝛿𝜌 + 𝛿𝑃) - ∂𝑖𝑞𝑖 + 3𝛷ʹ(𝜌̄ + 𝑃̄),
which describe the evolution of the density perturbation. On the right-hand side the first term is the dilution due to the background expansion, the second term accounts for the local fluid flow, and the last term is a purely relativistic effect corresponding to the density changes caused by perturbations to the local expansion rate. This arises because we can think of (1 - 𝛷)𝑎 is the "local scale factor" in the spatial part of the metric in Newtonian gauge. The first and last terms are therefore related. Substituting 𝛿𝜌 = 𝜌̄𝛿 and 𝑞𝑖 = (𝜌̄ + 𝑃̄)𝑣𝑖 into (6.73), we get evolution equation for the density contrast
(6.74) 𝛿ʹ = -(1 + 𝑃̄/𝜌̄)(𝛁 ⋅ 𝐯 - 3𝛷ʹ) - 3𝓗(𝛿𝑃/𝛿𝜌 - 𝑃̄/𝜌̄)𝛿 .
In the limit of 𝑃 ≪ 𝜌, we recover the Newtonian equation (5.138), written conformal time, 𝛿ʹ = -𝛁 ⋅ 𝐯 + 3𝛷ʹ, but with a relativistic correction coming from the perturbed expansion rate. This correction is small on sub-Hubble scales and we reproduce the Newtonian limit.
• Euler equation Setting 𝜈 = 𝑖 in (6.63), we get
(6.75) 𝑞𝑖ʹ = -4𝓗𝑞𝑖 - (𝜌̄ + 𝑃̄)∂𝑖𝛿𝑃 - ∂𝑗𝜫𝑖𝑗,
which is the relativistic version of the Euler equation.The first term on the right-hand side enforces the expected scaling of the momentum density, 𝑞 ∝ 𝑎-4. The remaining terms are force terms due to gravity, pressure and anisotropic stress. substituting 𝑞𝑖 = (𝜌̄ + 𝑃̄)𝑣𝑖 into (6.75), we get an evolution of bulk velocity
(6.76) 𝑣𝑖ʹ = -[𝓗 + 𝑃̄ʹ/(𝜌̄ + 𝑃̄)]𝑣𝑖 - 1/(𝜌̄ + 𝑃̄) (∂𝑖𝛿𝑃 + ∂𝑗𝛱𝑖𝑗) - ∂𝑖𝛹,
which should be compared to the Newtonian equation (5.139).
Derivation Consider first the 𝜈 = 0 component of (6.63) [RE (6.33)]
(6.77) ∂0𝛵00 + ∂𝑖𝛵𝑖0 + 𝑂(2)𝛤𝜇𝜇𝑖𝛵𝑖0 - 𝛤000𝛵00 - 𝑂(2)𝛤0𝑖0𝛵𝑖0 - 𝑂(2)𝛤𝑖00𝛵0𝑖 - 𝛤𝑖𝑗0𝛵𝑗𝑖 = 0.
Substituting the perturbed connection coefficients gives
(6.78) -(𝜌̄ + 𝛿𝜌)ʹ - ∂𝑖𝑞𝑖 - (𝓗 + 𝛹ʹ + 3𝓗 - 3𝛷ʹ)(𝜌̄ + 𝛿𝜌) + (𝓗 + 𝛹ʹ)(𝜌̄ + 𝛿𝜌) - (𝓗 - 𝛷ʹ)𝛿𝑖𝑗(𝑃̄ + 𝛿𝑃)𝛿𝑗𝑖 = 0, and hence
(6.79) 𝜌̄ʹ + 𝛿𝜌ʹ + ∂𝑖𝑞𝑖 + 3𝓗(𝜌̄ + 𝛿𝜌) - 3𝜌̄𝛷ʹ + 3𝓗(𝑃̄ + 𝛿𝑃) - 3𝑃̄𝛷ʹ = 0.
Writing the zeroth-order and first-order parts separately, we get
(6.80-1) 𝜌̄ʹ = -3𝓗(𝜌̄ + 𝑃̄). 𝛿𝜌ʹ = -3𝓗(𝛿𝜌 + 𝛿𝑃) - ∂𝑖𝑞𝑖 + 3𝜌𝛷ʹ(𝛿𝜌 + 𝛿𝑃).
(6.80) is simply the conservation of energy in the homogeneous background. (6.81) is the continuity equation for the density perturbation 𝛿𝜌. next consider 𝜈 = 𝑖 component of (6.63)
(6.82) ∂0𝛵0𝑖 + ∂𝑗𝛵𝑗𝑖 + 𝛤𝜇𝜇0𝛵0𝑖 + 𝛤𝜇𝜇𝑗𝛵𝑗𝑖 - 𝛤00𝑖𝛵00 - 𝛤0𝑗𝑖𝛵𝑗0 - 𝛤𝑖0𝑖𝛵0𝑗 - 𝛤𝑗𝑘𝑖𝛵𝑘𝑗 = 0.
Substituting the perturbed energy-momentum tensor, with 𝛵0𝑖 = +𝑞𝑖 and 𝛵𝑖0 = -𝑞𝑖, and the perturbed connection coefficients gives
(6.83) 𝑞𝑖ʹ + ∂𝑗[(𝑃̄ + 𝛿𝑃)𝛿𝑗𝑖 + 𝛱𝑗𝑖] + 4𝓗𝑞𝑖 + (∂𝑗𝛹 - 3∂𝑗𝛷)𝑃̄𝛿𝑗𝑖 + ∂𝑖𝛹𝜌̄ + 𝓗𝛿𝑗𝑖𝑞𝑖 - 𝓗𝛿𝑗𝑖𝑞𝑗 - (-2𝛿𝑗(𝑘∂𝑖)𝛷 + 𝛿𝑘𝑖∂𝑗𝛷)𝑃̄𝛿𝑗(𝑘 = 0. Cleaning this up, we find
(6.84) 𝑞𝑖ʹ = -4𝓗𝑞𝑖 - (𝜌̄ + 𝑃̄)∂𝑖𝛹 - ∂𝑖𝛿𝑃 - ∂𝑗𝛱𝑖𝑗. ▮
• Matter Consider a non-relativistic fluid (i.e. matter), with 𝑃𝑚 = 0 and 𝛱𝑖𝑗𝑚.
The continuity and Euler equations then simplify considerably
(6.85-6) 𝛿ʹ𝑚 = -𝛁 ⋅ 𝐯𝑚 + 3𝛷ʹ, 𝐯ʹ𝑚 = -𝓗𝐯𝑚 - 𝛁𝛹.
Combining the time derivative of (6.85) with the divergence of (6.86), we find [verification needed]
(6.87) 𝛿ʺ𝑚 + 𝓗𝛿ʹ𝑚 ← friction = ∇2𝛹 ← gravity + 3(𝛷ʺ + 𝓗𝛷ʹ).
Except for the terms arising from the time dependence of potential, this is the same as the Newtonian equation for the matter perturbations. We will apply this to the clustering of dark matter perturbation.
• Radiation For a relativistic perfect fluid (i.e. radiation with no viscosity), we have 𝑃𝑟 = 1/3 𝜌𝑟 and 𝛱𝑖𝑗𝑟 = 0. The continuity and Euler equations then become
(6.88-9) 𝛿ʹ𝑟 = -4/3 𝛁 ⋅ 𝐯𝑟 + 4𝛷ʹ, 𝐯ʹ𝑟 = -1/4 𝛁𝛿𝑟 - 𝛁𝛹.
Combining the time derivative of (6.88) with the divergence of (6.89), we get
(6.90) 𝛿ʺ𝑟 - 1/3 ∇2𝛿𝑟 = 4/3 ∇2𝛹 + 4𝛷ʺ,
where ∇2𝛿𝑟 is about pressure and ∇2𝛹 is about gravity. We see that radiation perturbations don't experience the Hubble friction, but fee an additional pressure-induced force. Below how this equation allows for sound waves in the primordial plasma will be shown.
Sound waves and Summary
For future reference we collect here the linearized continuity and Euler equations:
(6.91) 𝛿ʹ = -(1 + 𝑃̄/𝜌̄)(∂𝑖𝑣𝑖 - 3𝛷ʹ) - 3𝓗(𝛿𝑃/𝛿𝜌 - 𝑃̄/𝜌̄)𝛿,
(6.92) 𝑣𝑖ʹ = -[𝓗 + 𝑃̄ʹ/(𝜌̄ + 𝑃̄)]𝑣𝑖 - 1/(𝜌̄ + 𝑃̄) (∂𝑖𝛿𝑃 + ∂𝑗𝛱𝑖𝑗) - ∂𝑖𝛹.
We typically work with these equations in Fourier space. For scalar fluctuations, we obtain the equations for the individual Fourier modes by the following replacement:
(6.93) ∂𝑖 → 𝑖𝑘𝑖, 𝑣𝑖 → 𝑖𝑘̂𝑖𝑣, 𝛱𝑖𝑗 → -(𝜌̄ + 𝑃̄)𝑘̂⟨𝑖𝑘̂𝑗⟩𝛱,
where 𝑘̂⟨𝑖𝑘̂𝑗⟩ ≡ 𝑘̂𝑖𝑘̂𝑗 - 1/3 𝛿𝑖𝑗. Note that we have absorbed factors of 𝑘 ≡ ∣𝐤∣ in 𝑣 and 𝛱-as well as rescaled the anisotropic stress by a factor of (𝜌̄ + 𝑃̄)-so that 𝑣(𝜂, 𝐤) and 𝛱(𝜂, 𝐤) are not quite the Fourier transforms of 𝑣(𝜂, 𝐱) and 𝛱(𝜂, 𝐱). Equations (6.91) and (6.92) then lead to
(6.94) 𝛿ʹ = -(1 + 𝑃̄/𝜌̄)(𝑘𝑣𝑖 - 3𝛷ʹ) - 3𝓗(𝛿𝑃/𝛿𝜌 - 𝑃̄/𝜌̄)𝛿,
(6.95) 𝑣𝑖ʹ = -[𝓗 + 𝑃̄ʹ/(𝜌̄ + 𝑃̄)]𝑣 - 1/(𝜌̄ + 𝑃̄) 𝑘𝛿𝑃 + 2/3 𝑘𝛱 - 𝑘𝛹.
These equations apply separately for all components that aren't directly coupled to each other. For example, dark matter doesn't interact with other matter (except through gravity), so it satisfies its own conservation equations. In general, we will have separation equations for each species with perturbation (𝛿𝑎, 𝑣𝑎, 𝛿𝑃𝑎, 𝛱𝑎). The gravitational coupling between the different species is captured by the expansion rate 𝓗 and the metric potentials 𝛷 and 𝛹. We must make further simplifying assumptions and additional equations to describe evolution of the four perturbations (𝛿, 𝑣, 𝛿𝑃, 𝛱).
• Sometime we will assume a perfect fluid. Such a fluid is characterized by strong interactions which keep the pressure isotropic, 𝛱 = 0. For a barotropic fluid, with 𝑃 = 𝑃(𝜌), we can write as 𝛿𝑃 = 𝑐𝑠2, where the sound speed is
(6.96) 𝑐𝑠2 ≡ 𝑑𝑃/𝑑𝜌 = 𝑃̄ʹ/𝜌̄ʹ.
For general fluid, the pressure may not just depend on density and the sound speed defined as
(6.97) 𝑐𝑠2 ≡ (∂𝑃/∂𝜌)𝑆 = 𝑃̄ʹ/𝜌̄ʹ,
where the subscript indicate that the derivative is taken at fixed entropy and the second equality assumes that the expansion of the back ground is adiabatic (i.e. there is no entropy production). The perturbations are called adiabatic if
(6.98) 𝛿𝑃 = 𝑐𝑠2𝛿𝜌 = 𝑃̄ʹ/𝜌̄ʹ 𝛿𝜌.
Note that the perturbations in a barotropic fluid are necessarily adiabatic, but this is not the case. If the perturbations are adiabatic, then they are described by only independent variables, 𝛿 and 𝑣 in the continuity and Euler equations.
• Decoupled or weakly interacting species (e.g. neutrinos) cannot be described by the above method, so we have to solve the Boltzmann equation for the evolution of the perturbed distribution function 𝑓 (see Appendix B).
• Decoupled dark matter is collisionless and has a negligible velocity dispersion. It behave like a pressureless perfect fluid although it has no interactions and therefore is not the traditional one [6].
6.1.4 Einstein Equations
Wee see from (91) and (6.92) that the evolution of each matter species is influenced by the metric potential 𝛷 and 𝛹. To close the system of equations, we need equations for the evolution of the metric perturbations. These follows from the Einstein equation. Deriving the linearized Einstein equation in Newtonian gauge is conceptually straightforward, but a bit tedious. So we do the computation once by hand and we had better use Mathematica or alternative to perform algebra.
We require the perturbation to the Einstein tensor, 𝐺𝜇𝜈 ≡ 𝑅𝜇𝜈 - 1/2 𝑅𝑔𝜇𝜈, so we first need to calculate the perturbed Ricci tensor 𝑅𝜇𝜈 and Ricci scalar 𝑅.
• Ricci tensor Recall that the Ricci tensor can be expressed in terms of the connection coefficients as [RE (2.120)]
(6.99) 𝑅𝜇𝜈 = ∂𝜆𝛤𝜆𝜇𝜈 - ∂𝜈𝛤𝜆𝜇𝜆 + 𝛤𝜆𝜆𝜌𝛤𝜌𝜇𝜈 - 𝛤𝜌𝜇𝜆𝛤𝜆𝜈𝜌.
Substituting the perturbed connection coefficient (6.64)-(6.69),
(6.100) 𝑅00 = -3𝓗ʹ + ∇2𝛹 + 3𝓗(𝛷ʹ + 𝛹ʹ) + 3𝛷ʺ,
(6.101) 𝑅0𝑖 = 2∂𝑖(𝛷ʹ + 𝓗𝛹),
(6.102) 𝑅𝑖𝑗 = [𝓗ʹ + 2𝓗2 - 𝛷ʺ + ∇2𝛷 -2(𝓗ʹ + 2𝓗2)(𝛷 + 𝛹) - 𝓗𝛹' -5𝓗𝛷ʹ]𝛿𝑖𝑗 + ∂𝑖∂𝑗(𝛷 - 𝛹).
Example The temporal component of Ricci tensor is
(6.103) 𝑅00 = ∂𝜌𝛤𝜌00 - ∂0𝛤𝜌0𝜌 + 𝛤𝛼00𝛤𝜌𝛼𝜌 - 𝛤𝛼0𝜌𝛤𝜌0𝛼.
When 𝜌 = 0, 𝑅00 = 0, so we get
(6.104) 𝑅00 = ∂𝑖𝛤𝑖00 - ∂0𝛤𝑖0𝑖 + 𝛤𝑖𝑖𝜌𝛤𝜌00 - 𝛤𝜌0𝑖𝛤𝑖0𝜌 = ∂𝑖𝛤𝑖00 - ∂0𝛤𝑖0𝑖 + 𝛤𝑖𝑖0𝛤000 + 𝑂(2)𝛤𝑖𝑖𝑗𝛤𝑗00 - 𝑂(2)𝛤00𝑖𝛤𝑖00 -𝛤𝑗0𝑖𝛤𝑖0𝑗.
= ∇2𝛹 - 3∂0(𝓗 - 𝛷ʹ) + 3(𝓗 + 𝛹ʹ)(𝓗 - 𝛷ʹ) - (𝓗 - 𝛷ʹ)2𝛿𝑗𝑖𝛿𝑖𝑗 = -3𝓗ʹ + ∇2𝛹 + 3𝓗(𝛷ʹ + 𝛹ʹ) + 3𝛷ʺ. ▮
Exercise 6.7 Derive (6.101) and (6.102). Verify the results using the Mathematica notebook provide on the book's website.
• Ricci scalar We can compute according to 𝑅 = 𝑅𝜇𝜇 = 𝑔𝜇𝜈𝑅𝜇𝜈
(6.105) 𝑅 = 𝑔00𝑅00 + 𝑂(2)2𝑔0𝑖𝑅0𝑖 + 𝑔𝑖𝑗𝑅𝑖𝑗.
Since, according to (6.71), 𝑔𝑖𝑗 = diag[-𝑎-2(1 - 2𝛹), 𝑎-2(1 + 2𝛷)𝛿𝑖𝑗]
(6.106) 𝑎2𝑅 = -(1 - 2𝛹)𝑅00 + (1 + 2𝛷)𝛿𝑖𝑗𝑅𝑖𝑗 = (1 - 2𝛹)[3𝓗ʹ - ∇2𝛹 - 3𝓗(𝛷ʹ + 𝛹ʹ) - 3𝛷ʺ] + 3(1 + 2𝛷)[𝓗ʹ + 2𝓗∇2 - 𝛷ʺ + ∇2𝛷 - 2(𝓗ʹ + 2𝓗2)(𝛷 + 𝛹) - 𝓗𝛹ʹ - 5𝓗𝛷ʹ] + (1 + 2𝛷)∇2(𝛷 - 𝛹), dropping nonlinear terms
𝑎2𝑅 = 6(𝓗ʹ + 𝓗2) - 2∇2𝛷 -12(𝓗ʹ + 𝓗2)𝛹 - 6𝛷ʺ - 6𝓗(𝛹ʹ + 3𝛷ʹ),
where the first term is the homogeneous part discussed in Chapter 2 and the other part is the linear correction.
• Einstein equation We are ready to compute the Einstein equation
(6.107) 𝐺𝜇𝜈 = 8π𝐺𝛵𝜇𝜈.
We chose to work with one index raised since it simplify the form of the energy-momentum tensor. When 𝜇 = 𝜈 = 0,
(6.109) 𝐺00 = 𝑔0𝜇𝐺𝜇0 = 𝑔00[𝑅00 - 1/2 𝑔00𝑅 = -𝑎-2(1 - 2𝛹)𝑅00 - 1/2 𝑅,
where we used that 𝑔0𝑖 = 0 in Newtonian gauge. Substituting (6.100) and (6.107),
(6.110) 𝛿𝐺00 = -𝑎-2[∇2𝛷 - 3𝓗(𝛷ʹ + 𝓗𝛹)],
Since 𝛵00 ≡ -(𝜌̄ + 𝛿𝜌) in (6.33),
(6.111) ∇2𝛷 - 3𝓗(𝛷ʹ + 𝓗𝛹) = 4π𝐺𝑎2𝛿𝜌,
where 𝛿𝜌 ≡ ∑𝑎𝛿𝜌𝑎 is the total density perturbation. Equation (6.111) is the relativistic generalization of the Poisson equation. Inside the Hubble radius-i.e. for Fourier modes with 𝑘 ≫ 𝓗-we have ∣∇2𝛷∣ ≫ 3𝓗∣(𝛷ʹ + 𝓗𝛹)∣, so that (6.111) reduces to ∇2𝛷 ≈ 4π𝐺𝑎2𝛿𝜌, which is the Poisson equation in the Newtonian limit.The GR corrections in (6.111) start to become important on scales comparable to the Hubble radius.
Next, we consider the purely spatial part of the Einstein equation,
(6.112) 𝐺𝑖𝑗 = 𝑔𝑖𝑘𝐺𝑘𝑗 = 𝑔𝑖𝑘[𝑅𝑘𝑗 - 1/2 𝑔𝑘𝑗𝑅] = 𝑎-2(1 + 2𝛷)𝛿𝑖𝑘𝑅𝑘𝑗 - 1/2 𝛿𝑖𝑗𝑅,
We will first focus on the tracefree part of 𝐺𝑖𝑗 which is sourced by the anisotropic stress 𝛱𝑖𝑗. Using (6.102) this gives [RE (6.5)(6.9)(6.33)]
(6.113) ∂⟨𝑖∂𝑗⟩(𝛷 - 𝛹) = 8π𝐺𝑎2𝛱𝑖𝑗. [verification needed]
With the replacement ∂⟨𝑖∂𝑗⟩ → -𝑘𝑖𝑘𝑗 and 𝛱𝑖𝑗 = -(𝜌̄ + 𝑃̄)𝑘̂𝑖𝑘̂𝑗, [RE (6.39)] the corresponding equation in Fourier space reads
(6.114) 𝑘2(𝛷 - 𝛹) = 8π𝐺𝑎2(𝜌̄ + 𝑃̄)𝛱,
where 𝛱 ≡ ∑𝑎𝛱𝑎. On large scales, dark matter and baryons can be described as perfect fulids with negligible anisotropic stress. Photons only start to develope an anisotropic stress component during the matter-dominated era when their energy density is subdominant. The only relevant source in (6.113) are free-streaming nutrinos. To describe the neutrino-induced anisotropic stress requires beyond the fluid approximation; see Appendix B. The effect is relatively small, so to the level of accuracy here it can be ignored. Then (6.113) implies 𝛷 ≈ 𝛹.
The time-space part of the Einstein equation equation is obtained in the same way.
(6.115) 𝐺0𝑖 = 𝑔0𝜇𝐺𝜇𝑖 = 𝑔00𝑅0𝑖 = -𝑎-2𝑅0𝑖 = -2𝑎-2∂𝑖(𝛷ʹ + 𝓗𝛹).
Comparing this to 𝛵0𝑖 = ∂𝑖𝑞 in (6.33),
(6.116) 𝛷ʹ + 𝓗𝛹 = -4π𝐺𝑎2𝑞.
With this, the Poisson equation (6.111) can be written as
(6.117) ∇2𝛷 = 4π𝐺𝑎2𝜌̄∆, [verification needed]
where the comoving density contrast ∆ was defined in (6.52). We see that in terms of the comoving density contrast the relativistic generalization of the Poisson equation takes the same form as in /Newtonian treatment, but is now valid on all scales. This will allow us to relate solutions for the gravitational potential directly to the solutions for the dominant source of matter perturbations.
Finally, we look at the trace of space-space Einstein equation as follows
(6.118) 𝛷ʺ + 1/3 ∇2(𝛹 - 𝛷) + (2𝓗ʹ + 𝓗2)𝛹 + 𝓗𝛹ʹ + 2𝓗𝛷ʹ = 4π𝐺𝑎2𝛿𝑃,
where 𝛿𝑃 ≡ ∑𝑎𝛿𝑃𝑎. Assuming 𝛹 ≈ 𝛷, this reduces to
(6.119) 𝛷ʺ + 3𝓗𝛷ʹ + (2𝓗ʹ + 𝓗2)𝛷 = 4π𝐺𝑎2𝛿𝑃,
which becomes a closed equation for the evolution of 𝛷 if we write 𝛿𝑃 = 𝑐𝑠2𝛿𝜌 and use the Poisson equation to relate 𝛿𝜌 to 𝛷.
Exercise 6.8 Derive (6.118).
Summary
The linearized Einstein equations are
(6.120) ∇2𝛷 - 3𝓗(𝛷ʹ + 𝓗𝛹) = 4π𝐺𝑎2𝛿𝜌,
(6.121) -(𝛷ʹ + 𝓗𝛹) = 4π𝐺𝑎2𝑞,
(6.122) ∂⟨𝑖∂𝑗⟩(𝛷 - 𝛹) = 8π𝐺𝑎2𝛱𝑖𝑗,
(6.123) 𝛷ʺ + 𝓗𝛹ʹ + 2𝓗𝛷ʹ + 1/3 ∇2(𝛹 - 𝛷) + (2𝓗ʹ + 𝓗2)𝛹 = 4π𝐺𝑎2𝛿𝑃.
In the absence of anisotropic stress, 𝛱 ≈ 0, (6.122) implies that the two metric potentials are equal, 𝛷 ≈ 𝛹, and (6.123) reduces to
(6.124) 𝛷ʺ + 3𝓗𝛷ʹ + (2𝓗ʹ + 𝓗2)𝛷 = 4π𝐺𝑎2𝛿𝑃.
Equation (6.120) and (6.121) can be combined into ∇2𝛷 = 4π𝐺𝑎2𝜌̄∆, which has same form as Newtonian Poisson equation, but is now valid on all scale.
Combing the Einstein equations with the conservation equations (6.91) and (6.92) leads to a closed system of equation (after specifying the equation of state and the sound speed of each fluid component). We will study the solutions of these equations for various situation.
6.2 Initial Conditions
At sufficiently early times, all scales of interest to current observations were outside of Hubble radius. On such superhorizon scales, the evolution of the perturbations becomes very simple, especially for adiabatic initial conditions.
6.2.1 Superhorizon Limit
Consider the superhorizon limit of the continuity equations (6.85) and (6.88) for matter and radiation:
(6.125) 𝛿ʹ𝑚 = 3𝛷ʹ,
(6.126) 𝛿ʹ𝑟 = 4𝛷ʹ,
where the fact that the velocity terms can be dropped follows from the superhorizon limit of the Euler equations (6.83) and (6.86). Integrating these equations for photons, neutrinos, baryons and cold dark matter gives
(6.127) 𝛿𝑟 = 4𝛷 + 𝐶𝑟 → 𝛿𝑟 = 4𝛷 + 𝐶𝑟
𝛿𝜈 = 4𝛷 + 𝐶𝜈 → 𝛿𝜈 = 𝛿𝑟 + 𝑆𝜈
𝛿𝑐 = 3𝛷 + 𝐶𝑐 → 𝛿𝑐 = 3/4 𝛿𝑟 + 𝑆𝑐
𝛿𝑏 = 3𝛷 + 𝐶𝑏 → 𝛿𝑏 = 3/4 𝛿𝑟 + 𝑆𝑏
where 𝐶𝑎's are integration constants. Note that these constants are function of the wavevecter 𝐤 in general. 𝑆𝑎's (for 𝑎 = 𝜈, 𝑐, 𝑏) are called isocurvature modes.
A preferred set of initial conditions are given by the adiabatic mode with 𝑆𝜈 = 𝑆𝑐 = 𝑆𝑏 = 0 and 𝐶𝑟 ≠ 0. In that case, the initial values of all perturbations are determined by a single degree of freedom. We will assume adiabatic initial conditions throughout the the rest of this book and these also seems to be preferred by observations (see Section 8.4.1).
Next, we look at the Einstein equation (6.120):
(6.128) ∇2𝛷 - 3𝓗(𝛷ʹ + 𝓗𝛹) = 4π𝐺𝑎2(𝜌̄𝛾𝛿𝛾 + 𝜌̄𝜈𝛿𝜈 + 𝜌̄𝑐𝛿𝑐 + 𝜌̄𝑏𝛿𝑏),
where we ignored the anisotropic stress of the neutrinos, so that 𝛷 ≈ 𝛹. On large scale, we can drop ∇2𝛷 and at the early times the matter contributions are negligible,
(6.129) 3𝓗(𝛷ʹ + 𝓗𝛹) = -4π𝐺𝑎2(𝜌̄𝛾𝛿𝛾 + 𝜌̄𝜈𝛿𝜈).
Specializing to adiabatic initial conditions, we have 𝛿𝛾 = 𝛿𝜈 and 4π𝐺𝑎2(𝜌̄𝛾𝛿𝛾 + 𝜌̄𝜈𝛿𝜈) = 3𝓗2/2. [RE (2.516)] Substituting 𝓗 = 1/𝜂, [In radiation-domonated era, 𝑎 ∝ 𝜂 according to (2.149), so 𝓗 = 𝑎ʹ/𝑎 = 𝜂ʹ/𝜂 = 1/𝜂.]
(6.130) 𝜂𝛷ʹ + 𝛷 = -1/2 𝛿𝛾.
Taking a time derivative, and using (6. 126) to replace to 𝛿ʹ𝑟, this becomes
(6.131) 𝜂𝛷ʺ + 4𝛷ʹ = 0. [(𝜂𝛷ʹ)ʹ + 𝛷ʹ = -1/2 𝛿ʹ𝛾 ⇒ 𝛷ʹ + 𝜂𝛷ʺ + 𝛷ʹ = -1/2 4𝛷ʹ ⇒ 𝜂𝛷ʺ + 4𝛷ʹ = 0.]
The two solutions to this equation are the growing mode 𝛷 = const and decaying mode 𝛷 ∝ 𝜂-3. [𝛷 = const or 𝑐1/𝜂3 + 𝑐2.] Growing mode 𝛷 = 𝛷𝑖 in (6.130) implies
(6.132) 𝛿𝛾(𝜂𝑖, 𝐤) = -2𝛷𝑖(𝐤).
We see then that the integration constant in (6.127) is fixed by the primordial value 𝐶𝑟 = -6𝛷𝑖. For adiabatic fluctuations in all components are then related as
(6.133) 𝛿𝑟 = 𝛿𝜈 = 4/3 𝛿𝑐 = 4/3 𝛿𝑏 = - 2𝛷𝑖 (superhorizon).
Gauge dependence One important subtlety is the gauge dependence of the superhorizon dynamics. Considr the Poisson equation written in terms of the comoving density contrast
(6.134) ∆ = - 2/3 𝑘2/𝓗2 𝛷.
First, the comoving density contrast ∆ is much smaller than 𝛿 on superhorizon scales. Second, it evolves as ∆ ∝𝓗-2 ∝ 𝜂2. So on superhorizon scale, we don't have to worry about the qualitative difference in the two different gauges and we cannot measure the density contrast! On subhorizon scale we instead have for our observation
(6.135) (∆ - 𝛿)/∆ = - 3/4 𝓗(𝛷ʹ + 𝓗𝛷)/𝑘2𝛷 →(𝑘 ≫ 𝓗)→ 0,
so that there is no difference between ∆ and 𝛿 on small scales. This is a general feature: the gauge problem disappear for all measureable quantities on subhorizon scales.
Had we taken the anisotropic stress due to the neutrinos into account, we would instead have found (see Problem 6.2)
(6.136) 𝛿𝛾(𝜂𝑖, 𝐤) = -2𝛹𝑖(𝐤) = -2𝛷𝑖(𝐤)(1 + 2/5 𝑓𝜈)-1,
where we have introduced the fractional neutrino density 𝑓𝜈 ≡ 𝜌𝜈/(𝜌𝜈 + 𝜌𝛾).
Exercise 6.9 Using the result from Chapter 3, show that
(6.137) 𝑓𝜈 ≈ 0.41,
so that 𝛹𝑖 ≈ 0.86 𝛷𝑖.
[Solution] Since 𝜌𝜈 = 7/8 𝑁eff (4/11)4/3𝜌𝛾 [RE (3.66)]
(a) 𝑓𝜈 ≡ 𝜌𝜈/(𝜌𝜈 + 𝜌𝛾) = 7/8 𝑁eff (4/11)4/3/(7/8 𝑁eff (4/11)4/3 + 1) ≈ 0.41.
where 𝑁eff = 3.046. [RE p.88] From (6.136)
(b) 𝛹𝑖 = 𝛷𝑖(1 + 2/5)-1 ≈ 0.86. ▮
6.2.2 Adiabatic Perturbations
Adiabatic perturbations can be created by starting with a homogeneous universe and performing a common, local shift in time of all background quantities, 𝜂 → 𝜂 + π(𝑡, 𝐱). After this time shift, some parts of the universe are "ahead" and others are "behind" in the evolution. As we will see in Chapter 8, quantum fluctuations during inflation produce precisely such a time shift in the background quantities. The induced pressure and density perturbations are
(6.138) { 𝛿𝑃𝑎(𝑡, 𝐱) = 𝑃̄𝑎ʹπ(𝑡, 𝐱), 𝛿𝜌𝑎(𝑡, 𝐱) = 𝜌̄𝑎ʹπ(𝑡, 𝐱) ⇒ { 𝛿𝑃𝑎/𝛿𝜌𝑎 = 𝑃̄𝑎ʹ/𝜌𝑎ʹ, 𝛿𝜌𝑎/𝛿𝜌𝑏 = 𝜌̄𝑎ʹ/𝜌̄𝑏ʹ
where we used that π(𝑡, 𝐱) is the same for all species 𝑎. The first relation on the right implies
(6.139) 𝛿𝑃𝑎 = 𝑐2𝑠,𝑎𝛿𝜌𝑎,
so that the perturbations are indeed adiabatic in the sense defined in (6.98). Referring to similar equation (2.106), using 𝜌̄𝑎ʹ = -3𝓗(1 + 𝜔𝑎)𝜌̄𝑎, the the second relation on the right can be written as
(6.140) 𝛿𝑎/(1 + 𝜔𝑎) = 𝛿𝑏/(1 + 𝜔𝑏) for all species 𝑎 and 𝑏.
Perturbations in matter (𝜔𝑚 = 0) and radiation (𝜔𝑟 = 1/3) obey
(6.141) 𝛿𝑚 = 3/4 𝛿𝑟,
which is the same relation as for adiabatic mode in (6.127). An important corollary is that 𝛿𝜌 ≡ ∑𝑎𝜌̄𝑎𝛿𝑎 is dominated by the species that carries the dominant energy density, 𝜌̄𝑎 since all of the 𝛿𝑎's are comparable.
Finally, we note that the time shift ʹπ(𝑡, 𝐱) has the interpretation of the Goldstone boson associated with spontaneous breaking of time translation symmetry. This symmetry breaking arises because of the time dependence of the cosmological background. The language of spontaneous symmetry breaking has recently become very popular for describing cosmological perturbations and an effective field theory was constructed in terms of the Goldstone mode [7].
Exercise 6.10 Show that the thermodynamic relation 𝛵𝑑𝑆/𝑉 = 𝑑𝑈 + 𝑃𝑑𝑉 implies
(6.142) 𝛵𝑑𝑆/𝑉 = [𝜌𝜈 - 3/4 𝑟𝜈(𝜌 + 𝑃)](𝛿𝜈 - 𝛿𝛾) + ∑𝑎=𝑐,𝑏[𝜌𝑎 - 𝑟𝑎(𝜌 + 𝑃)](𝛿𝜈 - 3/4 𝛿𝛾).
where 𝑟𝑎 ≡ 𝑛𝑎/𝑛 are the fractional number densities of the species. For adiabatic perturbations, this means that 𝑑𝑆 = 0.
6.2.3 Isocurvature Perturbations*
The complement of adiabatic perturbation are isocurvature perturbations. For two component 𝑎 and 𝑏, the (density) isocurvature perturbation is
(6.143) 𝑆𝑎𝑏 ≡ 𝛿𝑎/(1 + 𝜔𝑎) - 𝛿𝑏/(1 + 𝜔𝑏),
We see from (6.140) that a nonzero value of this quantity measures the deviation from the adiabatic mode. Special cases of this isocurvature mode are given in (6.127). The "isocurvature" was introduced because these perturbations can be chosen in such a way that the curvature perturbation 𝜁 vanishes. In that case an overdensity in one species compensate for an underdensity in another, resulting in no net curvature perturbation.
Let us illustrate the special case of the neutrino density isocurvature mode. From the definition of 𝜁 in (6.54) we have
(6.144) 𝜁 = 𝛷 - 𝛿𝜌/3(𝜌 + 𝑃) = 𝛷 - (𝑓𝛾𝛿𝛾 + 𝑓𝜈𝛿𝜈 + 𝑓𝑏𝛿𝑏 + 𝑓𝑐𝛿𝑐)/(3 + 𝑓𝛾 + 𝑓𝜈),
where we used the continuity equation for 𝜌̄ʹ[citation needed] and introduced 𝑓𝑎 ≡ 𝜌𝑎/𝜌. At early times, we can ignore byrons and dark matter, 𝑓𝑏,𝑐 ≈ 0, so that 𝑓𝛾 ≈ 1 - 𝑓𝜈 and hence
(6.145) 𝜁 = 𝛷 - 𝛿𝛾/4 + 𝑓𝜈(𝛿𝛾 - 𝛿𝜈)/4 = - 1/4 (𝐶𝛾 + 𝑓𝜈𝑆𝜈),
where we used (6.127). The curvature perturbation vanishes for 𝑆𝜈 = -𝐶𝛾/𝑓𝜈 and the relation between the density contrast is
(6.146) 𝛿𝛾 = 4𝛷 - 𝑓𝜈𝑆𝜈 = 𝛿𝜈 - 𝑆𝜈 = 4/3 𝛿𝑐 = 4/3 𝛿𝑏.
In Problem 6.2 we will show that
(6.147) 𝑆𝜈 = (15 + 4𝑓𝜈)/(1 - 𝑓𝜈) 𝛷𝑖 ≈ 68.8 𝛷𝑖, where the final equality is for 𝑓𝜈 ≈ 0.41.
There are many different types of isocurvature perturbation. The general pheonomenology of isocurvature perturvations is described in [8]. Because isocurvature perturbations have not been seen in CMB data, adiabatic initial conditions are preferred. They are also attractive on theoretical grounds, because adiabatic perturbations arise naturally in the simplest inflationary models (see Chapter 8) and are frozen on superhorizon scales (see Section 6.2.4). The latter property is important for the predictive power of inflation as it allows us to be agnostic about the uncertain physics of reheating. But primordial isocurvature perturbations can be washed out by thermal equilibrium and their amplitude is strongly model-dependent and sensitive to the post-inflationary evolution. If all particle species are in thermal equilibrium after inflation and their local densities are determined by the temperature (with vanishing chemical potential) the the primordial perturbations are adiabatic. For instance, the neutrino density isocurvature mode discussed above could be due to spatial fluctuations in the chemical potential of neutrinos.
Given the complexity of models with isocurvature fluctuations and the fact that observations don't seem to require them, we will assume adiabatic initial conditions for the rest of this book.
6.2.4 Curvature Perturbations
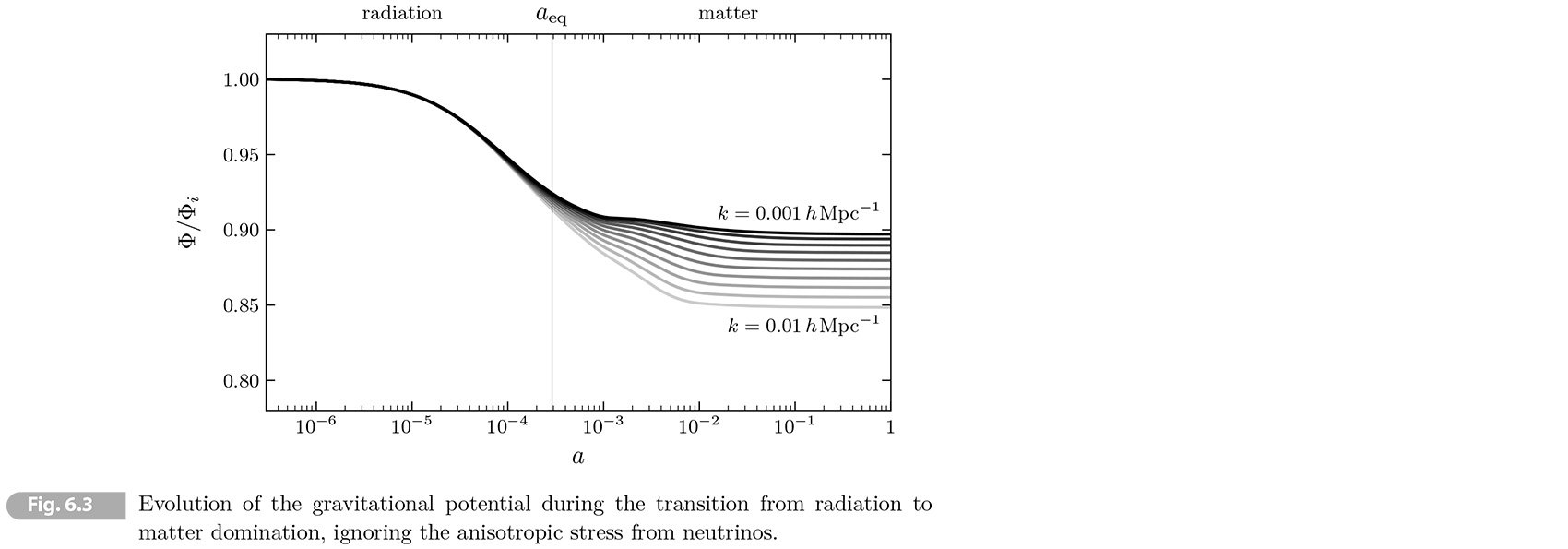
Fig. 6.3 shows the superhorizon evolution of gravitational in the transition from radiation domination to matter domination. We see that the gravitational potential is a constant during the radiation and matter eras, but varies inbetween.
Exercise 6.11 Consider a universe dominated by a fluid with constant equation of state 𝜔 ≠ -1. Assuming adiabatic perturbations and vanishing anisotropic stress, show that the evolution of the gravitational potential obeys
(6.148) 𝛷ʺ + 3(1 + 𝜔)𝓗𝛷ʹ - 𝜔∇2𝛷 = 0.
[Solution] Ignoring anisotropic stress, the linearlized Einstein equation is
(a) 𝛷ʺ + 3𝓗𝛷ʹ + (2𝓗ʹ + 𝓗2)𝛷 = 4π𝐺𝑎2𝛿𝑃.
(b) 4π𝐺𝑎2𝛿𝑃 = 4π𝐺𝑎2 𝜔𝛿𝜌 = 𝜔[∇2𝛷 - 3𝓗(𝛷ʹ + 𝓗𝛷)]
(c) 2𝓗ʹ + 𝓗2 = -2[4π𝐺/3 (𝜌 +3𝜔𝜌)]𝑎2 + (8π𝐺/3 𝜌)𝑎2 = -3𝜔(8π𝐺/3 𝑎2) = -3𝜔𝓗2
(d) 𝛷ʺ + 3(1 + 𝜔)𝓗𝛷ʹ - 𝜔∇2𝛷 = 0. ▮
This shows that the growing mode is a constant on superhorizon scales.
It would be convenient to identify an alternative perturbation variable that stays constant on large scales even the equation of state changes. This is particularly important for the transition from inflation to the radiation-dominated universe. Since the equation of state during reheating is unknown. it is crucial that we can track a quantity whose evolution doesn't depend on these details. This will allow us to match the predictions made by inflation to the fluctuations in the primordial plasma after inflation. For adiabatic initial conditions, the conserved perturbations are the crucial that we can track a quantity whose devolution doesn't depend on details. This will allow us to match the predictions made by inflation to the fluctuations in the primordial plasma after inflation. For adiabatic initial conditions, the conserved perturbations are the curvature perturbations introduced in (6.54) and (6.55) in Newtonian gauge
(6.149-50) 𝜁 = 𝛷 - 𝛿𝜌/3(𝜌̄ + 𝑃̄), 𝓡 = 𝛷 - 𝓗𝑣, [verification needed]
where we use the continuity equation to replace 𝜌̄ʹ. To prove that 𝜁 is indeed conserved on super-Hubble scale we take the time derivative of (6.149):
(6.151) 𝜁ʹ = 𝛷ʹ - 𝛿𝜌ʹ/3(𝜌̄ + 𝑃̄) + (𝜌̄ʹ + 𝑃̄ʹ)/3(𝜌̄ʹ + 𝑃̄ʹ)2 𝛿𝜌.
Using continuity equations [RE (2.106)]
(6.152) 𝜌̄ʹ = -3𝓗(𝜌̄ + 𝑃̄), 𝛿𝜌ʹ = -3𝓗(𝛿𝜌 + 𝛿𝑃) - ∂𝑖𝑞𝑖 + 3𝛷ʹ(𝜌̄ + 𝑃̄), we get
(6.153) (𝜌̄ + 𝑃̄)𝜁ʹ/𝓗 = (𝛿𝑃 - 𝑃̄ʹ/𝜌̄ʹ 𝛿𝜌) + 1/3 ∂𝑖𝑞𝑖/𝓗.
For adiabatic perturbations, the term in brackets on the right-hand side vanishes, while ∂𝑖𝑞𝑖 = ∇2𝑞 is suppressed by a factor of 𝑘2/𝓗2 on large scales, so that 𝜁ʹ/𝓗 →(𝑘 ≪ 𝓗)→ 𝑂(𝑘2/𝓗2) ≈ 0. We have therefore established the conservation of the curvature perturbation on superhorizon scales.
Exercise 6.12 Show that the comoving curvature perturbation satisfies
(6.154) (𝜌̄ + 𝑃̄)𝓡ʹ/𝓗 = (𝛿𝑃 - 𝑃̄ʹ/𝜌̄ʹ 𝛿𝜌) + 𝑃̄ʹ/𝜌̄ʹ ∇2𝛷/4π𝐺𝑎2,
and is therefore also conserved on superhorizon scales. Of course, this had to be true since we showed in (6.59) that 𝓡 is equal to 𝜁 on large scales.
Exercise 6.13 Consider a universe dominated by a fluid with constant equation of state. Show that the superhorizon limit of the curvature perturbation is
(6.155) 𝓡 →(𝑘 ≪ 𝓗)→ (5 + 3𝜔)/(3 + 3𝜔) 𝛷.
Use this to show that the amplitude of super-Hubble modes of 𝛷 drops by a factor of 9/10 in the radiation-to-mater transition (as seen in Fig. 6.3).
[Solution] Consider the curvature perturbation equation 𝜁 and a constant equation of state 𝜔 induce
(a) 𝜁 = 𝛷 - 𝛿𝜌/3(𝜌 + 𝑃) →(𝑘 ≪ 𝓗)→ 𝜁 = 𝛷 - 𝛿/3(1 + 𝜔)
On superhorizon scales we have 𝛿 = -2𝛷 and hence
(b) 𝓡 ≈ 𝜁 = 𝛷 + 2𝛷/3(1 + 𝜔) = (5 + 3𝜔)/(3 + 3𝜔) 𝛷.
In the radiation and matter eras, 𝜔 = 1/3 and 0, respectively
(c) 𝓡 = { 3/2 𝛷RD, 5/3 𝛷MD
(d) since 𝓡 = const, 3/2 𝛷RD = 5/3 𝛷MD ⇒ 𝛷MD = 9/10 𝛷RD. ▮
6.2.5 Primordial Power Spectrum
Using the result of Exercise 6.13, the superhorizon value of the gravitational potential during the radiation era is
(6.156) 𝛷(𝜂, 𝐤) = 2/3 𝓡𝑖(𝐤) (superhorizon),
where 𝓡𝑖 ≡ 𝓡(0, 𝐤) is the initial value of the conserved curvature perturbation. Ignoring the effect of neutrinos, so that 𝛹 ≈ 𝛷, and assuming adiabatic initial conditions, we then also have
(6.156) 𝛿𝑟 = 4/3 𝛿𝑚 = -2𝛷 = -4/3 𝓡𝑖 (superhorizon),
The initial amplitudes of all fluctuations are determined by 𝓡𝑖. We take the power spectrum of the primordial curvature perturbation to be
(6.157) 𝒫𝓡(𝑘, 𝑡𝑖) = 𝛢𝑘𝑛,
where 𝛢 and 𝑛 are constants. In Chapter 8, we will show that inflation naturally predicts a nearly scale-invariant spectrum, with 𝑛 ≈ 1.
|
|
|





































