|
김관석
|
2024-08-18 20:38:36, 조회수 : 175 |
- Download #1 : BC_2b.jpg (112.1 KB), Download : 2

2.3 Dynamics
So far, we have used the symmetries of the universe to fix its geometry and studied the propagation of particles in the expending spacetime. The scale factor 𝑎(𝑡) has remained an unspecified function of time. The evolution of the scale factor follows from the Einstein equation
(2.84) 𝐺𝜇𝜈 ( + 𝛬𝑔𝜇𝜈) = 8π𝐺/𝑐4 𝑇𝜇𝜈, [𝛬: cosmological constant, 𝑔𝜇𝜈:metric tensor]
where 𝐺 = 6.67 × 10-11 m3 kg-1 s-2 is Newton's constant. This relates the Einstein tensor 𝐺𝜇𝜈 (a measure of the "spacetime curvature" of the universe) to the energy-momentum tensor 𝑇𝜇𝜈 (a measure of "matter content" of the universe). We will first discuss the possible forms of cosmological energy-momentum tensors, then compute the Einstein tensor for FRW background, and finally put them together to solve for the evolution of the scale factor 𝑎(𝑡) as a function of the matter content.
2.3.1 Perfect Fluids
We have seen how the spacetime geometry of the universe is constrained by homogeneity and isotropy. Now, we will determine which types of matter are consistent with these symmetries. We will find that the coarse-grained energy-momentum tensor is required to be that of a perfect fluid.
(2.85) 𝑇𝜇𝜈 = (𝜌 + 𝑃/𝑐2)𝑈𝜇𝑈𝜈 + 𝑃𝑔𝜇𝜈,
where 𝜌𝑐2 and 𝑃 are the energy density and pressure in the rest frame of the fluid, and 𝑈𝜇 is its 4-velocity relative to a comoving observer. {Wikipedia Perfect fluid: Stress-energy tensor of a perfect fluid in the rest frame diag(𝜌𝑐2, 𝑝, 𝑝, 𝑝)]
Number density
Let us a simpler object: the number current 4-vector 𝑁𝜇. 𝑁0 measures the number density particles, where a "particle" in cosmology may be an entire galaxy. 𝑁𝑖 is the flux of particle in the direction 𝑥𝑖. We call 𝑁0 a three scalar because its value doen't change under a purely spatial coordinate transformation. But 𝑁𝑖 transforms like a 3-vector under such a transformation. We want to determine which form of the number current is consistent with the homogeneity and isotropy seen by a comoving observer.
Isotropy requires that the mean value of any 3-vector, such as 𝑁𝑖, must vanish, and homogeneity require that the mean value of 3-scalar such as 𝑁0, is only a function of time. Hence
(2.86) 𝑁0 = 𝑐𝑛(𝑡), 𝑁𝑖 = 0,
where 𝑛(𝑡) is the number of galaxies per proper volume. A general observer (i.e. an observer in motion relative to the men rest frame of the particles), would measure the following number current 4-vector
(2.87) 𝑁𝜇 = 𝑛𝑈𝜇,
where 𝑈𝜇 ≡ 𝑑𝑥𝜇/𝑑𝜏 is relative 4-velocity between particles and the observer. We recover (2.86) for a comoving observer, with 𝑈𝜇 = (𝑐, 0, 0, 0). Moreover, for 𝑈𝜇 = 𝛾(𝑐, 𝑣𝑖, the expression (2.87) gives the correctly boosted result, where 𝛾 is the Lorentz factor for the fact that one of the dimensions is Lorentz contracted.
How does the number density evolve with time? If the number of particles is conserved, then the rate of of change of number density must equal the divergence of the flux of particles. In Minkowski space, this imply the following continuity equation ∂0𝑁0 = -∂𝑖𝑁𝑖, or in relativistic notation,
(2.88) ∂𝜇𝑁𝜇 = 0.
Equation (2.89) is generalized to curved spacetimes by replacing the partial derivative with a covariant derivative (see Appendix A)
(2.89) ∇𝜇𝑁𝜇 = 0.
This covariant form of the continuity equation is valid independent of the choice of coordinates.
Covariant derivative The covariant derivative is an important object in differential geometry and it is fundamental importance in general relativity. But we will not get into these detail here and simply tell us that how the covariant derivatives acts on 4-vectors with upstairs and downstairs indices:
(2.90-91) ∇𝜇𝐴𝜈 = ∂𝜇𝐴𝜈 + 𝑁𝜇, ∇𝜇𝛣𝜈 = ∂𝜇𝛣𝜈 - 𝛤𝜆𝜇𝜈𝛣𝜆.
We already encounter (2.91) in our discussion of the geodesic equation in (2.43), [Wikipedia Covariant derivative] The action on a general tensor is straightforward generalization of these two results. For example, the covariant derivative of a rank-2 tensor with mixed indices is
(2.92) ∇𝜇𝛵𝜎𝜈 = ∂𝜇𝛵𝜎𝜈 + 𝛤𝜎𝜇𝜆𝛵𝜆𝜈 - 𝛤𝜆𝜇𝜈𝛵𝜎𝜈.
Using (2.91) in (2.90, we get
(2.93) ∂𝜇𝑁𝜇 = -𝛤𝜇𝜇𝜆𝑁𝜆.
Let us evaluate this in the rest frame of fluid. Substituting the components of the number current in (2.86), we obtain
(2.94) 𝑑𝑛/𝑐 𝑑𝑡 = -𝛤𝜇𝜇0 𝑛 = -3/𝑐 𝑎̇/𝑎 𝑛, [𝑐 𝑑𝑛/𝑐 𝑑𝑡 = -𝛤𝜇𝜇0 𝑐 𝑛]
where we have used that 𝛤000 = 0 and 𝛤𝑖𝑖0 = -3/𝑐 𝑎̇/𝑎. Hence, we find that
(2.95) 𝑛̇/𝑛 = -3𝑎̇/𝑎 ⇒ 𝑛(𝑡) ∝ 𝑎-3 [∫ 𝑛̇/𝑛 𝑑𝑡 = ∫ 1/𝑛 𝑑𝑛 = log(𝑛) + const; ∫ -3𝑎̇/𝑎 𝑑𝑡 = ∫ -3/𝑎 𝑑𝑎 = log(1/𝑎3) + const]
As expected, the number density decreases in proportion to the increase of the proper volumne, 𝑉 ∝𝑎3.
Energy-momentum tensor
We will now use a similar logic to determine which form of the energy-momentum tensor 𝛵𝜇𝜈 is consistent with the requirement of homogeneity and isotropy. First, we decompose 𝛵𝜇𝜈 into a 3-scalar 𝛵00, two 3-vectors 𝛵𝑖0 and 𝛵0𝑗 and a 3-tensor 𝛵𝑖𝑗. The physical meaning of these component is
(2.96) 𝛵𝜇𝜈 = (𝛵00, 𝛵0𝑗, 𝛵𝑖0, 𝛵𝑖𝑗) = (energy density, momentum density, energy flex, stress tensor).
In a homogeneous universe, the energy density must be independent of position, but can depend on time, 𝛵00 = 𝜌(𝑡)𝑐2. Moreover, isotropy again requires the mean values of the 3-vectors in the comoving frame, 𝛵𝑖0 = 𝛵0𝑗 = 0. Finally isotropy around a point 𝐱 = 0 constrains the mean value of 3-tensor, such as 𝛵𝑖𝑗, to be proportional to 𝛿𝑖𝑗. Since the metric 𝑔𝑖𝑗 equals 𝑎2𝛿𝑖𝑗 at 𝐱 = 0, we have
(2.97) 𝛵𝑖𝑗(𝐱 = 0) ∝ 𝛿𝑖𝑗 ∝ 𝑔𝑖𝑗(𝐱 = 0).
Homogeneity requires the proportionality coefficient to be only a function of time. Moreover, Since this is a proportionality between two tensors, 𝛵𝑖𝑗 and 𝑔𝑖𝑗, it remains unaffected by transformation of the spatial coordinates, including those transformations that preserve the form of 𝑔𝑖𝑗 while taking this origin into any other point. Hence homogeneity and isotropy require the component s of energy-momentum tensor everywhere to take the form
(2.98) 𝛵00 ≡ 𝜌(𝑡)𝑐2, 𝛵𝑖0 ≡ 𝑐𝜋𝑖 = 0, 𝛵𝑖𝑗 = 𝑃(𝑡)𝑔𝑖𝑗(𝑡, 𝐱).
Raising one of indices, we find [for example?]
(2.99) 𝛵𝜇𝜈 = 𝑔𝜇𝜈𝛵𝜇𝜈 = diag(-𝜌𝑐, 𝑃, 𝑃, 𝑃).
which we recognize as the energy-momentum tensor of a perfect fluid in the frame of a comoving observer. More generally, the energy-momentum tensor can be written in the following, explicitly covariant, form [RE (2.84)]
(2.100) 𝑇𝜇𝜈 = (𝜌 + 𝑃/𝑐2)𝑈𝜇𝑈𝜈 + 𝑃𝑔𝜇𝜈
where 𝑈𝜇 is the relative 4-velocity between the fluid and the observer. We can recover (2.98) for a comoving observer, 𝑈𝜇 = (𝑐, 0, 0, 0). [Why not 𝑈𝜇?]
Continuity equation
In Minkowski space energy and momentum are conserved. The energy density therefore satisfied the continuity equation ῤ = -∂𝑖π𝑖, i.e. the rate of change of the density equals the divergence of the energy flux π. Similarly the evolution of momentum satisfies the Euler equation 𝑑π𝑖/𝑑𝑡 = ∂𝑖𝛲. These conservation laws can be combined into a 4-component conservation equation for the energy-momentum tensor [Wikipedia Continuity equation: and Euler equations (fluid dynamics):]
(2.101) ∂𝜇𝑇𝜇𝜈 = 0.
In GR this id promoted to the covariant conservation equation
(2.102) ∇𝜇𝑇𝜇𝜈 = 0.
Using (2.92)
(2.103) ∇𝜇𝑇𝜇𝜈 = ∂𝜇𝛵𝜇𝜈 + 𝛤𝜇𝜇𝜆𝛵𝜆𝜈 - 𝛤𝜆𝜇𝜈𝛵𝜇𝜆 = 0.
This corresponds to four separate equation (𝜈: 0~3). The evolution of the energy density is determined by the 𝜈 = 0 equation
(2.104) ∂𝜇𝛵𝜇0 + 𝛤𝜇𝜇𝜆𝛵𝜆0 - 𝛤𝜆𝜇0𝛵𝜇𝜆 = 0.
Since 𝛵𝑖0 vanishes by isopropy, this reduces to [∂𝜇𝛵00 + 𝛤𝜇𝜇𝜆𝛵00 - 𝛤𝜆𝜇0𝛵𝜇𝜆 = 0.]
(2.105) 1/𝑐 𝑑(𝜌𝑐2)/𝑑𝑡 + 𝛤𝜇𝜇0(𝜌𝑐2) - 𝛤𝜆𝜇0𝛵𝜇𝜆 = 0,
where 𝛤𝜆𝜇0 vanishes unless 𝜆 and 𝜇 are spatial indices 𝑖 and they are same, i.e. 𝜆 = 𝜇 = 𝑖. So we have 𝛤𝑖𝑖0 = 3𝑐-1 𝑎̇/𝑎. [RE (2.45) and 𝛵𝜇𝜆 = 𝛵𝑖𝑖 = 𝑃.] The continuity equation (2.105) then becomes
(2.106) 𝜌̇ + 3 𝑎̇/𝑎 (𝜌 + 𝑃/𝑐2) = 0. [𝑐 𝑑𝜌/𝑑𝑡 + 3𝑐 𝑎̇/𝑎 (𝜌 + 𝑃/𝑐2) = 0.]
This important equation describes "energy conservation" in the cosmological context. Notice that the usual notion of energy conservation in flat space relies on a symmetry under the translations. This symmetry is broken in an expanding space, so the familiar energy conservation does not have to hold and is replaced by (2.106).
Exercise 2.4 Show that (2.106) can be obtain from the thermodynamic relation 𝑑𝑈 = -𝑃𝑑𝑉, where 𝑈 = (𝜌𝑐2)𝑉 and 𝑉 ∝𝑎3.
[Solution] Using 𝑈 = (𝜌𝑐2)𝑉, we have 𝑑𝑈 = 𝑐2𝑉(𝑑𝜌 + 𝜌 𝑑𝑉/𝑉) and with 𝑑𝑈 = -𝑃𝑑𝑉 becomes the following and then we used 𝑉 ∝𝑎3 in the final equality.
(a) 𝑑𝜌 = - 𝑑𝑉/𝑉(𝜌 + 𝑃/𝑐2) = -3 𝑑𝑎/𝑎 (𝜌 + 𝑃/𝑐2),
(b) (𝜌 + 𝑃/𝑐2) log 𝑉 + const = (𝜌 + 𝑃/𝑐2) log 𝑎3 + const)
By taking a derivative to time 𝑡 we get the continuity equation,
(c) 𝑑𝜌/𝑑𝑡 = -3 𝑎̇/𝑎 (𝜌 + 𝑃/𝑐2). ⇒ 𝜌̇ + 3 𝑎̇/𝑎 (𝜌 + 𝑃/𝑐2) = 0. ▮
Most cosmological fluids can be parameterized in terms of a constant equation of state, 𝜔 = 𝛲/(𝜌𝑐2). In that case, we get
(2.107) 𝜌̇/𝜌 = -3(1 + 𝜔) 𝑎̇/𝑎 ⇒ 𝜌 ∝ 𝑎-3(1 + 𝜔) [∫ 𝜌̇/𝜌 𝑑𝑡 = log(𝜌) + const; ∫ [-3(1 + 𝜔) 𝑎̇/𝑎] 𝑑𝑡 = log[𝑎-3(1 + 𝜔)] + const]
which shows how the dilution of the energy density depends on the equation of state.
2.3.2 Matter and Radiation
The term matter will be used to refer to a fluid whose pressure is much smaller than its energy density, ∣𝛲∣≪ 𝜌𝑐2. As we will see in Chapter 3, this is the case for a gas of non-relativistic particles, for which the energy density is dominated by their rest mass. Setting 𝜔 = 0 in (2.107) gives
(2.108) 𝜌 ∝ 𝑎-3.
This dilution of the energy density simply reflects that the fact the volume of a region of space increases as 𝑉 ∝ 𝑎3, while the energy within the region stays constant.
• Baryons Cosmologists refers to ordinary matter (nuclei and electrons) as baryons.Electrons are leptons, but nuclei are so much heavier than electrons that most of the mass is in this baryons.
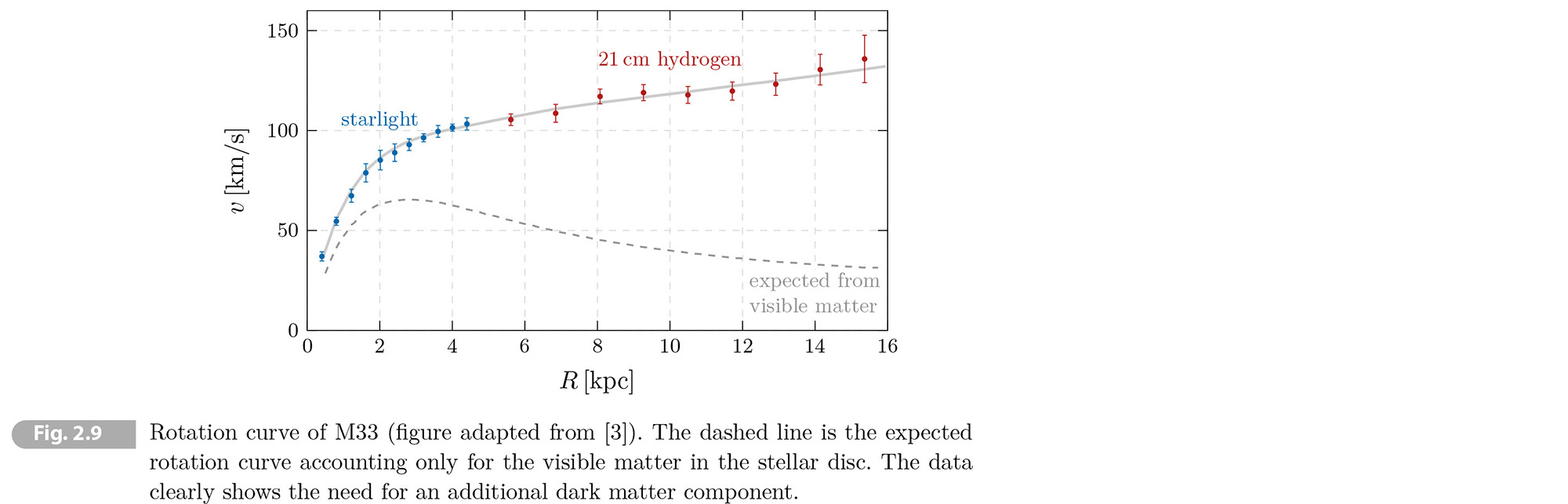
• Dark Matter Most of the matter in the universe is in the form of dark matter. Figure 2.9 shows the orbital speeds of visible stars or gas in the galaxy M33 versus their radial distance from the center of the galaxy. We see that the rotation speeds stay constant for behind the extent of the visible disc. This suggests that there is an invisible halo of dark matter that holds the galaxy together. On larger scale, dark matter has been detected by gravitational lensing. As the CMB photons travel through the universe they get deflected by the total matter in the universe. The effect can be measured statistically and provides one of the best pieces of evidence for dark matter on a cosmic scale.
The precise nature of the dark matter is unknown. We usually think of it as a new particle species, but we don't know what it really is. There are many popular dark matter candidates such as WIMPs, axions, MACHOs, and primordial black holes. [Wikipedia Dark matter:] Wile finding a microscopic detail don't affect the large-scale evolution of the universe. On large scales, all dark matter models are described by the same pressureless fluid. This cold dark matter (CDM) is an integral part of the standard model of cosmology.
The term radiation will be used to denote for which the pressure is on third of the energy density, 𝛲 = 1/3 𝜌𝑐2. This is the case for a gas of relativistic particles, for which the energy density to dominated by the kinetic energy. Setting 𝜔 = 1/3 in (2.107) gives
(2.109) 𝜌 ∝ 𝑎-4.
The dilution now includes not just the expansion, 𝑉 ∝ 𝑎3, but also the redshifting of the energy of the particles, 𝐸 ∝ 𝑎-1.
• Light particles At early times, all particles of the Standard Model acted as relativistic, because the temperature of the universe was larger than the masses of the particles. As the temperature of the universe dropped, the massless of many particles became relevant and they started behave like matter.
• Photons Being massless, photons are always relativistic. Together with neutrinos, they ere the dominant energy density during Big Bang nucleosynthesis. Today, we observe these photons in the form of the CMB.
• Neutrinos For most of history of the universe neutrinos behaves like radiation. Only recently have their small masses become relevant, making them act like matter.
• Gravitons The early universe may also have produced a background of gravitons. The density of these gravitons is predicted to be very small, so they have a negligible effect on the expansion of the universe. Nevertheless, experimental efforts are underway to detect them (see Section 8.4.2).
2.3.3 Dark Energy
We have recently learned that matter and radiation aren't enough to describe the evolution of the universe. Instead the universe today to determined by a mysterious form of dark energy with negative pressure,𝛲 = -𝜌𝑐2 and hence constant energy density.
(2.110) 𝜌 ∝ 𝑎0
Since the energy density doesn't dilute, energy has to created on the universe expands. As described above, that doesn't violate the conservation of energy, as long as equation (2.106) is satisfied.
• Vacuum energy A natural candidate for a constant energy density is the energy associated to empty space itself.As the universe expands, more space is being created and this energy therefore increase in proportion to the volume. In quantum field theory, this so-called "vacuum energy" in actually predicted, leading to an energy-momentum tensor of the form
(2.111) 𝛵vac𝜇𝜈 = -𝜌vac𝑐2𝑔𝜇𝜈.
AS expected from Lorentz symmetry, the energy-momentum tensor associated to the vacuum to proportional to the spacetime metric. Comparison with (2.100) shows that this indeed gives 𝛲vac = -𝜌vac𝑐2. Unfortunately, as it will be described below, quantum field theory also predicts the size of the vacuum energy 𝜌vac to be much larger than the value inferred from cosmological observations.
• Cosmological constant The observation of dark energy has also revived the old concept of a "cosmological constant," originally introduced by Einstein to make the universe static. Note that the left-hand side of Einstein equation (2.94) isn't uniquely defined. We can add the term 𝛬𝑔𝜇𝜈 for some constant 𝛬, without changing the conservation of the energy-momentum tensor, ∇𝜇𝛵𝜇𝜈 = 0. To see this, you need to convince yourself that ∇𝜇𝑔𝜇𝜈 = 0. In other words, we could have written the Einstein equation as
(2.112) 𝐺𝜇𝜈 + 𝛬𝑔𝜇𝜈 = 8π𝐺/𝑐4 𝑇𝜇𝜈.
However it has been standard practice to move this extra terms to the right-hand side and treat it as a contribution to the energy-momentum tensor
(2.113) 𝛵(𝛬)𝜇𝜈 = 𝛬𝑐4/8π𝐺 𝑔𝜇𝜈 ≡ -𝜌𝛬𝑐2𝑔𝜇𝜈,
which is of the same form as (2.111).
• Dark energy The therm "dark energy" is often used to describe a more general fluid whose equation of state is not exactly that of a cosmological constant 𝜔 ≈ -1, or may even be varying in time. It is the failure of quantum field theory to explain the size of the observed vacuum energy that has led theorists to consider those more exotic possibilities. Whatever it is, dark energy plays a key role in the standard cosmological model-the 𝛬CDM model (see Section 2.4).
The cosmological constant problem*
When the cosmological constant was discovered, it came as a relief to observers, but was a shock to theorists. While it reconciled the age of the universe with the age of the oldest starts , its observed value is much smaller than all particle physics scales, making it hard to understand from a more fundamental perspective. This cosmological constant problem is the biggest crisis in modern theoretical physics.
In Section 2.4. we will see that the observed value of the vacuum energy is
(2.114) 𝜌𝛬𝑐2 ≈ 6 × 10-10 J m-3
To compare this to our expectation from particle physics, we had better to write it in units of high-energy physics, electron volts (eV). Using 1 J = 6.2 × 1018 eV and ħ𝑐 ≈ 2.0 × 10-7 eV m, we get (ħ𝑐)3𝜌𝛬𝑐2 = (10-3 eV)4. Written in natural units, with ħ = 𝑐 ≡ 1, we have then
(2.115) 𝜌𝛬 = (10-3 eV)4.
We see that the scale appearing in the vacuum energy, 𝑀𝛬 ∼ 10-3 eV, is much smaller than the typical scales relevant to particle physics.
Quantum field theory (QFT) predicts the existence of vacuum energy. However, the expected value of this vacuum energy is vastly too large. To start, recall that that in QFT every particle arises as an expectation of a fundamental field. Moreover, each field can be represented by an infinite number of Fourier modes with frequencies 𝜔𝜅. These Fourier modes satisfy the equation of a harmonic oscillator and therefore experience the same zero-point fluctuations as a quantum harmonic oscillator (see Section 8.2.1). In other words, the vacuum energy receive contributions of the form 1/2 ℏ𝜔𝜅 for each mode. The sum over all Fourier modes actually diverges. This divergence arises because we extrapolated our QFT beyond its regime of validity. Let us therefore assumed that our theory is valid only up to a cutoff scale 𝛭* and only contributions to the vacuum energy from modes with frequencies below the cutoff. The vacuum energy will now be finite, but depends on the arbitrary cutoff scale. The dependence on the cutoff can be removed by adding a counterterm in the form of a bare cosmological constant 𝛬0. After this process of renormalization, the remaining vacuum energy is
(2.116) 𝜌QFT ∼ 𝛴𝑖 𝑚4𝑖,
where the sum is over all particles with mass below the cutoff. In the absence of gravity this constant vacuum energy wouldn't affect any dynamics and is therefore usually discarded. The equivalence principle, however,implies that all forms of energy gravitate and hence affect the curvature of the spacetime. The vacuum energy is no exception.
The first to worry about the gravitational effects of zero-point energies was Wolfgang Pauli in the 1920s. Considering the contribution from the electron in (2.1116), he estimated that the induced curvature radius of the universe would be 106 km, so that "the world would not even reach to the moon". Including rest of the Standard Model only makes the problem worse:
(2.117) 𝜌QFT ≳ (1 TeV)4 = 1060 𝜌𝛬, [TeV = 1012 eV]
where we have added contributions up to the TeV scale. The enormous discrepancy between this estimate and the observed value in (2.114) is the cosmological constant problem.
But we can add an arbitrary constant to the QFT estimate to match the observed value of this vacuum energy
(2.118) 𝜌𝛬 = 𝜌QFT + 𝜌0.
To explain the small size of the observed vacuum energy would require two large numbers,𝜌QFT and 𝜌0 have 60 digits in common, but differ at the 61st digit, so that the sum of the two is smaller by 60 orders of magnitude. moreover, each time the universe goes through a phase transition, the value of 𝜌QFT changes, while the value of 𝜌0 presumably doesn't. For example, we expect the electroweakland QCD phase transition to induce jumps in the order of ∆𝜌QFT ∼ (200 GeV)4 and (0.3 GeV)4 respectively.Any tuning must explain the small value of the cosmological constant today and not at the beginning.
One way to explain the apparent fine-tuning to the vacuum energy is to appeal to the anthropic principle. Suppose that our universe is part of a much larger multiverse and that the fundamental physical parameters exhibit different values indifferent regions of space. In particular, imagine that the value of the vacuum energy varies across the multiverse. If the vacuum energy were much larger, dark energy would start to dominate before galaxies would have formed and complex structures could not have evolved. In other words, we shouldn't be shocked by the small value of the vacuum energy, since if it was any bigger w would not be around to ask the question. "We live where we can live" in a vast landscape of possibilities and the observed value of the cosmological constant is simply the accident of "environmental selection."
2.3.4 Spacetime Curvature
Having introduced the relevant types of matter and energy in the universe, we now want to see how they source the dynamic s of the spacetime. To do this, we have to compute the Einstein tensor on the left-hand side of the Einstein equation (2.84)
(2.119) 𝐺𝜇𝜈 = 𝑅𝜇𝜈 - 1/2 𝑅𝑔𝜇𝜈,
where 𝑅𝜇𝜈 is the Ricci tensor and 𝑅 = 𝑅𝜇𝜇 = 𝑔𝜇𝜈𝑅𝜇𝜈 is its trace, the Ricci scalar. In Appendix A, we give the following definition of the Ricci tensor
(2.120) 𝑅𝜇𝜈 ≡ ∂𝜆𝛤𝜆𝜇𝜈 - ∂𝜈𝛤𝜆𝜇𝜆 + 𝛤𝜆𝜆𝜌𝛤𝜌𝜇𝜈 - 𝛤𝜌𝜇𝜆𝛤𝜆𝜈𝜌.
Now we are going to compute (2.120) and (2.119) for the FRW spacetime. 𝑅𝑖0 = 𝑅0𝑖 = 0, because it is a 3-vector and therefore must vanish due to the isotropy of Robertson-Walker metric. The non- vanishing components of Ricci tensor are
(2.121) 𝑅00 = -3/𝑐2 (𝑑𝑎̇/𝑑𝑡)/𝑎,
(2.122) 𝑅𝑖𝑗 = 1/𝑐2 [(𝑑𝑎̇/𝑑𝑡)/𝑎 + 2 (𝑎̇/𝑎)2 + 2 𝑘𝑐2/𝑎2𝑅02] 𝑔𝑖𝑗.
Example Setting 𝜇 = 𝜈 = 0 in (2.120), we have
(2.123) 𝑅00 ≡ ∂𝜆𝛤𝜆00 - ∂0𝛤𝜆0𝜆 + 𝛤𝜆𝜆𝜌𝛤𝜌00 - 𝛤𝜌0𝜆𝛤𝜆0𝜌.
Since Christoffel symbols with two time indices-00- vanish, this reduces to
(2.124) 𝑅00 ≡ -∂0𝛤𝑖0𝑖 - 𝛤𝑖0𝑗𝛤𝑗0𝑖.
Using 𝛤𝑖0𝑗 = 𝑐-1(𝑎̇/𝑎)𝛿𝑖𝑗, {RE (2.45)] we find
(2.125) 𝑅00 = -1/𝑐2 𝑑/𝑑𝑡 (3 𝑎̇/𝑎) - 3/𝑐2 (𝑎̇/𝑎)2 = -3/𝑐2 (𝑑𝑎̇/𝑑𝑡)/𝑎. ▮
Example Computing 𝑅𝑖𝑗 can be greatly simplified using the following trick: we will compute 𝑅𝑖𝑗 at 𝐱 = 0 where the spatial metric is 𝛾𝑖𝑗 = 𝛿𝑖𝑗 and then argue that the result for general 𝐱 must have the form 𝑅𝑖𝑗 ∝ 𝑔𝑖𝑗. [RE (2.49) In FRW metric 𝑔𝑖𝑗 = 𝑎2𝛾𝑖𝑗]
In Cartesian coordinates the spatial metric is [RE (2.9-14)]
(2.126) 𝛾𝑖𝑗 = 𝛿𝑖𝑗 + 𝑘𝑥𝑖𝑥𝑗/[𝑅02 - 𝑘(𝑥𝑙𝑥𝑙)]. [Why? (𝐱 ⋅ 𝑑𝐱)2 = 𝑥𝑖𝑥𝑗; 𝐱2 = 𝑥𝑙𝑥𝑙]
The key point is to think ahead and anticipate that we will set 𝐱 = 0 at the end. In this condition the Christoffel symbols contain derivative metric and the Ricci tensor has another derivative, so there will be terms in the final answer with two derivatives acting on the metric from the second term. We only need to keep terms to quadratic order in 𝑥: [Why?]
(2.127) 𝛾𝑖𝑗 = 𝛿𝑖𝑗 + 𝑘𝑥𝑖𝑥𝑗/𝑅02 + 𝑂(𝑥4).
Plugging this into the definition of Christoffel symbol gives [RE (2.45) for Christoffel symbol in FRW metric]
(2.128) 𝛤𝑖𝑗𝑘 = 𝑘/𝑅02 𝑥𝑖𝛿𝑗𝑘 + 𝑂(𝑥3).
This vanishes at 𝐱 = 0, but the derivative does not. From the definition of Ricci tensor, we then have
(2.129) 𝑅𝑖𝑗(𝐱 = 0) ≡ (𝐴){∂𝜆𝛤𝜆𝑖𝑗 - ∂𝑗𝛤𝜆𝑖𝜆} + (𝐵){𝛤𝜆𝜆𝜌𝛤𝜌𝑖𝑗 - 𝛤𝜌𝑖𝜆𝛤𝜆𝑗𝜌}.
Let us start with (𝐵). Dropping terms that are zero at 𝐱 = 0, we find
(2.130) (𝐵) = 𝛤𝑙𝑙0𝛤0𝑖𝑗 - 𝛤0𝑖𝑙𝛤𝑙𝑗0 - 𝛤𝑙𝑖0𝛤0𝑗𝑙 = 3/𝑐2 𝑎̇/𝑎 𝑎𝑎̇𝛿𝑖𝑗 - 1/𝑐2 𝑎𝛿𝑖𝑙 𝑎̇/𝑎 𝑎𝛿𝑖𝑗 - 1/ 𝑐2 𝑎̇/𝑎 𝛿𝑙𝑖𝑎𝑎̇𝛿𝑗𝑙 = 𝑎̇2/𝑐2 𝛿𝑖𝑗.
The two terms labeled (𝐴) can be evaluated by using (2.128),
(2.131) (𝐴) = ∂0𝛤0𝑖𝑗 + ∂𝑡𝛤𝑙𝑖𝑗 - ∂𝑗𝛤𝑙𝑖𝑙 = 𝑐-2 ∂𝑡(𝑎𝑎̇)𝛿𝑖𝑗 + 𝑘/𝑅02 𝛿𝑙𝑖𝛿𝑖𝑗 - 𝑘/𝑅02 𝛿𝑙𝑗𝛿𝑖𝑙 = 𝑐-2 (𝑎𝑑𝑎̇/𝑑𝑡 + 𝑎̇2 + 2 𝑘𝑐2/𝑅02)𝛿𝑖𝑗.
Hence we get
(2.132) 𝑅𝑖𝑗(𝐱 = 0) = (𝐴) + (𝐵) = 1/𝑐2[𝑎𝑎̇ + 2𝑎̇2 + 2 𝑘𝑐2/𝑅02]𝛿𝑖𝑗 = 1/𝑐2[𝑎𝑑𝑎̇/𝑑𝑡 + 2𝑎̇2 + 2 𝑘𝑐2/𝑅02]𝛿𝑖𝑗 = 1/𝑐2[(𝑑𝑎̇/𝑑𝑡)/𝑎 + 2(𝑎̇/𝑎)2 + 2 𝑘𝑐2/𝑅02]𝑔𝑖𝑗(𝐱 = 0).
Since this is a relation between tensors, it holds for general 𝐱, so we get the result quoted in (2.122). ▮
Now we can calculate the Ricci scalar [𝑔𝜇𝜈 = diag(-1, 1/𝑎2 𝛾𝑖𝑗)
(2.133) 𝑅 = 𝑔𝜇𝜈𝑅𝜇𝜈 = -𝑅00 - 𝑔𝑖𝑗𝑅𝑖𝑗 = 3/𝑐2 (𝑑𝑎̇/𝑑𝑡)/𝑎 + 𝑔𝑖𝑗𝑔𝑖𝑗 1/𝑐2[(𝑑𝑎̇/𝑑𝑡)/𝑎 + 2(𝑎̇/𝑎)2 + 2 𝑘𝑐2/𝑅02] = 𝛿𝑖𝑖[(𝑑𝑎̇/𝑑𝑡)/𝑎 + 2(𝑎̇/𝑎)2 + 2 𝑘𝑐2/𝑅02] = 6/𝑐2 [(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑅02],
and the nonzero components of the Einstein tensor, 𝐺𝜇𝜈 ≡ 𝑔𝜇𝜆𝐺𝜆𝜈, are
(2.134) 𝐺00 = -3/𝑐2 [(ȧ/𝑎)2 + 𝑘𝑐2/𝑎2𝑅02],
Derivation From (2.119) 𝐺00 = 𝑔00𝐺00 = -𝐺00. -𝐺00= -𝑅00 + 1/2 𝑅𝑔00 = 3/𝑐2 (𝑑𝑎̇/𝑑𝑡)/𝑎 + 1/2 6/𝑐2 [(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑅02](-1) = -3/𝑐2 [(𝑎̇/𝑎)2 + 𝑘𝑐2/𝑎2𝑅02]. ▮
(2.135) 𝐺𝑖𝑗 = -1/𝑐2 [2(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑎2𝑅02]𝛿𝑖𝑗
Derivation 𝑔𝑖𝜆𝐺𝜆𝑗 = 𝐺𝑖𝑗. From (2.122) and (2.133) 𝐺𝑖𝑗 = 𝑅𝑖𝑗 -1/2 𝑅𝑔𝑖𝑗 = 1/𝑐2 [(𝑑𝑎̇/𝑑𝑡)/𝑎 + 2 (𝑎̇/𝑎)2 + 2 𝑘𝑐2/𝑎2𝑅02] 𝑔𝑖𝑗 - 1/2 6/𝑐2 [(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑅02]𝑔𝑖𝑗 = -1/𝑐2 [2(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑎2𝑅02] 𝑔𝑖𝑗, ⇒ 𝐺𝑖𝑗 = -1/𝑐2 [2(𝑑𝑎̇/𝑑𝑡)/𝑎 + (𝑎̇/𝑎)2 + 𝑘𝑐2/𝑎2𝑅02]𝛿𝑖𝑗. ▮
|
|
|





































