|
김관석
|
2024-09-18 13:58:05, 조회수 : 980 |
- Download #1 : BC_3c.jpg (179.2 KB), Download : 0

3.2 Beyond Equilibrium
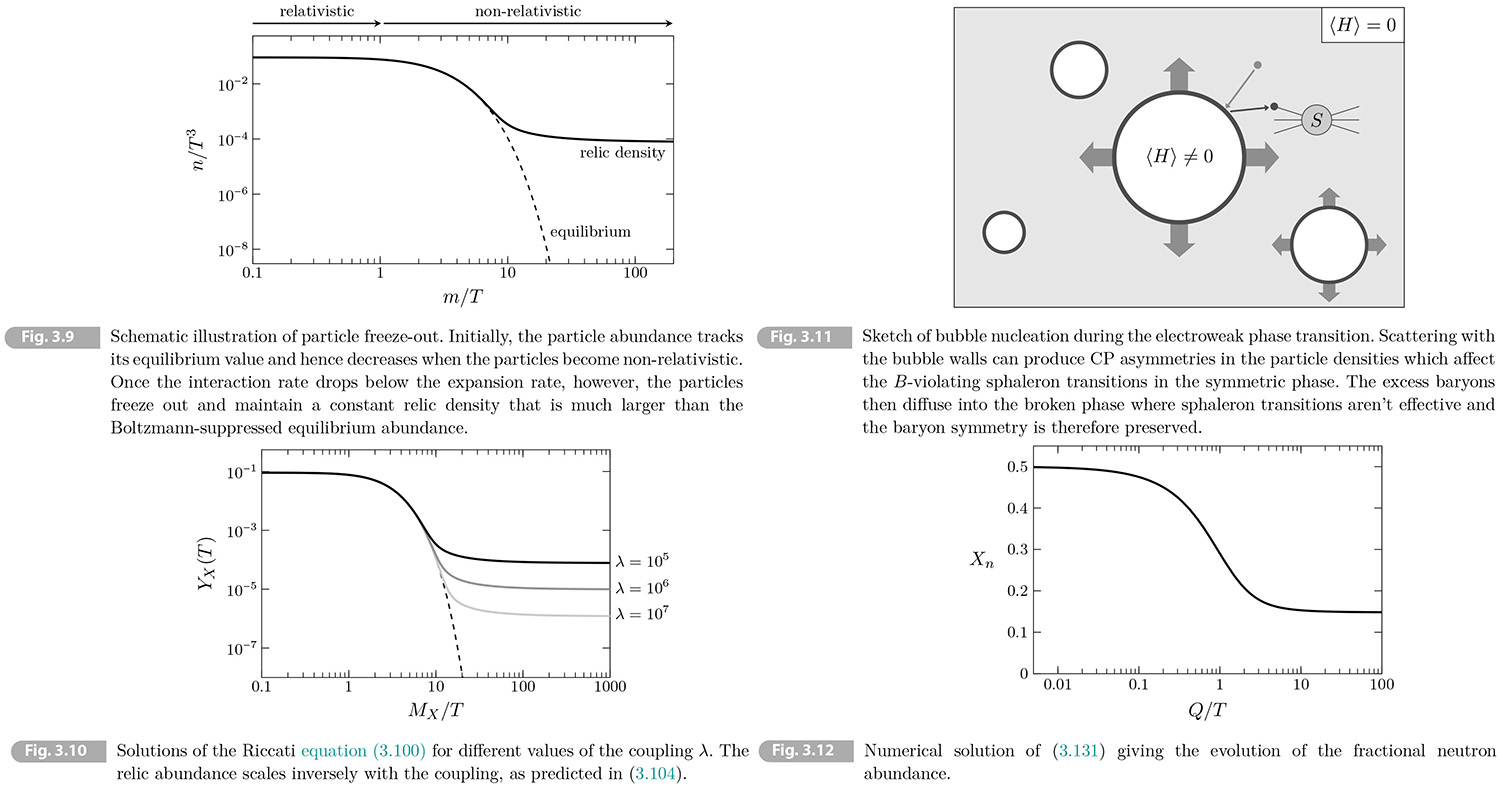
To understand the world around us, it is crucial to understand deviations from equilibrium. For example, a massive particle species in thermal equilibrium become exponentially rare when the temperature drops below the mass of particles, the numbers of particles in a comoving volume defined by the number density 𝑛𝑖 divided by the entropy density (3.52), 𝑁𝑖 ≡ 𝑛𝑖/𝑠 ~ (𝑚/𝛵)3/2 exp(-𝑚/𝛵). In order for these particles to survive until the present time, they must drop out of thermal equilibrium before 𝑚/𝛵 becomes much larger than unity. This decoupling, and the associated freeze-out of massive particles, occurs when the interaction rate of the particles becomes smaller the expansion rate (see Fig. 3.9).
The main tool to describe the evolution beyond equilibrium is the Boltzmann equation. In this section, the Boltzmann equation will be first introduced and then it will be applied to three important examples: (i) the production of dark matter; (ii) the formation of the light elements during Big Bang nucleosynthesis; and (iii) the freeze-out of electrons during recombination. Some comments about the role of non-equilibrium process in baryogenesis will also be made.
3.2.1 The Boltzmann Equation
In the absence of interaction, the number density of a particle species 𝑖 evolves as
(3.92) 𝑑𝑛𝑖/𝑑𝑡 + 3 𝑎̇/𝑎 𝑛𝑖 = 0,
which simply means that the number of particles in a fixed physical volume (𝑉 ∝𝑎3) is conserved, so that the density dilutes as 𝑛𝑖 ∝ 𝑎3. To include the effect of interactions, we add a collision term to the right-hand side of (3.92)
(3.93) 1/𝑎3 𝑑(𝑛𝑖𝑎3)/𝑑𝑡 = 𝐶𝑖[{𝑛𝑗}].
This is the Boltzmann equation.14 The form of the collision term depends on specific interaction. We will consider single-particle decays and two-particle scattering (or annihilations). Let us consider the following process
1 + 2 ⟷ 3 + 4,
where particle 1 interacts with particle 2 to produce particle 3 and 4, or the inverse can happen. Suppose we want to track the number density 𝑛1 of species 1. The Boltzmann equation simply formalizes this statement
(3.94) 1/𝑎3 𝑑(𝑛1,𝑎3)/𝑑𝑡 = -𝛼 𝑛1𝑛2 + 𝛽 𝑛3𝑛4.
We understand the right-hand side as follows: The first term, -𝛼𝑛1𝑛2 describes the distribution of particle 1, while the second term, +𝛽𝑛3𝑛4, account their production. The parameter 𝛼 = ⟨𝜎𝑣⟩, which denote an average over 𝑣, is the thermally-averaged cross section.15 The second parameter 𝛽 can be related to 𝛼 by noting that the collision term has to vanish in (chemical) equilibrium
(3.95) 𝛽 = (𝑛1𝑛2/𝑛3𝑛4)eq 𝛼,
where 𝑛𝑖eq are the equilibrium number densities that we calculated above. The relation in (3.95) is sometimes called detailed balance . We therefore find
(3.96) 1/𝑎3 𝑑(𝑛1𝑎3)/𝑑𝑡 = -⟨𝜎𝑣⟩ [𝑛1𝑛2 - (𝑛1𝑛2/𝑛3𝑛4)eq 𝑛3𝑛4].
It is instructive to write this in terms of the number of particles in a comoving volume, 𝑁𝑖 ≡ 𝑛𝑖/𝑠 ∝ 𝑛𝑖𝑎3. This gives
(3.97) 𝑑 ln 𝑁1/𝑑 ln 𝑎 = -𝛤1/𝐻 [1 - (𝑁1𝑁2/𝑁3𝑁4)eq 𝑁3𝑁4/𝑁1𝑁2],
where 𝛤1 ≡ 𝑛2⟨𝜎𝑣⟩ is the interaction rate of species 1. The right-hand side of (3.97) a factor describing the interaction efficiency,
𝛤1/𝐻, and a factor characterizing the deviation from equilibrium, [1 - ∙ ∙ ∙ ].
Derivation 𝐻 = 𝑎̇/𝑎 = 𝑑(ln 𝑎)/𝑑𝑡, 𝑛1𝑎3 ∝𝑁𝑖, so 1/𝑛1𝑎3 𝑑(𝑛1𝑎3)/𝑑𝑡 = 𝑑(ln 𝑁𝑖)/𝑑𝑡. By dividing the both side of (3.96) with 𝑛1𝑑(ln 𝑎)/𝑑𝑡[= 𝐻], Cancel 𝑑𝑡's at the left-hand side, and divide by 𝑛1𝑛2 in the bracket of right-hand side, then [𝑛1𝑛2/𝑛1𝑛2 - (𝑛1𝑛2/𝑛3𝑛4)eq 𝑛3𝑛4/𝑛1𝑛2] ⇒ 𝑛1𝑛2[1 - (𝑁1𝑁2/𝑁3𝑁4)eq 𝑁3𝑁4/𝑁1𝑁2], 𝛤1 ≡ 𝑛2⟨𝜎𝑣⟩, we therefore get (3.97). ▮
When the interaction rate is large, 𝛤1 ≫ 𝐻, the natural state of the system is to be equilibrium. Imagine that 𝑁1 ≫ 𝑁1eq, while 𝑁𝑖 ~ 𝑁𝑖 eq , 𝑖 = 2, 3, 4. The right-hand side then is negative, particles of type 1 are destroyed and 𝑁1 is reduced towards the equilibrium value 𝑁1eq. similarly, if 𝑁1 ≪ 𝑁1eq, the right-hand side of (3.97) is positive and 𝑁1 is driven towards 𝑁1eq. The same condition applies if several species deviate from their equilibrium values. As long as the interaction rates are large, the system therefore quickly relaxes to a steady state where the source in (3.97) vanishes and the particles assume their equilibrium abundances. At some point, however, the reaction rate drops below the Hubble scale, 𝛤1 < 𝐻. The right-hand side of (3.97) then gets suppressed and the comoving density of particles approaches a constant relic density, 𝑁1 → const.
3.2.2 Dark Matter Freeze-out
We will begin with a simple application of the Boltzmann equation (3.96): the freeze-out of massive particles. This may be how dark matter was produced in the early universe.
Decoupling and freeze-out
Consider a heavy fermion 𝑋 that can annihilate with its antiparticle 𝑋̄ to produce two light (essentially massless) particles,
𝑋 + 𝑋̄ ⟷ 𝓁 + 𝓁̄.
The particle 𝑋 might be the dark matter, while 𝓁 could be particles of the Standard Model.
We will make a few simplifying assumptions: First, we will take the light particle 𝓁 to be tightly coupled to the rest of the plasma, as would be the case, for instance, if the particles were electrically charged. The light particles will then maintain their equilibrium densities throughout, 𝑛𝓁 = 𝑛𝓁eq. Second, we will neglect any initial asymmetry between 𝑋 and its antiparticle 𝑋̄, so that 𝑛𝑋 = 𝑛𝑋̄, Finally we will assume that there are no other particle annihilations during the freeze-out of the species 𝑋. This will allow us to take 𝛵 ∝ 𝑎-1 for the times relevant to the freeze-out.
With these assumptions, the Boltzmann equation (3.96) for the evolution of the particle 𝑋 becomes
(3.98) 1/𝑎3 𝑑(𝑛𝑋,𝑎3)/𝑑𝑡 = -⟨𝜎𝑣⟩ [𝑛𝑋2- (𝑛𝑋eq)2]
Now we introduce the quantity 𝑌𝑋 ≡ 𝑛𝑋/𝛵3, which is proportional t the number of particles in a comoving volume, 𝑁𝑋 ≡ 𝑛𝑋/𝑠 ∝ 𝑌𝑋. In fact, as long as 𝛵 ∝ 𝑎-1, we can treat 𝑌𝑋 and 𝑁𝑋 interchangeably. In terms of 𝑌𝑋, the left-hand side of (3.98) becomes 𝛵3𝑑𝑌𝑋/𝑑𝑡. Since most of the interesting dynamics will take place when 𝛵 ~ 𝑀𝑋, a new measure of time will be defined,
(3.99) 𝑥 ≡ 𝑀𝑋/𝛵, where 𝑑𝑥/𝑑𝑡 = 𝐻𝑥.
For weakly interacting particles, the decoupling occurs at very early times, during the radiation-dominated ear, where the Hubble parameter can be written as 𝐻 = 𝐻(𝑀𝑋)/𝑥2.[verification. needed] [RE Dodelson p.74] Equation (3.98) then becomes the so-called Riccati equation,
(3.100) 𝑑𝑌𝑋/𝑑𝑡 = 𝜆/𝑥2 [𝑌𝑋2 - (𝑌𝑋eq)2],
where we have defined the dimensionless parameter
(3.101) 𝜆 ≡ 𝛤(𝑀𝑋)/𝐻(𝑀𝑋) = 𝑀𝑋3⟨𝜎𝑣⟩/𝐻(𝑀𝑋).
For simplicity, we will take 𝜆 to be a constant. Although there are no analytical solutions to (3.100), we can solve the Riccati equation numerically using the equilibrium abundance as an initial condition.
Fig. 3.10 shows numerical solutions of (3.100) for different values of 𝜆. As expected, at high temperatures 𝑥 ≪ 1, we have 𝑌𝑋 ≈ 𝑌𝑋eq = 3𝜁(3)/4π2 ≈ 0.1, while at low temperature, 𝑥 ≫ 1, the equilibrium abundance exponentially suppressed, 𝑌𝑋eq ~ (𝑥/2π)3/2𝑒-𝑥. Eventually, the massive particles will become so rare that they will not be able to find each other fast enough to maintain the equilibrium abundance. We see that this freeze-out happens at about 𝑥𝑓 ~ 10.
The final relic abundance, 𝑌𝑋∞ ≡ 𝑌𝑋(𝑥 = ∞), determines the freeze-out density of the massive particles. Let us estimate its magnitude as a function of the interaction strength 𝜆. Well after freeze-out, 𝑌𝑋 will much larger than 𝑌𝑋eq. Thus, at late time, we can drop 𝑌𝑋eq from Boltzmann equation, so that
(3.102) 𝑑𝑌𝑋/𝑑𝑥 ≈ 𝜆𝑌𝑋2/𝑥2.
Integrating this from 𝑥 = 𝑥𝑓 to 𝑥 = ∞, we find [𝑑𝑌/𝑑𝑥 = 𝜆𝑌2/𝑥2, 𝑑𝑌/𝑌2 = 𝜆𝑑𝑥/𝑥2 ⇒ -1/𝑌 = 𝜆/𝑥.]
(3.103) 1/𝑌𝑋∞ - 1/𝑌𝑋𝑓 = 𝜆/𝑥𝑓,
where 𝑌𝑋𝑓 ≡ 𝑌𝑋(𝑥𝑓). Typically 𝑌𝑋𝑓 ≫ 𝑌𝑋∞, so a simple analytic approximation for relic abundance is
(3.104) 𝑌𝑋∞ ≈ 𝑥𝑓/𝜆.
We have seen that a good order-of-magnitude estimate is 𝑥𝑓 ~ 10. Using this value, the estimate in (3.104) in excellent agreement with the numerical results in Fig. 3.10. Moreover, 𝑥𝑓 value isn't terribly sensitive to 𝜆 value, since 𝑥𝑓(𝜆) ∝ ∣ln 𝜆∣, where the logarithmic scaling can be understood from the decoupling condition 𝛤(𝑥𝑓) ≈ 𝐻(𝑥𝑓). [verification. needed]
Equation (3.104) predicts that the freeze-out abundance 𝑌𝑋∞ decrease as the interaction rate 𝜆 increases. This makes intuitive senses: larger interaction maintain equilibrium for a longer time, deeper into the Boltzmann-suppressed regime. Since the estimate in (3.104) works very well, we will use following.
Dark matter density
We would like to relate the freeze-out abundance of the dark matter relics to their density today. To do this we note that the number density of the particle after freeze-out decreases as 𝑛𝑋 ∝ 𝑎-3. We can then write the number density today as
(3.105) 𝑛𝑋,0 = 𝑛𝑋,1 (𝑎1/𝑎0)3 = 𝑌𝑋∞𝛵03 (𝑎1𝛵1/𝑎0𝛵0)3. [𝑌𝑋 ≡ 𝑛𝑋/𝛵3; 𝑛𝑋,1 (𝑎1/𝑎0)3 = 𝑌𝑋∞𝛵13 (𝑎1/𝑎0)3]
where 𝑎1 is an arbitrary time that is late enough for species to have reached their relic abundance, but before any additional particle annihilations have become relevant. As we have seen, such particle annihilation lead to deviations from the scaling 𝛵 ∝𝑎-1, so that the final factor in (3.105) isn't simply unity. Using the conservation of entropy (3.54), 𝑔*𝑆(𝑎𝛵)3 = const. we instead get
(3.106) 𝑛𝑋,0 = 𝑌𝑋∞𝛵03 𝑔*𝑆(𝛵0)/𝑔*𝑆(𝑀𝑋) without momentum, 𝑝.
The normalized energy density of the particles then is, using (3.2) 𝐻2 = 𝜌/3𝑀𝑃𝑙2, 𝐸 = 𝑀𝑋 without momentum, 𝑝, (3.104) and (3.101),
(3.107) 𝛺𝑋 = 𝜌𝑋,0/𝜌crit,0 = 𝑀𝑋𝛵03/3𝑀𝑃𝑙2𝐻02 = 𝑀𝑋𝑛𝑋,0/3𝑀𝑃𝑙2𝐻02 𝑥𝑓/𝜆 𝑔*𝑆(𝛵0)/𝑔*𝑆(𝑀𝑋) = 𝐻(𝑀𝑋)/𝑀𝑋2 𝛵03/3𝑀𝑃𝑙2𝐻02 𝑥𝑓/⟨𝜎𝑣⟩ 𝑔*𝑆(𝛵0)/𝑔*𝑆(𝑀𝑋),
Using (3.55), 𝐻2 ≈ π2/90 𝑔* 𝛵/𝑀𝑃𝑙2, for 𝐻(𝑀𝑋), this becomes
(3.108) 𝛺𝑋 ≈ π/√90 𝛵03/3𝑀𝑃𝑙2𝐻02 𝑥𝑓/⟨𝜎𝑣⟩ √[𝑔*(𝑀𝑋)] 𝑔*𝑆(𝛵0)/𝑔*𝑆(𝑀𝑋).
Finally, we use 𝑔*𝑆(𝑀𝑋) = 𝑔*(𝑀𝑋) considering (3.51) and insert the measured value of 𝛵0 and 𝐻0 as well as 𝑔*𝑆(𝛵0) = 3.91, to get
(3.109) 𝛺𝑋 ~ 0.1 𝑥𝑓/√[𝑔*(𝑀𝑋)] 10-8 GeV-2/⟨𝜎𝑣⟩
This result is insensitive to the mass of the new particles and is mostly determined by their cross section. The observed dark matter density is reproduced if
√⟨𝜎𝑣⟩ ~ 10-4 GeV-1 ~ 0.1 √G𝐹. [RE Wikipedia Fermi's interaction: Fermi constant, GF ≈ 1.16×10−5 GeV-2]
The fact that a thermal relic with a cross section characteristic of the weak interaction gives the right order of magnitude for the dark matter abundance today is called the WIMP miracle.16
3.2.3 Baryogenesis: A Sketch*
The same analysis can also be applied to annihilation of baryons 𝑏 + 𝑏̄ ⟷ 𝛾 + 𝛾. Since the effective interaction between nucleons is mediated by pions, we can estimate the annihilation cross section as ⟨𝜎𝑣⟩ ~ 1/𝑚π2, with 𝑚π ≈ 140 MeV, Substituting this into (3.109), we then find
(3.110) 𝛺𝑏 ≈ 10-11,
which is much smaller than the observed value. This illustrates the need for baryogenesis to produce the abundance of baryons in the early universe. A lazy option would be to simply impose the baryon asymmetry as an initial condition. Much more satisfying would be to start with a baryon-symmetric universe and hen see the asymmetry between matter and antimatter arise dynamically.
Sakharov conditions
In 1967, Sakharov identified three necessary conditions that any successful theory of baryogenesis must satisfy. These Sakharov conditions are:
1. Violation of baryon number. The interactions that generate the baryon asymmetry must violate baryon number symmetry. It should be rather obvious that a universe with vanishing baryon number, 𝛣 = 0, can only evolve into a universe with 𝛣 ≠ 0 if the interactions don't conserve the baron number.
In the Standard Model (SM), baryon number is an "accidental symmetry," meaning that all renormalizable interactions have this symmetry because of the gauge symmetry of the SM. Despite baryon number being a symmetry of SM Lagrangian, baryon number violation occurs at the quantum level through the so-call "triangle anomaly". Nonperturbatively, this can lead "sphaleron transitions" which convert baryons to antilepton and thus change the baryon number.17 Theories beyond the SM-such as Grand Unified Theories (GUTs)- may violate baryon number even in the Lagrangian (i.e. at tree level).
2. Violation of C and CP. Slightly less obvious is that the interactions must violate C (charge conjugation) and CP (charge conjugation combined with parity). If C was an exact symmetry, then the probability of the process 𝑖 → 𝑗 would be equal to the corresponding antiparticles, 𝑖̄ → 𝑗̄, and no net baryon number would be generated. To see why CP must be violated, we first note that CPT (with T being time reversal) is a symmetry in any relativistic quantum field theory. CP invariance is therefore equivalent to invariance under time reversal. Consider the process 𝑖(𝐩a,𝐬a) → 𝑓(𝐩a,𝐬a), where 𝐩a are momenta of the particles and 𝐬a are their spins. Under time reversal, this becomes 𝑓(-𝐩a,-𝐬a) → 𝑖(-𝐩a,-𝐬a). If the time reversal is unbroken, then integrating over all momenta and summing over all spins would lead to vanishing net baryon number.
Both C and CP are violated by the weak interaction. The SM therefore, in principle, contains the required symmetry breaking, but whether is the breaking is strong enough to explain the size of the baryon asymmetry in our universe remains to be seen.
3. Departure from equilibrium. Finally, the process that generate the baryon asymmetry must occur out of thermal equilibrium. For non-relativistic particles and antiparticles in equilibrium, we have
(3.111) 𝛣 ∝ 𝑛𝑋 - 𝑛𝑋̄ = 2𝑔𝑋(𝑀𝑋𝛵)3/2 𝑒-𝑀𝑋/𝛵 sinh(𝜇𝑋/𝛵),
where 𝜇𝑋 is the chemical potential. By the first Sakharov condition, 𝑋 and 𝑋̄ undergo 𝛣-violating reactions, such as
𝑋 𝑋 → 𝑋̄ 𝑋̄.
If these reactions occur in equilibrium, then 𝜇𝑋 = 0 and 𝛣 = 0 in (3.111). The necessary out-of-equilibrium conditions can be provided by the cosmological evolution, making baryogenesis an interesting interplay between cosmology and particle physics.
Out-of-equilibrium decay
A simple toy model for baryogenesis will be sketched: the out-of-equilibrium decay a massive particle. The decay rate of particles is 𝛤𝑋, and most of the decay occurs when the age of the universe is of the order of the particles's lifetime, 𝑡 ~ 𝐻-1 ~ 𝛤𝑋-1. If the decay violates baron number, then a baryon asymmetry will be generated.
For concreteness, we assume that the 𝑋 particle has two decay channels 𝑎 and 𝑏, with baryon numbers 𝛣𝑎 and 𝛣𝑏. Similarly, the antiparticle 𝑋̄ has the decay channels 𝑎̄ and 𝑏̄ with baryon numbers -𝛣𝑎 and -𝛣𝑏. The branching ratios for the decay are
(3.112) 𝑟 ≡ 𝛤(𝑋 → 𝑎)/𝛤𝑋, 𝑟̄ = 𝛤(𝑋̄ → 𝑎̄)/𝛤𝑋, 1 - 𝑟 ≡ 𝛤(𝑋 → 𝑏)/𝛤𝑋, 1 - 𝑟̄ = 𝛤(𝑋̄ → 𝑏̄)/𝛤𝑋,
where we have used that the total decay rates of 𝑋 and 𝑋̄ are equal (because of CPT symmetry and unitarity). The net baryon number produced in the decays of 𝑋 and 𝑋̄ then is
(3.113) ∆𝛣 ≡ 𝛣𝑋 + 𝛣𝑋̄ = [𝑟𝛣𝑎 + (1 - 𝑟)𝛣𝑏] + [1 - 𝑟̄𝛣𝑎 - (1 - 𝑟̄)𝛣𝑏] = (𝑟 - 𝑟̄)(𝛣𝑎 - 𝛣𝑏).
If the baryon number isn't violated in the individual decays, then 𝛣𝑎 = 𝛣𝑏 = 0 and hence ∆𝛣 = 0. Similarly, if C and CP are preserved, then 𝑟 = 𝑟̄ and ∆𝛣 = 0. This illustrates the necessity of Sakharov conditions for baryogenesis.
The net baryon number density produced by the decays is 𝑛𝛣 = ∆𝛣 𝑛𝑋. Using that 𝑛𝑋 ~ 𝑛𝛾 at the time of the decay, we get
(3.114) 𝜂 = 𝑛𝛣/𝑛𝛾 ~ ∆𝛣,
which relates the cosmologically observed baryon-to-photon ratio to the amount of baryon number violation. Hence, we have assumed that the entropy release in the decays is negligible, which is not always a good approximation. Finally, a more accurate computation would also involve explicit integration of the Boltzmann equation.
Models of baryogenesis
There are many other scenarios. Some popular models of baryogenesis will be described very briefly. Refer to the suggested reference for more detail.
• Gut baryogenesis Grand Unified Theories unifying the strong and weak interactions generally contain baryon number-violating interactions. In the effective theory of the Standard Model, these interaction appear as higher-dimensional operators suppressed by a large scale and are often constrained by a the absence of proton decay. The baryon asymmetry then be created by the out-of-equilibrium decay of a heavy particle, as sketched above. The non-observation of proton decay puts a lower bound on the mass of the decaying particle, which can be in tension with the reheating temperature after inflation.
(Refer to some papers [12-18] for more detail.)
• Electroweak baryogenesis Within the SM, at first sight, all the Sakharnov conditions could be satisfied: (i) sphalerons provide baryon number violation, (ii) weak interactions (EW) violate C and CP, and (iii) the electroweak phase transition provide out-of-equilibrium conditions. However, on closer inspection, The EW phase transition is not strongly first order (as required because sphaleron transition would wash out the baryon asymmetry in a second-order phase transition) and the size of the CP violation is too small. Therefore new physics is required to change the nature of the EW phase transition and provide new sources of CP violation. Nevertheless, it remains an attractive option. (Refer to reviews [11, 26-28].
During a first-order phase transition, bubbles of the broken phase (with nonzero Higgs vacuum expectation value, ⟨𝐻⟩ ≠ 0) nucleate within the surrounding plasma in the unbroken phase (with ⟨𝐻⟩ = 0); see Fig. 3.11. These bubbles expand and coalesce until only the broken phase remains. If the underlying theory contain CP violation, then the scattering of particles with the bubble walls can generate CP asymmetries in the particle number densities. These asymmetries diffuse into the symmetric phase leading to a biasing of electroweak sphaleron transitions which producing a net baryon symmetry. Some of the excess baryons are then transferred to the broken phase where the rate of sphaleron transition transitions is strongly suppressed, so that the baryon asymmetry is preserved.
• Leptogenesis Another interesting possibility is to generate via leptogenesis.{29] Imagine a theory beyond the SM with an extra heavy (but sterile) neutrino (like in the "seesaw mechanism" for neutrino masses). If the decay of this heavy neutrino violates CP, then it could produce more antileptons than leptons. These antileptons are then transformed into baryon by sphaleron transitions. The end result is an excess of baryons over antibaryons.18
3.2.4 Big Bang Nucleogenesis
As our next example, we will use the Boltzmann equation to follow the evolution of baryonic matter in the early universe. since baryon number is conserved, the total number of nucleons stays constant. However, weak nuclear reactions convert neutrons and protons into each other and strong nuclear reactions will build heavier nuclei from them. In this section, how the light elements-hydrogen, helium and lithium-were synthesized in the Big Bang will be shown. But all of the complicated detail of BBN won't be given.19 Instead our goal is a theoretical understanding of a single number, the ratio of the (mass) density of helium to hydrogen, This number is one of the key predictions of the Big Bang theory.
(3.115) 𝑌𝑃 ≡ 𝑛4𝐻𝑒/𝑛𝐻 ~ 1/4. *[Correction: 4𝑛𝐻𝑒 → 𝑛4𝐻𝑒]
Let us briefly sketch the main sequence of events during BBN. At early times, the baryonic matter was mostly in the form of protons and neutrons, which were coupled to each other by 𝛽-decay and inverse 𝛽-decay:
(3.116) 𝑛 + 𝜈𝑒 ⟷ 𝑝+ + 𝑒-, 𝑛 + 𝑒+ ⟷ 𝑝+ + 𝜈̄𝑒,
where 𝜈𝑒 and 𝜈̄𝑒 are electron neutrinos and antineytrinos. Initially, the relative abundance of the protons and neutrons were determined by equilibrium thermodynamics. Around 1 MeeV the reaction in (3.116) became inefficient and the neutrinos decoupled. We will determine the freeze-out abundance by solving the relevant Boltzmann equation. Free neutrons decay until neutrons and protons combined into deuterium20
(3.117) 𝑛 + 𝑝+ ⟷ 𝐷 + 𝛾.
This occurred at a temperature around 0.1 MeV. Finally, the deuterium nuclei fused into helium
(3.118) 𝐷 + 𝑝+ ⟷ 3𝐻 + 𝛾. 𝐷 + 3𝐻 ⟷ 4𝐻 + 𝑝+.
In this way, essentially all of the primordial neutrons got converted into helium. The formation of heavier elements was very inefficient, which is why most protons survived and became the hydrogen in the universe.
Equilibrium
About 𝛵 ≈ 0.1 MeV, only free protons and neutrons existed, while other light nuclei hadn't been formed yet. We can therefore first solve for the neutron-to-proton ratio and the use this abundance as an input for the synthesis of deuterium, helium, etc.
Consider the reactions in (3.116). Let us assume that the chemical potentials of the electrons and neutrinos are negligibly small, so that 𝜇𝑛 = 𝜇𝑝. Using (3.71) for the equilibrium number densities 𝑛𝑖eq, we then have
(3.119) (𝑛𝑛/𝑛𝑝)eq = (𝑚𝑛/𝑚𝑝)3/2 𝑒-(𝑚𝑛 - 𝑚𝑝)/𝛵.
The small difference between the proton and neutron masses can be ignored in the prefactor, but has to be kept in the exponential. Hence, we find
(3.120) (𝑛𝑛/𝑛𝑝)eq = 𝑒-𝑄/𝛵,
where 𝑄 ≡ 𝑚𝑛 - 𝑚𝑝 = 1.30 MeV. For 𝛵 ≫ 1 MeV, there are as many neutron as protons, while 𝛵 < 1 MeV, the neutron fraction gets smaller. If the weak interactions would operate efficiently enough to maintain equilibrium indefinitely, then the neutron abundance would drop to zero. But in the real world , the weak interactions are not so efficient.
Neutron freeze-out
Since essentially all the neutrons eventually become incorporated into 4𝐻, the primordial ratio of neutrons protons is particularly important. For convenience we define
(3.121) 𝑋𝑛 ≡ 𝑛𝑛/(𝑛𝑛 + 𝑛𝑝),
and, using (3.120), we get
(3.122) 𝑋𝑛eq(𝛵) = 𝑒-𝑄/𝛵/(1 + 𝑒-𝑄/𝛵).
follow this equilibrium abundance until weak interaction processes such as (3.116) effectively shut off around 𝛵 ~ 1MeV (roughly at the same time as neutrino decoupling).21 To follow this evolution in detail, we must solve the Boltzmann equation (3.96), with 1 = neutron, 3 = proton, and 2, 4 = leptons (𝑛𝓁 = 𝑛𝓁eq):
(3.123) 1/𝑎3 𝑑(𝑛𝑛𝑎3)/𝑑𝑡 = -𝛤𝑛 [𝑛𝑛 - (𝑛𝑛/𝑛𝑝)eq𝑛𝑝],
where 𝛤𝑛 = 𝑛𝓁⟨𝜎𝑣⟩ is the rate for neutron /proton conversion. Substituting (3.121) and (3.122) into (3.123), we find
(3.124) 𝑑𝑋𝑛/𝑑𝑡 = -𝛤𝑛 [𝑋𝑛 - (1 - 𝑋𝑛) 𝑒-𝑄/𝛵]. [Dodelson p.66, the total density (𝑛𝑛 + 𝑛𝑝) times 𝑎3 (is preserved and) can be taken outside the derivative]
The key input from article physics is the rate 𝛤𝑛. We have from (3.116)
(3.125) 𝛤𝑛 = 𝑛𝜈⟨𝜎(𝑛𝑣𝑒 → 𝑝+𝑒-)𝑣⟩ + 𝑛𝑒⟨𝜎(𝑛𝑒+ → 𝑝+𝜈̄𝑒)𝑣⟩,
where the neutrino and positron densities are
(3.126) 𝑛𝑒 = 2𝑛𝜈 = 3𝜁(3)/2π2 𝛵3.
Moreover, the relevant thermally-averaged cross sections are [Dodelson p.67]
(3.127) ⟨𝜎(𝑛𝑣𝑒 → 𝑝+𝑒-)𝑣⟩ = 510π2/{3𝜁(3) 𝜏𝑛} (12𝛵 + 6𝑄𝛵 + 𝑄2)/𝑄3, ⟨𝜎(𝑛𝑒+ → 𝑝+𝜈̄𝑒)𝑣⟩ = 255π2/{3𝜁(3) 𝜏𝑛} (12𝛵 + 6𝑄𝛵 + 𝑄2)/𝑄3,
where 𝜏𝑛 = 886.7±0.8 s is the neutron lifetime. The total neutron/proton conversion rate then is
(3.128) 𝛤𝑛(𝑥) = 255/𝜏𝑛 (12 + 3𝑥 + 𝑥2)/𝑥5,
where 𝑥 ≡ 𝑄/𝛵,
(3.129) 𝐻(𝑥) = √(𝜌/3𝑀𝑝𝑙2) = π/3 √(𝑔*/10) 𝑄2/𝑀𝑝𝑙 1/𝑥2
where 𝑔* = 10.75 and 𝐻 = 1.13 s-1. [Dodelson pp.66-67. 𝐻 = √(8π𝐺𝜌)/3, 𝜌 = π2/30 𝛵2 [𝛴𝑖=bosons 𝑔𝑖 + 7/8 𝛴𝑖=fermions 𝑔𝑖] (𝑖 relativistic) ≡ 𝑔* π2/30 𝛵2, 𝑔* = 2(𝑔𝛾) + 7/8[6(𝑔𝜈 + 2(𝑔𝑒) + 2(𝑔𝑝) ≃ 10.75, 𝐻(𝑥 = 1) = √(4π3𝐺𝑄4/45) × √10.75 = 1.13 sec-1.] This shows s that the conversion time 𝛤𝑛-1 = 0.60 is comparable to the age of the universe 𝑡 = (2𝐻)-1 = 0.74 s. [RE (3.55-56)] Since 𝛤𝑛-1 ∝ 𝛵-3 ∝ 𝑡3/2, the interaction time eventually becomes longer than the age of the universe and the neutron- to-proton ration approaches a constant. [verification. needed]
We can solve the Boltzmann equation (3.124) numerically. It is useful to choose an evolution variable that focuses on the dynamics at 𝛵 ~ 𝑄. Using 𝑥 = 𝑄/𝛵, [i.e. 𝑥 =1], we can the left-hand side of (3.124) as
(3.130) 𝑑𝑋𝑛/𝑑𝑡 = 𝑑𝑥/𝑑𝑡 𝑑𝑋𝑛/𝑑𝑥 = -𝑥/𝛵 𝑑𝛵/𝑑𝑡 𝑑𝑋𝑛/𝑑𝑥 = 𝑥𝐻 𝑑𝑋𝑛/𝑑𝑥,
where we have 𝛵 ∝𝑎-1 in the last equality. [Since 𝛵 ∝𝑎-1 from (3.54), 𝛵 ∝ 𝑔*𝑆-1/3𝑎-1, then we have -1/𝛵 𝑑𝛵/𝑑𝑡 = 𝐻.] So we get
(3.131) 𝑑𝑋𝑛/𝑑𝑥 = 𝛤𝑛(𝑥)/𝐻(𝑥 = 1) 𝑥[𝑒-𝑥 - 𝑋𝑛(1 + 𝑒-𝑥)].
The numerical solution of this equation is shown in Fig. 3.12. We see that the freeze-out of neutron abundance is
(3.132) 𝑋𝑛∞ ≡ 𝑋𝑛(𝑥 = ∞) = 0.15.
A rough estimate of the freeze-out abundance can also be obtained by evaluating the equilibrium abundance (3.122) at the time of neutrino decoupling, 𝛵𝑓 ~ 0.8 MeV, which gives 𝑋𝑛∞ ~ 1/6.
Neutron Decay
At temperature below 0.2 MeV (or 𝑡 ≳ 100 s) the finite lifetime of neutron becomes important. To include this neutron decay in our computation, we simply multiply the freeze-out abundance (3.132) by an exponential decay factor
(3.133) 𝑋𝑛(𝑡) = 𝑋𝑛∞ 𝑒-𝑡/𝜏𝑛 ≈ 0.15 𝑒-𝑡/887 s.
It is now a race against time. If the onset of nucleosynthesis takes significantly longer than the neutron lifetime, than the number of neutrons becomes exponentially small and not much fusion will occur. Fortunately, this is not the case in our universe.
14 Strictly speaking, it's the "integrated Boltzmann equation." A more fundamental Boltzmann equation for the evolution of the distribution function 𝑓𝑖 will be introduced in Appendix B.
15 Cross sections are the fundamental observables in particle physics. They describes the probability of a certain scattering process. We will simply use dimensional analysis to estimate the few cross sections. They may depend on the relative velocity 𝑣 of particles 1 and 2.
16 WIMP stands for weakly interacting massive particle. WIMPs used to be a very popular dark matter candidate because of the result in (3.109). However, recent direct detection experiments have put pressure on the WIMP scenario. Alternative dark matter candidate, such as non-thermal axions have increase in popularity.
17 Sphalerons are nonpertubative solution of the elctroweak field equation, corresponding to the collective excitation of 𝑊, 𝑍 and Higgs fields. They rather spectacular objects. The typical size of a sphaleron is 10-17 m, so that its volume is a 1000 000 times smaller than that of proton, while the mass is around 10 TeV, or 10 000 times the mass of a proton. Sphalerons are therfore 10 billion times denser than proton.
18 Interest in leptogenesis was recently revived by hints of confirmed CP violation for the ordinary neutrinos by the T2K experiment [Ref. 3-30]. If confirmed, this would make a plausible that CP violation also play an imortant role for sterile neutrinos (if they exist).
19 The detailed predictions of BBN can be computed numerically using the code PRIMAT. Thanks to Cyril Pitrou for making the code open to public.
20 The reaction is very similar to the reaction 𝑒- + 𝑝+ → 𝐻 + 𝛾 in Section 3.1.5. Our analysis will therefore be virtually identical to the Saha analysis of recombination.
21 It is fortunate that 𝛵𝑓 ~ 𝑄. This seams to be a coincidence: 𝑄 is determined by the strong and electromagnetic interaction, while 𝛵𝑓 is by the weak interaction. Imagine a 𝛵𝑓 ≪ 𝑄.
|
|
|





































