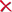|
김관석
|
2020-12-30 10:08:07, 조회수 : 687 |
- Download #1 : MA_Fig_3.jpg (342.3 KB), Download : 9

2 Gravity
2.1 Newton's Law of Gravity
The equation for Newton's Law of gravity is
𝐹𝑔 = 𝐺 𝑚1𝑚2/𝑅2,
where 𝐺, the universal gravitational constant has the same value throughout the known universe, and the value in SI units is 6.67 ⨯ 10-11 N m2/kg2. 𝑅 represents the distance between the center of mass 1 and the center of mass 2.
For example the force of gravity of the Earth on a person who weighs 100 kilograms standing on the Earth's surface is
(2.1) 𝐹𝑔 = (6.67 ⨯ 10-11 N m2/kg2)[(100 kg)(6 ⨯ 1024 kg)/(6.378 ⨯ 106 m)2] = 983.8 N. (𝑅Earth = 6378 km and 𝑚Earth = 6 ⨯ 1024 kg)
2.2 Newton's Law of Motion
First Law An object at rest will remain at rest unless an unbalanced force acts upon it, and an object in motion will continue moving at the same speed and in the same direction unless an unbalanced force acts upon it. The First Law is sometimes called "the law of inertia" which means resistance to acceleration.
Second Law If an unbalanced force (𝐹) acts upon an object of mass (𝑚), the object will experience an acceleration (𝑎) given by
(2.3) 𝑎 = 𝐹/𝑚 or 𝐹 = 𝑚𝑎.
To find the acceleration of anobject near the surface of the Earth, just plug the value foe the Earth's mass and radius.
(2.4) 𝑎 = 𝐹𝑔/𝑚1 = 𝐺 𝑚2 /𝑅2. 𝑎 = 𝐺 𝑚Earth /𝑅Earth2 = (6.67 ⨯ 10-11 N m2/kg2)[(6 ⨯ 1024 kg)/(6.378 ⨯ 106 m)2] = 9.8 m/s2.
Third Law If one object produces a force on a second object, the second object produces an equally strong forces back onto the first object in the opposite direction. These are sometimes called "equal and oppositr forces" and these two forces are act on two different objects.
2.3 Kepler's Laws
First Law The shape of a planet's orbit is an ellipse with the Sun at on focus, so the distance between a planet and the Sun is not, in general, constant.
Second Law An imaginary line between a planet and the Sun sweeps out equal areas in equal times, so planet moves faster when it's in the portion of its orbit closer to the Sun.
Third Law The square of a planet's orbital period is proportional to the cube of the semi-major axis of the planet's orbit, so planets far from the Sun take longer to complete one orbit than planets close to the Sun.
The flatness of an ellipse is called the "eccentricity" of the ellipse. The eccentricity (𝑒) is defined as
(2.5) 𝑒 = √(1 - 𝑏2/𝑎2) = 𝑓/𝑎, 𝑓 = 𝑎𝑒 [𝑎: Semi-major axis, 𝑏: Semi-minor axis]
where 𝑓 is the distance from the center of the ellipse to either focus. For a highly flattened ellipse, the eccentricity approaches one. The point in the planet's orbit that lies closest to the Sun is called the perihelion, and the point farthest from the Sun is called the aphelion.
(2.8) 𝑑𝑖𝑠𝑡𝑎𝑝 = 𝑎 + 𝑓, 𝑑𝑖𝑠𝑡𝑝𝑒𝑟𝑖 = 𝑎 - 𝑓, 𝑑𝑖𝑠𝑡𝑎𝑝 + 𝑑𝑖𝑠𝑡𝑎𝑝 = 2𝑎,
where 𝑑𝑖𝑠𝑡𝑎𝑝 represents aphelion distance and 𝑑𝑖𝑠𝑡𝑎𝑝 represents perihelion distance.
(2.9) 𝑑𝑖𝑠𝑡𝑎𝑝 = 𝑎 + 𝑓 = 𝑎 + 𝑎𝑒 = 𝑎(1 + 𝑒), 𝑑𝑖𝑠𝑡𝑝𝑒𝑟𝑖 = 𝑎 - 𝑓 = 𝑎 - 𝑎𝑒 = 𝑎(1 - 𝑒),
(2.11) 𝑒 = (𝑑𝑖𝑠𝑡𝑎𝑝 - 𝑑𝑖𝑠𝑡𝑝𝑒𝑟𝑖)/2𝑎 = (𝑑𝑖𝑠𝑡𝑎𝑝 - 𝑑𝑖𝑠𝑡𝑝𝑒𝑟𝑖)/(𝑑𝑖𝑠𝑡𝑎𝑝 + 𝑑𝑖𝑠𝑡𝑎𝑝).
Kepler;s Third Law which relates a planet's orbital period (𝑃) to the semi-major axis (𝑎) is often written as
(2.12,13,14) 𝑃2 = 𝑎3 or [𝑃 (in yr)]2 = [𝑎 (in AU)]3 or 𝑃2 = (1 yr2/AU3)𝑎3. [AU: astronomical unit, roughly the distance from Earth to the Sun; 1AU = 149.6 ⨯ 106km]
For example in case of Mars 𝑃 = 687 days = 1.88 yr. So 𝑎 = ([𝑃 (in yr)]2)1/3 = (1.882)1/3 = 1.52 AU.
A more universally applicable version of Kepler's Third Law which is devised Isaac Newton, includes a mass term in the denomenator:
(2.15,16) 𝑃2 = 𝑎3/𝑀 or [𝑃 (in yr)]2 = [𝑎 (in AU)]3/𝑀(in solar masses),
where 1 solar mass = 2 ⨯ 1030 kg. Since the Sun has a mass of 1 solar mass, in case of planets orbiting the Sun we have the same answer in both Eqs.2.12 and Eqs. 2.15.
For example, the orbital period of a satellite in a circular orbit at a distance of 42,164 km from the center of the Earth
𝑎 = 42164 km ⨯ 1 AU/(149.6 ⨯ 106 km) = 2.818 ⨯ 10-4 AU and 𝑀 = the mass of Earth = (6 ⨯ 1024 kg) /(2 ⨯ 1030 kg) = 3 ⨯ 10-6 solar masses
[𝑃 (in yr)]2 = (2.818 ⨯ 10-4)3/(3 ⨯ 10-6) = 7.459 ⨯ 10-6 so 𝑃 = √(7.459 ⨯ 10-6) = 2.73 ⨯ 10-3 yr (= 23 hours and 56 minutes).
There is one more version of Kepler's Third Law
(2.17) 𝑃2 = 4π2𝑎3/𝐺𝑀,
where uses standard (SI) units: 𝑃 in seconds, 𝑎 in meters, 𝑀 in kilogram and 𝐺 is the universal gravitational constant.
3 Light
3.1 Light and spectrum fundamentals
All forms of light are collectively referred to as the "electromagnetic spectrum."The "spectrum" (plural "spectra") refers to the entire range of types of light found in nature. In science the spectrum of an object is a graphical representation of the amount of each color of light present in the object's radiation. The horizontal axis of a spectrum represents the color of light (or one of its proxies such as wavelength, frequency, or energy) and the vertical axis represents the amount of light (which may be called the brightness, intensity, or energy flux). An example of a spectrum is shown in Figure 3.1.
Wavelength (𝜆) Wavelength is the distance between adjacent peaks of the waves (or equivalently, between adjacent valleys). The unit is meters (m).
Frequency (𝑓) Frequency is a measure of the rate at which wave peaks pass a fixed point space. In case of wave, frequency has units of cycles per second. The unit is called the hertz (Hz).
Energy (𝐸) Light waves are made up of tiny bundles of electric and magnetic fields called "photons". Photons and waves are two different but equally valid ways to think about and describe light. The energy of a photon is directly proportional to the frequency of the waves so 𝐸 ∝ 𝑓.
(3.1) 𝜆 = 𝑐/𝑓 or 𝑓 = 𝑐/𝜆 or 𝜆𝑓 = 𝑐. (𝑐: the speed of light in a vacuum, c = 3 ⨯ 108 m/s)
(3.2) 𝐸 = 𝘩𝑓 (𝘩: Planck's constant, 𝘩 = 6.626 ⨯ 10-34 Js)
For example, the frequency and the energy of a photon with 𝜆 = 500 nm (1 nm = 10-9 m) are
𝑓 = 𝑐/𝜆 = (3 ⨯ 108 m/s)/(500 ⨯ 10-9 m) = 3/5 ⨯ 108+7 1/s = 6 ⨯ 1014 Hz and
𝐸 = 𝘩𝑓 = 𝘩(𝑐/𝜆) = (6.626 ⨯ 10-34 Js)(3 ⨯ 108 m/s)/(500 ⨯ 10-9 m) = 3.98 ⨯ 10-19 J.
(3.3) 𝐸 = 𝘩𝑓 = 𝘩(𝑐/𝜆) = 𝘩𝑐/𝜆.
3.2 Radiation laws
The laws which describe the color and the amount of light given off by hot object are called radiation law. The traditional way of referring to the light given off by a hot object is to use the term "blackbody radiation," and objects emitting the kind of light are called "blackbody". Stars behave very much like blackbodies. So although a blackbody is generally not black, does not reflect any light that falls upon it (hence "black"). Instead, a blackbody absorbs all incoming radiation and the all energy of that radiation. This absolved energy contributes to heating the object, which may have its own internal heat sources as well. But it's really useful thing about a blackbody: it emits a very predictable spectrum of radiation with a characteristic shape that depends solely on its temperature. All that matters is the total mount of that energy, which determines the temperature of the blackbody.
As the temperature of a blackbody changes, both the color and the amount of thermal radiation from that blackbody changes, as we can see this in the three thermal-radiation curves. Increasing the temperature of the blackbody causes the wavelengh at which the spectrum reaches it peak (called 𝜆𝑝𝑒𝑎𝑘) to shift toward shorter wavelengths and the height of the peak (that is, the amount of radiation) increases significantly as temperature increases.
Wien's laws The equation that relates an object's temperature (𝑇) to its color is Wien's Law, which can be written like this:
(3.4) 𝜆𝑝𝑒𝑎𝑘 = 𝑏/𝑇,
where the constant we are calling "b" has a value of 𝑏 = 0.0029 m K in SI units (2.9 mm K).
For example, the wavelength of a human being with body temperature of 310 K peak is
𝜆𝑝𝑒𝑎𝑘 = 0.0029 m K/310 K = 2.9 ⨯ 10-3/3.1 ⨯ 102 m = 0.94 ⨯ 10-5 m (= 9.4 μm).
For another example, the temperature of "photoshere (light-emitting layer)" of our Sun whose spectrum peak at about 500 nm is
𝜆𝑝𝑒𝑎𝑘 = 𝑏/𝑇 𝑇 = 𝑏/𝜆𝑝𝑒𝑎𝑘 = 0.0029 m K/ 500 ⨯ 10-9 m = 5,800 K.
Stefan's Laws (Stefan-Boltzman Law) Stefan's Law allows us to calculate the power of radiation produced by each of square meter of that blackbody's emitting surface as a functiion of temperature. That pwer per area is called energy flux (𝐸𝐹), and the Stefan's law is written like this:
(3.6) 𝐸𝐹 = 𝜎𝑇4,
where 𝐸𝐹 has units of watts per square meter (W/m2), 𝜎 is called "Stefan's constant" (𝜎 = 5.67 ⨯ 10-8 W/m2K4), and 𝑇 represents the temperature of the blackbody in kelvins. Some includes a factor called the "emissivity" of the object - but the emissivity of an ideal blackbody is one and most stars are very similar to ideal blackbodies.
The "luminosity" (𝐿) s the total power of the whole object depends not only on the amount of power emitted per unit area, but also on the surface area (𝑆𝐴) from which radiation emitted:
(3.7) 𝐿 = 𝑆𝐴 ⨯ 𝐸𝐹 = (𝑆𝐴)𝜎𝑇4,
For the simplest and most symmetric case of sphere, the surface area is given by 𝑆𝐴 = 4π𝑅2, So the equation for the luminosity of a spherical blackbody with radius 𝑅 and temperature 𝑇 is
(3.8,9) 𝐿 = 4π𝑅2𝜎𝑇4 or 𝐿 ∝ 𝑅2𝑇4.
For example, the luminosity of humanbody with a body temperature of 𝑇 = 310 K and skin surface area of 1.5 m2 is
𝐿 = 𝑆𝐴 ⨯ 𝐸𝐹 = 𝑆𝐴 ⨯ 𝜎𝑇4 ≃ 1.5 m2 (5.67 ⨯ 10-8 W/ m2 K4)(310 K)4 ≈ 785 W.
For another example, if we compare the luminosity of the Earth and Sun: the Sun's photoshere temperature is 5,800 K and Earth's temperature is 290 K, and the Sun's radius is 100 times larger in radius than the Earth, then
𝐿𝑆/𝐿𝐸 = (𝑅𝑆/𝑅𝐸)2(𝑇𝑆/𝑇𝐸)4 = (100)2(5800 K/290 K)4 = (102)2(20)4 = 1.6 ⨯ 109.
This result tells us the Sun is over 1 billion times more luminous than our planet.
Let's think about the difference between the energy flux by a distant blackbody (such as star) and the energy flux received here on Earth. At star, the energy flux from each square meter is 𝐸𝐹 = 𝜎𝑇4 and the total power emitted in all directions is luminosity 𝐿 = 4π𝑅2𝜎𝑇4. The amount of the energy flex reaching Earth (called the "apparent brightness" of the star) depends not only on the luminosity of the star which is the total power given off and but also on the distance from the star to the Earth, that is, at Earth energy flux received on each square meter is luminosity/4π(distance)2. So we have the equation
𝐸𝐹 = 𝐿/(4π𝐷2)
where 𝐸𝐹 is the apparent brightness of the star and 𝐷 is the distance from the star to the Earth.
The difference between the energy flux emitted by a blackbody and the energy flex received by an observer can be seen in Figure 3.8. The curves in the left portion of this figure represent the emitted by the blackbodies of different temperatures. According to Wien's Law The blackbody 1 reaches a peak at a shorter wavelength than the others. And according to Stefan;s Law that blackbody 1 is hotter than the others. When we can see in the right portion of the figure since the the received flux depends on the distance of the blackbody from Earth and the total power radiated by the blackbody these curves cannot be used to determine the temperature of the blackbodies.
But because Wien's Law tells us that 𝜆𝑝𝑒𝑎𝑘 is inversely proportional to temperature, so the shorter the peak is the high the temperature is, therefore blackboody 2 has a lower temperature than blackbody 1. The same analysis applied to the other curves and the blackbody 3 is cooler than blackbody 2 and it might be bigger or closer than the other blackbodies.
3.3 Doppler shift
One of the powerful tools for astronomer called "Doppler shift" is the ability to measure the speed with which an object is moving toward or away from the Earth. It works for any object that's emitting or reflecting electromagnetic waves. If the source of the wave is moving away from us, the waves appears stretched out and the wave crests and troughs arrives less frequently than if the source were stationary. So for a receding source we measure a longer wavelength a lower frequency than the true value.
Since the blue light has shorter wavelength and higher frequency than red light the light from approaching objects is said to be "blueshifted" and the light from receding objects is said to be "redshifted". In astronomy, this terminology used even if the wave are not visible portion of spectrum of such as radio waves or X-rays. All that matters is the relative speed between us and the source.
Doppler-shift equation may be written
(3.10) 𝜆𝑎𝑝𝑝/𝜆𝑡𝑟𝑢𝑒 = 1 + 𝜐𝑟𝑒𝑐/𝑐,
where 𝜆𝑎𝑝𝑝 is the wavelength measured by the observer, 𝜆𝑡𝑟𝑢𝑒 the wavelength given off by the source, 𝜐𝑟𝑒𝑐 is the recession speed (defined as the speed with which an object is moving away from the observer and 𝑐 is the the speed of light in empty space. Since 𝜐𝑟𝑒𝑐 is the speed of recession its value is posiitive if the source and observer are getting father apart (receding) and negative if they're getting closer together (closing).
For example, if a start moving awy from the Earth on a speed of 300 km/s and the star is emitting radiation at a wavelength of 530 nm, then the wavelength measured by an observer on Earth is
𝜆𝑎𝑝𝑝 = 𝜆𝑡𝑟𝑢𝑒(1 + 𝜐𝑟𝑒𝑐/𝑐) = (530 nm)[1 + (300 km/s)/(3 ⨯ 105 km/s)] = 530.53 nm.
Fortunately astronomers know the exact wavelength of many spectral lines with extreme precision, and tiny shift in those spectral lines have been used to measure Doppler shift from objects moving at speed of less than 1 m/s relative to the Earth.
Another useful form of the Doppler-shift equation can br obtained by re-arranging Eq. 3.10
𝜆𝑎𝑝𝑝/𝜆𝑡𝑟𝑢𝑒 = 1 + 𝜐𝑟𝑒𝑐/𝑐
𝜆𝑎𝑝𝑝 = 𝜆𝑡𝑟𝑢𝑒 + 𝜆𝑡𝑟𝑢𝑒(𝜐𝑟𝑒𝑐/𝑐), (𝜆𝑎𝑝𝑝 - 𝜆𝑡𝑟𝑢𝑒)/𝜆𝑡𝑟𝑢𝑒 = 𝜐𝑟𝑒𝑐/𝑐 Designating (𝜆𝑎𝑝𝑝 - 𝜆𝑡𝑟𝑢𝑒) as 𝛥𝜆, this becomes
(3.11) 𝛥𝜆/𝜆𝑡𝑟𝑢𝑒 = 𝜐𝑟𝑒𝑐/𝑐,
which tells us that the fractional change in wavelength is equal to the fraction of the the speed of light at which the object is receding. For the previous example,
𝛥𝜆/𝜆𝑡𝑟𝑢𝑒 = 𝜐𝑟𝑒𝑐/𝑐, 𝛥𝜆 = 𝜆𝑡𝑟𝑢𝑒 𝜐𝑟𝑒𝑐/𝑐 = 530 nm[(300 km/s)/(3 ⨯ 105 km/s)] = 0.53 nm.
Also we may encounter a version of the Doppler-shift equation involves frequencies instead of wavelengths. Then we must remember
𝜆𝑎𝑝𝑝𝑓𝑎𝑝𝑝 = 𝑐 and 𝜆𝑡𝑟𝑢𝑒𝑓𝑡𝑟𝑢𝑒 = 𝑐, then
𝜆𝑎𝑝𝑝/𝜆𝑡𝑟𝑢𝑒 = (𝑐/𝑓𝑎𝑝𝑝)/(𝑐/𝑓𝑡𝑟𝑢𝑒) = 1 + 𝜐𝑟𝑒𝑐/𝑐,
(3.12) 𝑓𝑡𝑟𝑢𝑒/𝑓𝑎𝑝𝑝 = 1 + 𝜐𝑟𝑒𝑐/𝑐.
We should notice that frequency and wavelength are inversely proportional, We can also find an expression for fractional change in frequency as follows,
𝑓𝑡𝑟𝑢𝑒/𝑓𝑎𝑝𝑝 = 1 + 𝜐𝑟𝑒𝑐/𝑐
𝑓𝑡𝑟𝑢𝑒 = 𝑓𝑎𝑝𝑝(1 + 𝜐𝑟𝑒𝑐/𝑐), (𝑓𝑡𝑟𝑢𝑒 - 𝑓𝑎𝑝𝑝)/𝑓𝑎𝑝𝑝 = 𝜐𝑟𝑒𝑐/𝑐, if we designate 𝛥𝑓 as (𝑓𝑎𝑝𝑝 - 𝑓𝑡𝑟𝑢𝑒), then
(3.13) -𝛥𝑓/𝑓𝑎𝑝𝑝 = 𝜐𝑟𝑒𝑐/𝑐, or 𝛥𝑓/𝑓𝑎𝑝𝑝 = -𝜐𝑟𝑒𝑐/𝑐.
3.4 Radial-velocity plots
The Doppler effect is the basis for one of the most effective tools used by astronomers searching for planets orbiting around stars other than the Sun. It's possible to detecting extrasolar planets indirectly by measuring the effect of a planet's gravitational pull on its parent star. the effect comes about from the second modification Newton made to Kepler's Laws. Newton's second modification is that both the planet and the sun orbits a point called the "center of mass" of the Sun-planet system.
In reality stars are so much more massive than planets that in many cases the enter of mass between the star and planet is located at a point inside the star and the star wobbles around somewhat between the center and its outer layer.
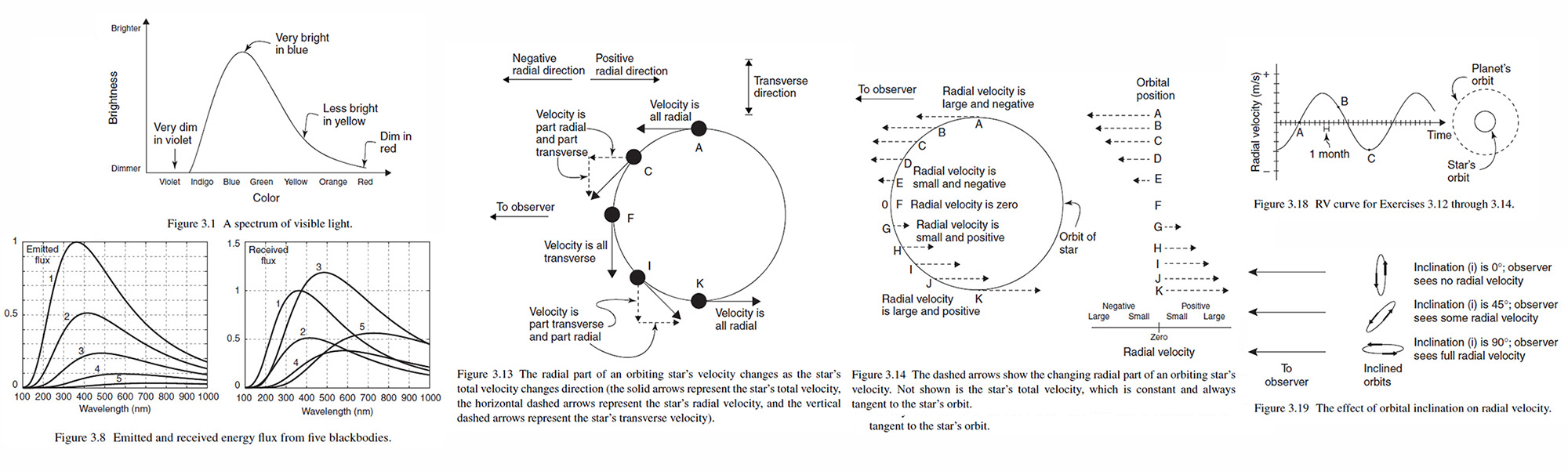
We may notice that the radial direction is defined as the direction along the observer's line of sight, and the traverse direction is defined as the direction perpendicular to the observer's line of sight. Radial and transverse velocity are important to understand the observations of orbiting stars, as illustrated in Figure 3.13 which depicts the circular orbit of a star as observed by a distant observer. The relevance of the changing radial velocity of an orbiting star is that the Doppler shift of the light will go from a relatively strong blueshift at A, so a smaller blueshift at C, to zero shift at F, and then small redshift at I and relatively strong redshift at K. This changing Doppler shift is the hallmark of a star being orbited by a planet.
In Figure 3.15 the lengths of the dashed horizontal arrows indicate the magnitude of the radial velocity only. Even more instructive are the plots of an example in Figure 3.18, in which a radial-velocity plot (RV plot) varies sinusoidally with the spacing of time (month) on the horizontal axis and the radial velocity (m/s) on the vertical axis. We should be aware that the higher the eccentricity of the star's orbit the more asymmetrical, which means the orbit is somewhat elliptical. If we use Newton's modified version of Kepler's Third Law (𝑃2 = 𝑎3/𝑀) the semi-major axis (𝑎) of the planet's orbit may be found with the information of the star's mass (𝑀) which may be estimated from Herzsprung-Rusell diagram in Section 5.4 later and the planet's orbital period (𝑃) determined from the RV plot.
Finally because of the effect of orbital inclination as shown in Figure 3.19 we often use "𝑀 sin 𝑖", where 𝑀 is unknown planets mass and 𝑖 is the unknown angle of inclination of the orbit. If 𝑖 = 0∘, no Doppler shift would be detected, and 𝑀 sin 0∘ = 0 correspond to "no planet found," If 𝑖 = 90∘, the orbit is viewed edge-on and the full mass is inferred. So
𝑀inferred = 𝑀actual sin 𝑖
which means
(3.14) 𝑀actual = 𝑀inferred/sin 𝑖,
where 𝑀actual is bigger than 𝑀inferred is the minimum possible mass of the planet. In rare cases, a planet is observed to"transit" its parent star. This means that the orbital plane is aligned so precisely with our viewing angle. In such case the radial-velocity plot is known to show nearly the full Doppler, shift and the inferred planet mass is known to be nearly the full planet mass.
* Textbook: D. Fleisch & J. Kregenow A Student's Guide to the Mathematics of Astronomy (Cambridge University Press 2013)
p.s. 천문학의 기초적 수학을 다룬 이 책은 저와 같은 완전 초보자들에게 대단히 유용하므로
몇년 전에 읽은 책이기는 하지만 앞날의 참고를 위해서 이곳에 요약 정리해 놓을 필요가 있을 듯 ...
이는 Mathematical Cosmology와 Mukhanov's Cosmology에 필요한 최소 사전 지식으로 생각되는
Kepler의 법칙과 Stefan의 법칙을 비롯해 우주의 미래 팽창률까지 필수 공식들을 잘 설명함.
(몇년 전에 작성한 내용에서 오류가 여러 군데 발견되어 수정 및 보충하여 업데이트함.) |
|
|