|
김관석
|
2023-04-06 09:30:39, 조회수 : 256 |
- Download #1 : MA_Fig_4.jpg (324.8 KB), Download : 5
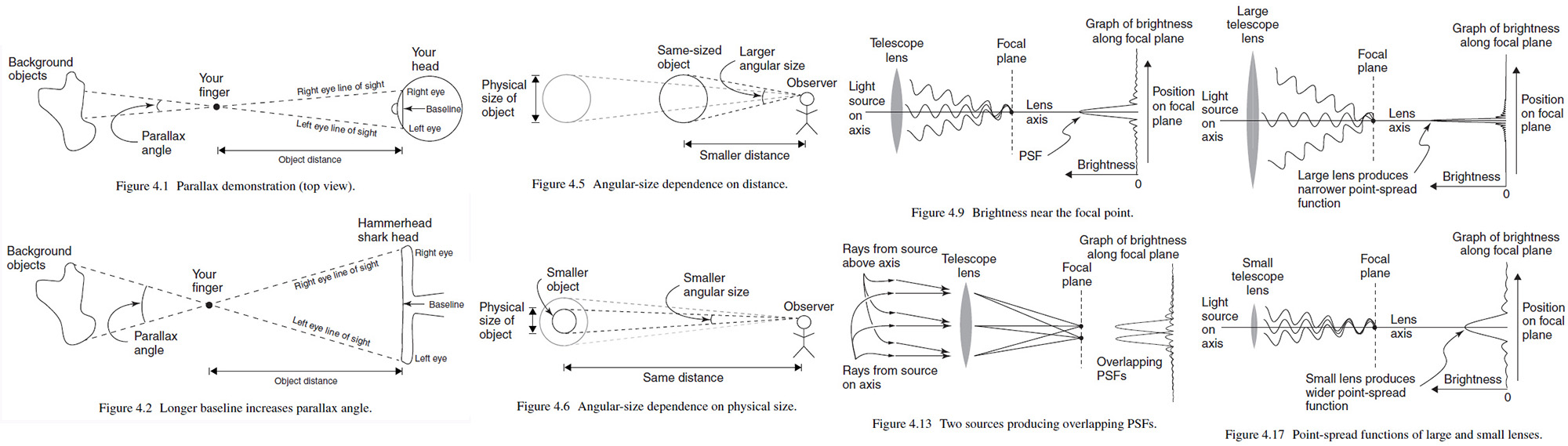

4 Parallax, angular size, and angular resolution
4.1 Parallax
Parallax is a perspective phenomenon that makes a nearby object appear to shift position with respect to more distant objects when the observation point is changed.
As illustrated in Figure 4.1 the amount of the shift, measured as an angle, is called the parallax angle. And those very different lines of sight would make the parallax angle bigger for an object at a given distance as shown in Figure 4.2. By comparing the parallax angle in Figure 4.1 and 4.2, you can see that greater separation between observation points increase the parallax angle for an object at any given distance. The separation between observation points is called the "baseline" of the parallax measurement. In fact the tangent of the parallax angle is directly proportional to the baseline. But for angles less than about 10∘ the tangent of an angle and the value of the angle (in radians) are same to within about 1%. In astronomy, you'll encounter are fraction of a degree, so this approximation is useful. (Some astronomy texts define the stellar parallax angle as half of the angle by which the objects shifts considering the half of baseline as described in Section 5.1.)
So we obtain
(4.1) parallax angle ∝ (base line/object distance) or
(4.2) parallax angle = (const) ⨯ (base line/object distance),
where the constant will be 1.0 as long as the units of the baseline and the object distance are same and the units of the parallax angle are radians. We can build the conversion factor from radians to degrees as follows
(4.3) parallax angle (deg) = 57.3∘ ⨯ (base line/object distance),
where the factor of 57.3 (which is 180/π) does the conversion from radians to degrees, because 180∘ = π radians.
For example, Using a baseline of 20m, a surveyor measures a parallax angle of 2.4∘ for a distant tree, We can find the distance
object distance = 180 deg/π (baseline/parallax angle (deg)) = 57.3∘(20 m/2.4∘) = 477.5 m.
4.2 Angular size
Angular size depends on both the physical size of the object and the distance to the observer as shown in Figure 4.4 and Figure 4.5.
(4.4) angular size ∝ (Physical size/distance) or
(4.5) angular size = (const) ⨯ (Physical size/distance)
(4.6) angular size (rad) = [Physical size (same units as distance)]/[distance (same units as distance)]
For example, the diameter of a planet whose angular size is 47" as seen from the Earth when the distance to the planet is 4.2 AU? is
angular size = 47" ⨯ [1 degree/3,600"] ⨯ [π radians/180 degrees] = 2.28 ⨯ 10-4 rad.
distance = 4.2 AU ⨯ [1.5 ⨯ 108 km/1 AU] = 6.3 ⨯ 108 km.
(4.7) physical size = (angular size)(distance). So
physical size = (angular size)(distance) = (2.28 ⨯ 10-4 rad)(6.3 ⨯ 108 km) = 143,640 km
which is the diameter of the planet Jupiter.
(4.8) angular size(deg) = 180 deg/π ⨯ [Physical size/distance] = 57.3∘[Physical size/distance].
4.3 Angular resolution
Angular resolution is the minimum angle over which two points may be seen as separate rather than blurred together. Resolution is related th the wave nature of light. When two ore more waves are present at the same location, the interaction between these waves is called "interference".
We should notice when two waves are in step (also called "in phase"), the add constructively to produce a larger wave. But if those are out of step, they add destructively to produce a smaller wave. And if the waves are just slightly out of step. the resultant wave is not as big as the perfectly in-step case, but it is still bigger than either of the constituent waves. As we can see in Figure 4.9, the waves from astronomical objects after passing through the lens converge toward a "focal point" which is on the lens axis (the angles are exaggerated for clarity) at a "focal plane".
It's important to understand that at the focal point all the waves on the lens are all in step. This means that the waves produce a bright spot on the image and over a small region the waves add constructively. That graph wth a large central peak surrounded by lots of little bumps is called the "point-spread function" (PSF) because it shows how the light from a single source point is spread out one the image. We should also notice that there are series of "nulls" between the minor peaks. We should understand that the light is spread over a small region and the bigger that region, the "fuzzier" the image looks. The ring pattern is called "Airy pattern" and bright central spot is called the "Airy disk". (Both are named after George Biddell Airy.)
Now we can consider what happens when the waves from two sources strikes the at he same time as shown in Figure 4.13. In this case The two PSFs might be sufficiently separated and these two sources are said to be "resolved". When the two PSF is at least as great as the separation between the peak and the first null of a single PSF the case meets the "Rayleigh criterion" (defined by Lord Rayleigh). Meeting the Rayleigh criterion ensures that an observer can recognize that there are two separate sources.
The final concept you need to consider before you can understand the equation for angular resolution based on the Rayleigh criterion was that the dith of the PSF depends on the wavelength of the light and the size of the lens or mirror. For any given wavelengh, the larger the lens, the narrower the PSF. So a telescope with a large aperture produces a narrower PSF than a telescope with a smaller aperture, as shown in Figure 4.17, because larger lens have greater distance from the center to the edge of the lens, and the greater that distance, the less angle it takes cause the edge waves to get out of step with the center waves. This means that the angular resolution of a telescope is inversely proportional to the aperture:
(4.9) angular resolution ∝ 1/aperture.
The width of the PSF also depends on the wavelength(𝜆) of light use, because the shorter the wavelength, the smaller angular shift it takes to make the edge waves get out of step with the center waves. This means:
(4.10) angular resolution ∝ 𝜆.
Combining the Eqs. 4.9 and 4.10 gives:
(4.11) angular resolution ∝ 𝜆/aperture, or
(4.12) angular resolution = (const) ⨯ [𝜆 /aperture].
If angular resolution is expressed in the radian, the constant of proportionality in Eqs. 4.12 is approximately 1.22 for a circular lens. Thus
(4.13) angular resolution (rad) = 1.22 ⨯ [𝜆 (same units as aperture) / aperture (same units as 𝜆)].
For example, a telescope with a 10-inch lens is used to observe celestial objects. The angular resolution of this telescope in the middle of visible range is:
The wavelength of visible light range from around 400 nm to 700 nm, so the average is about 550 nm, so
𝜆 = 550 nm = 550 ⨯ 10-9 m = 5.5 ⨯ 10-7 m and aperture = 10 in - 10 ⨯ 0.0254 m = 0.254 m
angular resolution (rad) = 1.22 ⨯ [5.5 ⨯ 10-7 m/0.254 m] 2.64 ⨯ 10-6 radians, which can be coverted to arcseconds as follows:
2.64 ⨯ 10-6 radians = 2.64 ⨯ 10-6 radians ⨯ [180 degrees/π radians] ⨯ [3,600"/1 degree] = 0.54 arcseconds.
Since wavelength is usually expressed in arcseconds:
(4.14) angular resolution (arcsec) = 0.25 [𝜆(𝜇m)/aperture(m)].
* Textbook: D. Fleisch & J. Kregenow A Student's Guide to the Mathematics of Astronomy (Cambridge University Press 2013) |
|
|





































