|
김관석
|
2023-04-18 14:41:13, 조회수 : 838 |
- Download #1 : MA_Fig_5.jpg (292.4 KB), Download : 5
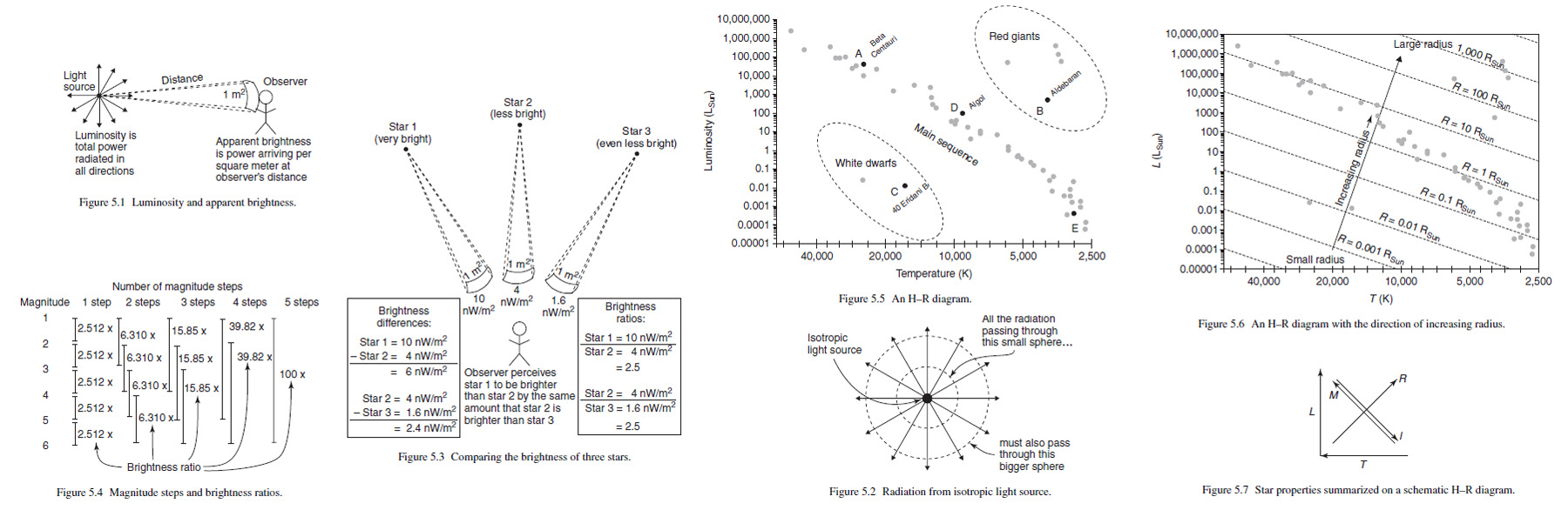

5 Stars
By taking starlight apart using spectrographs and making precise measurements of its brightness, we've come to understand a great deal not only about nature of stars, but also about the structure and workings of the Universe at large. The mathematics behind that understanding is the subject of this chapter.
5.1 Stellar Parallax
As the Earth moves from one side of its orbit to the other over the course of half a year, star's resulting angular shift and its distance from Earth are related by this equation:
(5.1) 𝑑 = 1/𝑝,
where 𝑑 is the distance to the star in units of parsecs (pc), and 𝑝 is the parallax angular shift in units of arcsecond ("). 1 pc = 3.09 ⨯ 1013 km = 3.26 light years (ly) and 1" = 1/3600 degree.
For example, for the star Alcor the parallax angle = 0.04", then the distance from the Earth to Alcor is
𝑑 = 1/𝑝 - 1/0.04 = 100/4 = 25 pc.
We can rearrange Eq. 5.1 to solve foe the parallax angle 𝑝:
(5.2) 𝑝 = 1/𝑑.
For example. Polaris (the North star) is 434 light years away, then the parallax angle is
𝑝 = 1/𝑑 = 1/434 ly ⋅ (3.25 ly/ 1 pc) = 3.26/ 434 arcsec = 0.0075"
This angle 7.5 milliarcseconds is readily detectable by modern research telescopes.
If we only need to compare two quantities rather than calculating an absolute number, then the ratio method can save you time and effort.
For example, the nearest star to the Earth after the Sun is Proxima Centauri, at about 4 ly. Polaris's distance is 100 times larger than Proxima's distance, their parallax angle can be compared as follows
(𝑑𝑃𝑟𝑜𝑥𝑖𝑚𝑎 = 1/𝑝𝑃𝑟𝑜𝑥𝑖𝑚𝑎)/(𝑑𝑃𝑜𝑙𝑎𝑟𝑖𝑠 = 1/𝑝𝑃𝑜𝑙𝑎𝑟𝑖𝑠) → 𝑑𝑃𝑟𝑜𝑥𝑖𝑚𝑎/𝑑𝑃𝑜𝑙𝑎𝑟𝑖𝑠= 1/𝑝𝑃𝑟𝑜𝑥𝑖𝑚𝑎 ⨯ 𝑝𝑃𝑜𝑙𝑎𝑟𝑖𝑠/1,
(5.3) 𝑑𝑃𝑟𝑜𝑥𝑖𝑚𝑎/𝑑𝑃𝑜𝑙𝑎𝑟𝑖𝑠= 𝑝𝑃𝑜𝑙𝑎𝑟𝑖𝑠/𝑝𝑃𝑟𝑜𝑥𝑖𝑚𝑎.
Now we can translate the given information" Polaris's distance is 100 times larger then Proxima's distance:
𝑑𝑃𝑜𝑙𝑎𝑟𝑖𝑠 = 100 𝑑𝑃𝑟𝑜𝑥𝑖𝑚𝑎 so 𝑝𝑃𝑜𝑙𝑎𝑟𝑖𝑠 = 1/100 𝑝𝑃𝑟𝑜𝑥𝑖𝑚𝑎.
5.2 Luminosity and apparent brightness
The "luminosity" of an object is defined as the amount of power radiated by an object, with SI units if watts. In contrast the "apparent brightness" of the light source involves both luminosity of the object and the distance between the source and the observer, with SI units of watts per square meter as seen in Figure 5.1. The apparent brightness is a measure not of power, but of received energy flux, which is called "power density" by engineers. The actual received power for any one observer depends on the aperture of the observing system (or the pupils of the observer's eyes).
For example, if the energy flux at some distance form a light source is 20 microwatts per square meter and our optical system has an aperture area of one-tenth of a square meter, we'll receive one-tenth of 20 microwatts, which is 2 microwatts.
Experiments have shown that the intensity of radiation varies inversely proportional to the square of the distance. So we have
(5.4) apparent brightness ∝ 1/𝑑𝑖𝑠𝑡2.
Experiments also reveal that power density is directly proportional to the luminosity of the light source. Thus
(5.5) apparent brightness ∝ 𝐿.
Combining the proportionality relationships of Eqs. t,4 and 5.5 gives
(5.6) apparent brightness ∝ 𝐿/𝑑𝑖𝑠𝑡2 or
(5.7) apparent brightness = const ⨯ (𝐿/𝑑𝑖𝑠𝑡2).
The case of a light source that radiates equal power in all directions: such a source is called "isotropic." The radiation from an isotropic light source is shown in Figure 5.2. In this figure, the dashed circles represent two imaginary spheres surrounding the isotropic light source, and the arrows represent radiation emanating from the source in all directions (three-dimensionally) outward. Because the total power (the number of watts) hitting both spheres must be the same. Since energy flux is defined as the power per unit area, the apparent brightness of the source for an observer at the inner sphere is
(5.8) (apparent brightness)inner = 𝐿/𝑆𝐴𝑖𝑛𝑛𝑒𝑟 𝑠𝑝𝘩𝑒𝑟𝑒.
where 𝑆𝐴 = the surface area. Since the source area of a sphere is 4π times the radius (𝑅) of the sphere squared, this is
(5.9) (apparent brightness)inner = 𝐿/4𝜋(𝑅𝑖𝑛𝑛𝑒𝑟)2.
Likewise, for an observer at the outer sphere, the apparent brightness is
(5.10) (apparent brightness)outer = 𝐿/4𝜋(𝑅𝑜𝑢𝑡𝑒𝑟)2.
So both Eqs. 5.9 and Eqs. 5.10 can be written more generally as
(5.11) apparent brightness = 𝐿/4𝜋(𝑑𝑖𝑠𝑡)2.
For example, The Sun's luminosity is approximately 4 ⨯ 1026 W and its distance from Earth is about 150 million kilometers. Ignoring reflection by clouds and absorption in the Earth's atmosphere, the apparent brightness of the Sun at the surface of the Earth is
apparent brightness = 𝐿/4𝜋(𝑑𝑖𝑠𝑡)2 = 4 ⨯ 1026 W /4𝜋(1.5 ⨯ 1011 m)2 = 1415 W/m2.
This is called the "solar constant" at Earth.
5.3 Magnitudes
In addition it the quantities of apparent brightness and luminosity, astronomers have another system of classifying the brightness of celestial objects. That system is called the "magnitude" system, and it's based on the way the human eye sees different intensities of light. We'll explain the two main types of magnitude. "Apparent magnitude" is related to the apparent brightness of a light source. "Absolute magnitude" is related to the intrinsic brightness, or luminosity of the source.
The apparent magnitude scale was introduced over 2,000 years ago by the Greek astronomer Hipparchus, who grouped the stars into six categories. He lumped the 20 or so brightest stars into the category called "first magnitude", slightly dimmer but bright stars into "second category, Medium-brightness stars into "third magnitude", dim stars into "fourth magnitude", very dim stars "fifth magnitude" and barely visible stars into "sixth magnitude".The apparent magnitude of a celestial object often denoted as "𝑚." Hipparchus's first-magnitude group comprises constellations such as Orion or the Southern Cross, most of the stars in Big Dipper would belong to the second-magnitude group and the Little Dipper would span from second to fourth or fifth magnitude. In today's light-polluted skies, the sixth-magnitude category are invisible from all but the very best observing sites.
When scientists began to make quantitative measurements of the brightness of light source, they discovered an interesting fact: the apparent magnitude operate in a logarithmic fashion rather than linear one. In Figure 5.3 when we are looking at three stars in Hipparchus's first-magnitude, second-magnitude and the third-magnitude, measurement reveal that in fact 𝑚 = 2 star are about 2.5 times dimmer than 𝑚 = 1 star, and 𝑚 = 3 star are about 2.5 times dimmer than 𝑚 = 2 star. So the ratio of brightness categories is constant but the difference is not.
In the 19th century, British astronomer Norman Robert Pogson suggested that five steps in magnitude should correspond exactly to factor of 100 in brightness. Thus the brightness ration corresponding to one magnitude step should be 3√100 = 2.512. Fig. 5.4 illustrates the relationship between magnitude steps and brightness ratios. So we have an equation like this:
(5.12) brightness ratio = (2.512)# mag steps,
where "# mag steps" (𝛥𝑚) represents the number of magnitude steps between the two object.
For example, the apparent magnitude of Altar in the constellation of Aquila is 𝑚 = 0.77, and Merak in the Big Dipper is 𝑚 = 2.36, then the brightness ration is
brightness ratio = (2.512)(2.36 - 0.77) = (2.512)1.59 = 4.325,
so Altair is a little over four times brighter than Merak.
Start by taking the logarithm (base 10) of both side of Eq. 5.12:
(5.13) log10(brightness ratio) = log10[(2.512)𝛥𝑚].
Because the log(𝑥𝑎) = 𝑎 log(𝑥), log10(brightness ratio) = 𝛥𝑚 log10[(2.512)] or
(5.14) 𝛥𝑚 = log10(brightness ratio)/log10(2.512).
For example, a certain star is 100 times dimmer than a star of 𝑚 = 1, the apparent magnitude of the dimmer star is
𝛥𝑚 = log10(100)/log10(2.512) = 2/0.4 = 5.0,
so the dimmer star is of 𝑚 = +6.
Since optical instruments allows us to see faint objects, astronomer have extended the apparent magnitude system beyond the six categories of Hipparchus. So a a star that is 2.512 times dimmer than a star of 𝑚 = +6 is assigned 𝑚 = +7, and so on.And a star that's 2.512 times brighter than a star with 𝑚 = +1 is a star of 𝑚 = 0 and a star that's one magnitude step brighter than a 0-magnitude star must have 𝑚 = -1.
The next step is to understand absolute magnitude (often written as "𝑀") which is just the apparent magnitude the object would have if it were a distance of 10 parsecs.
For example, at a distance of 1 AU from the Earth, the Sun has 𝑚 = -26.8, then the Sun's absolute magnitude is
10 pc = 10 ⨯ [206,265 AU/1 pc] = 2.06 ⨯ 106 AU.
distance ratio - 10 pc/1 AU = 2.06 ⨯ 106 AU/1 AU = 2.06 ⨯ 106.
Because the brightness is proportional to 1/(𝑑𝑖𝑠𝑡)2, so the brightness decreases by a factor of 1/(2.06 ⨯ 106)2 = 1/4.25 ⨯ 1012. According to Eq. 5.14
𝛥𝑚 = log10(4.25 ⨯ 1012)/log10(2.512) = 12.63/0.4 = 31.6.
So the Sun's absolute magnitude is:
(5.15) 𝑀𝑆𝑢𝑛 = -26.8 + 31.6 = +4.8.
Now if we know an object's apparent magnitude (𝑚) and its absolute magnitude (𝑀) we can calculate the distance of the object. The difference between these quantities is called the "distance modulus" (𝐷𝑀), and it is related to the distance (𝑑, measured in units of parsecs) by equation:
(5.16) 𝐷𝑀 = 𝑚 - 𝑀 = 5log10[𝑑/10pc]
which can be solved for distance:
10𝐷𝑀/5 = 𝑑/10pc 𝑑 = 10 pc ⨯ [10𝐷𝑀/5] = [10𝑚 - 𝑀/5].
(5.17) 𝑑 = 10pc ⨯ [10𝐷𝑀/5] = 10pc ⨯ [10(𝑚 - 𝑀)/5].
For example, The star Denebola is known by parallax measurements to lie about 36 light years from Earth, and its apparent magnitude is 2.1, the the its absolute manignitude is
𝐷𝑀 = 𝑚 - 𝑀 = 5log10[𝑑/10pc]
(5.18) 𝑀 = 𝑚 - 5log[𝑑/10pc].
Since the distance must be in units of parsecs
36 ly = 36 ⨯ [1 pc/3.26 ly] = 11 pc 𝑀 = 𝑚 - 5log[𝑑/10pc] = 2.1 - 5 log10[11 pc/10 pc] = 2.1 - 5log10(1.1) = 1.9.
This is just a bit smaller than Denebola's apparent magnitude, as expected for a star that's just a bit father than 10 pc from Earth.
For example, A variable star in the Andromeda Galaxy is measured to have an apparent magnitude of +18.5 and an absolute magnitude (which can be determined form its period of variation) of -6. So the distance of the Andromeda Galaxy from Earth is
𝐷𝑀 = 𝑚 - 𝑀 = 18.5 - (-6) = 24.5
𝑑 = 10pc ⨯ [10𝐷𝑀/5] = 10 pc ⨯ [1024.5/5] = 10 pc ⨯ [104.9] = 10 pc ⨯ (79,432.8) = 794,328 pc,
which is over 2.5 million light years. (In 1924 Hubble found 36 variable stars in Andromeda, 12 of which were Cepheids. Using them he obtained a distance 900,000 light years. Improved measurements now place Andromeda at approximately 765 kpc(2.5 million light years) away from Earth.)
5.4 H-R diagram
The Hertzsprung-Russel (H-R) diagram is a graph of two properties luminosity and temperature of many stars. Many dots on an H-R diagram represent stars, which remain fixed for the vast majority of their lives. For most stars, that location falls on abroad swath running from the upper left to the lower right portions of the star diagram; this is called the "main sequence," and it encompasses most of stars plotted in Figure 5.5. The few stars that are not on the main sequence generally occupy regions in either the upper right, called "red giants", or lower left, called "white dwarfs."
The two star properties on the H-R diagram are luminosity (𝐿) and (surface) temperature (𝑇). However, there are three other stellar properties- star radius (𝑅), lifetime (𝓵), and mass (𝑀). Because H-R diagram represents all five of these fundamental stellar properties in one compact graphs, it is such a powerful tool in astronomy.
In order to express physical quantities more intuitively, astronomers employ a set of "solarcentric" units that use our Sun's properties as a reference. The subscript ⊙ is frequently used to indicate a parameter pertains to the Sun, so "M⊙" means "MSun". The three most-common solarcentric units are solar luminosities ("L⊙" or "LSun"), solar radii ("R⊙" or "RSun"), and solar mass ("M⊙" or "MSun"). Here are the equivalence relations for them:
1 M⊙ (solar mass) ⟷ 2 ⨯ 1030 kg,
1 L⊙ (solar luminosity) ⟷ 4 ⨯ 1026 W,
1 R⊙ (solar radius) ⟷ 6.96 ⨯ 105 km.
(MEarth ⟷ 6.0 ⨯ 1024 kg ≈ 3.0 ⨯ 10-6 M⊙ or M⊙ = 3.3 ⨯ 106 MEarth, and REarth ⟷ 6.37 ⨯ 103 kg ≈ 1.09 ⨯ 10-2 M⊙ or R⊙ ≈ 109 ⨯ REarth.)
It is instructive to show relationship among star's radius, luminosity and surface temperature:
(5.19) 𝑅2 ∝ 𝐿/𝑇4.
For example, if we rank the labeled stars in Figure 5.5 in order of increasing size, we can have Figure 5.6.
So the ranking of all five from smallest to largest id C < E < D < A < B.
Some texts quote a quantitative relationship between main-sequence star mass and luminosity similar to the following:
(5.20) 𝐿 ∝ 𝑀3.5,
which indicates that stars with larger mass also have larger luminosity. Note that the value of exponent varies between 3.0 to 4.0 for different regions on the main sequence star, but be aware that other texts may use a slightly different value.
The "lifetime" of a star is usually defined as the time that star spends fusing hydrogen into helium in its core. That time is determined by the amount of hydrogen fuel initially in the star' core and the rate at which the star uses that fuel. The mathematical relationship between lifetime and mass can be seen by the assumption that a main-sequence star's available fuel is proportional to its mass (amount of fuel ∝ 𝑀) and Eqs. 5.20 we can describe:
lifetime = (amount of fuel)/(rate of fuel use) ∝ 𝑀/𝐿 ∝𝑀/𝑀3.5 ∝ 𝑀1 - 3.5 ∝ 𝑀2.5.
(5.21) 𝓵 ∝ 𝑀-2.5 or 𝓵 ∝ 1/𝑀2.5 or 𝓵 ∝ (1/𝑀)2.5.
For example, the main-sequence lifetime of a 6 M⊙ star is (the Sun's lifetime is about 10 biilion years)
𝓵star/𝓵Sun = (𝑀star/𝑀Sun)-2.5 = (6M⊙/M⊙)-2.5 = (6)-2.5 = 0.01, or
𝓵star = 0.01 ⨯ (1010 years) = 100 million years.
We may sketch a bare-bones H-R diagram with arrows indicating the the direction in which each of parameters increases. Figure 5.7 shows arrows indicating the direction of all five properties of stars discussed in this section.
* Textbook: D. Fleisch & J. Kregenow A Student's Guide to the Mathematics of Astronomy (Cambridge University Press 2013) |
|
|





































