|
김관석
|
2023-05-02 08:31:40, 조회수 : 589 |
- Download #1 : MA_Fig_6.jpg (356.4 KB), Download : 5
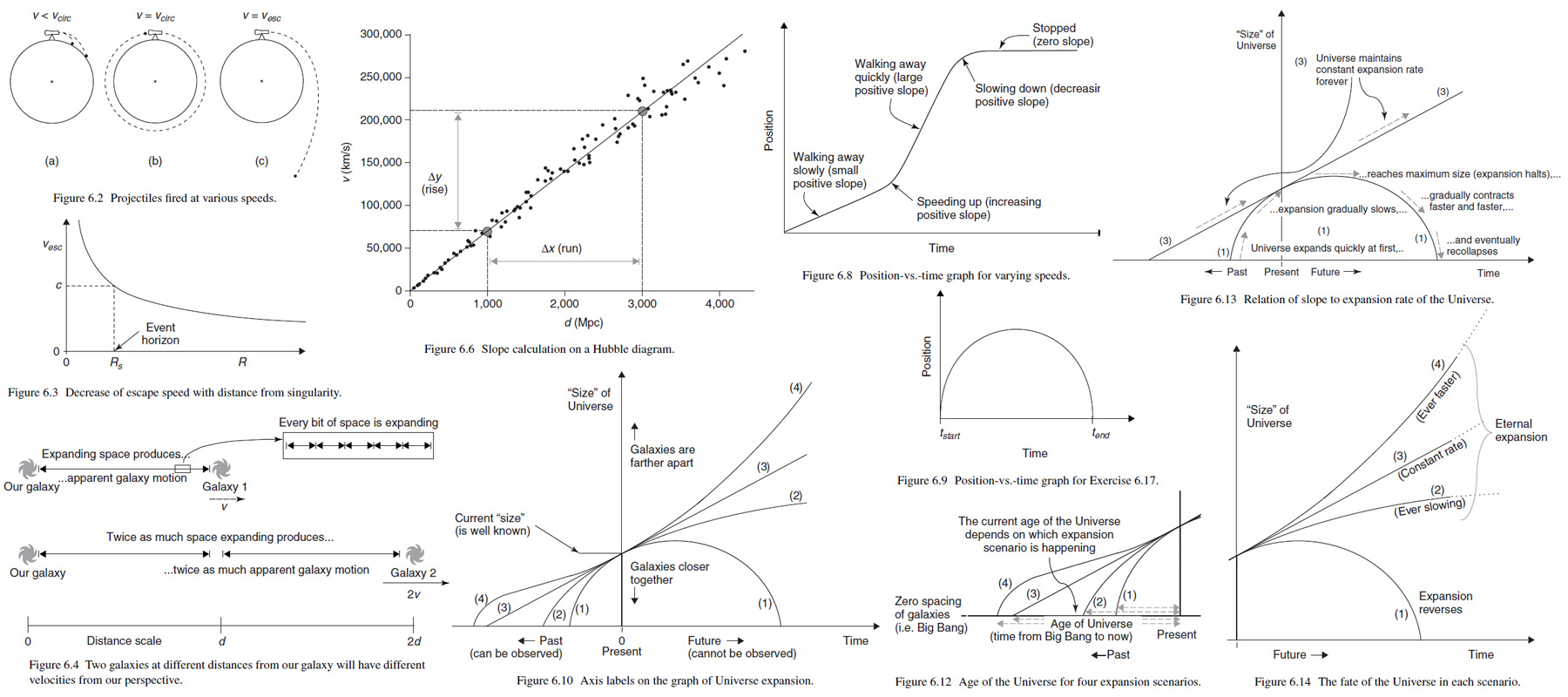

6 Black holes and cosmology
This chapter deals with “limiting cases” by investigating the mathematical ramifications of taking one variable to an extreme, such as allowing the radius of an object to shrink to zero or permitting time to run to infinity. The physical manifestations of these mathematical limiting cases lead to the most exotic concepts in astronomy: black holes, which are singularities of mass; and cosmology, which deals with the history and fate of the Universe.
The Universe is expanding because empty space is stretching uniformly everywhere. The amount of space between us and distant galaxy directly determines how fast we perceive it to be moving away from us, which is called its "recession speed."
6.1 Density
(6.1) density = mass/volume. (SI units of density: kg/m3)
For example, the density of a material for which a cube with sides of 1 cm has a mass of 0.7 g is:
volume = 1 cm3 = 1 ⨯ 10-6 m3
density = mass/volume = 7 ⨯ 10-4 kg/(1 ⨯ 10-6 m3) = 700 kg/m3.
which is approximately the density of wood.
Since the volume of a sphere is 𝑉 = (4/3)π𝑅3 where 𝑅 is the sphere's radius, the density of a sphere of mass 𝑚 is:
(6.2) density = 𝑚/(4/3)π𝑅3.
For example, if 1 R⊙ = 6.96 ⨯ 108 m and 1 M⊙ = 1.99 ⨯ 1030 kg, the average density of the Sun is
density = 𝑚/(4/3)π𝑅3 = (1.99 ⨯ 1030 kg)/[(4/3)π(6.96 ⨯ 108 m)3] = (1.99 ⨯ 1030 kg)/[(4/3)π(3.37 ⨯ 1026 m3)]
(6.3) = 1.41 ⨯ 103 kg/m3 or about 1,400 kg/m3 or about 1.4 g/cm3.
For example, the Sun's radius is approximately 100 times that of Earth and the Sun is about 300,000 times more massive the Earth, if we compare the density of the Sun with that of Earth
(6.4) densitySun/densityEarth = (𝑚Sun/𝑚Earth)(𝑅Earth/𝑅Sun)3.4
= (300,000 𝑚Earth/𝑚Earth) (𝑅Earth/100𝑅Earth)3 = 300,000/(100)3 = 3/10 = 0.3.
This shows that the Sun's density is about one-third of the Earth"s density.
6.2 Escape speed
To understand how to move away from a planet, consider the flight of a cannonball fired from the surface of the Earth at various speeds, as shown in Figure 6.2. In this figure, 𝑉circ indicates the circular-orbit speed and 𝑉esc does the escape speed.
To calculate the value of 𝑣𝑒𝑠𝑐 at a given distance from the center of a given mass, use the equation
(6.5) 𝑣𝑒𝑠𝑐 = √(2𝐺𝑀/𝑅)
in which 𝐺 is the universal gravitational constant, 𝑀(𝑚 in the textbook) is the mass of the object from which other object is escaping, and 𝑅 is the distance between the centers of the objects. This relationship comes from an equivalence between the change in the kinetic energy (energy of motion) and the change in the gravitational potential energy (energy of position) of an object moving in a gravitational field. [Because (1/2)𝑚𝑒𝑠𝑐(𝑣𝑒𝑠𝑐)2 = 𝐺𝑚𝑒𝑠𝑐𝑀/𝑅.]
For example, the escape speed at the surface of the Earth is:
𝑣𝑒𝑠𝑐.Earth = √(2𝐺𝑀Earth/𝑅Earth) = √(2(6.67 ⨯ 10-11 m3/kg s2)(6 ⨯ 1024 kg)/(6.4 ⨯ 106 m) = √(1.25 ⨯ 108 m/s2) = 1.1 ⨯ 104 m/s or 11 km/s.
For another example, if we could crush all the mass of the Earth into a sphere half its present radius the escape speed from its new surface is:
𝑣𝑒𝑠𝑐.small-Earth/𝑣𝑒𝑠𝑐.Earth = √(2𝐺𝑀small-Earth/𝑅small-Earth) /√(2𝐺𝑀Earth/𝑅Earth) = √(2𝐺𝑀Earth/(1/2)𝑅Earth) /√(2𝐺𝑀Earth/𝑅Earth) = √2/1 ≈ 1.4
𝑣𝑒𝑠𝑐.small-Earth ≈ 1.4𝑣𝑒𝑠𝑐.Earth.
So the more compressed the mass (the higher the density and thus smaller the radius), the larger the escape speed from it. Thus, for an object of given mass, 𝑣𝑒𝑠𝑐from its surface will vary inversely as the objects's density. This relationship will be important in the definition of black holes in the following section.
6.3 Black holes
By definition, a black hole exists at any location at which the density of matter is so great that the escape speed from the vicinity of that location or exceeds the speed of light. We are to encounter black holes of several solar masses that for when the cores of massive stars collapse, or those with millions or billions of solar masses at the centers of galaxies. (The latter one is called "supermassive black holes.")
The death of a high-mass star with a mass exceeding about 8 M⊙ is an extremely violent process in which the star's outer layers are blown off in supernova explosion, leaving the extremely dense core behind.If the mass of remnant core is greater than about 3 M⊙, there's no force in the Universe that can prevent gravity from causing the material of the core to collapse into a singularity.
The event horizon is the point of no return, which is why Shep Doleman of MIT calls it "an exit door from the Universe." Nothing that approaches a black hole closer than this distance can ever escape from the gravitational force of the black hole. Even light cannot escape, which is why the object is called "black." The event horizon is a mathematically defined distance from the center of black hole. It describes an imaginary spherical surface surrounding the central singularity, not a real physical surface.
When astronomers refers to the "size" of a black hoe, they are referring to the size of Schwarzschild radius (𝑅𝑆). That radius can be determined by finding the distance at which the 𝑣𝑒𝑠𝑐 equals the speed of light. The results in the following equation:
(6.6) 𝑅𝑆 = 2𝐺𝑚/𝑐2,
where 𝑅𝑆is shorthand for Scwarzschild radius, 𝐺 is the universal gravitational constant, 𝑚 is the mass comprising the singularity, and 𝑐 is the constant speed of light.
For example, in case of the lowest-mass stellar black hole with mass of about 3 M⊙ the size of the event horizon is
𝑅𝑆 = 2𝐺(3 M⊙)/𝑐2 = [2(6.67 ⨯ 10-11 Mm2/kg2)(3(1.99 ⨯ 1030kg))]/(3 ⨯ 108m/s)2 = 8.8 ⨯ 103N ⋅ (1/kg)/(1/s2) = 8,800 m = 8.8 km.
For another example, if we consider two black holes with different mass, 3 M⊙ and 9 M⊙, the radii of their event horizons can be compared as follows
𝑅𝑆,small/𝑅𝑆,large = [2𝐺𝑚small/𝑐2]/[2𝐺𝑚large/𝑐2] = [2𝐺(3 M⊙)]/[2𝐺(9 M⊙)] = 3/9 =1/3 or 𝑅𝑆,small = 1/3 𝑅𝑆,large.
For one more example, the Schwarzschild radius for the Earth (6 ⨯ 1024 kg) is:
𝑅𝑆 = 2𝐺𝑚/𝑐2 = [2(6.67 ⨯ 10-11 Mm2/kg2)(6 ⨯ 1024kg))]/(3 ⨯ 108m/s)2 = 8.9 ⨯ 10-3 m,
which means that compressing the Earth to a tiny sphere of radius 8.9 mm would cause it to contract under its own gravity to form a black hole.
So what is the significance of the event horizon? To find out what happens at the exact distance of the event horizon from singularity, just use the expression for the Schwarzschild radius (𝑅𝑆) from Eq. 6.6 as the distance (𝑅) in Eq. 6.5:
𝑣𝑒𝑠𝑐. event horizon = √(2𝐺𝑚/𝑅𝑆) = √[2𝐺𝑚/(2𝐺𝑚/𝑐2)] = √(1/(1/𝑐2) = √𝑐2 = 𝑐.
This means that at the event horizon, 𝑣𝑒𝑠𝑐is precisely the speed of light. In fact, this is how Schwarzschild radius is defined in the first place: the distance at which escape speed equals the speed of light. Figure 6.3 shows how escape speed varies with distance from black hole.
6.4 The expansion of the Universe
This section marks a transition from individual black holes, which occupy zero volume, to cosmology, which is the study of all the matter and energy occupying the entire Universe.
One of the key discoveries in the history of cosmology is that all distant galaxies are moving away from our Milky Way galaxy, which leads to the conclusion that the Universe is expanding.There is nothing special about our perspective on this expansion: any hypothetical observer, anywhere else in the Universe, would make the same measurement, which means that there is no unique center or edge to the Universe. Space is stretching everywhere, so all galaxies are moving away from all other galaxies, provided that they are not close enough together to be gravitationally bound to one another.
The Universe is expanding because empty space is stretching uniformly everywhere. The amount of space between us and distant galaxy directly determines how fast perceive it to be moving away from us, which is called "recession speed." For example, if the distance from us to a certain galaxy is twice as far as the distance from us to another galaxy, there is twice as much expanding space between us and the more-distant galaxy, so it will appear to have twice the recession speed. Refer to Figure 6.4.
Figure 6.6 shows an example Hubble diagram with distance and recession speed of 100 hypothetical galaxies. It is clear upward linear trend in the graph. This trend is a graphical representation of Hubble's Law: more distant galaxies are receding from us more quickly. In the Hubble diagram the y-axis is recession velocity 𝑣 in km/s, x-axis is distance 𝑑 in Mpc, and the slope is called the Hubble constant or 𝐻0, pronounced "H-naught":
(6.7) 𝑣 = 𝐻0𝑑.
One approach to determine the value of 𝐻0 is to obtain it directly from the Hubble graph by calculating the slope of the line. Mathematically, sloe (𝑚) is defined as the "rise" (𝛥𝑦) divided by the "run":
(6.8) 𝑚 = 𝛥𝑦/𝛥𝑥.
For the rise and run depicted in Figure 6.6, the slope calculation is:
𝑚 = 𝛥𝑦/𝛥𝑥 = (210,000 km/s - 70,000 km/s)/(3,000 Mpc - 1,000 Mpc) = (140,000 km/s)/(2,000 Mpc) = 70 (km/s)/Mpc.
Foe example, if a Doppler-shift measurement shows that a certain galaxy is receding from us at a speed of 10,000 km/s, its distance from us is:
(6.9) 𝑑 = 𝑣/𝐻0.
= (10,000 km/s)/(70 (km/s)/Mpc) = 1,000/7 Mpc ≈ 143 Mpc or 143 ⨯ 106 pc ⨯ 3.26 ly/pc = 4.66 ⨯ 108 ly.
Since all distant galaxies are moving apart due to the explosion of the Universe, it's logical to conclude that in the pat those galaxies were all closer together. Extrapolating this expansion backward, at some time in the past all galaxies were in the same place. That is, the Universe occupied zero volume. That instant when the Universe began expanding is called the Big Bang. How long ago did that happen?
Because time = distance/speed we can use the Eq. 6.7 (𝑣 = 𝐻0𝑑)
time = distance/speed = 𝑑/𝐻0𝑑 = 1/𝐻0.
The result is an estimate of age of the age of the Universe assuming that the rate of expansion has been constant. This age often called 𝑇0 or the "Hubble time,":
(6.10) 𝑇0 = 1/𝐻0.
For example, if 𝐻0 = 70 (km/s)/Mpc, the age of the Universe or Hubble time is:
𝑇0 = 1/(70 (km/s)/Mpc) = (106 pc)/(70 km/s) = [106 pc ⨯ (3.09 ⨯ 1013 km/pc)]/(70 km/s) = (3.09 ⨯ 1019)/(70(1/s)) ≈ 4.41 ⨯ 1017 s,
or 4.41 ⨯ 1017 s (1 yr/(3.16 ⨯ 107 s) ≈ 1.4 ⨯ 1010 yr or about 14 Gyr. This is close to the widely accepted value of for the age of the Universe. [recently believed as 13.8 billion years]
Thus the Hubble time (𝑇0) is based on the assumption that the rate of expansion the Universe has not changed since the Big Bang. But since George Lemaître and Edwin Hubble discovered the expansion of the Universe in the late of 1920s, astronomer have suspected that the expansion rate is not constant. If then we should use the following equation
(6.11) 𝑑 = (1/2)𝑎𝑡2 + 𝑣0𝑡,
in which 𝑎 represent acceleration and 𝑣0 is the initial speed of the object. For several decades, many believed that the rate of expansion slowing due to the pull of gravity of all galaxies upon one another. But n the rate 1990s, astronomers made an astonishing discovery: the rate of the Universe is not slowing down, it's speeding up. The source of this positive acceleration is not fully understood (it's called "dark energy" for lack of a better term).
To understand the effect of the changing expansion rate on the age and fate of the Universe, we should first understand a "position-vs.-time" graph such as Figure 6.7. On a position-vs.-time graph
(6.12) slope = 𝛥𝑦/𝛥𝑥 = distance/time = speed
where positive slope means increasing distance. In the scenario shown in the figure, after walking away from some time, your friend turns around and walks back toward your location at the same constant speed with which she waled away.
For example, in Figure 6.8 shows your friend begins walking away from your position at a slow speed but then speeds up and walks away more quickly; after moving away at this higher speed for a short time, she slows down, come to a halt, and remains stationary as her position for the remainder of the graph.
For another example, in Figure 6.9 seems to show that shooting a cannonball toward the sky, it begins going up very quickly and gradually slows the speed until the maximum height-distance with a halt then start to return gradually faster and faster and eventually returns to the starting position with the greatest speed.
6.5 The history and fate of the Universe
Some of the most fundamental questions in cosmology relate to the evolution of the Universe. Many astronomy texts a version of cosmological position-vs.-time graph shown in Figure 6.10 which shows an annotated view. In the figure the present day to be "time zero" and place the vertical axis at that time, and the vertical axis is labeled "size" rather than position. observation can only probe the "observable Universe," which is the portion of space from which light gas had time to reach the Earth. The entire Universe may be much larger, or even infinite in extent.
Consider the points at which each of the four curves intersects the horizontal axis. For these points, the Universe occupies zero volume and therefore has infinite density. So these points represent the instant of the Big Bang. The age of an object is defined as the time that has elapsed from its birth to the present time, and this is same to the Universe. That age of Universe for four expansion scenarios is indicated by the dashed arrows in Figure 6.12.
For example, Figure 6.13 highlights the slopes for (1) and (3) scenarios. The Scenario (3) shows that the expansion rate measured at the present time is the same at all past time since the Big Bang, and at all future time. Scenario (1) shows a changing slope, which indicates a changing expansion rate. So it means the Universe was expanding very quickly at first and thr expansion rate gradually slowed after the Big Bang and is continuing to slow. Note that the Universe has always been expanding, but it has been gradually slowing.
The curves to the right of present tell us to expect in the future. For example, the right portion of scenario (1) tells us the Universe will continue to expand until the time of maximum size and it will be contracting - slowly at first then faster since the slope becomes more negative. Eventually, the Universe will return to its original size - occupying zero volume and infinitely dense. Figure 6.14 highlights he end behavior of all four scenarios. in scenario (2), the expansion of the Universe is perpetually slowing, but never quite stops. This behavior is an asymptote and the Universe approaches a maximum size as time approaches infinity. So only scenario (2) reaches a constant size. Notice that in other cases, (3) and (4), the Universe approaches an infinite size as time approaches infinity.
* Textbook: D. Fleisch & J. Kregenow A Student's Guide to the Mathematics of Astronomy (Cambridge University Press 2013) |
|
|





































