|
김관석
|
2023-06-12 13:50:03, 조회수 : 5,531 |
- Download #1 : Penrose_1965s.jpg (77.7 KB), Download : 3

GRAVITATIONAL COLLAPSE AND SPACE-TIME SINGULARITIES*
The discovery of the quasistellar radio sources has stimulated renewed interest in the question of gravitational collapse. It has been suggested by some authors1 that the enormous amounts of energy that these objects apparently emit may result from the collapse of a mass of the order of (106-108)𝛭⊙a to the neighborhood of its Schwarzschild radius, accompanied by a violent release of energy, possibly in the form of gravitational radiation. The detailed mathematical discussion of such situations is difficult since the full complexity of general relativity is required. Consequently, most exact calculations concerned with the implications of gravitational collapse have employed the simplifying assumption of spherical symmetry. Unfortunately, this precludes any detailed discussion of gravitational radiation−which requires at least a quadripole structure.
The general situation with regard to a spherically symmetrical body is well known.2 For a sufficiently great mass, there is no final equilibrium state. When sufficient thermal energy has been radiated away, the body contracts and continues to contract until a physical singularity is encountered at 𝑟 = 0. As measured by local comoving observers, the body passes within its Schwarzschild radius 𝑟 = 2𝑚. (The densities at which this happens need not be enormously high if the total mass is large enough.) To an outside observer the contraction to 𝑟 = 2𝑚 appears to take an infinite time. Nevertheless, the existence of a singularity presents a serious problem for any complete discussion of the physics of the interior region.
The question question has been raised as to whether this singularity is, in fact, simply a property of the high symmetry assumed. The matter collapses radially inwards to the single point at the center, so that a resulting spacetime catastrophe there is perhaps not surprising. Could not the presence of perturbations which destroy the spherical symmetry alter the situation drastically? The recent rotating solution of Kerr3 also possesses a physical singularity, but since a high degree of symmetry is still present (and the solution is algebraically special), it might again be argued that this is not representative of the general situation.4 4 Collapse without assumptions of symmetry5 will be discussed here.
Consider the time development of a Cauchy hypersurface 𝐶3 representing an initial matter distribution.We may assume Einstein's field equations and suitable equations of state governing the matter. In fact, the only assumption made here about these equations of state will be the non-negative definiteness of Einstein's energy expression (with or without cosmological term). Suppose this matter distribution undergoes gravitational collapse in a way which, at first, qualitatively resembles the spherically symmetrical case. It will be shown that, after a certain critical condition has been fulfilled, deviations from spherical symmetry cannot prevent space-time singularities from arising. If, as seems justifiable, actual physical singularities in space-time are not to be permitted to occur, the conclusion would appear inescapable that inside such a collapsing object at least one of the following holds: (a) Negative local energy occurs.6 (b) Einstein's equations are violated. (c) The space-time manifold is incomplete.7 (d) The concept of space-time loses its meaning at very high curvatures−possibly because of quantum phenomena.2 In fact (a), (b), (c), (d) are somewhat interrelated, the distinction being partly one of attitude of mind.
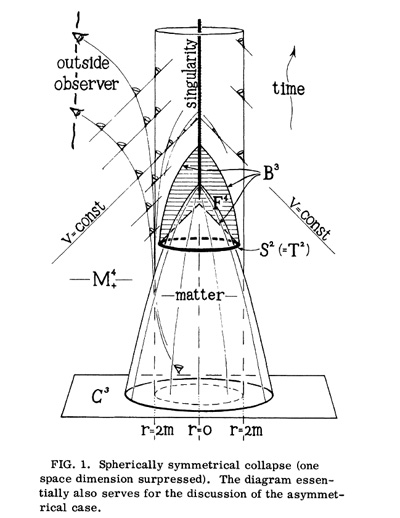
Before examining the asymmetrical case, consider a spherically symmetrical matter distribution of finite radius in 𝐶3 which collapses symmetrically. The empty region surrounding the matter will, in this case, be a Schwarzschild field, and we can conveniently use the metric 𝑑𝑠2 = -2𝑑𝑟𝑑𝜐 + 𝑑𝜐2(I - 2𝑚/𝑟) - 𝑟2(𝑑𝜃2 + sin2𝜃𝑑𝜑2), with an advanced time parameter 𝜐 to describe it.8 The situation is depicted In Fig. 1. Note that an exterior observer will always see matter outside 𝑟 = 2𝑚, the collapse through 𝑟 = 2𝑚 to the singularity at 𝑟 = 0 being invisible to him.
After the matter has contracted within 𝑟 = 2𝑚, a spacelike sphere 𝑆2 (𝑡 = const, 2𝑚 > 𝑟 = cosnt) can be found in the empty region surrounding the matter. This sphere is an example of what will be called here a trapped surface−defined generally as a closed, spacelike, two-surface 𝛵2 with the property that the two systems of null geodesics which meet 𝛵2 orthogonally converge locally in future directions at 𝛵2. Clearly trapped surface will still exist if the matter region has no sharp boundary or if spherical symmetry is dropped, provided that the derivations from the above situation are not too great. Indeed, the Kerr solutions with 𝑚 > 𝑎 (angular momentum 𝑚𝑎) all possess trapped surfaces, whereas those for which 𝑚 ≤ 𝑎 do not.9 The argument will be to show that the existence of a trapped surface implies−irrespective of symmetry−that singularities necessarily develop.
The existence of a singularity can never be inferred, however, without an assumption such as completeness for the manifold under consideration. It will be necessary, here, to suppose that the manifold 𝛭+4, which is the future time development of an initial Cauchy hypersurface 𝐶3 (past boundary of the 𝛭+4 region), is in fact null complete into the future.. The various assumptions are, more precisely, as follows: (i) 𝛭+4 is a nonsingular (+---) Riemannian manifold for which the null half-cones form two separate systems ("past" and "future"). (ii) Every null geodesic in 𝛭+4 can be extended into the future to arbitrarily large affine parameter values (null completeness). (iii) Every timelike or null geodesic in 𝛭+4 can be extended into the past until it meets 𝐶3 (Cauchy hypersurface condition). (iv) At every point of 𝛭+4, all timelike vectors 𝑡𝜇 satisfy (-𝑅𝜇𝜈 + ½𝑅𝑔𝜇𝜈 - 𝜆𝑔𝜇𝜈) 𝑡𝜇𝑡𝜈 ≥ 0 (non-negativeness of local energy). (v) There exists a trapped surface 𝛵2 in 𝛭+4. It will be shown here, in outline, that (i), ⋅⋅⋅, (v) are together inconsistent.
Let 𝐹4 be the set of points in 𝛭+4 which can be connected to 𝛵2 by a smooth timelike curve leading into the future from 𝛵2. Let 𝐵3 be the boundary of 𝐹4. Local considerations show that 𝐵3 is null where it is nonsingular, being generated by the null geodesic segments which meet 𝛵2 orthogonally at a past endpoint and have a future endpoint if this is a singularity (on a caustic or crossing region) of 𝐵3. Let 𝑙𝜇 (subject to 𝑙𝜇;𝜈𝑙𝜈 = 0), 𝜌 (=-½𝑙𝜇;𝜇), and ∣𝜎∣ {=[½𝑙(𝜇;𝜈)𝑙𝜇;𝜈 - ¼(𝑙𝜇;𝜇)2]½} be, respectively, a future-pointing tangent vector, the convergence, and the shear for these null geodesics,10 and let 𝐴 be a corresponding infinitesimal area of cross section of 𝐵3. Then [(𝐴½);𝜇𝑙𝜇];𝜈𝑙𝜈= -(𝐴½𝜌);𝜇𝑙𝜇=-𝐴½(∣𝜎∣2 + 𝛷) ≤ 0 where 𝛷 = -½𝑅𝜇𝜈𝑙𝜇𝑙𝜈 [≥0 by (iv)]. Since 𝛵2 is trapped, 𝜌 > 0 at 𝛵2, whence 𝐴 becomes zero at a finite affine distance to the future of 𝛵2 on each null geodesic. Each geodesic thus encounters a caustic. Hence 𝐵3 is compact (closed), being generated by a compact system of finite segments. We may approximate 𝐵3 arbitrarily closely by a smooth, closed, spacelike hypersurface 𝐵3✶. Let 𝐾4 denote the set of pairs (𝑃, 𝑠) with 𝑃 ⋲ 𝐵3✶ and 0 ≤ 𝑠 ≤ 1. Define a continuous map 𝜇: 𝐾4 → 𝛭+4 where, for fixed 𝑃, 𝜇{(𝑃, 𝑠)} is the past geodesic segment normal to 𝐵3✶ at 𝑃 = 𝜇{(𝑃, 1)} and meeting 𝐶3 [as it must, by (iii)] in the point 𝜇{(𝑃, 0)}. At each point 𝑄 of 𝜇{𝐾4}, we can define the degree 𝑑(𝑄) of 𝜇 to be the number of points of 𝐾4 which map to 𝑄 (correctly counted). Over any region not containing the image of a boundary point of 𝐾4, 𝑑(𝑄) will be constant. Near 𝐵3✶, 𝜇 is 1-1, so 𝑑(𝑄) =1. It follows that 𝑑(𝑄) =1 near 𝐶3 also, whence the degree of the map 𝐵3✶ → 𝐶3 induced by 𝜇 when 𝑠 = 0 must also be unity. The impossibility of this follows from the noncompactness of 𝐶3.
Full details of this and other related results will be given elsewhere.
--------------------------------------------------------
1 F. Hoyle and W. A. Fowler, Monthly Notices Roy. Astron. Soc. 125, 169 (1963); F. Hoyle, W. A. Fowler, G. R. Burbidge, and E. M. Burbidge, Astrophys. J. 139, 909 (1964); W. A. Fowler, Rev. Mod. Phys. 36, 545 (1964); Ya. B. Zel'dovich and I. D. Novikov, Dokl. Akad. Nauk SSSR 155, 1033 (1964) [translation: Soviet Phys.−Doklady 9, 246 (1964)]; I. S. Shklovskii and N. S. Kardashev, Dokl. Akad. Nauk SSSR 155, 1039 (1964) [translation: Soviet Phys. -Doklady 9, 252 (1964)]; Ya. B. Zel'dovich and M. A. Podurets, Dokl. Akad. Nauk SSSR 156, 57 (1964) [translation: Soviet Phys.−Doklady 9, 373 (1964)]. Also various articles in the Proceedings of the 1963 Dallas Conference on Gravitational Collapse (University of Chicago Press, Chicago, Illinois, 1964).
2 J. R. Oppenheimer and H. Snyder, Phys. Rev. 56, 455 (1939). See also J. A. Wheeler, in Relativity, Groups and Topology, edited by C. deWitt and B. deWitt (Gordon and Breach Publishers, Inc., New York, 1964); and reference 1.
3 R. P. Kerr, Phys. Rev. Letters 11, 237 (1963).
4 See also E. M. Lifshitz and I. M. Khalatnikov, Advan. Phys. 12, 185 (1963).
5 See also P. G. Bergmann, Phys. Rev. Letters 12, 139 (1964).
6 The negative energy of a "𝐶 field" may be invoked to avoid singularities: F. Hoyle and J. V. Narlikar, Proc. Roy. Soc. (London) A278, 465 (1964). However, it is difficult to see how even the presence of negative energy could lead to an effective "bounce" if local causality is to be maintained.
7 The "I'm all right, Jack" philosophy with regard to the singularities would be included under this heading!
8 D. Finkelstein, Phys. Rev. 110, 965 (1959).
9 The case 𝑚 < 𝑎 is interesting in that here a singularity is "visible" to an outside observer. Whether or not "visible" singularities inevitably arise under appropriate circumstances is an intriguing question not covered by the present discussion.
10 For the notation, etc., see E. Newman and R. Penrose, J. Math. Phys. 3, 566 (1962).
--------------------------------------------------------
(a) These are the supermassive black holes. Observations of the neutron star merger GW170817, which is thought to have generated a black hole shortly afterward, have refined the Tolman–Oppenheimer–Volkoff limit estimate to ~2.17𝛭⊙ (solar masses). [Wikipedia 'Black hole' and 'Tolman–Oppenheimer–Volkoff limit' (6/2023)]
* Roger Penrose, Department of Mathematics, Birkbeck College, London, England
(Received 18 December 1964). Physical Review Letters V.14, 57 (Jan. 1965)
[이 글은 로저 펜로즈의 유명한 아주 짧은 논문(1965)으로 2020년 노벨물리학상을 수상하게된 근거가 되었음; 📚: 중요 참고 문헌]
|
|
|





































