|
김관석
|
2024-03-03 09:33:54, 조회수 : 174 |
- Download #1 : Wa_Fig_1s.jpg (577.9 KB), Download : 5
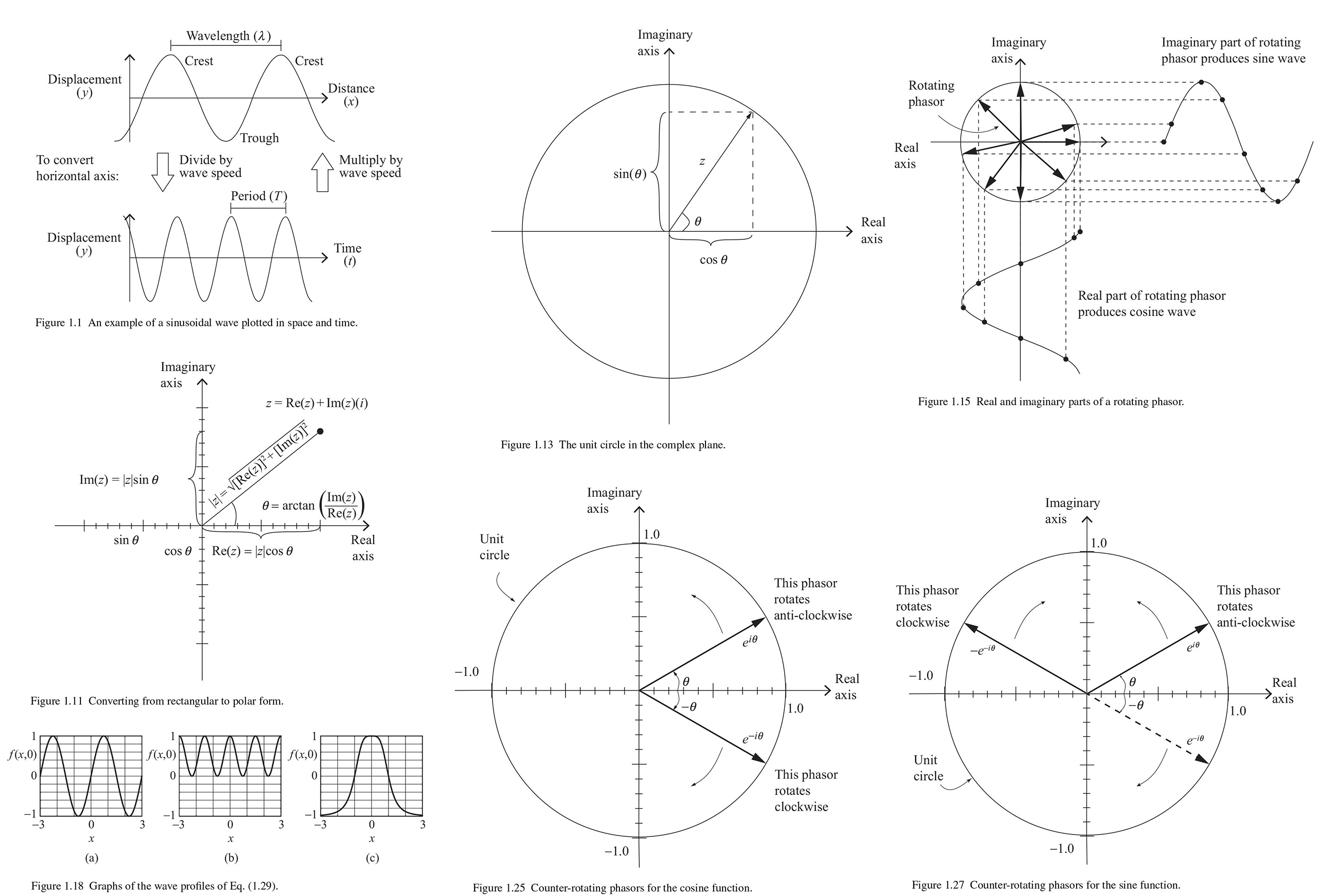

1. Wave fundamentals
1.1 Definitions
A wave is a disturbance of some kind, that is, a change from the equilibrium condition.
In propagating waves, the wave disturbance must move from place to place. But there is also non-propagating disturbances waves, such as a standing wave.
In periodic waves, the wave disturbance repeats itself in time and space. But periodic waves can be added up to a non-periodic disturbances such as a wave pulse.
Finally, in harmonic waves, the shape of wave is sinusoidal, meaning that it takes a form of a sine or cosine function. We can see plots of a sinusoidal wave in space and time in Fig. 1.1.
𝜆 ("lambda"), the wavelength: the amount of distance per cycle and the has dimension of length meters (m) in SI.
𝑇 or 𝑃, the period: the amount of time per cycle and has units of time, seconds (s) in SI.
𝑓, the frequency:the number of cycles per amount time and has units of 1 per second (1/s) in SI, also called hertz (Hz).
𝑦, the displacement: the amount of disturbance from equilibrium produced by wave and has units of distance on string, electric and magnetic field strength on electromagnetic waves, and one over the square root of length on quantum matter waves.
𝐴, the amplitude: a special value related to the displacement that occurs at the peak of a wave and has the same units as displacement. "Peak" amplitude is the maximum displacement from the equilibrium. "Peak-to-peak" amplitude is the difference between a positive peak-crest and a negative peak-trough. And "rms" amplitude is the root-mean-square value over one cycle. For sinusoidal waves, the "rms" amplitude is 1/√2(~0.707) times the peak amplitude.
𝑣, the wave speed or phase speed: How fast does a given point on a wave move? 𝑣 = 𝜆𝑓. A group speed is important for group of waves called wave packets. .
𝜙("phi"), the phase: the argument of the function that describes the wave (such as sin 𝜙) and has units of radians (rad) in SI. Its values is between 0 and ∓ 2π over one cycle.
𝜖("epsilon"):or 𝜙0, the phase constant: At the time t = 0 and location 𝑥 = 0, the phase constant 𝜖 or 𝜙0 tells us the phase of the wave.
𝜔("omega"), the angular frequency: How much angle the phase of the wave advances in a given amount of time? It has units radians per second (rad/s) in SI. 𝜔 = 2π𝑓.
𝑘, the wavenumber: How much the phase of the wave advances in a given amount of distance? It has units of radians per meter (rad/m) in SI. 𝑘 = 2π/𝜆.
1.2 Basic relationships
(1.1) 𝑓 = 1/𝑇.
(1.2) 𝜆𝑓 = 𝑣.
(1.3) 𝜔 = 2π/𝑇 = 2π𝑓.
To find the phase change (𝛥𝜙) at a certain location in a given amount of time (𝛥𝑡),
(1.4) (𝛥𝜙)constant 𝑥 = 𝜔 𝛥𝑡 = (2π/𝑇) 𝛥𝑡 = 2π (𝛥𝑡/𝑇).
(1.5) 𝑘 = 2π/𝜆.
To find the phase change (𝛥𝜙) over a given distance at a certain time,
(1.6) (𝛥𝜙)constant 𝑡 = 𝑘 𝛥𝑥 = (2π/𝜆) 𝛥𝑥 = 2π (𝛥𝑥/𝜆).
1.3.Vector concepts (omission)
1.4 Complex Numbers
The complex plane and the meaning of √-1 (typically called 𝑖 i physics) was first presented by an 18th-century Norwegian-Danish mathematician and cartographer Caspar Wessesl. We can use a complex plane with a vertical Imaginary axis and a horizontal real axis for complex number 𝑧 which consist of a "real" part and an "imaginary" part
(1.11) 𝑧 = Re(𝑧) + 𝑖[Im(𝑧)].
(1.12) ∣𝑧∣ = √[{Re(𝑧)}2 + {[Im(𝑧)]}2].
(1.13) 𝜃 = arctan [Im(𝑧)/Re(𝑧)].
For alternative method of finding the magnitude of a complex number, we can use "complex conjugate" written with a superscript with asterisk (such as 𝑧*, which is obtained by reversing the sign of the imaginary portion.
(1.14) 𝑧* = Re(𝑧) - 𝑖[Im(𝑧)].
(1.15) ∣𝑧∣ = √(𝑧*𝑧),
because ∣𝑧∣ = √𝑧*𝑧 = √[{Re(𝑧) + 𝑖{Im(𝑧)}{Re(𝑧) - 𝑖{Im(𝑧)}] = ⋅⋅⋅ = √[{Re(𝑧)}2 + {Im(𝑧)}2] in agreement with Eq. (1.12).
If we know the magnitude (∣𝑧∣) and phase (𝜃) of a complex number 𝑧, the geometry of Fig. 1.11 illustrates that the real (Re) and imaginary (Im) parts of 𝑧 may be found using
(1.16) Re(𝑧) = ∣𝑧∣cos 𝜃, Im(𝑧) = ∣𝑧∣sin 𝜃.
The polar form of a complex number is sometimes written as
Complex Number = Magnitude∠Angle or
(1.17) 𝑧 = ∣𝑧∣∠𝜃.
It's very useful to consider a special subset "unit circle" as in Fig. 1.13 which is comprised of all the points that formsa circle around the origin at a distance of exactly one unit. The real and imaginary components of any number on the unit circle (∣𝑧∣ = 1) must be
(1.18) Re(𝑧) = ∣𝑧∣cos 𝜃 = 1cos 𝜃, Im(𝑧) = ∣𝑧∣sin 𝜃 = 1sin 𝜃.
(1.19) 𝑧 = cos 𝜃 + 𝑖sin 𝜃.
One reason why phasors are extremely useful in the analysis of waves is shown in Fig. 1.15. As shown in the right portion of the figure as the phasor rotates, projection of the phasor onto the imaginary axis traces out a sine wave as 𝜃 increases. And, as shown in the bottom portion of the same figure, the projection of the phasor onto the real axis traces out a cosine wave as 𝜃 advances.
1.5 Euler relations
It would be nice to package all the information we need to define 𝑧 into an easier-to-use function of 𝜃. To fine that function, one approach is to look at the behavior of its derivatives. So we can get the first derivative and the second derivative as below
(1.20) 𝑑𝑧/𝑑𝜃 = -sin 𝜃 + 𝑖cos 𝜃 = 𝑖(cos 𝜃 + 𝑖sin 𝜃) = 𝑖𝑧,
(1.21) 𝑑2𝑧/𝑑𝜃2 = -cos 𝜃 + 𝑖cos 𝜃 = 𝑖2(cos 𝜃 + 𝑖sin 𝜃) = -𝑧.
We may solve the differential equation 𝑑𝑧/𝑑𝜃 = 𝑖𝑧 or guess a solution. Because Eq. (1.20) says change in the function 𝑧 as 𝜃 change (𝑑𝑧/𝑑𝜃) is equal to the function (𝑧) times a constant (𝑖). Another factor of 𝑖 is picked up each time a derivative with respect to 𝜃 is taken, which implies that 𝑖 is multiplied by 𝜃 within the function. So the a good guess is the function might be something to the 𝑖𝜃. The "something"- call it 𝑎 - must be a special value so that 𝑑𝑎𝑖𝜃/𝑑𝜃 brings down a factor of 𝑖 but otherwise leaves the function unchanged. We learned the number must be 𝑒.
(1.22) 𝑑𝑧/𝑑𝜃 = 𝑖(𝑒𝑖𝜃) = 𝑖𝑧.
(1.23) 𝑑2𝑧/𝑑𝜃2 = 𝑖2(𝑒𝑖𝜃) = 𝑖2𝑧.
These are the same results as we obtained in Eqs. (1.20) and (1.21) by using 𝑧 = cos 𝜃 + 𝑖sin 𝜃. So we have now the Euler relation
(1.24) 𝑒∓𝑖𝜃 = cos 𝜃 ∓ 𝑖sin 𝜃.
1.6 Wave functions
The wavefunction of any wave is the function that defines the value of the wave's disturbance at every place and time such as
(1.25-7) 𝑦(𝑥, 𝑡) = 𝑓(𝑥, 𝑡), 𝑦 = 𝑓(𝑥, 𝑡), or 𝜓 = 𝑓(𝑥, 𝑡).
Among them 𝜓("psi") is commonly used to represent wave function in quantum mechanics.
The easiest way to think about the shape of a wave is to imagine taking a snapshot of the wave at some instant of time. So we can start the snapshot of 𝑡 = 0 written as
(1.28) 𝑦 = 𝑓(𝑥, 0).
Many waves maintains the same shape over time and is called "non-dispersive" waves. For them 𝑓(𝑥, 0) can be written as 𝑓(𝑥) and the function 𝑓(𝑥) can then be called "wave profile". Some example wave profiles are as in Fig. 1.18
(1.29) 𝑦 = 𝑓(𝑥, 0) = 𝛢 sin(𝑘𝑥), 𝑦 = 𝑓(𝑥, 0) = 𝛢[cos(𝑘𝑥)]2, 𝑦 = 𝑓(𝑥, 0) = 1/(𝑎𝑥4+ 𝑏).
Then we can investigate how the functional dependence of the displacement is related to the phase of the wave. The total phase change over both space (𝛥𝜙const 𝑡 = 𝑘 𝛥𝑥) and time (𝛥𝜙const 𝑥 = 𝜔 𝛥𝑡) can be written as
(1.30) 𝛥𝜙 = 𝜙 - 𝜙0 = 𝑘 𝛥𝑥 ∓ 𝜔 𝛥𝑡.
If the starting phase 𝜙0 is taken as zero, the phase at any location (𝑥) and time (𝑡) can be written as
(1.31) 𝜙 = 𝑘𝑥 ∓ 𝜔𝑡.
Thus we have
(1.32) 𝑦(𝑥, 𝑡) = 𝑓(𝑘𝑥 ∓ 𝜔𝑡).
When we compare the sign of the additional term with that of 𝑥-term, if those signs are the same the function is shifted in the negative 𝑥-direction, and if those signs are opposite, the function is shifted in the positive 𝑥-direction.
(1.34-5) 𝑦(𝑥, 𝑡) = 𝑓(𝑘𝑥 + 𝜔𝑡), 𝑦(𝑥, 𝑡) = 𝑓(𝑘𝑥 - 𝜔𝑡).
In Eq. (1.32) we can fine the speed (𝑣), called "phase speed" of the wave, with which a given point on the wave moves.
(1.36-7) 𝑣 = 𝜆/𝛵 = (2π/𝑘)/(2π/𝜔) = 2π/𝑘 𝜔/2π, 𝑣 = 𝜔/𝑘, [meters/second] = [radians/second ⨯ meters/radian].
We may also encounter a version of Eq. (1.32) in which the wave phase speed appears explicitly.
(1.38) 𝑦(𝑥, 𝑡) = 𝑓(𝑘𝑥 ∓ 𝜔𝑡) = 𝑓(𝑘𝑥 ∓ 𝑘𝑣𝑡) = 𝑓[𝑘(𝑥 ∓ 𝑣𝑡)], or 𝑦(𝑥, 𝑡) = 𝑓(𝑥 ∓ 𝑣𝑡).
1.7 Phasor representation of wavefunctions
Putting together the concepts of the complex plane, the Euler relations, and phasors provides a very powerful tool for analysis of wavefunctions:
(1.39) 𝑦1(𝑥, 𝑡) = 𝛢1 sin(𝑘1𝑥 + 𝜔1𝑡 + 𝜖1), 𝑦2(𝑥, 𝑡) = 𝛢2 sin(𝑘2𝑥 + 𝜔2𝑡 + 𝜖2).
If the amplitudes of these waves are equal and the waves also have the same wavelength and the same frequency, then the only difference between the waves must be due to the phase constants (𝜖1 and 𝜖2). Taking 𝜖1 as zero and 𝜖2 as π/2, the wavefunctions are
(1.40) 𝑦1(𝑥, 𝑡) = 𝛢 sin(𝑘𝑥 + 𝜔𝑡), 𝑦2(𝑥, 𝑡) = 𝛢 sin(𝑘𝑥 + 𝜔𝑡 + π/2).
To plot such wavefunctions on a two-dimensional graph, we have to decide whether we wish to see how they behave as a function of distance (𝑥) or as a function of time (𝑡). At time 𝑡 = 0, the wavefunctions are
(1.41) 𝑦1(𝑥, 0) = 𝛢 sin(𝑘𝑥), 𝑦2(𝑥, 0) = 𝛢 sin(𝑘𝑥 + π/2).
When we choose to plot these waves as a function of time (𝑡), selecting 𝑥 = 0, the wavefunctions are
(1.42) 𝑦1(0, 𝑡) = 𝛢 sin(𝜔𝑡), 𝑦2(0, 𝑡) = 𝛢 sin(𝜔𝑡 + π/2).
Phasor diagram can be extremely helpful for them also. But, the phasors are to represent 𝑒𝑖𝜃, it is useful to represent the cosine and sine function by two counter rotating phasors, as illustrated in Fig. 1.25 and Fig. 1.27
(1.43) 𝑒𝑖𝜃 + 𝑒-𝑖𝜃 = (cos 𝜃 + 𝑖sin 𝜃) + (cos 𝜃 - 𝑖sin 𝜃) = 2cos 𝜃 or cos 𝜃 = (𝑒𝑖𝜃 + 𝑒-𝑖𝜃)/2.
(1.44) 𝑒𝑖𝜃 - 𝑒-𝑖𝜃 = (cos 𝜃 + 𝑖sin 𝜃) - (cos 𝜃 - sin 𝜃) = 2𝑖sin 𝜃 or sin 𝜃 = (𝑒𝑖𝜃 - 𝑒-𝑖𝜃)/2𝑖.
So the counter-rotating phasors that make up the sine and cosine functions can be considered to be one phasor with positive frequency and another with negative frequency. (Later this concept will be extremely useful for Fourier analysis.)
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015)
p.s. 'In physics, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities.'
물리학에서 한 파동은 하나 이상인 수량의 어떤 전파하는 동적인 교란-평형으로부터의 변화-이다. [Wikipedia 3/2024]
조금 늦은 감이 있지만, 슈뢰딩거 방정식을 대하기 전에 했어야 더 좋았을 파동(wave)에 관한 학습을 하면서 핵심 내용들을 정리함.
오일러의 공식, 달랑베르의 해, 경계 조건, 푸리에 이론을 비롯해서 역학파, 전자기파 및 양자파동까지의 필수 기초사항들까지 ...
(이 글은 textbook을 영어와 html로 요약-기술해가면서 학습하는 𝑒-노트이므로, 작성 중에는 많은 오타가 있을 수 있음..ㅎ) |
|
|





































