|
김관석
|
2024-03-04 17:06:11, 조회수 : 193 |
- Download #1 : Wa_Fig_2s.jpg (444.4 KB), Download : 5
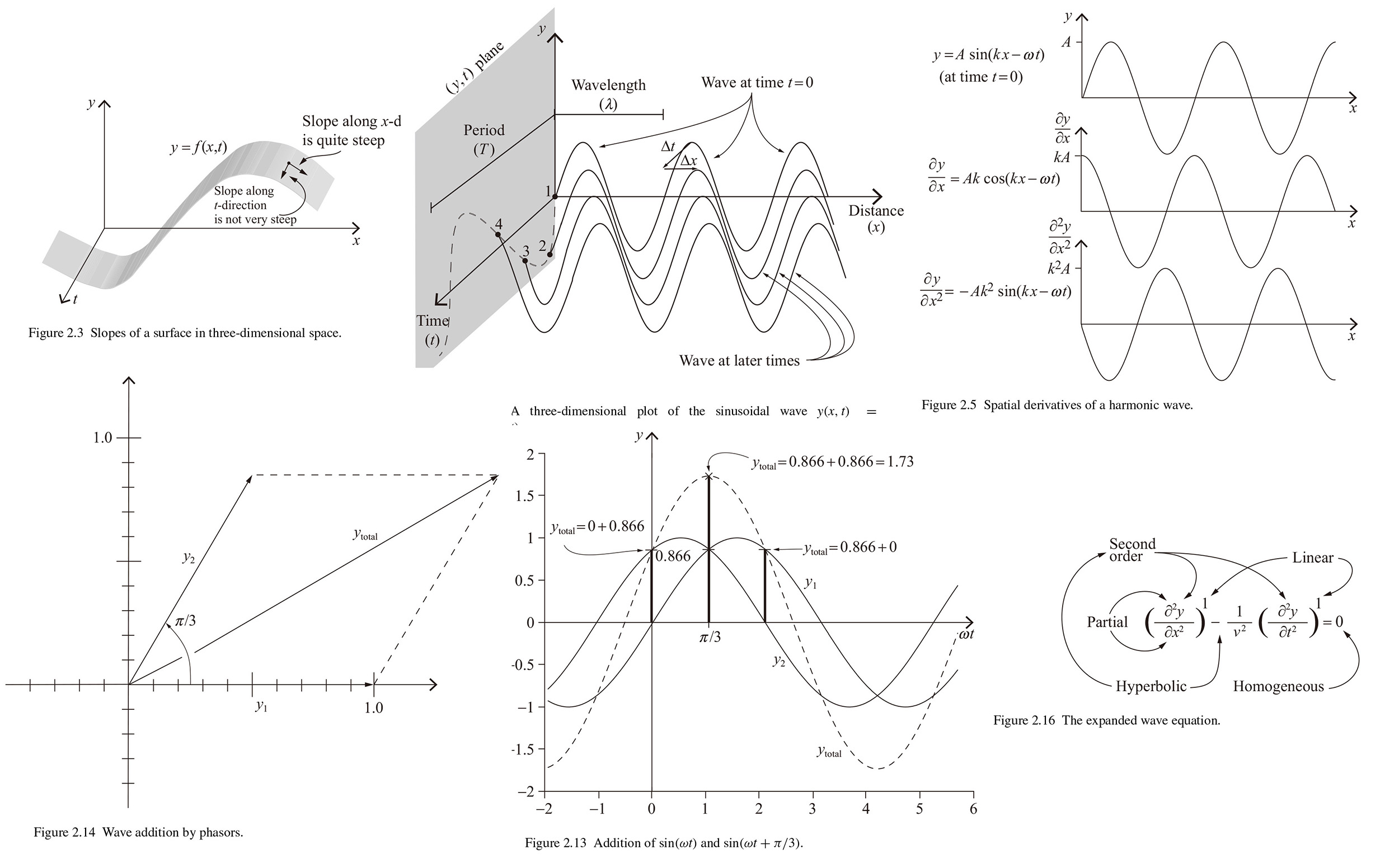

2 The wave equation
2.1 Partial derivatives
We use ordinary deriatives to find the slope of a line (𝑚 = 𝑑𝑦/𝑑𝑥) or to determine the speed of an object given its position as a function of time (𝑣𝑥 = 𝑑𝑥/𝑑𝑡). But because wavefunctions (𝑦) generally depend on two or more variables, such as distance (𝑥) and time (𝑡): 𝑦 = 𝑓(𝑥, 𝑡), we must use partial derivatives which are written as ∂/∂𝑥 or ∂/∂𝑡.
Notice that at the location shown in Fig. 2.3 the slope of the surface is quite steep in the direction of increasing 𝑥 (while remaining at the same value of 𝑡), but the slope is almost zero if you move in the direction of increasing 𝑡 (while holding our 𝑥-value constant). We can see how this works in the following example.
Example 2.1 For the function 𝑦(𝑥, 𝑡) = 3𝑥2 - 5𝑡, find the partial derivative of 𝑦 with respect to 𝑥 and with respect to 𝑡.
∂𝑦/∂𝑥 = ∂(3𝑥2 - 5𝑡)/∂𝑥 = ∂(3𝑥2)/∂𝑥 - ∂(5𝑡)/∂𝑥 = 3∂(𝑥2)/∂𝑥 - 0 = 6𝑥.
∂𝑦/∂𝑡 = ∂(3𝑥2 - 5𝑡)/∂𝑡 = ∂(3𝑥2)/∂𝑡 - ∂(5𝑡)/∂𝑡 = 0 - 5∂𝑡/∂𝑡 = -5.
We can take higher-order partial derivatives. So for example
∂/∂𝑥 (∂𝑦/∂𝑥) = ∂2𝑦/∂𝑥2 ∂/∂𝑡 (∂𝑦/∂𝑡) = ∂2𝑦/∂𝑡2.
For example, consider the wave function 𝑦(𝑥, 𝑡) = 𝐴 sin(𝑘𝑥 - 𝜔𝑡) plotted in Fig. 2.4. In this plot, we can see the behavior of 𝑦 over distance and the behavior of 𝑦 over time. And the first partial derivative of 𝑦 with respect to 𝑥 is
(2.1) ∂𝑦/∂𝑥 = ∂[𝐴 sin(𝑘𝑥 - 𝜔𝑡)]/∂𝑥 = 𝐴 ∂[sin(𝑘𝑥 - 𝜔𝑡)]/∂𝑥 = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) ∂(𝑘𝑥 - 𝜔𝑡)/∂𝑥 = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) [∂(𝑘𝑥)/∂𝑥 - (𝜔𝑡)/∂𝑥] = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) [𝑘∂𝑥/∂𝑥 - 0] or ∂(𝜔𝑡)/∂𝑥 = 𝐴𝑘 cos(𝑘𝑥 - 𝜔𝑡).
The second partial derivative of 𝑦 with respect to 𝑥 is
(2.2) ∂2𝑦/∂𝑥2 = ∂[𝐴𝑘 cos(𝑘𝑥 - 𝜔𝑡)]/∂𝑥 = 𝐴𝑘 ∂[cos(𝑘𝑥 - 𝜔𝑡)]/∂𝑥 = -𝐴𝑘 sin(𝑘𝑥 - 𝜔𝑡) ∂[(𝑘𝑥 - 𝜔𝑡)]/∂𝑥 = -𝐴 sin(𝑘𝑥 - 𝜔𝑡) [𝑘∂(𝑘𝑥)/∂𝑥 - (𝜔𝑡)/∂𝑥] = -𝐴𝑘 sin(𝑘𝑥 - 𝜔𝑡) [𝑘 ∂𝑥/∂𝑥 - 0] or ∂2𝑦/∂𝑥2 = -𝐴𝑘2 sin(𝑘𝑥 - 𝜔𝑡).
Plots of the wavefunction and its first and second partial derivatives with respect to 𝑥 at time 𝑡 = 0 are shown in Fig. 2.5. If we are wondering how the cosine shape of the first partial derivatives of 𝑦(𝑥, 𝑡) relates to the shape of the wavefunction. And turning now to the behavior of this function over time, the first partial derivative of 𝑦 with respect to 𝑡 is
(2.3) ∂𝑦/∂𝑥 = ∂[𝐴 sin(𝑘𝑥 - 𝜔𝑡)]/∂𝑡 = 𝐴 ∂[sin(𝑘𝑥 - 𝜔𝑡)]/∂𝑡 = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) ∂(𝑘𝑥 - 𝜔𝑡)/∂𝑡 = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) [∂(𝑘𝑥)/∂𝑡 - (𝜔𝑡)/∂𝑡] = 𝐴 cos(𝑘𝑥 - 𝜔𝑡) [0 - 𝜔 ∂𝑡/∂𝑡] or ∂𝑦/∂𝑡 = -𝐴𝜔 cos(𝑘𝑥 - 𝜔𝑡).
The second partial derivative of 𝑦 with respect to 𝑡 is
(2.4) ∂2𝑦/∂𝑡2 = ∂[-𝐴𝜔 cos(𝑘𝑥 - 𝜔𝑡)]/∂𝑡 = -𝐴𝜔 ∂[cos(𝑘𝑥 - 𝜔𝑡)]/∂𝑡 = 𝐴𝜔 sin(𝑘𝑥 - 𝜔𝑡) ∂(𝑘𝑥 - 𝜔𝑡)/∂𝑡 = 𝐴𝜔 sin(𝑘𝑥 - 𝜔𝑡) [∂(𝑘𝑥)/∂𝑡 - (𝜔𝑡)/∂𝑡] = 𝐴𝜔 sin(𝑘𝑥 - 𝜔𝑡) [0 - 𝜔 ∂𝑡/∂𝑡] or ∂2𝑦/∂𝑡2 = -𝐴𝜔2 sin(𝑘𝑥 - 𝜔𝑡).
2.2 The classical wave equation
The most common form of the wave equation which is often called the "classical" wave equation looks like this:
(2.5) ∂2𝑦/∂𝑥2 = 1/𝑣2 ∂2𝑦/∂𝑡2.
For example, consider 𝑦(𝑥, 𝑡) = 𝐴 sin(𝑘𝑥 - 𝜔𝑡) representing a sinusoidal wave traveling in the positive 𝑥-direction. We can start to compare the distance step to the time slope.
(2.6) 𝛥𝑥 = 𝑣 𝛥𝑡.
Then the above equation can be written as 𝛥𝑦/𝛥𝑥 = 𝑣 𝛥𝑦/𝛥𝑡 and allowing the distance and time increments to shrink toward zero. Then the 𝛥𝑠 (𝛥𝑦/𝛥𝑥 or 𝛥𝑦/𝛥𝑡) become partial derivatives, and this relationship between slopes may be written as
(2.7-8) ∂𝑦/∂𝑡 = -𝑣 ∂𝑦/∂𝑥 or ∂𝑦/∂𝑥 = -1/𝑣 ∂𝑦/∂𝑡; ∂𝑦/∂𝑡 = 𝑣 ∂𝑦/∂𝑥 or ∂𝑦/∂𝑥 = 1/𝑣 ∂𝑦/∂𝑡.
The first equation Eq. (2.6) is applied to waves moving in the positive 𝑥-direction and the next one is for the wave moving in the negative 𝑥-direction.
There is a straightforward route to solve the first- and second- order wave equation. We can start from Eq. (2.3)
Eq. (2.3): ∂𝑦/∂𝑡 = -𝐴𝜔 cos(𝑘𝑥 - 𝜔𝑡) 𝐴 cos(𝑘𝑥 - 𝜔𝑡) = -1/𝜔 ∂𝑦/∂𝑡,
and then substituting this into Eq. (2.1):
Eq. (2.1): ∂𝑦/∂𝑥 = 𝐴𝑘 cos(𝑘𝑥 - 𝜔𝑡) = -𝑘/𝜔 ∂𝑦/∂𝑡.
Using the relation 𝑣 = 𝜔/𝑘 (Eq. (1.36)) makes this
∂𝑦/∂𝑥 = -1/𝑣 ∂𝑦/∂𝑡,
which is the first-order wave equation for was propagating in the positive 𝑥-dirction.
Performing a similar analysis on the second-order equations (Eqs. (2.2) and (2.4)) yields the second the second-order classical wave equation.
Eq. (2.4): ∂2𝑦/∂𝑡2 = -𝐴𝜔2 sin(𝑘𝑥 - 𝜔𝑡) 𝐴 sin(𝑘𝑥 - 𝜔𝑡) = - 1/𝜔2 ∂2𝑦/∂𝑡2,
which we can then substitute into Eq. (2.2):
∂2𝑦/∂𝑥2 = -𝐴𝑘2 sin(𝑘𝑥 - 𝜔𝑡) = -𝑘2/𝜔2 ∂2𝑦/∂𝑡2
Again using the relation 𝑣 = 𝜔/𝑘 (Eq. (1.36)) gives
∂2𝑦/∂𝑥2 = 1/𝑣2 ∂2𝑦/∂𝑡2,
which is the classical second-order wave equation (Eq. (2.5)). Starting with the wavefunction 𝑦(𝑥, 𝑡) = 𝐴 sin(𝑘𝑥 + 𝜔𝑡) gives the same result.
We may encounter versions of the wave equation that looks quite different from the presented in this section. One common way of writing Eq. (2.2) for harmonic wave is
(2.9) ∂2𝑦/∂𝑥2 = -𝐴𝑘2 sin(𝑘𝑥 - 𝜔𝑡) = -𝑘2𝑦, or
(2.10) ∂2𝑦/∂𝑡2 = -𝐴𝜔2 sin(𝑘𝑥 - 𝜔𝑡) = -𝜔2𝑦,
since 𝑦 = 𝐴2 sin(𝑘𝑥 - 𝜔𝑡) in this case.
We may also encounter the "dot" and "double-dot" notation, in which first derivative with respect to time are signified by a dot over the variable and second derivatives with respect to time are signified by two dots over the variable. Using this notation Eq. (2.10) becomes
ÿ= -𝜔2𝑦 and ∂2𝑦/∂𝑥2 = 1/𝑣2 ÿ.
Another common notation for derivatives uses subscripts to indicate the variable with respect to which the partial derivatives is taken. For example.
∂𝑦/∂𝑥 ≡ 𝑦𝑥,
where the symbol ≡ means "is defined as". The second partial derivative with respect to 𝑡 may be written as
∂2𝑦/∂𝑡2 ≡ 𝑦𝑡𝑡,
so the classical wave equation looks like this:
𝑦𝑥𝑥 = 1/𝑣2 𝑦𝑡𝑡.
The classical wave equation can be expanded to higher dimensions by adding partial derivatives in other directions. For example, for a spatially three-dimensional wavefunction Ψ(𝑥, 𝑦, 𝑧, 𝑡), the classical wave equation is
(2.11) ∂2Ψ/∂𝑥2 + ∂2Ψ/∂𝑦2 + ∂2Ψ/∂𝑧2 = 1/𝑣2 ∂2Ψ/∂𝑡2.
We may see this written as
(2.12) 𝛻2Ψ = 1/𝑣2 ∂2Ψ/∂𝑡2,
in which the symbol 𝛻2 represents the Laplacian operator.
2.3 Properties of the wave equation
Partial. The classical wave equation is a partial differential equation (PDE), because it depends on changes in the wavefunction with respect to more than one variables (such as 𝑥 and 𝑡). The alternative is an ''ordinary'' differential operation (ODE), which depends on changes with respect to only a single variable. An example of the latter is Newton's second law, which states that the acceleration of an object is equal to the sum of the external forces on the object (∑𝐹ext) divided by the object's mass (𝑚). The one-dimensional version is
(2.13) 𝑑2𝑥/𝑑𝑡2 = ∑𝐹ext/𝑚.
We can see how the PDE works in Section 2.4 of this chapter.
Homogeneous. The classical wave equation is homogeneous because it contains only terms involve the dependent variable or derivatives of the dependent variable. Mathematically, that means the classical (homogeneous) wave equation looks like
(2.14) ∂2𝑦/∂𝑥2 - 1/𝑣2 ∂2𝑦/∂𝑡2 = 0.
as opposed to the inhomogeneous case, which looks like
(2.15) ∂2𝑦/∂𝑥2 - 1/𝑣2 ∂2𝑦/∂𝑡2 = 𝐹(𝑥, 𝑡),
where 𝐹(𝑥, 𝑡) represents some function of the independent variables 𝑥 and 𝑡 (but not 𝑦).
The external function 𝐹(𝑥, 𝑡) is called a "source" or "an "external force", and those are good clue as it meaning.Whatever they're called, The term not involving the dependent variable always represents an external stimulus of some kind. To see that, look back at Eq. (2.13).
Second-order. The classical wave equation is a second-order partial diffrrential equation. It's the change in the waveform's slope over distance that's related to the change in the slope over time are second derivatives.
Hyperbolic. We may encounter the wave equation called a "hyperbolic" differential equation. Hyperbolas are a form of conic section (along with ellipses and parabolas) that can be represented by simple equations. The classical wave equation has a similar form to the equation for a hyperbola:
(2.16) 𝑦2/𝑎2 - 𝑥2/𝑏2 = 1,
in which the constants 𝑎 and 𝑏 determine the "flatness" of the hyperbola.
To compare this with the classical wave equation (Eq. (2.5)), it helps to first get both terms onto the left side:
(2.17) ∂2𝑦/∂𝑥2 - 1/𝑣2 ∂2𝑦/∂𝑡2 = 0,
where the second derivatives as well as the negative sign between them make the wave equation "hyperbolic". If we consider the equation
(2.18) 𝑦2/𝑎2 - 𝑥2/𝑏2 = 0,
we can find that the solutions are two straight lines that cross at the origin which is a special case of a hyperbola. And, we will in the section 2.4, there are useful differential equations with a first-order time derivative and a second-order space derivative, and such equations are characterized as "parabolic".
Linear. The classical wave equation is linear because all of the terms involving the wavefunction 𝑦(𝑥, 𝑡) and derivatives of 𝑦(𝑥, 𝑡) are raised to the first power, and there are no cross terms involving the product of the wavefunction and its derivatives. If a differential equation does include terms which higher powers or cross terms of the wavefunction and its derivatives, that differential equation is said to be nonlinear.
An extremely powerful characteristic of all linear differential equations is that solutions obey the "superposition principle". Mathematically, the superposition principle says that, if two wavefunction 𝑦1(𝑥, 𝑡) and 𝑦2(𝑥, 𝑡) are each a solution to the linear equation, then their sum at every point in space and time, 𝑦total(𝑥, 𝑡) = 𝑦1(𝑥, 𝑡) + 𝑦2(𝑥, 𝑡). We can prove this for two waves traveling at the same speed 𝑣 by writing the wave equation of each wave:
(2.19) ∂2𝑦1(𝑥, 𝑡)/∂𝑥2 - 1/𝑣2 ∂2𝑦1(𝑥, 𝑡)/∂𝑡2 = 0, ∂2𝑦2(𝑥, 𝑡)/∂𝑥2 - 1/𝑣2 ∂2𝑦2(𝑥, 𝑡)/∂𝑡2 = 0,
and then adding these two equations:
∂2𝑦1(𝑥, 𝑡)/∂𝑥2 + ∂2𝑦2(𝑥, 𝑡)/∂𝑥2 - (1/𝑣2) ∂2𝑦1(𝑥, 𝑡)/∂𝑡2 - (1/𝑣2) ∂2𝑦2(𝑥, 𝑡)/∂𝑡2 = 0.
This can be simplified to
∂2[𝑦1(𝑥, 𝑡) + 𝑦2(𝑥, 𝑡)]/∂𝑥2 - 1/𝑣2 ∂2[𝑦1(𝑥, 𝑡) + 𝑦2(𝑥, 𝑡)]/∂𝑡2 = 0
and, since 𝑦total(𝑥, 𝑡) = 𝑦1(𝑥, 𝑡) + 𝑦2(𝑥, 𝑡), this is
(2.20) ∂2𝑦total(𝑥, 𝑡)/∂𝑥2 - 1/𝑣2 ∂2𝑦total(𝑥, 𝑡)/∂𝑡2 = 0.
Example 2.2 Consider two sine waves with following wavefunctions:
𝑦1(𝑥, 𝑡) = 𝐴1 sin(𝑘1𝑥 + 𝜔1𝑡 + 𝜖1),
𝑦2(𝑥, 𝑡) = 𝐴2 sin(𝑘2𝑥 + 𝜔2𝑡 + 𝜖2).
If 𝐴1 = 𝐴2 = 1, 𝑘1 = 𝑘2 = 1, 𝜔1 = 𝜔2 = 2 rad/s, but 𝜖1 = 0 and 𝜖2 = π/3, determine the characteristics of the wave that results from the addition of these waves.
(2.21) 𝑦1(𝑥, 𝑡) = 𝐴1sin(𝑘1𝑥 + 𝜔1𝑡 + 𝜖1) = sin(𝑥 + 2𝑡 + 0),
𝑦2(𝑥, 𝑡) = 𝐴2sin(𝑘2𝑥 + 𝜔2𝑡 + 𝜖2) = sin(𝑥 + 2𝑡 + π/3),
(2.22) 𝑦total(𝑥, 𝑡) = sin(𝑥 + 2𝑡) + sin(𝑥 + 2𝑡 + π/3),
(2.23) sin(𝜃1 + 𝜃2) = 2 sin[(𝜃1 + 𝜃2)/2]cos[(𝜃1 - 𝜃2)/2].
and plugging in 𝜃1 = 𝑥 + 2𝑡 and 𝜃2 = 𝑥 + 2𝑡 + π/3 gives
(2.24) 𝑦total(𝑥, 𝑡) = 2 sin[(2𝑥 + 4𝑡 + π/3)/2]cos[-(π/3)/2].
where 𝐴 = 2cos(-π/6) ≈ 1.73, and 𝑥 = 0, they look like Fig. 2.13.
Another very powerful way to analyze the superposition of waves is through the use of phasors. As shown in Fig. 2.14 for the location 𝑥 = 0 at time 𝑡 = 0, these example can be represented bu a rotating phasors. So we have
𝑦1(0, 0) = 𝐴1sin(𝑘1𝑥 + 𝜔1𝑡 + 𝜖1) = (1)sin(1(0) + 2(0) + 0) = 0,
𝑦2(𝑥, 𝑡) = 𝐴2sin(𝑘2𝑥 + 𝜔2𝑡 + 𝜖2) = (1)sin((1)(0) + 2(0) + π/3) ≈ 0.866.
If we prefer to use the "addition of components" approach to finding the resultant phasor 𝑦total, we can use the geometry of Fig. 2.14. Thus the magnitude and phase angle of 𝑦total are
(2.25-26) 𝐴total = √(1.52 + 0.8662) = 1.73, 𝜖total= tan-1 (0.866/1.5) = π/6.
Summary. All of the characteristics of the classical wave equation discussed in this section are summarized in the expanded equation shown in Fig. 2.16.
2.4 PDEs related to wave equation
There are other partial differential equations that pertain to motion through space and time, and those equations have some characteristics that are siiimilar and some that are different from the characteristics of the classical wave equation.
The advection equation. In fact, we've already seen it in Section 2.2: It's the one-way equation:
(2.27) ∂𝑦(𝑥, 𝑡)/∂𝑥 = -1/𝑣 ∂𝑦(𝑥, 𝑡)/∂𝑡.
"Advection" is a kind of transport mechanism specially describing the way substances move when they are carried along in a current. For example pollutants in a river or pollen in an air current, the advection equation can model the movement more simply than the classical wave equation.
The Korteweg-de Vries equation. Not all wave equations are linear; a well-known example of a nonlinear wave equation is the Korteweg-d Viries (KdV) equation, which describes, for example, small-amplitude, shallow, and confined water waves, called "solitary waves" or "solitons". A soliton looks like a wave pulse that retains its shape as it travels. The KdV equation has the form
(2.28) ∂𝑦(𝑥, 𝑡)/∂𝑡 - 6𝑦(𝑥, 𝑡)∂𝑦(𝑥, 𝑡)/∂𝑥 + ∂3𝑦(𝑥, 𝑡)/∂𝑥3 = 0.
The nonlinear term is the middle one, 6𝑦(∂𝑦/∂𝑥), because it includes the product of two different terms involving 𝑦(𝑥, 𝑡). The solutions no longer obey the superposition principle. However, once the solitons have passed through each other , they return to their original shapes.
The heat equation. While the classical wave equation is hyperbolic, the heat equation is parabolic, having a form analogous to 𝑦(𝑥, 𝑡) = 𝑎2. In other words, while it's still second-order in space, it's only first-order in time:
(2.29) ∂𝑦(𝑥, 𝑡)/∂𝑡 = 𝑎 ∂2𝑦(𝑥, 𝑡)/∂𝑥2,
where 𝑎 is the thermal diffusivity, a measure of how easily heat transfer through a system. The heat equation isn't classified a s a wave equation, because it is dissipative rather than oscillatory. By examining the time-dependent portion of the solution, which you can do through a common method called "separation of variables". The assumption behind this method is that, although the solution 𝑦(𝑥, 𝑡) depends on both space and time, the behavior in time 𝛵(𝑡) is independent of the behavior in space 𝑋(𝑥). That is, the wavefunction can be written as the product of 𝛵(𝑡) and 𝑋(𝑥):
(2.30) 𝑦(𝑥, 𝑡)/∂𝑡 = 𝛵(𝑡)𝑋(𝑥).
To see how that works, plug Eq. (2.30) into the heat equation:
(2.31) ∂[𝛵(𝑡)𝑋(𝑥)]/∂𝑡 = 𝑎∂2[𝛵(𝑡)𝑋(𝑥)]/∂𝑥2.
Because 𝑋(𝑥) is a constant with respect to time and 𝛵(𝑡) is independent of space. Pulling these functions out of the derivatives leavers
(2.32) 𝑋(𝑥)∂𝛵(𝑡)/∂𝑡 = 𝑎𝛵(𝑡)∂2𝑋(𝑥)/∂𝑥2.
The next step is to isolate all functions and derivatives of 𝑡 on one side and 𝑥 on the other. The heat equation now looks like
(2.33) 1/𝛵(𝑡) ∂𝛵(𝑡)/∂𝑡 = 𝑎 1/𝑋(𝑥) ∂2𝑋(𝑥)/∂𝑥2.
The left side depends only on location and does not vary with time and the right side depends only on location and does not vary with time. But if this equation is true at every location at every time, then neither side can vary at all. Thus both sides must be constant, and since the sides equal one another, they must equal the same constant. If we call that constant -𝑏, then Eq. (2.33) becomes
(2.34) 1/𝛵(𝑡) 𝑑𝛵(𝑡)/𝑑𝑡 = -𝑏,
which is an ordinary differential equation. Writing 𝛵(𝑡) as 𝛵 for simplicity and multiplying both sides by 𝑑𝑡 and integrating both sides gives
1/𝛵 𝑑𝛵 = -𝑏 𝑑𝑡 ∫ 𝑑𝛵/𝛵 = ∫ -𝑏 𝑑𝑡 or ln 𝛵 = -𝑏𝑡 + 𝑐,
in which 𝑐 is the combined integration constant for both sides. If we apply the inverse function of ln, the natural log, which is the exponential: 𝑒ln 𝑇 = 𝑇. Doing so gives
(2.35) 𝛵(𝑡) = 𝑒-𝑏𝑡+𝑐 = 𝑒-𝑏𝑡𝑒𝑐 = 𝐴𝑒-𝑏𝑡.
In this expression, the constant term 𝑒𝑐 has been absorbed into 𝐴. It's the last term (𝑒-𝑏𝑡) that make the solution dissipative.
The Scrödinger equation. The Scrödinger equation bears a stronger resemblance to the heat equation than to the classical wave equation, but its solution definitely have the characteristics of waves. Like the heat equation, the Scrödinger equation has a first-order derivative with respect to time , and a second-order derivative with respect to position. However, it has an additional factor of 𝑖 with the time derivative, and that factor has a significant impact on the nature of the solutions. We can see that by considering this form of the Scrödinger equation:
(2.36) 𝑖ℏ ∂𝑦(𝑥, 𝑡)/∂𝑡 = - ℏ2/2𝑚 ∂2𝑦(𝑥, 𝑡)/∂𝑡2 + 𝑉𝑦(𝑥, 𝑡),
where 𝑉 is the potential energy of the system and ℏ is the reduced Planck constant.
Just as with the heat equation, the time behavior of the solutions can be found by using the separation of variables. Assuming that the overall solution has the form of Eq. (2.30), the Scrödinger equation becomes
(2.37) 𝑖ℏ ∂𝛵(𝑡)𝑋(𝑥)/∂𝑡 = -ℏ2/2𝑚 ∂2𝛵(𝑡)𝑋(𝑥)/∂𝑡2 + 𝑉𝛵(𝑡)𝑋(𝑥).
Pulling 𝛵(𝑡) out of space derivatives and 𝑋(𝑥) out of the time derivatives and dividing by 𝛵(𝑡)𝑋(𝑥) gives
(2.38) 𝑖ℏ/𝛵(𝑡) ∂𝛵(𝑡)/∂𝑡 = -ℏ2/2𝑚𝑋(𝑥) ∂2𝑋(𝑥)/∂𝑡2 + 𝑉.
Using the same reasoning as described above gives a time-only equation of
(2.39) 𝑖ℏ/𝛵(𝑡) ∂𝛵(𝑡)/𝑑𝑡 = 𝐸.
This constant is the energy of the state, which is why it's called 𝐸. This is now an ordinary differential equation and can be arranged into
𝑑𝛵/𝛵 = -𝑖𝐸/ℏ 𝑑𝑡.
Now integrate each side,
ln 𝛵 = -𝑖𝐸𝑡/ℏ + 𝑐,
and solve for 𝛵(𝑡):
(2.40) 𝛵(𝑡) = 𝐴𝑒-𝑖𝐸𝑡/ℏ
Unlike the decaying exponential function 𝑒-𝑥, the real and imaginary parts of 𝑒𝑖𝑥 are oscillatory.
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015] |
|
|





































