|
김관석
|
2024-03-20 08:34:49, 조회수 : 657 |
- Download #1 : Wa_Fig_3bs.jpg (761.3 KB), Download : 0

3.3 Fourier theory
Fourier theory encompasses two related but distinct topics: Fourier synthesis and Fourier analysis. The subject of Fourier synthesis is the synthesis of a resultant waveforms by putting together the right mix of frequency components using sines and cosine, called "basic functions". Fourier analysis's goal is to "deconstruct" a given waveform into the frequency components.
One of the important principles behind Fourier theory is called "superposition", which says that the sum of any solutions to the wave equation is also a solution, So d'Alembert's general solution to the wave equation and the use of a weighted combination of sines and cosines are both examples of superposition. In the early 1800s French mathematical physicist J. B. Joseph Fourier showed that even complex functions can be produced by combining a series of harmonic functions. His theory has been applied to many various areas of science and engineering.
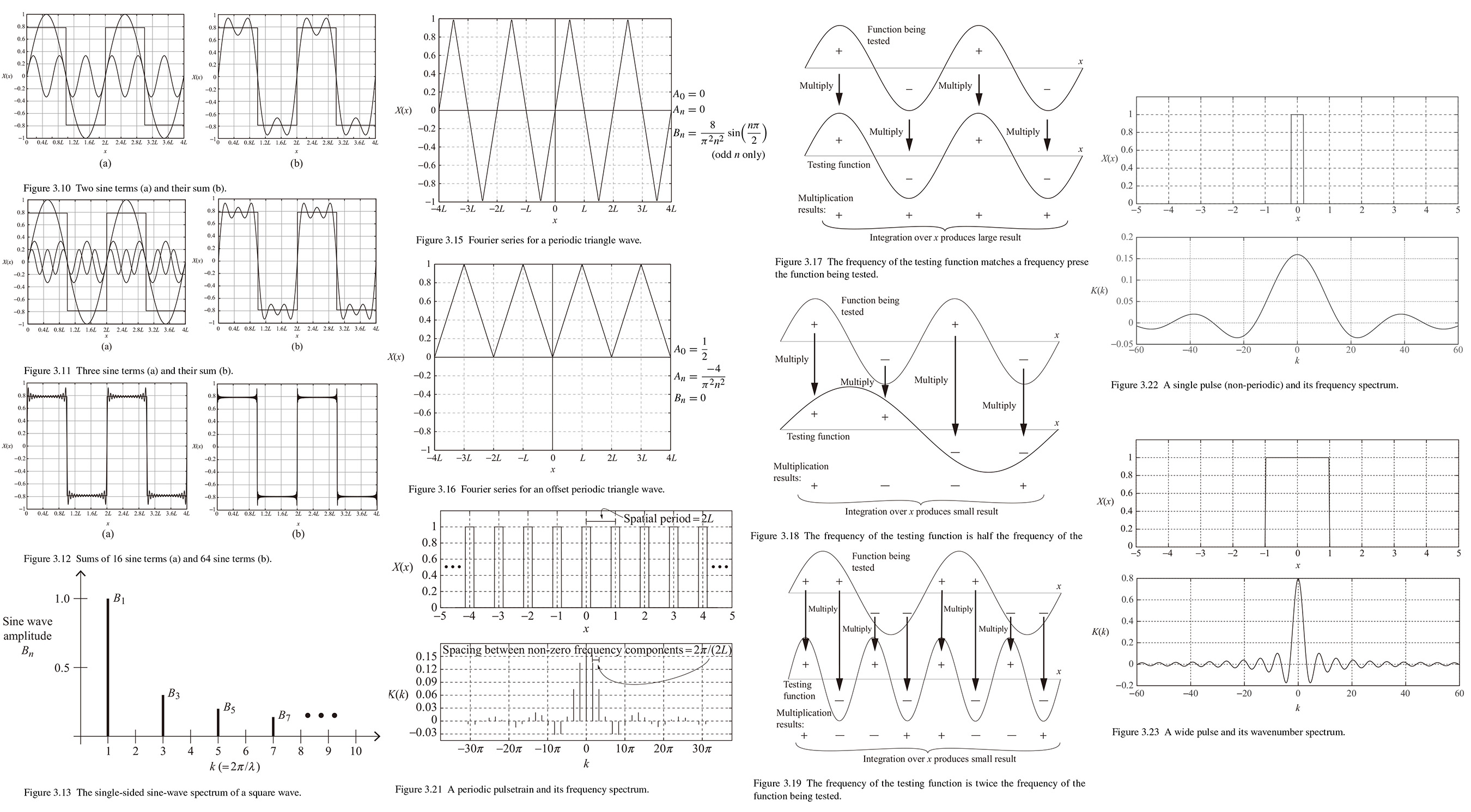
As an example, consider the square wave shown in Fig. 3.10(a). It turns out that a series waves with the right amplitudes and frequencies can be made to converge to even this very straight-edged function. The figure show what happens when we add a second sine wave with frequency that is three times higher and amplitude that is 1/3 of the fundamental. If we look at the sum of the fundamental and the second sine wave in Fig. 3.10(b), the approximation to the square wave has gotten much better, although more can be done.
If we continue to add more sine waves with the proper frequencies and amplitudes, the sum gets closer and closer to the desired square wave. In this case the frequencies must be odd integer multiples of fundamental frequency and the amplitudes must decrease by the same factor. So the terms of the series of sine waves that converge on the square wave are sin(π𝑥/𝐿), 1/3 sin(3π𝑥/𝐿), 1/5sin(5π𝑥/𝐿) and so on. We can see the result of adding 16 terms in Fig. 3.12(a) and the result of 64 terms in Fig. 3.12(b). The approximation to the square wave gets better as we add more terms.
Among the difference that will always be with us are the small overshoots and oscillations just before and after the vertical jumps in the square waves. This is called "Gibbs ripple" and it will cause an overshoot of about 9% at the discontinuities of square wave. But as in Fig. 3.12 adding more terms increase the frequency of Gibbs ripple and reduces its horizontal extent.
Instead of drawing the wave itself over space and time a bar graph showing the amplitude of each frequency component can be made. This type graph is called a "frequency spectrum". We can see an example of a wavenumber spectrum in Fig. 3.13. This figure shows the amplitude of the first for sine waves (𝐵1, 𝐵3, 𝐵5 and 𝐵7). Had we wish our square wave to oscillate between the value of +1 and -1 (rather than ∓ 0.785 as in Fig. 3.10), we could have multiplied the coefficient by a factor of 4/π ≈ 1.27.
The mathematical statement of Fourier synthesis for a spatial wavefunction with period 2𝐿 is
(3.25) 𝑋(𝑥) = 𝐴0 + ∑𝑛=1∞[𝐴𝑛 cos(𝑛2π𝑥/2𝐿) + 𝐵𝑛 sin(𝑛2π𝑥/2𝐿)],
where the 𝐴0 term represents the constant average value (also called the "DC(direct current) value).
in temporal applications, the resultant wavefunctionis made up of temporal frequency component that are periodic over time. The mathematical statement for a time function such as 𝛵(𝑡) with temporal period 𝑃 is
(3.26) 𝑇(𝑡) = 𝐴0 + ∑𝑛=1∞[𝐴𝑛 cos(𝑛2π𝑡/𝑃) + 𝐵𝑛 cos(𝑛2π𝑥/𝑃)].
in which the time period 𝑃 replaces the spatial period 2𝐿 of Eq. (3.25).
Consider again the Fourier coefficients for DC term (𝐴0), the cosine component (𝐴𝑛) and the sine component (𝐵𝑛) that result in the square wave of Fig. 3.10. Changing the values of some or all of these coefficients can drastically change the nature of the function. For example, if we modify the square-wave coefficients by making the sine coefficients decrease as 1/ 𝑛2 rather than as 1/ 𝑛 while also making every second coefficient negative, we get the waveform shown in Fig. 3.15.
The 𝐵𝑛 is shown to the right of the graph; here the sin(𝑛π/2) term causes 𝐵3, 𝐵7, 𝐵11 and so forth to be negative. The factor 8/π2 before each term causes the maximum and minimum values of the resultant wave to fall between +1 and -1.
In case of Fig. 3.16 the DC term 𝐴0 should be 1/2 and that symmetry about 𝑥 = 0 makes this an even function, cosine function (cos(- 𝑥) = cos (𝑥)). Because sine function is odd function (sin(-𝑥) = -sin(𝑥)), 𝐵𝑛 (sine) coefficients will all be zero.
The Dirichlet requirements(3) state that the Fourier series converges for any periodic function as long as that function has a finite number of extrema (maxima and minima) and a finite number of finite discontinuities in any interval.
The process of combining weighted sine and cosine components to produce a resultant waveform is called Fourier synthesis, and the process of determining which components are present in a waveform is called Fourier analysis. The key to Fourier analysis is the orthogonality of sine and cosine functions. The "orthogonality" is a generalization of the concept of perpendicularity. For example, if two functions 𝑋1(𝑥) and 𝑋2(𝑥) are orthogonal, the result of summation or integration of multiplying the value of 𝑋1(𝑥) at every value of 𝑥 by the value of 𝑋2(𝑥) at the same value of 𝑥 will be zero.
The mathematical statement of orthogonality for harmonic sine and cosine function (integer 𝑛 and 𝑚):
(3.27) 1/2𝐿 ∫-𝐿𝐿 sin (𝑛2π𝑥/2𝐿) sin (𝑚2π𝑥/2𝐿) 𝑑𝑥 = {1/2 if 𝑛 = 𝑚, 0 if 𝑛 ≠ 𝑚,
(3.28) 1/2𝐿 ∫-𝐿𝐿 cos (𝑛2π𝑥/2𝐿) cos (𝑚2π𝑥/2𝐿) 𝑑𝑥 = {1/2 if 𝑛 = 𝑚 > 0, 0 if 𝑛 ≠ 𝑚,
(3.29) 1/2𝐿 ∫-𝐿𝐿 sin (𝑛2π𝑥/2𝐿) cos (𝑚2π𝑥/2𝐿) 𝑑𝑥 = 0.
The first equation tells us that two sine wave of different frequencies (𝑛 ≠ 𝑚) are orthogonal to one another, while two sine waves of the same frequency are non-orthogonal. Likewise, the second equation says that two cosine waves of different frequencies are orthogonal, while two cosine waves of the same wave frequency are non-orthogonal. The third equation tells us that harmonic sine and cosine waves are orthooonal irrespective of whether they have the same or different frequencies.
These orthogonality relations provide the perfect tool for determining which frequency components are present in a given waveform and which are not. Imagine that we have a function that we wish to test for the presence of a certain frequency of sine wave. To conduct such a test, multiply the function we wish to test point--by-point by a "testing" sine wave and add up the results of those multiplications. If the two functions have the same frequency, the sum of those results will be a large value. This process is illustrated in Fig. 3.17..
When the frequency of the testing function does not match a frequency component being tested, the result yields small results. We can see an example in Fig. 3.18. In this case, the frequency of the testing sine wave is half the the frequency of that being tested. When we integrate across a complete cycle, the value is zero. In this case the functions are orthogonal, as we expect from q. (3.27) when 𝑛 ≠ 𝑚.
The same process works for determining whether a certain cosine wave is present in the function being tested. So we can find the Fourier 𝐴𝑛 coefficients for any function satisfying the Dirichlet requirements by multiplying that function by cosine waves and integrating the results just as we can find the Fourier 𝐵𝑛, coefficient by using the same process with sine waves. And the orthogonality of sine and cosine functions (Eq. (3.29)) guarantees that cosine components being tested will contribute to 𝐴𝑛, but will add nothing to 𝐵𝑛.
If the function being tested contains a component that has a certain frequency but offset in phase, the multiply-and-integrate process will yield a non-zero value both for 𝐴𝑛 and 𝐵𝑛. So, if the frequency component being tested is close to being in phase with the testing sine wave, the value of 𝐵𝑛 will be large and the value of 𝐴𝑛 will be small, but if the frequency component is close to being in phase with the testing cosine wave, the value of 𝐴𝑛 will be large and the value of 𝐵𝑛 will be small. This is an application of the superposition concept discussed earlier in this section and illustrated in Fig. 3.4.
Here are the mathematical statements of the process by which we can find the values of the Fourier coefficients of a waveform 𝛸(𝑥):
(3.30) 𝐴0 = 1/2𝐿 ∫-𝐿𝐿 𝛸(𝑥)𝑑𝑥,
𝐴𝑛 = 1/𝐿 ∫-𝐿𝐿 𝛸(𝑥)cos (𝑛2π𝑥/2𝐿)𝑑𝑥,
𝐵𝑛 = 1/𝐿 ∫-𝐿𝐿 𝛸(𝑥)sin (𝑛2π𝑥/2𝐿)𝑑𝑥.
Notice that to find the value of the non-oscillating component (the "DC" term) of 𝛸(𝑥) we just integrate function; the "testing function" in this case has a constant value of one and the integration yields the average value of 𝛸(𝑥).
Example 3.4. Verify the Fourier coefficients shown for the triangle wave in Fig. 3.16. Assume that 2𝐿 = 1m and the units of 𝛸(𝑥) are also meters.
First, we know 𝐵𝑛 should all be zero, since this wave an even function with non-zero average value. The equation for 𝛸(𝑥) of a straight line is 𝑦 = 𝑚𝑥 + 𝑏, where 𝑚 is the slope and 𝑏 is the 𝑦-intecept.
𝐴0 = 1/2𝐿 ∫-𝐿𝐿 𝛸(𝑥)𝑑𝑥 = 1/2(0.5) [∫-0.50 -2𝑥 𝑑𝑥 + ∫00.5 2𝑥 𝑑𝑥] = (1)[-2(𝑥2/2)∣-0.50 + 2(𝑥2/2)∣00.5] = 0 -(-0.25) + 0.25 - 0 = 0.5
and into the equation for 𝐴𝑛
𝐴𝑛 = 1/𝐿∫-𝐿𝐿 𝛸(𝑥) cos (𝑛2π𝑥/2𝐿)𝑑𝑥 = 1/0.5 [∫-0.50 -2𝑥 cos (2𝑛π𝑥/2𝐿)𝑑𝑥 + ∫00.5 2𝑥 cos (2𝑛π𝑥/2𝐿)𝑑𝑥].
Using integration by parts we can use ∫ 𝑥 cos (𝑎𝑥)𝑑𝑥 = (𝑥/𝑎)sin(𝑎𝑥) + (1/𝑎2) cos (𝑎𝑥), so 𝐴𝑛 becomes
𝐴𝑛 = (-2/0.5)[(𝑥/2𝑛π) sin (2𝑛π𝑥)∣-0.50 + (1/4𝑛2π2) cos (2𝑛π𝑥)∣-0.50] + (2/0.5)[(𝑥/2𝑛π) sin (2𝑛π𝑥)∣-0.50 + (1/4𝑛2π2) cos (2𝑛π𝑥)∣00.5]
= (-2/0.5)[0 - (-0.5/2𝑛π) sin (2𝑛π(-0.5)) + (1/4𝑛2π2) cos (2𝑛π𝑥)(1 - cos (2𝑛π(-0.5))] + (2/0.5)[(0.5/2𝑛π) sin (2𝑛π(0.5) - 0 + (1/4𝑛2π2)(cos (2𝑛π(0.5)) - 1)].
Recall that sin (𝑛π) = 0 and cos (𝑛π) = (-1)𝑛, so
𝐴𝑛 = (-2/0.5)[0 - 0 + (1/4𝑛2π2)] + (2/0.5)[0 - 0 + (1/4𝑛2π2)((-1)𝑛 - 1)]
= (-4/0.5)[1/4/𝑛2π2(1-(-1)2)] = [-2/𝑛2π2(1 - (-1)𝑛)] = -4/𝑛2π2 for odd 𝑛.
So the Fourier coefficients for the triangle wave shown in Fig. 3.16 are indeed
𝐴0 = 1/2, 𝐴𝑛 = -4/𝑛2π2 for odd 𝑛, 𝐵𝑛 = 0.
With a bit of algebraic manipulation of expanding the sine and cosine functions in Eq. (3.25) into complex exponentials using Euler relations from Chapter I, we can get to an alternative series for 𝛸(𝑥) that looks like this:
(3.31) 𝛸(𝑥) = ∑∞𝑛=-∞ 𝐶𝑛𝑒𝑖[𝑛2π𝑥/(2𝐿)].
In this equation, the coefficients 𝐶𝑛 are complex values produced by combining 𝐴𝑛 and 𝐵𝑛. Specifically, 𝐶𝑛 = 1/2 (𝐴𝑛 ∓ 𝑖𝐵𝑛), and we can find the 𝐶𝑛directly from 𝛸(𝑥) using
(3.32) 𝐶𝑛 = 1/2𝐿 ∫-𝐿𝐿 𝛸(𝑥)𝑒-𝑖[𝑛2π𝑥/(2𝐿)]𝑑𝑥.
The next major topic is the transition from discrete Fourier analysis of periodic waveforms to continuous Fourier transforms. The complex version of Fourier series makes it considerably easier to see how the equation for the Fourier transform relates to Fourier series. To understand that relationship, consider the difference between a periodic waveform and a non-periodic waveform.
Every wavenumber component of a periodic waveform must have an integer number of cycles in the interval over which the resultant waveform has one cycle. We can an example of this in wavenumber spectrum of a train of rectangular pulses shown in Fig. 3. 21. The envelope shape 𝐾(𝑘) of this spectrum is discussed below. The spatial frequency components that make up this pulsetrain must repeat themselves in the same interval as that over which the pulsetrain repeats. Most wavenumbers don't do that, so their amplitude must be zero. So if the spatial period of pulsetrain is 2𝐿, 2𝐿/2, 2𝐿/3, and so on, and since wavenumber 𝑘 = 2π/𝜆, these spatial frequency components appear at wavenumbers of 2π/2𝐿, 4π/2𝐿, 6π/2𝐿, and so on.
A single non-repeating pulse shown in Fig. 3.22. Since this waveform never repeats, its spectrum is a continuous function. Consider its period 𝛲 to be infinite, and the spacing of the frequency components is proportional to 1/𝛲. Since 1/∞ = 0, the frequency components are infinitely close together, and the spectrum is continuous. The shape of the function 𝐾(𝑘) in the figure is extremely important in physics and engineering. It's called "sine 𝑥 over 𝑥" or "sinc 𝑥" and it comes about through the continuous version of Fourier analysis called Fourier transformation.
The goal of Fourier transformation is to determine the wavenumber or frequency components of a given waveform such as 𝛸(𝑥) or 𝑇(𝑡). The mathematical statement of the Fourier transform:
(3.33) 𝐾(𝑘) = 1/√2π ∫∞𝑛=-∞ 𝛸(𝑥)𝑒-𝑖(2π𝑥/𝜆) 𝑑𝑥 = 1/√2π ∫∞𝑛=-∞ 𝛸(𝑥)𝑒-𝑖𝑘𝑥 𝑑𝑥,
where 𝐾(𝑘) represents the function of wavenumber (spatial frequency) that is the spectrum of 𝛸(𝑥). The continuous function 𝐾(𝑘) is said to exist in the "spatial frequency domain" while 𝛸(𝑥) exists in the "distance domain". The amplitude of 𝐾(𝑘) is proportional to the relative amount each spatial frequency, so 𝐾(𝑘) and 𝛸(𝑥) are said to be a Fourier transform pair. This relationship is often written as 𝛸(𝑥) ⟷ 𝐾(𝑘), and two functions related by the Fourier transform are sometimes called "conjugate variables".
If we have 𝐾(𝑘), we can use the "inverse Fourier transform" to determine 𝛸(𝑥).The inverse Fourier transform differs from the (forward) Fourier transform only by the sign of the exponent:
(3.34) 𝛸(𝑥) = 1/√2π ∫∞𝑛=-∞ 𝐾(𝑘)𝑒𝑖(2π𝑥/𝜆) 𝑑𝑘 = 1/√2π ∫∞𝑛=-∞ 𝐾(𝑘)𝑒𝑖𝑘𝑥 𝑑𝑘.
For time-domain function 𝑇(𝑡), the equivalent Fourier transformation process gives the frequency function 𝐹(𝑓):
(3.35) 𝐹(𝑓) = ∫∞𝑛=-∞ 𝑇(𝑡)𝑒-𝑖(2π𝑡/𝑇)𝑑𝑡 = ∫∞𝑛=-∞ 𝑇(𝑡)𝑒-𝑖(2π𝑓)𝑑𝑡.
Example 3.5 Find the Fourier transform of a single rectangular distance-domain pulse 𝛸(𝑥) with the height 𝐴 over interval 2𝐿 centered on 𝑥 = 0.
𝐾(𝑘) = 1/√2π ∫∞-∞ 𝛸(𝑥)𝑒-𝑖𝑘𝑥 𝑑𝑡 = 1/√2π ∫𝐿-𝐿 𝐴𝑒-𝑖𝑘𝑥 𝑑𝑡 = 1/√2π 𝐴(1/-𝑖𝑘)𝑒-𝑖𝑘𝑥∣𝐿-𝐿
= 1/√2π 𝐴 1/-𝑖𝑘 𝑒-𝑖𝑘𝐿 - 𝑒-𝑖𝑘(-𝐿)] = 1/√2π 2𝐴/𝑘[(𝑒𝑖𝑘𝐿 - 𝑒-𝑖𝑘𝐿)/2𝑖].
According to Euler equation the term in square brackets is equal to sin(𝑘𝐿) and multiplying by 𝐿/𝐿 make this
𝐾(𝑘) = (1/√2π)(2𝐴/𝑘)sin(𝑘𝐿) = [𝐴(2𝐿)/√2π][sin(𝑘𝐿)/𝑘𝐿].
This explains the sin(𝑥)/𝑥 shape of the wavenumber spectrum of the rectangular pulse shown in Fig. 3.22.
If we compare the spectrum of wide pulse with that of the narrower pulse in Fig. 3.22. we will see that the wider pulse has a narrower wavenumber spectrum 𝐾(𝑘). And the wider we make the pulse, the narrower the wavenumber spectrum becomes. That physics is called the "uncertainty principle" which is usually called "Heisenberg's uncertainty principle" in some modern physics. It describes the relationship between any function and the Fourier transform, such as 𝛸(𝑥)⟷𝐾(𝑘) or 𝑇(𝑡)⟷𝐹(𝑓).
The uncertainty principle tell us that if a function is narrow in one domain, the Fourier transform of that function cannot be narrow. And if we have a very narrow spectrum, the inverse Fourier transform gives us a function that extends over a large amount of distance or time.
The mathematical statement of the uncertainty principle between the time domain and the frequency domain is
𝛥𝑓 𝛥𝑡 = 1,
where 𝛥𝑓 represents the width of frequency-domain function and 𝛥𝑡 is the time-domain of function. The equivalent uncertainty principle for the distance/wavenumber domain is
𝛥𝑥 𝛥𝑘 = 2π,
where 𝛥𝑥 represents the width of the frequency-domain function and 𝛥𝑘 is the width of the wavenumber-domain function.
The uncertainty relations tell us that we cannot know both time and frequency with high precision. This principle will have important ramifications when it is applied to quantum waves in Chapter 6.
Although Fourier used sine and cosines as his "basic functions", it's possible to use other orthogonal functions as basis functions. Wavelets are one example of alternative basis functions.
(3) These are sometimes called the "Dirichlet conditions", but they are not the Dirichlet boundary conditions discussed in Section 3.2.
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015)
|
|
|





































