|
김관석
|
2024-04-05 19:15:54, 조회수 : 132 |
- Download #1 : Wa_Fig_4s.jpg (573.5 KB), Download : 3
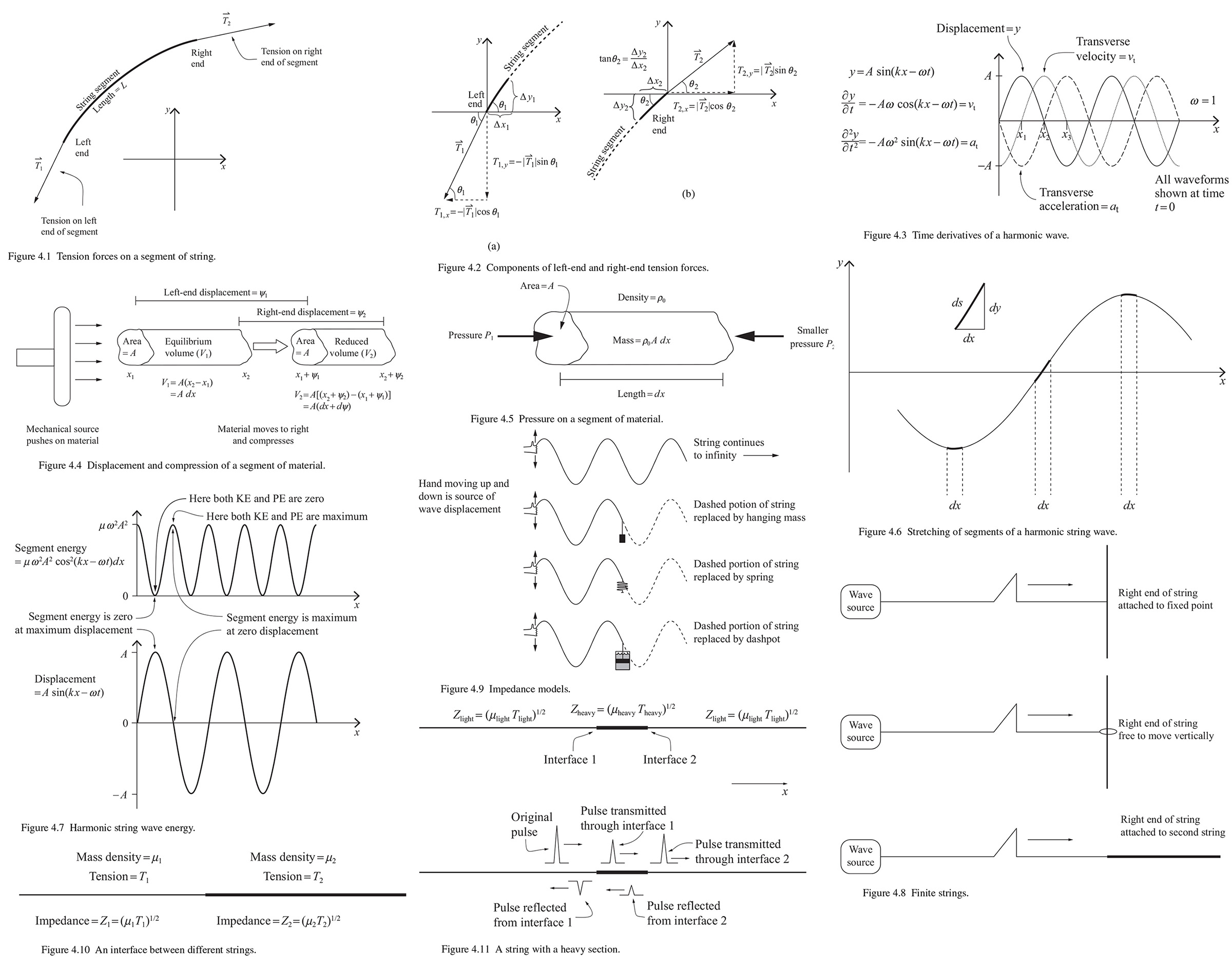

4 The mechanical wave equation
4.1 Properties of mechanical waves
For mechanical waves, the "waving" is done by bits of mass - atoms. molecules, or connected sets of particles, which means that mechanical waves can exist only within a physical material (called the "medium" in which the wave propagates). In case of a wave on a string the disturbance of the wave is the physical displacement of matter from the undisturbed (equilibrium) position and the disturbance has dimensions of distance (with SI units of meter). In pressure waves such as sound waves the disturbance may be measured as the change in the density of medium or the change in the pressure within the medium, so they are expressed a density fluctuation (with SI units of kg/m3) or a pressure change (with N/m2).
So one common aspect of all mechanical waves is that they require a physical medium. For any medium, the material's "inertial" property and its "elastic" property have a critical impact on the propagation of mechanical wave.
The inertial property of material is related mass (for discrete media) or mass density (for continuous) of the material. Because "inertia" describes the tendency of all mass to resist acceleration, material with high mass is more difficult to get moving than material with low mass. The mass density affects the velocity of propagation of material waves as well as the ability of a source to couple energy into a wave within the medium (called the "impedance" of the medium).
The elastic property of material is related to the restoring force that tends to return displaced particles to their equilibrium positions. So a medium can be elastic in the same way a rubber band or a spring is elastic - when we stretch it, displacing particles from their equilibrium positions, the medium produces restoring forces. The strength of those restoring forces joins the mass density in determining the speed of propagation, the dispersion, and the impedance of a medium.
We should understand the difference between the motion of individual particles and the motion of wave itself. For mechanical waves, the net displacement of material produced by the wave over one cycle or over million cycles, is zero. So what actually moves at the speed of the wave, as we'll see in Section 4.4, is energy.
Although the displacement of individual particles within is small, the direction of the particles' movement is important, because the direction is often used to categorize the wave as either transverse or longitudinal. In a transverse wave, the particles move in a direction that is perpendicular to the direction of wave motion. In a longitudinal wave, the particles of medium move in a direction parallel and antiparallel to the direction of wave motion. What type of wave is set up in a given medium depends on the source and on the direction of the restoring force.
4.2 Waves on a string
We can use Newton's second law to relate tension forces on a segment of a string to the acceleration of that segment. Consider a segment of a string with uniform linear density which has been displaced from the equilibrium (horizontal) position, as shown in Fig. 4.1. The string has elasticity, so as the segment is displaced, there are tension forces acting on each end, which tend to return to its equilibrium position.
As the string stretches, the mass per unit length must decrease, but we're going to consider that the change in liner density is negligible. We'll also consider vertical displacements that are small relative to the horizontal extent of the disturbance, so the angle 𝜃 that any portion of the horizontal direction is small.(1) And we'll assume the effects of all other forces (such as gravity) are negligible compared with those of the tension forces. As the segment of string is displacement from the its equilibrium position, the tension force 𝑻1 acts on the left end the tension force 𝑻2 acts on the right end. To see some interesting physics consider the the 𝑥- and 𝑦-components of the tension forces 𝑻1 and 𝑻2 shown in Fig. 4.2.
𝑇1.𝑥 = -∣𝑻1∣ cos 𝜃1, 𝑇1.𝑦 = -∣𝑻1∣ sin 𝜃1, 𝑇2.𝑥 = ∣𝑻2∣ cos 𝜃2, 𝑇2.𝑦 = ∣𝑻2∣ sin 𝜃2.
The next step is to use Newton's second law,
(4.1-2) ∑𝐹𝑥 = -∣𝑻1∣ cos 𝜃1 + ∣𝑻2∣ cos 𝜃2 = 𝑚𝑎𝑥, ∑𝐹𝑦 = -∣𝑻1∣ sin 𝜃1 + ∣𝑻2∣ sin 𝜃2 = 𝑚𝑎𝑦.
As long as the string segment oscillates up and down along the 𝑦-direction, we can take 𝑎𝑥 = 0, and if the amplitude of the oscillation is small, then 𝜃1 and 𝜃2 are both small and using approximations and setting 𝑎𝑥 to zero gives
cos 𝜃1 ≈ cos 𝜃2 ≈ 1, ∑𝐹𝑥 = -∣𝑻1∣ cos 𝜃1 + ∣𝑻2∣ cos 𝜃2 = 0, which means that
(4.3) ∣𝑻1∣ ≈ ∣𝑻2∣,
so the magnitudes of the tension forces are approximately equal, but the directions of those forces are not equal. as shown
Left-end slope = tan 𝜃1 = 𝛥𝑦1/𝛥𝑥1, Right-end slope = tan 𝜃2 = 𝛥𝑦2/𝛥𝑥2.
Consider only an infinitesimal piece of the string by letting 𝛥𝑥1 or 𝛥𝑥2 approach zero:
𝛥𝑦1/𝛥𝑥1 → [∂𝑦/∂𝑥]left, 𝛥𝑦2/𝛥𝑥2 → [∂𝑦/∂𝑥]right
Eqs. (4.4) says that the slopes of the ends of the segment are equal to the tangent of 𝜃1 and 𝜃2, for small angles those tangents may be approximated by sines:
tan 𝜃1 = sin 𝜃1/cos 𝜃1 ≈ sin 𝜃1, tan 𝜃2 = sin 𝜃2/cos 𝜃2 ≈ sin 𝜃2. Thus
∑𝐹𝑦 = -∣𝑻1∣[∂𝑦/∂𝑥]left + ∣𝑻2∣[∂𝑦/∂𝑥]right = 𝑚𝑎𝑦 and since 𝑎𝑦 = ∂2𝑦/∂𝑡2
𝑚 ∂2𝑦/∂𝑡2 = -∣𝑻1∣[∂𝑦/∂𝑥]left + ∣𝑻2∣[∂𝑦/∂𝑥]right since ∣𝑻1∣ = ∣𝑻2∣ = 𝑇:
∂2𝑦/∂𝑡2 = 𝑇/𝑚 {[∂𝑦/∂𝑥]right - [∂𝑦/∂𝑥]left} = 𝑇/𝑚 𝛥(∂𝑦/∂𝑥) which means
∂2𝑦/∂𝑡2 = 𝑇/𝑚 𝛥(∂𝑦/∂𝑥) = 𝑇/𝜇𝛥𝑥 𝛥(∂𝑦/∂𝑥), But, or small 𝛥𝑥,
𝛥(∂𝑦/∂𝑥)/𝛥𝑥 = ∂2𝑦/∂𝑥2
which means
∂2𝑦/∂𝑡2 = 𝑇/𝜇 (∂2𝑦/∂𝑥2) or
(4.5) ∂2𝑦/∂𝑥2 = 𝜇/𝑇 (∂2𝑦/∂𝑡2).
One interesting observation about this form of wave equation is that since the displacement (𝑦) in this is actually a physical displacement,(2) We can determine the phase speed of wave comparing the multiplicative term in Eq. (2.5) with that in Eq. (4.5).
1/𝑣2 = 𝜇/𝑇, so
(4.6) 𝑣 = √(𝑇/𝜇).
As expected, the phase speed of the string wave depends both on the elastic (𝑇) and on the inertial (𝜇) properties of the string (which is the medium of propagation in this case). The phase speed of the waves was simply called "𝑣", but now we know that speed to be 𝑣 = √(𝑇/𝜇).
Example 4.1 Compare the displacement velocity, and acceleration for a transverse harmonic wave on a string.
If the displacement 𝑦(𝑥, 𝑡) = 𝐴 sin(𝑘𝑥 - 𝜔𝑡), the transverse velocity 𝑣1 = ∂𝑦/∂𝑡 = -𝐴𝜔 cos(𝑘𝑥 - 𝜔𝑡), and the transverse acceleration is 𝑎𝑡 = ∂2𝑦/∂𝑡2 = -𝐴𝜔2 sin(𝑘𝑥 - 𝜔𝑡) as in Fig. 4.3.
One additional concept is the effect of changes in the linear mass density (𝜇) or tension (𝑇) of the string. We can see the effect of allowing the string characteristics to change with distance by treating both the density and tension as functions of 𝑥: 𝜇 = 𝜇(𝑥) and 𝑇(𝑥), So this modified version of the wave equation:
∂2𝑦/∂𝑡2 = 1/𝜇(𝑥) ∂/∂𝑥 [𝑇(𝑥) ∂𝑦/∂𝑥].
Notice that 𝑇(𝑥) cannot be moved out of spatial derivative, and the ratio of tension to the density may no longer constant. In general, the spatial portions of the solution to this equation are non-sinusoidal. This has an interesting analogy with quantum waves in inhomogeneous medium.
4.3 Pressure waves
By "pressure wave" we mean any wave in a medium a mechanical source causes a physical displacement and compression or refraction of the material in the direction in which the wave is propagating. We can see an illustration of how a pressure wave works in Fig. 4.4. The "disturbance" of such waves involves three things: the longitudinal displacement of material, changes in density of the material, and variation of the pressure within material. So pressure waves could also be called "density waves" or even "longitudinal displacement waves".
Though we're considering one-dimensional wave motion, pressure waves exist in a three-dimensional medium, so instead of considering the linear mass density 𝜇, it's the volumetric mass density 𝜌 that will provide the inertial characteristic of the medium. In this case, we'll assume that the pressure and density variations are small relative to the equilibrium values and consider only longitudinal displacement.
We can start by defining the pressure (𝛲) at any location in terms of the equilibrium pressure (𝛲0) and density (𝜌) at any location can be written in terms of the equilibrium density (𝜌0) and the incremental change in pressure or density produced by the wave (𝑑𝛲 or 𝑑𝜌):
𝛲 = 𝛲0 + 𝑑𝛲, and 𝜌 = 𝜌0 + 𝑑𝜌.
Before relating these quantities to he acceleration of material in the medium using Newton's second law, we had better to familiarize ourselves with the terminology and equations of volume compressibility. The compressibility of a substance is the inverse of its "bulk modulus", which relates an incremental change in pressure (𝑑𝛲) to the fractional change in density (𝑑𝜌/𝜌0) of the material:
(4.7-8) 𝐾 ≡ 𝑑𝛲/(𝑑𝜌/𝜌0) or 𝑑𝛲 = 𝐾(𝑑𝜌/𝜌0).
With this relationship in hand, we can consider Newton's second law for the segment of material being displaced and compressed or rarefied by the wave. So consider the pressure from the surrounding material acting on the left and the right side of the segment, as shown in Fig. 4.5. Setting the sum of the 𝑥-direction forces equal to the acceleration in the 𝑥-direction gives
(4.9) ∑𝐹𝑥 = 𝛲1𝐴 - 𝛲2𝐴 = 𝑚𝑎𝑥,
where 𝑚 is the mass of segment.
𝑚 = 𝜌0𝐴 𝑑𝑥.
Using the symbol 𝜓 to represent the displacement of the material due to the wave, the acceleration of the 𝑥-direction can be written as
𝑎𝑥 = ∂2𝜓/∂𝑡2.
Substituting these expressions for 𝑚 and 𝑎𝑥 into Newton's second law (Eq. (4.9)) gives
∑𝐹𝑥 = 𝛲1𝐴 - 𝛲2𝐴 = 𝜌0𝐴 𝑑𝑥 ∂2𝜓/∂𝑡2.
𝛲1𝐴 - 𝛲2𝐴 = (𝛲0 + 𝑑𝛲1)𝐴 - (𝛲0 + 𝑑𝛲2)𝐴 = (𝑑𝛲1 - 𝑑𝛲2)𝐴.
Change in overpressure = 𝑑𝛲2 - 𝑑𝛲1 = ∂(𝑑𝛲)/∂𝑥 𝑑𝑥,
which means
-∂(𝑑𝛲)/∂𝑥 𝑑𝑥 𝐴 = 𝜌0𝐴 𝑑𝑥 ∂2𝜓/∂𝑡2 or 𝜌0 ∂2𝜓/∂𝑡2 = -∂(𝑑𝛲)/∂𝑥.
But 𝑑𝛲 = 𝑑𝜌𝐾/𝜌0 (Eq. (4.8)), so
(4.10) 𝜌0 ∂2𝜓/∂𝑡2 = -∂[(𝐾/𝜌0)𝑑𝜌]/∂𝑥.
The next step is to relate the change in density (𝑑𝜌) to the displacements of the left and right ends of the segment (𝜓1 and 𝜓2). To do that, the mass of the segment is the same before and after the segment is compressed. Because 𝑚 = 𝜌𝑉, 𝑉1 = 𝐴 𝑑𝑥 before compression and 𝑉2 = 𝐴(𝑑𝑥 + 𝑑𝜓) after compression as in Fig. 4.4. Thus,
𝜌0𝑉1 = (𝜌0 + 𝑑𝜌)𝑉2, 𝜌0(𝐴 𝑑𝑥) = (𝜌0 + 𝑑𝜌)𝐴(𝑑𝑥 + 𝑑𝜓).
The change in displacement (𝑑𝜓) over distance 𝑑𝑥 can be written as
𝑑𝜓 = ∂𝜓/∂𝑥 𝑑𝑥, so
𝜌0(𝐴 𝑑𝑥) = (𝜌0 + 𝑑𝜌)𝐴(𝑑𝑥 + ∂𝜓/∂𝑥 𝑑𝑥], 𝜌0 = (𝜌0 + 𝑑𝜌) (1 + ∂𝜓/∂𝑥) = 𝜌0 + 𝑑𝜌 + 𝜌0 ∂𝜓/∂𝑥 + 𝑑𝜌 ∂𝜓/∂𝑥.
Since the last term is small relative to 𝜌0, a reasonable approximation we can write
𝑑𝜌 ≃ -𝜌0 ∂𝜓/∂𝑥.
which we can insert into Eq. (4.10), giving
𝜌0 ∂2𝜓/∂𝑡2 = -∂[(𝐾/𝜌0)(-𝜌0 ∂𝜓/∂𝑥)]/∂𝑥 = ∂[(𝐾(∂𝜓/∂𝑥)]/∂𝑥.
Rearranging makes this into an equation with a familiar form:
(4.11) 𝜌0 ∂2𝜓/∂𝑡2 = 𝐾 ∂2𝜓/∂𝑥2 or ∂2𝜓/∂𝑥2 = 𝜌0/𝐾 ∂2𝜓/∂𝑡2.
By comparing the classical wave equation Eq. (2.5) with that in Eq.(4.11). Setting these factors equal to one another gives
(4.12) 1/𝑣2 = 𝜌0/𝐾 so 𝑣 = √(𝐾/𝜌0).
So the phase speed of the pressure wave depends on the elastic, that is, the bulk modulus (𝐾) and the inertial density (𝜌0) of the medium.
Example 4.2 Determine the speed of sound in air.
Sound is a type of pressure wave, so we can use Eq. (4.12) to determine the speed of sound in air.
(4.13) 𝑣 = √(𝐾/𝜌0) = √[𝑑𝛲/(𝑑𝜌/𝜌0)/𝜌0] = √(𝑑𝛲/𝑑𝜌).
The quantity 𝑑𝛲/𝑑𝜌 can be related to equilibrium pressure (𝛲0) and density (𝜌0) using the adiabatic gas law. The adiabatic law means that we're assuming that the regions of compression and rarefaction produced by the sound wave will not lose or gain energy by heating as the wave oscillates. That's a good assumption for sound waves in air under typical condition, because the flow of energy by conduction (molecules colliding and transferring kinetic energy) occurs over distances comparable to the mean free path. (the average distance molecules travel between collisions). That distance is several orders of magnitude smaller than the distance between regions of compression of compression and rarefaction (that is, half a wavelength) in sound waves. Thus the wave action may indeed be considered to be an adiabatic process.
To apply the adiabatic gas law, we can write the relationship between pressure (𝛲) and volume (𝑉) as
(4.14) 𝛲𝑉𝛾 = constant,
in which 𝛾 represents the ratio of specific heats as constant pressure and constant volume and the approximately value is 1.4 for air under typical condition. Since volume is inversely proportional to density 𝜌, Eq. (4.14) can be written as
𝛲 = (constant)𝜌𝛾 so 𝑑𝛲/𝑑𝜌 = (constant)𝛾𝜌𝛾-1 = 𝛾 (constant)𝜌𝛾/𝜌 = 𝛾 𝛲/𝜌.
Inserting this into Eq. (4.13) gives
𝑣 = √(𝛾 𝛲/𝜌)
For typical values for air of 𝛲 = 1 ⨯ 105 Pa and 𝜌 = 1.2 kg/m3, this yields
𝑣 = √[1.4 1 ⨯ 105/1.2] = 342 m/s.
which is very close to the measured value (according to wikipedia, 343 m/s at 20 ∘C).
4.4 Energy and power of mechanical waves
What is propagating in a mechanical wave is "energy". The mechanical energy of a system consists of kinetic energy (as "energy of motion") and potential energy (as "energy of position"). The kinetic energy of a moving object is proportional to the mass of the object and the square of the object's speed, while the object's potential energy on its position in a region in which external forces act upon the object.
Potential energy comes in several types such as gravitational energy in a gravitational field and elastic potential energy by an elastic force. As we may recall, a conservative force is a force for which the work done by the force as the object changes depends only on the change in position and not on the path taken by the object. Gravity and elastic forces are conservative, while forces such a friction and drag are non-conservative, because for such dissipative forces, longer paths convert more mechanical energy into internal energy, and we don't get that energy back by getting over the same path in the opposite direction. It's only the change in the potential energy that has any physical significance.
Applying the concepts of kinetic and potential energy to a mechanical wave such as a transverse wave on a string is straightforward. The most common approach is to find expressions for the kinetic and potential energies of one small segment of the string, which give the density (that is, the energy per unit length). For harmonic waves, the kinetic energy (𝐾𝐸) of a small segment of the string depends on the segment's mass (𝑚) and the square of the segment's transverse velocity (𝑣𝑡):
𝐾𝐸segment = 1/2 𝑚𝑣𝑡2.
With a linear mass density of 𝜇 and a length of 𝑑𝑥 is 𝑚 = 𝜇𝑑𝑥, so
𝐾𝐸segment = 1/2 (𝜇 𝑑𝑥)𝑣𝑡2.
The transverse velocity of the segment is 𝑣𝑡 = ∂𝑦/∂𝑡, so
(4.15) 𝐾𝐸segment = 1/2 (𝜇 𝑑𝑥) (∂𝑦/∂𝑡)2.
In Fig. 4.3 we can expect the kinetic energy is greatest for those segment passing through the equilibrium position. And to determine the potential energy of segment, it's essential that we keep track of the stretching of the string as the segment, because the potential energy is related to the work done by the tension forces that cause the segment to stretch. A sketch of the situation is shown in Fig. 4.6 and we can approximate the segment of length (𝑑𝑠) as 𝑑𝑠 = √(𝑑𝑥2 + 𝑑𝑦2).
If we let 𝑑𝑥 approach zero, 𝑑𝑦 can be written as
𝑑𝑦 = ∂𝑦/∂𝑥 𝑑𝑥, 𝑑𝑠 = √[𝑑𝑥2 + (∂𝑦/∂𝑥 𝑑𝑥)2] = 𝑑𝑥√[1 + (∂𝑦/∂𝑥)2].
This expression can be simplified using the binomial theorem, which says that (1 + 𝑥)𝑛 ≈ 1 + 𝑛𝑥
as long as 𝑥 is small relative to one. So we can write
𝑑𝑠 = 𝑑𝑥[1 + (∂𝑦/∂𝑥)2]1/2 ≈ 𝑑𝑥[1 + 1/2 (∂𝑦/∂𝑥)2] ≈ 𝑑𝑥 + 1/2 (∂𝑦/∂𝑥)2 𝑑𝑥.
This means that the segment is stretched by an amount 𝑑𝑠 - 𝑑𝑥, which is
Amount of stretch = 𝑑𝑠 - 𝑑𝑥 = 1/2 (∂𝑦/∂𝑥)2 𝑑𝑥.
To find out the work done by elastic (tension) force in stretching the string, we can utilize the fact that the work equals the component of the force multiplied by the amount of stretch. In this case the elastic force is the tension (𝑇) of the spring, so the work is
Work = 𝑇[1/2 (∂𝑦/∂𝑥)2 𝑑𝑥].
This work is the change in potential energy (𝑃𝐸) of the segment, so the potential energy of segment:
(4.16) 𝑃𝐸segment = 𝑇[1/2 (∂𝑦/∂𝑥)2 𝑑𝑥].
The total mechanical energy (𝑀𝐸) of any segment of the string is the sum of the segment's kinetic and potential energies, which is
𝑀𝐸segment = 1/2 (𝜇 𝑑𝑥) (∂𝑦/∂𝑡)2 + 𝑇[1/2 (∂𝑦/∂𝑥)2 𝑑𝑥].
So the mechanical energy density (the energy per unit length) can be found by dividing the expression by 𝑑𝑥:
(4.17) 𝑀𝐸unit length = 1/2 𝜇 (∂𝑦/∂𝑡)2 + 𝑇[1/2 (∂𝑦/∂𝑥)2].
For wavefunction 𝑦(𝑥, 𝑡) = 𝑓(𝑥 - 𝑣phase𝑡) travelling in the positive direction, as Eq. (2.7)
(4.18) ∂𝑦/∂𝑥 = -1/𝑣phase ∂𝑦/∂𝑡, so
𝑀𝐸unit length = 1/2 𝜇 (∂𝑦/∂𝑡)2 + 𝑇[1/2 (-1/𝑣phase ∂𝑦/∂𝑡)2] = 1/2 (𝜇 + 𝑇/𝑣phase2) (∂𝑦/∂𝑡)2.
But by Eq. (4.6) 𝑣phase = √(𝑇/𝜇) which means 𝜇 = 𝑇/𝑣phase2, the above equation gives
𝑀𝐸unit length = 1/2 (𝑇/𝑣phase2 + 𝑇/𝑣phase2) (∂𝑦/∂𝑡)2 = (𝑇/𝑣phase2) (∂𝑦/∂𝑡)2.
Then ∂𝑦/∂𝑡 is the transverse speed 𝑣1, and we have
(4.19) 𝑀𝐸unit length = (𝑇/𝑣phase2) 𝑣12.
Example 4.3 What are the kinetic, potential, and mechanical energy of a segment of string of length 𝑑𝑥 with wavefunction 𝑦(𝑥, 𝑡) = 𝛢 sin(𝑘𝑥 - 𝜔𝑡)?
Transverse velocity 𝑣1 = ∂𝑦/∂𝑡 = -𝛢𝜔 cos(𝑘𝑥 - 𝜔𝑡) and the slope of wavefunction ∂𝑦/∂𝑡 = 𝛢𝑘 cos(𝑘𝑥 - 𝜔𝑡), so by Eqs. (4.15) and (4.16)
(4.20) 𝐾𝐸segment = 1/2 (𝜇 𝑑𝑥) (∂𝑦/∂𝑡)2 = 1/2 𝜇𝛢2𝜔2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥
𝑃𝐸segment = 𝑇[1/2 (∂𝑦/∂𝑥)2 𝑑𝑥] = 𝑇[1/2 𝛢2𝑘2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥].
Because 𝑣phase = √(𝑇/𝜇) and 𝑣phase = 𝜔/𝑘, 𝑇 = 𝜇𝜔2/𝑘2. Thus
𝑃𝐸segment = (𝜇 𝜔2/𝑘2) 1/2 𝛢2𝑘2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥 or
(4.21) 𝑃𝐸segment = 1/2 𝜇𝛢2𝜔2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥.
If we compare Eqs. (4.21) with (4.20), the segment's kinetic and potential energies are identical. So the total energy density:
(4.22) 𝑀𝐸segment = 𝜇𝛢2𝜔2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥.
In case of a transverse wave on a string it's the length of a segment relative to the equilibrium length. The stretched length depend on the slope (∂𝑦/∂𝑥) of he segment as in Fig. 4.6. We can see the total energy of the string segments as a function of 𝑥 in Fig. 4.7. In case of a transverse string wave, the segments's kinetic and potential energy both reach their maximum value at the same time when the segment passes through equilibrium position. To find energy in an entire wavelength of the wave, we can integrate Eq. (4.22) over a distance of one wavelength (𝜆):
𝑀𝐸one wavelength = ∫0𝜆 𝜇𝛢2𝜔2 cos2(𝑘𝑥 - 𝜔𝑡)𝑑𝑥,
which can be done by selecting a fixed time such as 𝑡 = 0 and using the definite integral
∫0𝜆 cos2[2π/𝜆 𝑥]𝑑𝑥 = 𝜆/2.
Thus the mechanical energy in each wavelength of a transverse string wave is
𝑀𝐸one wavelength = 1/2 𝜇𝛢2𝜔2𝜆.
Notice that the mechanical energy is proportional to he square of the maximum displacement (𝛢). In case of a pressure wave the energy is proportional to the square of the maximum overpressure of the wave.
Now we can find the power of the wave. Power is defined as the rate of change of energy and has SI units of joules per second or watts, and power of a propagating wave tells us the amount of energy that passes a given location per unit time. Since the product of 𝑀𝐸unit wavelength is the number of joules in the wave per meter of distance and the phase speed (𝑣phase) is the number of meters the the wave moves per second gives the power of the wave:
𝑃 = (𝑀𝐸unit wavelength)𝑣phase.
The mechanical energy density is given in Eq. (4.19), so
𝑃 = [(𝑇/𝑣phase2) 𝑣𝑡2] 𝑣phase = (𝑇/𝑣phase) 𝑣12.
Since 𝑣phase = √(𝑇/𝜇),
𝑃 = [𝑇/√(𝑇/𝜇)] 𝑣𝑡2 or
(4.23) 𝑃 = [√(𝜇𝑇)]𝑣𝑡2.
The quantity √(𝜇𝑇) represents the "impedance" of the medium in which the wave propagates (usually denoted by 𝛧).
Example 4.4 Find the power in a transverse mechanical wave with wave function 𝑦(𝑥, 𝑡) = 𝛢 sin(𝑘𝑥 - 𝜔𝑡).
For the harmonic wave the transverse velocity is 𝑣phase = √(𝑇/𝜇) and 𝑣phase = 𝜔/𝑘, so 𝑇 = 𝜇𝜔2/𝑘2. Thus
𝑃 = √(𝜇𝑇) 𝑣𝑡2 = √[𝜇 (𝜇 𝜔2/𝑘2)] 𝑣𝑡2 = 𝜇 𝜔/𝑘 𝑣𝑡2.
But for this wave 𝑣phase = -𝜔𝛢 cos(𝑘𝑥 - 𝜔𝑡), so
𝑃 = 𝜇 𝜔/𝑘 [-𝜔𝛢 cos(𝑘𝑥 - 𝜔𝑡)]2 = 𝜇 𝜔3/𝑘 [𝛢2 cos2(𝑘𝑥 - 𝜔𝑡)].
To find the average power, recall that the average value of cos2 over many cycles 1/2, so
𝑃avg = 𝜇 𝜔3/𝑘 [𝛢2(1/2)] = 1/2 𝜇𝛢2𝜔2(𝜔/𝑘) or
(4.24) 𝑃avg = 1/2 𝜇𝛢2𝜔2𝑣phase = 1/2 𝑍𝛢2𝜔2,
where impedance 𝑍 = √(𝜇𝑇) = √(𝜇2𝜔2/𝑘2) = 𝜇𝑣phase.
4.5 Wave impedance, reflection, and transmission
To understand the physical significance of impedance, consider the force that must be exerted by the source of a mechanical wave in order to produce the initial displacement of the material of the medium. In case of a transverse mechanical wave, the source must overcome the vertical component of the tension force. If the displacement of the string from the equilibrium position is 𝑦. the angle of the string with respect to the horizontal is 𝜃, the vertical component of the tension force is
𝐹𝑦 = 𝑇 sin 𝜃 ≈ 𝑇 ∂𝑦/∂𝑥.
For any single traveling wave, we can use Eq. (4.18)
𝐹𝑦 = 𝑇 (-1/𝑣phase) ∂𝑦/∂𝑡, and since ∂𝑦/∂𝑡 = 𝑣𝑡
𝐹𝑦 = 𝑇 (-1/𝑣phase) 𝑣𝑡 = -(𝑇/𝑣phase) 𝑣𝑡 or since 𝑣phase = √(𝑇/𝜇),
(4.25) 𝐹𝑦 = -[𝑇/√(𝑇/𝜇)] 𝑣𝑡 = -√(𝜇𝑇) 𝑣𝑡.
Thus the force needed to generated the wave is proportional to the transverse velocity of the string. Using 𝐹𝑦,source = -𝐹𝑦 helps make the meaning of impedance clearer:
(4.25) 𝑍 = √(𝜇𝑇) = 𝐹𝑦,source/𝑣𝑡.
So, for a mechanical wave, the impedance tells you the amount of force necessary to produce a given transverse velocity of the material displaced by the wave. In SI units, 𝑍 gives number of newtons needed to cause the material to move at a speed of m/s. But the higher-impedance string has more power than a lower-impedance string with the same transverse velocity as we can see in Eq. (4.21).
The analysis of the effect of changing media on a mechanical wave from Eq. (4.25) is the following:
(1) The medium produces a drag force on the source of the wave.
(2) hat drag force is proportional to the transverse velocity produced in the medium by the wave, and in the opposite direction (so 𝐹𝑦 𝛼 -𝑣𝑡).
(3) The constant of proportionality between the force and the transverse velocity is the impedance (𝑍) of the medium.
If the wave source is at the left end of the string and the right end is some finite-distance away, at the right end , the string might be clamped to a wall, it might be free, or it might be attached to another string with different linear density 𝜇 or elastic force, tension 𝑇. These situation are shown in Fig. 4.8.
And take a look at the situations shown in Fig. 4.9.. The first case shows an infinite string and that string presents a drag force of -𝑍𝑣1 to the source of the wave. Here there is no additional waves. The below cases are with dashed portions of string which are eliminated. What could we attach to the string at the right end that would produce a drag force equal to that of the missing portion of the string? The second case with a hanging mass would not be proportional to the transverse velocity of the incoming wave but the transverse acceleration according to Newton's second law. The third case with a spring would be proportional to the displacement according to Hooke's law. The last case with a "dashpot" - a mechanical device which resists motion using viscous friction would be proportional to the velocity but acts in the opposite direction. On replacing the missing portion of the infinite spring with a dashpot, the drag force has the same dependence on 𝑣1. We can think of that as adjusting impedance of the dashpot to match the impedance of the string. The dashpot is described also as a "purely resistive" device because if we terminate a finite string with a dashpot with the matching impedance with the string, the dashpot act a perfect absorber of the wave energy.
Now imagine hooking the right end of the string to another string, as shown Fig. 4. 10. If the second string has different values of linear mass density 𝜇2 or tension 𝛵2, and thus different impedance 𝑍2, we can determine how the wave will behave as follows. But it's necessary to enforce two boundary condition:
(1) the string is continuous, so the displacement (𝑦) must be the same on either side of the interface.
(2) the tangential force (-𝑇 ∂𝑦/∂𝑥) must be the same on either side of the interface.
Applying these boundary conditions leads to the following equation (we can see the details on the textbook's website):
𝑦reflected = (𝑍1 - 𝑍2)/(𝑍1 + 𝑍2) 𝑦incident,
where the factor (𝑍1 - 𝑍2)/(𝑍1 + 𝑍2) is called the amplitude reflection coefficient (𝑟):
(4.27) 𝑟 = (𝑍1 - 𝑍2)/(𝑍1 + 𝑍2).
So if 𝑟 = 1, the reflected wave has the same amplitude as the incident wave, and if 𝑟 = 0, there is no reflected wave. Alternatively 𝑟 can be negative and if 𝑟 = -1, for example, the reflected wave has the same amplitude as the incident wave.
If we want know the "transmitted wave" which propagates past the interface, a similar analysis show that
𝑦transmitted = 2𝑍1/(𝑍1 + 𝑍2) 𝑦incident,
So calling the amplitude transmission coefficient 𝑡, we can write
(4.28) 𝑡 = 2𝑍1/(𝑍1 + 𝑍2).
This tells us how the amplitude of the transmitted wave compares with the amplitude of the incident wave. If 𝑡 = 1, the transmitted wave has the same amplitude as the incident wave. But if 𝑡 = 0, the amplitude of the transmitted wave is zero. For any interface, 𝑡 = 1 + 𝑟, so so the values of 𝑡 can range from 0 to +2.
To apply the equation for 𝑟 and 𝑡 to a string with the right end clamped to a fixed position, consider that this is equivalent to making 𝑍2 = ∞. In this case
𝑟 = (𝑍1 - 𝑍2)/(𝑍1 + 𝑍2) = (𝑍1 - ∞)/(𝑍1 + ∞) = -1 and 𝑡 = 2𝑍1/(𝑍1 + 𝑍2) = 2𝑍1/(𝑍1 + ∞) = 0.
So here none of the incident wave's amplitude is transmitted past the interface, and the reflected wave ia an copy of the incident wave.
In the case which the right end of the string is left free by letting 𝑍2 = 0, the reflected wave has the same amplitude as the incident wave (𝑟 = 1).
Example 4.5 Consider a transverse pulse with maximum displacement of 2 cm propagating in the positive x-direction on a string with mass density 0.15 g/cm and tension 10 N. What happens if the pulse encounter a short section of string with twice the mass density and the same tension?
A sketch of this situation is shown in Fig. 4.11. 𝑍1 = 𝑍light and 𝑍2 = 𝑍heavy.
𝑍1 = √(𝜇light𝛵light) = √[(0.0015kg/m){10N)] = 0.387 kg/s,
𝑍2 = √(𝜇heavy𝛵heavy) = √[2(0.0015kg/m){10N)] = 0.548 kg/s.
𝑡 = 2𝑍1/(𝑍1 + 𝑍2) = (2)(0.387)/(0.387 + 0.548) = 0.83.
Thus in propagating from the light string to the heavy string the amplitude of the pulse is reduced to 83% of its original value at first (left) interface. But at the second (right) interface the impedances are 𝑍1 = 0.548 kg/s and 𝑍2 = 0.387kg/s. This means the transmission coefficient at the right interface
𝑡 = 2𝑍1/(𝑍1 + 𝑍2) = (2)(0.548)/(0.548 + 0.387) = 1.2,
so the amplitude is is reduced by a factor 0.83 times 1.2 and the final one is about 97% of its original value of 2 cm.
Consider what happens if we subtract the amplitude reflection coefficient 𝑟 from the amplitude transmission 𝑡:
𝑡 - 𝑟 = 2𝑍1/(𝑍1 + 𝑍2) - (𝑍1 - 𝑍2)/(𝑍1 + 𝑍2) = (2𝑍1 - 𝑍1 + 𝑍2)/(𝑍1 + 𝑍2) = (𝑍1 + 𝑍2)/(𝑍1 + 𝑍2) = 1 or 𝑡 = 1 + 𝑟.
In case of 𝑍2 much larger than 𝑍1 𝑟 approaches -1 and 𝑡 = 1 + 𝑟 = 1 + (-1) = 0, so the amplitude of transmitted wave should be zero. But in case of 𝑍1 much larger than 𝑍2 𝑟 approaches +1 and 𝑡 = 1 + 1 = 2. How can the amplitude of the transmitted wave possibly be 2? To understand the answer we have to consider the energy being carried by the reflected and transmitted waves. Recalling Eq. (4.24) that power of the wave 𝑃 is proportional to 𝑍𝐴: 𝑃 ∝ 𝑍𝐴2. Thus the ratio of the power in the transmitted wave to the power to the incident wave, called the power transmission coefficient 𝑇 is
(4.29) 𝑇 = 𝑃transmitted/𝑃incident = 𝑍2𝐴transmitted/𝑍1𝐴incident = (𝑍2/𝑍1) 𝑡2,
since 𝑡 is the ratio of the transmitted to the incident amplitude. But the reflected wave travels in the same medium as the incident wave, so the power reflection coefficient 𝑅 is
(4.30) 𝑅 = 𝑃reflected/𝑃incident = 𝑍1𝐴reflected/𝑍1𝐴incident = (𝑍1/𝑍1) 𝑟2 = 𝑟2,
So, for example, in case of 𝑍2 = 0, the power is entirely in the reflected wave since 𝑅 = 1 with none of the power in the transmitted wave since 𝑇 = 0. Since 𝑅 represented the fraction of the power of the incoming wave that is reflected and 𝑇 represented the fraction that is transmitted, the sum 𝑅 + 𝑇 must equal one.
(1) Small enough to allow us to make approximations such as cos 𝜃 ≈ 1 and sin 𝜃 ≈ tan 𝜃, which are good to within 10% if 𝜃 is less than 25∘.
(2) In Chapter 1 "displacement" may refer to any deviation from equilibrium, but in this case, 𝑦 is the actual distance from equilibrium position.
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015) |
|
|





































