|
김관석
|
2024-05-04 09:21:03, 조회수 : 150 |
- Download #1 : Wa_Fig_5s.jpg (893.1 KB), Download : 4

5 The electromagnetic wave equation
5.1 Properties of electromagnetic waves
An electromagnetic wave is also a disturbance from equilibrium that carries energy from one place to another. But unlike the mechanical waves electrical wave do not require a medium in which propagate. So they can propagates through vacuum and electric and magnetic fields are carry the energy.
One definition of a field is "a region in which forces act". We can test for the presence of such field: Place a charged particle in the region and measure the forces on that particle (our charged particle will have to be moving to detect a magnetic fields). Changes in those fields over space and time represent the "waving" of the waves.
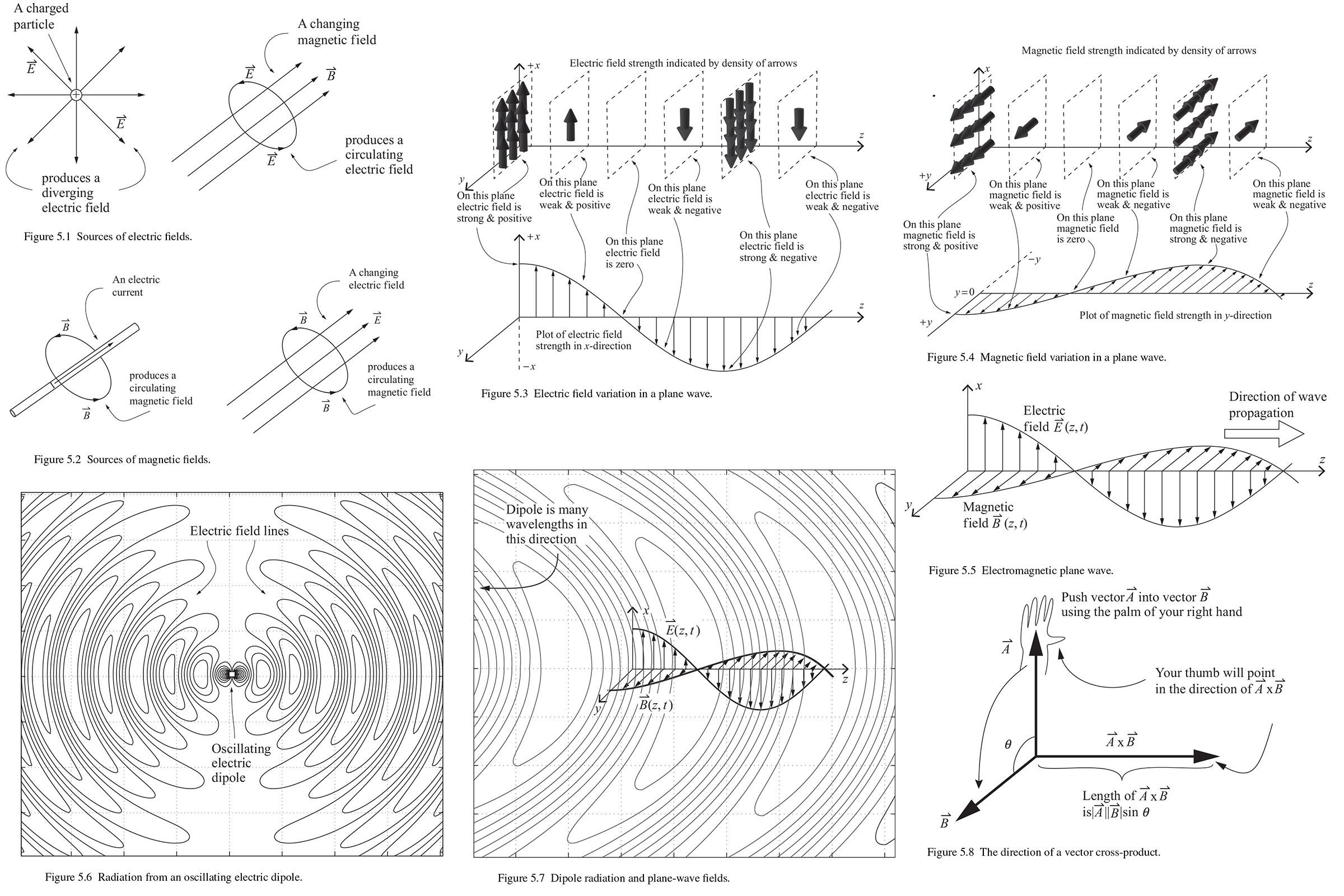
As we can see in Fig. 5.1 an electric field vector 𝑬 diverges from locations of positive charge. In the diagram arrows show the direction of the field and the density or length of those arrows indicates the strength of the field. The dimension of electric fields are force per charge, with SI units of newtons per coulomb (N/C), which are equivalent to volts per meter (V/m). Another source of electric fields is a changing magnetic field and the electric in that case circulates around and connects back upon itself. Such "induced" electric fields are an important component of electromagnetic waves. Sources of magnetic fields vector 𝑩 are shown in Fig. 5.2. Electric current produce a "magnetostatic" field that circulates around the current. And just as a changing magnetic field induces a circulating electric field, a changing electric fields induces a circulating magnetic field. The dimensions of magnetic fields are force divided by current times length, with SI units of newtons per coulomb-meter (N/C-m), which are equivalent to teslas (T). The vector electric field can be written as 𝑬 = 𝐸𝑥𝒊 + 𝐸𝑦𝒋 + 𝐸𝑧𝒌 and the vector magnetic field can be written as 𝑩 = 𝐵𝑥𝒊 + 𝐵𝑦𝒋 + 𝐵𝑧𝒌 in the Cartesian coordinate system.
The fundamental behavior of vector electric and magnetic fields, and their relationship to one another, are described by four equations known as Maxwell's equations. These equations originated in the work of Gauss, Faraday and Ampēre, but James Clerk Maxwell synthesized them and added a critical term to Ampēre law. The range of applicability of Maxwell's electromagnetic theory is among the greatest in physics. At the low-frequency long-wavelength end of the electromagnetic spectrum are extremely low-frequency {ELF) radio waves with a few hertz and wavelengths of 100,000 kilometers or longer. At higher frequencies and shorter wavelengths, electromagnetic waves are described as infrared, visible, ultraviolet, X-rays and gamma rays spanning a range of some 20 orders of magnitude and wavelength.
5.2 Maxwell's equations
Maxwell's equations are four vector equations: Gauss's law for electric fields, Gauss's law for magnetic fields, Faraday's law and the Ampēre-Maxwell law. Each of these equations may be written in integral or differential form. The integral forms describe the behavior of electric and magnetic fields over surfaces or around paths, while the differential forms apply to specific locations. But if we start with the differential form, the trip from Maxwell's equation to the wave equation is somewhat more direct.
Recalling the meaning of 𝛻 called "del" or "nabla", it is a differential operator telling us to take partial spatial derivatives (such as ∂/∂𝑥, ∂/∂𝑦, and ∂/∂𝑧) of the function on which we're operating. So the combination of symbols 𝛻 ∘ ("del dot") before 𝑨 is defined in Cartesian coordinate as
(5.1) 𝛻 ∘ 𝑨 = ∂𝐴𝑥/∂𝑥 + ∂𝐴𝑦/∂𝑦 + ∂𝐴𝑧/∂𝑧.
This operation is called "taking the divergence of 𝑨". The basic idea can be understood through an analogy with flowing fluids. For this analogy the vectors of a field are imagined to represent the flow of some substance toward or away from the location at which the divergence is being taken. If the field vectors are such that more material would flow away from a location than toward it, that location has positive divergence. If as much material would flow toward that point as away, the divergence is zero at that location. And if more material would flow toward the point than away, the divergence is negative there. The negative divergence soㅡsotimes called "convergence".
Another use of del operator in Maxwell's equation involves 𝛻 ⨯ ("del cross") and called "taking the curl of 𝑨" as
(5.2) 𝛻 × 𝑨 = (∂𝐴𝑧/∂𝑦 - ∂𝐴𝑦/∂𝑧)𝒊 + (∂𝐴𝑥/∂𝑧 - ∂𝐴𝑧/∂𝑥)𝒋 + (∂𝐴𝑦/∂𝑥 - ∂𝐴𝑥/∂𝑦)𝒌.
Again the basic idea can be understood through an analogy with flowing fluids. But in this case the issue is how strongly the field is circulating around the point under consideration. So a point at the center of a swirling vortex is a location of high curl, but smooth flow radially outward from a source has zero curl. The divergence produces a scalar result but the curl operator produces a vector result. Applying this concept to the fields in Fig. 5.2 should help us see that any location at which an electrical current or a changing electric fields is a location of non-zero curl of the magnetic field. With these concepts inhand we are ready to consider the differential form of Maxwell's equations.
(1) Gauss's law for electric fields: 𝛻 ∘ 𝑬 = 𝜌/𝜖0
It states that the divergence of the electric field at any location is proportional to the electric charge density (𝜌) at that location. That's because electrostatic field lines begin on positive charge and end on negative charge (hence the field lines tends to diverge away from location of positive charge and converge toward locations of negative charge). The symbol 𝜖0 represents the electric permittivity of free space.
(2) Gauss's law for magnetic fields: 𝛻 ∘ 𝑩 = 0
It tell us that the divergence of the magnetic field at any location must be zero. This is true because there is apparently no isolated "magnetic charge" in the Universe, so magnetic field lines neither diverge nor converge.
(3) Faraday's law: 𝛻 × 𝑬 = -∂𝑩/∂𝑡
It indicates that the curl of electric field at any location is equal to the negative of the time rate of change of magnetic field (∂𝑩/∂𝑡) at that location. That's because a changing magnetic field produces a circulating electric field.
(4) Ampēre-Maxwell law: 𝛻 × 𝑩 = 𝜇0𝑱 + 𝜇0𝜖0∂𝑬/∂𝑡
Ampēre's law, as modified by Maxwell, tell us that the curl of the magnetic field at any location is proportional to the electric current density 𝑱 plus the time rate of change of the electric field (∂𝑬/∂𝑡) at any location.(1) This is the case because a circulating magnetic field is produced both by an electric current and by a changing electric field. The symbol 𝜇0 represents the magnetic permeability of free space.
5.3 Electromagnetic wave equation
The real power of Maxwell's equations is realized by combining them together to produce the wave equation.
Start by taking the curl of both sides of Faraday's law
𝛻 × (𝛻 × 𝑬) = 𝛻 × (-∂𝑩/∂𝑡) = -∂(𝛻 × 𝑩)/∂𝑡,
where we're allowed to move the spatial partial derivatives of 𝛻 ⨯ inside the time partial derivative ∂/∂𝑡 for sufficiently smooth function. Then by inserting the expression for 𝛻 ⨯ 𝑩 from Ampēre-Maxwell law makes this
𝛻 × (𝛻 × 𝑬) = - ∂(𝜇0𝑱 + 𝜇0𝜖0∂𝑬/∂𝑡)/∂𝑡 = -𝜇0∂𝑱/∂𝑡 - 𝜇0𝜖0∂2𝑬/∂𝑡2.
The final step to electromagnetic wave equation require the use of the vector identity for the curl of the curl of a function
𝛻 × (𝛻 × 𝑨) = 𝛻 (𝛻 ∘ 𝑨) - 𝛻2𝑨.
in which 𝛻 (𝛻 ∘ 𝐀) represents the gradient (spatial change) of the divergence of 𝑨 and 𝛻2𝑨 represents the Laplacian of 𝑨, a vector operator involving second-order spatial partial derivatives. So we have
𝛻 (𝛻 ∘ 𝑬) - 𝛻2𝑬 = -𝜇0∂𝑱/∂𝑡 - 𝜇0𝜖0∂2𝑬/∂𝑡2
𝛻(𝜌/𝜖0) - 𝛻2𝑬 = -𝜇0∂𝑱/∂𝑡 - 𝜇0𝜖0∂2𝑬/∂𝑡2
in a vacuum, the charge density 𝜌 and the current density 𝑱 are both zero. Thus in free space
0 - 𝛻2𝑬 = 0 - 𝜇0𝜖0∂2𝑬/∂𝑡2 or
(5.3) 𝛻2𝑬 = 𝜇0𝜖0∂2𝑬/∂𝑡2.
In Cartesian coordinates those equations are
(5.4) ∂2𝐸𝑥/∂𝑥2 + ∂2𝐸𝑥/∂𝑦2 + ∂2𝐸𝑥/∂𝑧2 = 𝜇0𝜖0∂2𝐸𝑥/∂𝑡2 ∂2𝐸𝑦/∂𝑥2 + ∂2𝐸𝑦/∂𝑦2 + ∂2𝐸𝑦/∂𝑧2 = 𝜇0𝜖0∂2𝐸𝑦/∂𝑡2 ∂2𝐸𝑧/∂𝑥2 + ∂2𝐸𝑧/∂𝑦2 + ∂2𝐸𝑧/∂𝑧2 = 𝜇0𝜖0∂2𝐸𝑧/∂𝑡2.
We can find the equivalent equations for magnetic field 𝑩 in the similar way. Thus gives
(5.5) 𝛻2𝑩 = 𝜇0𝜖0∂2𝑩/∂𝑡2.
(5.6) ∂2𝐵𝑥/∂𝑥2 + ∂2𝐵𝑥/∂𝑦2 + ∂2𝐵𝑥/∂𝑧2 = 𝜇0𝜖0∂2𝐵𝑥/∂𝑡2 ∂2𝐵𝑦/∂𝑥2 + ∂2𝐵𝑦/∂𝑦2 + ∂2𝐵𝑦/∂𝑧2 = 𝜇0𝜖0∂2𝐵𝑦/∂𝑡2 ∂2𝐵𝑧/∂𝑥2 + ∂2𝐵𝑧/∂𝑦2 + ∂2𝐵𝑧/∂𝑧2 = 𝜇0𝜖0∂2𝐵𝑧/∂𝑡2.
Recalling the general equation for a propagating wave Eq. (2.11) in Chapter 2:
(2.11) ∂2𝜓/∂𝑥2 + ∂2𝜓/∂𝑦2 + ∂2𝜓/∂𝑧2 = (1/𝑣phase2)∂2𝜓/∂𝑡2.
Then we have
1/𝑣phase2 = 𝜇0𝜖0
(5.7) 𝑣phase = √(1/𝜇0𝜖0).
Hence the the velocity of an electromagnetic wave in a vacuum depends only on the electric permittivity 𝜖0 and magnetic permeability 𝜇0 of free space. The values of these constants can be determined experimentally using capacitors and inductors: the accepted values are 𝜖0 = 8.8541878 × 10-12 F/m and 𝜇0 = 4π × 10-7 H/m.(2) So we have
𝑣phase = √(1/𝜇0𝜖0) = √(1/8.8541878 × 10-12 F/m)(4π × 10-7 H/m) = 2.9979 × 108 m/s.
This is the speed of light in a vacuum, an astonishing result that caused Maxwell to conclude that light is an electromagnetic disturbance.
5.4 Plane-wave solutions to the electromagnetic wave equation
There are various solutions to the electromagnetic wave equations, one very important subset of those solutions involves plane waves. In plane wave, the surfaces of constant phase are flat plane perpendicular to the direction of propagation. We'll consider one propagating in the positive 𝑧-direction. So one solution for the electric field uses the harmonic function.
(5.8) 𝑬 = 𝑬0 sin(𝑘𝑧- 𝜔𝑡),
where 𝑬0 represents the "vector amplitude" of the propagating electric field. Likewise, the solution for the magnetic field can be written as
(5.9) 𝑩 = 𝑩0 sin(𝑘𝑧- 𝜔𝑡),
where 𝑩0 is the vector amplitude of the propagating magnetic field. In Cartesian coordinate, the components of the vector amplitudes of the electric and magnitude fields are
(5.10) 𝑬0 = 𝐸0𝒊 + 𝐸0𝒋 + 𝐸0𝒌 and
(5.11) 𝑩0 = 𝐵0𝒊 + 𝐵0𝒋 + 𝐵0𝒌.
In a vacuum 𝛻 ∘ 𝑬 = 0, which means
(5.12) ∂𝐸𝑥/∂𝑥 + ∂𝐸𝑦/∂𝑦 + ∂𝐸𝑧/∂𝑧 = 0.
But, since the phase of the wave must be constant over the entire (𝑥, 𝑦) plane, the electric field components cannot vary with 𝑥 or 𝑦. Hence ∂𝐸𝑥/∂𝑥 and ∂𝐸𝑦/∂𝑦 must be zero, which means that
∂𝐸𝑧/∂𝑧 = 0.
This equation says that, if the electric fields has a component in the 𝑧-direction, that component must be the same at all values of 𝑧. But a constant 𝐸𝑧 doesn't contribute to the wave disturbance. Thus a plane-wave electric field has no component in the direction of propagation. Since Gauss's law for magnetic field says that 𝛻 ∘ 𝑩 = 0, the same reasoning leads to the conclusion that 𝑩𝑧 must also equal zero for a plane wave propagating in the 𝑧-direction. And if 𝐸𝑧 = 0 and 𝐵𝑧 = 0, then both the electric and magnetic field must be perpendicular to the direction of propagation of the wave, Thus an electromagnetic plane wave is a transverse wave.
The possible components of such a wave are therefore
𝐸𝑥 = 𝐸0𝑥 sin(𝑘𝑧- 𝜔𝑡), 𝐵𝑥 = 𝐵0𝑥 sin(𝑘𝑧- 𝜔𝑡),
𝐸𝑦 = 𝐸0𝑦 sin(𝑘𝑧- 𝜔𝑡), 𝐵𝑦 = 𝐵0𝑦 sin(𝑘𝑧- 𝜔𝑡).
Just as Gauss's law allowed us to eliminate the 𝑧-component of the electric and magnetic fields, Faraday's law can be used to find the relationship among the remaining components:
𝛻 × 𝑬 = -∂𝑩/∂𝑡
Using the definition of the curl in Cartesian coordinate Eq. (5.2), the 𝑥-component is
(∂𝐸𝑧/∂𝑦 - ∂𝐸𝑦/∂𝑧) = -∂𝐵𝑥/∂𝑡,
which leads to the following result:
𝐸𝑥 = 𝐸0𝑥 sin(𝑘𝑧 - 𝜔𝑡), 𝐸𝑦 = 𝐸0𝑦 sin(𝑘𝑧 - 𝜔𝑡), 𝐸𝑧 = 0; 𝐵𝑥 = 𝐵0𝑥 sin(𝑘𝑧 - 𝜔𝑡), 𝐵𝑦 = 𝐵0𝑦 sin(𝑘𝑧 - 𝜔𝑡), 𝐵𝑧 = 0.
(∂𝐸𝑧/∂𝑦 - ∂𝐸𝑦/∂𝑧) = 0 - ∂[𝐸0𝑦 sin(𝑘𝑧- 𝜔𝑡)]/∂𝑧 = -𝑘𝐸0𝑦 cos(𝑘𝑧 - 𝜔𝑡); -∂𝐵𝑥/∂𝑡 = -∂[𝐵0𝑥 sin(𝑘𝑧 - 𝜔𝑡)]/∂𝑡 = 𝜔𝐵0𝑥 cos(𝑘𝑧 - 𝜔𝑡).
-𝑘𝐸0𝑦 cos(𝑘𝑧 - 𝜔𝑡) = 𝜔𝐵0𝑥 cos(𝑘𝑧 - 𝜔𝑡). -𝑘𝐸0𝑦 = 𝜔𝐵0𝑥, 𝐸0𝑦 = -𝜔/𝑘𝐵0𝑥 = -𝑣𝐵0𝑥 = -𝑐𝐵0𝑥. so we have
(5.13) 𝐸0𝑦 = -𝑐𝐵0𝑥.
The 𝑦-component leads to (in the similar way):
(5.14) 𝐸0𝑥 = 𝑐𝐵0𝑦.
Example 5.1 If the eletromagnetic plane wave is propagating along the positive 𝑧-direction and its electric field at a certain location points along the 𝑥-axis, in what direction does the wave's magnetic field points at that location?
If 𝐸0𝑥 is positive, then 𝐸0𝑦 = 0. Because 𝐵0𝑦 = 𝐸0𝑥/𝑐, 𝐵0𝑦 is also positive and 𝐵0𝑥 must also be zero. So the magnetic field must point entirely along the positive 𝑦-axis at this location.
A sketch of the electric filed of an electromagnetic wave is shown in Fig. 5.3. And a corresponding sketch for the magnetic field at the same location in time is shown in Fig. 5.4. Combining the field-strength plots from both figures results in the plot shown in Fig. 5.5. In this figure, the plot of the magnetic field has been scaled to have the same amplitude as the electric field for clarity, but the actual relative magnitude of the field strengths can be found as
∣𝑬∣ = √ [(𝐸0𝑥)2 + (𝐸0𝑦)2] = √ [(𝑐𝐵0𝑦)2 + (-𝑐𝐵0𝑥)2] = 𝑐√ [(𝐵0𝑦)2 + (𝐵0𝑥)2] = 𝑐∣𝑩∣ or
(5.15) ∣𝑬∣/∣𝑩∣ = 𝑐
which says that electric field strength (in V/m) is bigger than the magnetic field strength (in T) by a factor of 𝑐 (in m/s).
The direction of the electric fields defines the "polarization" of the wave, if the electric fields remain in the same plane, the wave is said to be linearly polarized or plane polarized. There are more complex electromagnetic waves. For example, consider the plot of the radiation from an oscillating electric dipole shown in Fig. 5.6.This plot is often called "radiation patterns" and is a 2-dimensional slice through the 3-dimensional radiation pattern.
Far from the dipole the electromagnetic wave produced by an oscillating dipole resemble plane waves to a good approximation. To help us understand that relationship, we can refer to Fig. 5.7 where is a small, properly scaled version of the electric and magnetic plane-wave diagram.
5.5 Energy, power, and impedance of electromagnetic waves
To understand the energy stored in electric and magnetic fields, it's helpful to consider the energy stored in a charged capacitor and in a current-carrying inductor. That's because the charge stored on a capacitor produces an electric field between the plates, and the current flowing through an inductor produces a magnetic field. By calculating the amount of work done in establishing those fields , the energy stored there may be determined. If we divide that energy by volume it occupies, we'll get the energy density with SI units of J/m3.
The energy density for the electric field in a vacuum is
(5.16) 𝑢𝐸 = (1/2)𝜖0∣𝑬∣2,
where 𝜖0 is the electric permittivity of free space. For the magnetic field in a vacuum, the energy density 𝑢𝐵 is
(5.17) 𝑢𝐵 = (1/2𝜇0)∣𝑩∣2,
where 𝜇0 is the magnetic permeability of free space. So total energy density may be found by combining Eqs. (5.16) and (5.17):
𝑢tot = (1/2)𝜖0∣𝑬∣2 + (1/2𝜇0)∣𝑩∣2. Because ∣𝑬∣/∣𝑩∣ = 𝑐, so
𝑢tot = (1/2)𝜖0∣𝑬∣2 + (1/2𝜇0)(∣𝑬∣/𝑐)2
But 𝑐 = 1/√(𝜇0𝜖0) according to Eq. (5.7)
𝑢tot = (1/2)𝜖0∣𝑬∣2 + (𝜇0𝜖0/2𝜇0)(∣𝑬∣)2 = (1/2)𝜖0∣𝑬∣2 + (1/2)𝜖0∣𝑬∣2
(5.19) 𝑢tot = 𝜖0∣𝑬∣2.
Eliminating ∣𝑬∣ rather than ∣𝑩∣ results in
(5.20) 𝑢tot = (1/𝜇0)∣𝑬∣2.
Because the energy is moving at the speed of light 𝑐 in free space, if we multiply 𝑢tot (in J/m3) by 𝑐 (in m/s), we get unit of J/s m3. That's the rate at which energy flows through a cross-sectional area of one square meter perpendicular to the direction of the wave. Since energy per unit time (J/s) is power (watt), the magnitude of the power per unit area in an electromagnetic wave is
∣𝑺∣ = 𝑢tot𝑐,
in which power density is written as the magnitude of a vector 𝑺 called the "Poynting vector" named after J Henry Poiynting.
∣𝑺∣ = 𝑢tot𝑐 = 𝜖0∣𝑬∣2𝑐 = 𝜖0∣𝑬∣2√(1/𝜇0𝜖0)
(5.21) ∣𝑺∣ = √(𝜖0/𝜇0)∣𝑬∣2.
The average of the power density over time is defined using the average of the square of magnitude of electric field
∣𝑬∣2 = ∣𝑬0𝑥∣2[sin(𝑘𝑧 - 𝜔𝑡)]2
∣𝑬∣2avg = ∣𝑬0𝑥∣2[sin(𝑘𝑧 - 𝜔𝑡)]2avg
But the average of sin2 function over many cycles is 1/2, since ∫0πsin2𝑥 𝑑𝑥 = π/2. [Re Wolframalpha] so
∣𝑬∣2avg = (1/2)∣𝑬0∣2
(5.22) ∣𝑺∣avg = (1/2)√(𝜖0/𝜇0)∣𝑬0𝑥∣2.
Example 5.2 At the surface of the Earth, the average power density of sunlight on a clear day is approximately 1,300 W /m. Find the average magnitude of the electric and magnetic fields in sunlight.
∣𝑺∣avg = (1/2)√(𝜖0/𝜇0)∣𝑬0𝑥∣2; ∣𝑬0𝑥∣ = √[2∣𝑺∣avg/√(𝜖0/𝜇0)] = √[2∣𝑺∣avg√(𝜇0/𝜖0)] = √[(2)(1,300 W/m2)√{(4π × 10-7 H/m)/(8.8541878 × 10-12 F/m)}] ≈ 990 V/m.
∣𝑩0𝑥∣ = ∣𝑬0𝑥∣/𝑐 = (990 V/m)/(3 × 108 m/s) ≈ 3.3 × 10-6 T.
The term √(𝜇/𝜖) is the electromagnetic impedance (usually designated as 𝑍, which plays as analogous role in the mechanical impedance. In free space the electromagnetic impedance is
(5.23) 𝑍0 = √(𝜇0/𝜖0) = √[(4π × 10-7 H/m)/(8.8541878 × 10-12 F/m)] ≈ 377 Ω,
The impedance of other material is given by 𝑍 = √(𝜇/𝜖) (𝜇: the magnetic permeability of the material, 𝜖: the electric permittivity of the material). When an electromagnetic wave impinges on a boundary between materials with different electromagnetic impedance, the amplitudes of the reflected and transmitted waves depend on the impedance difference between the media.
In free space according to Eqs. (5.21) and (5.22) we have
(5.24) ∣𝑺∣ = ∣𝑬∣2/𝑍0 and
(5.25) ∣𝑺∣avg = ∣𝑬∣2avg/𝑍0.
Here's the most common way of writing the Poynting vector:
(5.26) 𝑺 = (1/𝜇0)𝑬 × 𝑩.
The magnitude and direction of the vector cross-produce are illustrated in Fig. 5.8:
(5.27) ∣𝑨 × 𝑩∣ = ∣𝑨∣∣𝑩∣sin 𝜃, where 𝜃 is the angle between 𝑨 and 𝑩.
Example 5.3 Use the definition of Poynting vector from Eq. (5.26) to find the vector power density 𝑺 of an electromagnetic plane wave propagating along the positive z-axis.
𝑺 = (1/𝜇0)𝑬 × 𝑩 = (1/𝜇0)∣𝑬∣∣𝑩∣sin 𝜃 𝒌 = (1/𝜇0)∣𝑬∣∣𝑩∣sin 90∘ 𝒌 = (1/𝜇0)∣𝑬∣∣𝑩∣𝒌 = 𝜇0)∣𝑬∣(∣𝑬∣/𝑐)𝒌 = 𝜇0)∣𝑬∣21/√[1/(𝜇0/𝜖0)]𝒌 = √(𝜖0/𝜇0)∣𝑬∣2𝒌 = (∣𝑬∣2/𝑍0)𝒌,
as expected from Eq. (5.24).
(1) The term involving the changing electric field is the "displacement current" added to Ampēre's law by James clerk Maxwell.
(2) Farads are units of capacitance, equivalent C2 s2/kg m2, and henries are units of inductance equivalent to m2 kg/C2.
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015)
|
|
|





































