|
김관석
|
2024-05-07 09:24:42, 조회수 : 164 |
- Download #1 : Wa_Fig_6s.jpg (717.5 KB), Download : 2
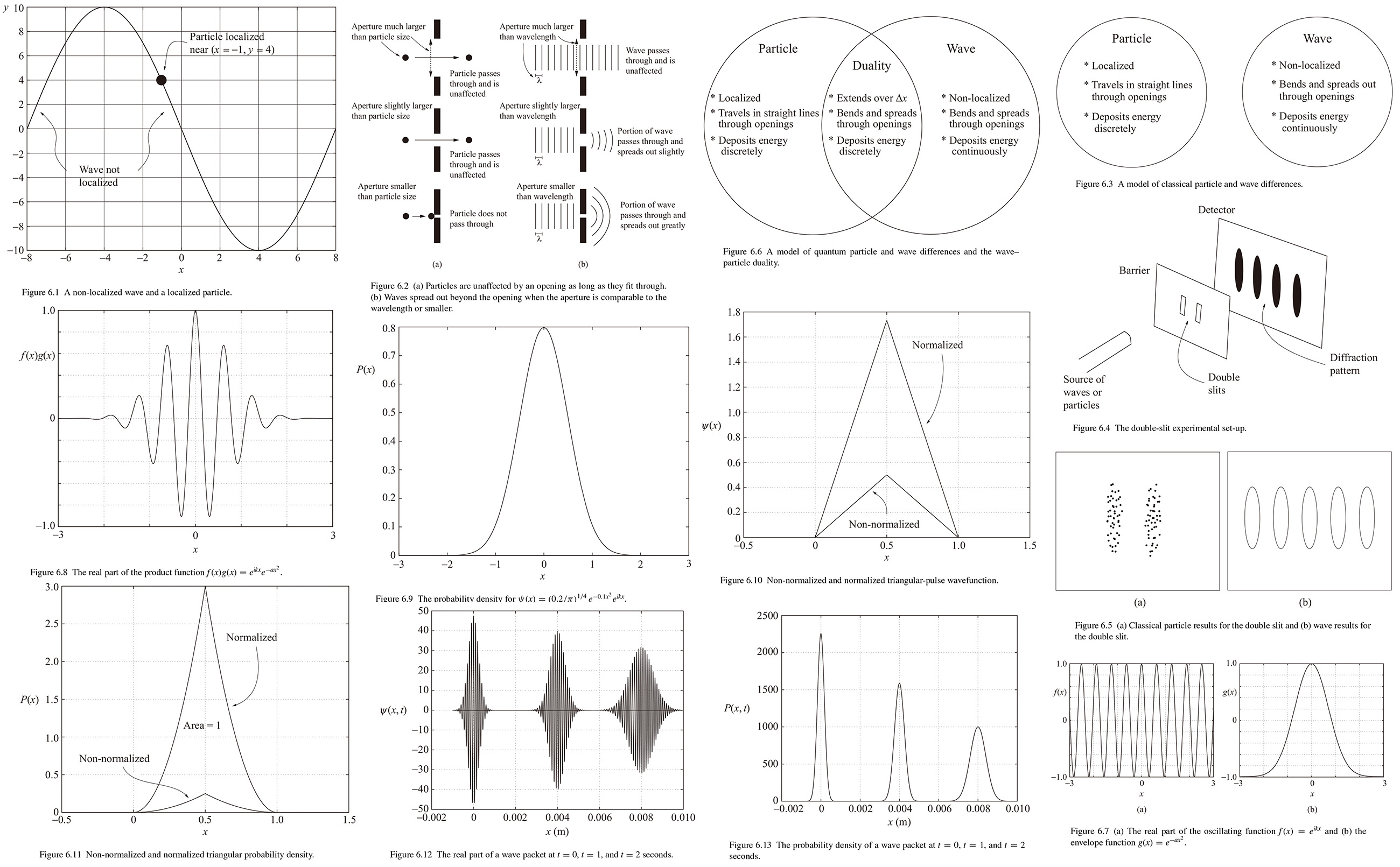

6 The quantum wave equation
6.1 Waves and particle characteristics
Before studying modern physics, we think of particles and waves as belonging to fundamentally different categories of objects. Here's a summary of some of the different characteristics between particles and waves.
Occupying space. Particles exist in a well-defined around of space: This property means particles are "localized". But waves exist over an extended region of space. For example a harmonic functions exist over all values of 𝑥 from -∞ to +∞. So a single-frequency wave is inherently non-localized. These difference are illustrated in Fig. 6.1.
Traveling through openings. As shown in Fig. 6.2, a particle passes through an opening larger than the particle and is not affected, but if the aperture is smaller than particle size it can't pass through. Waves, however, behave quite differently. If the aperture is much larger than wavelength, it passes through and is unaffected. But if we reduce the opening so that the aperture is similar to the wavelength of the wave, the portion of the wave that passes through it is no longer plane wave, The surfaces of constant phase are somewhat curved and the wave spreads out after passing through the opening. And if we make the aperture smaller than the wavelength, the wavefront curvature and spreading out of the wave becomes even greater. This effect is called "diffraction".
Interacting with other particles and waves. Particles interact with other particles via collisions, and when particles collide they can exchange momentum and energy. When particles collide, they quickly exchange a discrete amount of energy, and momentum and according to conversation laws the total momentum and energy of the system is the same before and after. Wave, however, interact with other waves via superposition. When two or more waves occupy the small region of space, the resulting wave is the sum of all contributing waves. The waves are said to "interfere" with another. Wave can also interact with objects and in such interactions some of the wave's energy can be transferred and occurs over an extended period of time.
A summary of the classical-mechanics model of some distinction between particles and waves is given in the diagram in Fig. 6.3.
6.2 Wave-particle duality
To understand wave-duality, it's helpful to consider the type of experiment we could perform on a particle to test for wave behavior. However, in order to detect a particle's wave behavior, the aperture must be comparable to the wavelength of the wave. That means that it's necessary to predict the wavelength from the properties of the particle.
Due to the work of Louis de Broglie who hypothesized the existence of matter waves in 1924 the prediction is possible. Almost two decades before Albert Einstein had shown that light exhibits characteristics of both waves and particles, behaving like waves when passing through slits, but acting like particle (called photon) during interactions such as the photoelectric effect. De Broglie made the inspired guess that the wave-particle duality extends to electrons and other particles with mass. As he wrote in his PhD thesis: "My essential idea was to extend to all particles the coexistence of waves and particles discovered by Einstein in 1905 in the case of light and photons."
To understand de Broglie's expression for the wavelength of a particle, consider Einstein's relationship for the energy of a photon with frequency 𝜈 and wavelength 𝜆:
(6.1) 𝛦 = 𝘩𝜈 = 𝘩𝑐/𝜆,
where 𝘩 is Planck's constant (6.626 × 10-24 m2 kg/s) and 𝑐 is the speed of light. Although photons have no rest mass, they do carry momentum, and the magnitude of the momentum is related to the photon's energy by
(6.2) 𝑝 = 𝛦/𝑐. This gives
𝛦 = 𝘩𝑐/𝜆 = 𝑐𝑝, 𝑝 = 𝘩/𝜆, 𝜆 = 𝘩/𝑝.
If this relationship holds also for particles with mass, then since 𝑝 = 𝑚𝑣, we have
(6.3) 𝜆 = 𝘩/𝑝 = 𝘩/𝑚𝑣.
Consider the implication of Eq (6.1). This is why only moving particles exhibit wave behavior. Also because Planck's constant is such a small number, the wave characteristic of everyday objects are not appeared since their high mass makes de Boglie wavelength too small to measure.
Example 6.1 What is the de Broglie wavelength of a 75-kg human walking at speed of 1.5 m/s?
The human has momentum 𝑝 = 𝑚𝑣 = 75 kg × 1.5 m/s = 113 kg m/s, so the de Broglie wavelength is
(6.4) 𝜆 = 𝘩/𝑝 = (6.626 × 10-34 J/s)/(113 kg m/s) = 5.9 × 10-36.
That is billions times smaller than the protons and neutrons. Hence a human body does not demonstrate the wave behavior of matter.
Example 6.2 What is the de Broglie wavelength of an electron that has passes through a potential difference of 50 volts?
After passing through a potential difference of 50 volts, an electron has 50 eV of energy. 1 eV = 1.6 ×10-19 J, so
(6.5) (50 eV)(1.6 ×10-19 J/1 eV) = 8 ×10-18 J.
We can use the classical expression for kinetic energy 𝐾𝐸:
(6.6) 𝐾𝐸 = (1/2)𝑚𝑣2
(6.7) 𝐾𝐸 = (1/2)𝑚𝑣2 = (1/2𝑚)𝑚2𝑣2 = 𝑝2/2𝑚.
In this case, the electron's energy 𝐸 is all kinetic, so 𝐸 = 𝐾𝐸:
(6.8) 𝑝 = √(2𝑚𝐸).
𝑝 = √(2𝑚𝐸) = √(2 × 9.1 ×10-31 kg × 8 ×10-18 J) = 3.8 ×10-24 kg m/s. So the de Broglie wavelength is
(6.9) 𝜆 = 𝘩/𝑝 = (6.626 × 10-34 J/s)/(3.8 ×10-24 kg m/s) = 1.7 × 10-10 m.
This is similar to the spacing between atoms in a crystal array, such an array can be used to experimentally determine a moving electron's wavelenghth.
That experiment was done by Clinton Favisson and Lester Germer in 1927. Knowing that waves scattered from crystals produce a diffraction pattern, they bombarded a nickel crystal with electrons and looked for evidence of diffraction. They found it, and then they used the scattering angle and knowing spacing of the atoms in the crystal to calculate the wavelength of the electrons. Their results were in good agreement with de Broglie's expression for the wavelength of particles with the mass and velocity of the electrons used in the experiment.
A similar, but conceptually more straightforward experiment in double slit, which is often used to demonstrate the wave properties of light. as in Fig. 6.4 with a source of waves or particles facing a barrier with two small slits a short distance apart: far behind the barrier is a detector.
First consider when the source emits a continuous stream of wave. According to Huygens's principle, every point on a wavefront can be considered to be the source of another wave that spreads out spherically from that point. When the wave encounters the barrier, most of the secondary waves are blocked; only two small portions of wavefront pass through the slits. The spherically expanding secondary waves from those two portions of the wavefront then travel to the detector, where they superimpose to produce the resultant waveform. But the waves from the two slits arrive at the detector with different phase. Depending on the the amount of that phase difference, the two waves may add or subtract and the interference may be constructive or destructive. At points of constructive interference, a bright fringe appears; and at points of destructive interference, a dark fringe appears.
Now imagine that the source fires a stream of particles such as electrons at the barrier. Since streaming electrons also have characteristic of waves, the detector registers a continuous accumulation of energy in an interference pattern, as shown in the right portion in Fig. 6.5.
Finally, consider when individual electrons are sent through the slits one at a time. The accumulation of the points creates the dark and light fringes of an interference pattern. Evidently each electron interfere with itself as it pass through both slits.
The modern understanding of wave-particle duality is shown in Fig. 6.6. When a quantum-mechanical object is traveling, it acts like a wave, and it bends around corners, diffracts through small openings, and interferes. When a quantum-mechanical object is depositing or accepting energy, it acts like a particle. And a quantum-mechanical object behaves like a traveling wave packet that occupies a small, but finite, amount of space.
6.3 The Schrödinger equation
Understanding that electrons can behave like waves comes from the interpretation of wavefunction, 𝜓(𝑥, 𝑡), the solution to the Schrödinger equation which governs these matter waves. Although Richard Feynmann once said that it's not possible to derive the Schrödinger equation from anything we know, we can get a sense of Schrödinger's reasoning by starting with an expression for the energy of a particle. If that particles is moving non-relativistically (slowly relative to the speed of the light 𝑐), and the forces acting on the particle are conservative, the total mechanical energy 𝛦 of that particle may be written as
(6.10) 𝛦 = 𝐾𝛦 + 𝑉 = (1/2)𝑚𝑣2 + 𝑉 = 𝑝2/2𝑚 + 𝑉,
where 𝐾𝛦 is the kinetic energy and 𝑉 is the potential energy.
Schrödinger referred to Einstein's relationship of energy of a photon 𝛦 = 𝘩𝜈 Eq. (6.1), and wrote a version this equation for energy associated with matter waves as follows:
(6.11) 𝛦 = 𝘩𝜈 = (𝘩/2π)(2π 𝜈) = ℏ𝜔,
where "reduced Planck constant" ℏ = 𝘩/2π, frequency 𝜆 = 𝜈, and the angular frequency 𝜔 = 2π 𝜈. So we have
(6.12) ℏ𝜔 = (1/2)𝑚𝑣2 + 𝑉.
De Broglie's equation Eq. (6.3) relating momentum to wavelength can be expressed
(6.13) 𝑝 = 𝘩/𝜆 = 𝘩/(2π/𝑘) = (𝘩/2π)𝑘 = ℏ𝑘
So we can write Eq. (6.12) as
(6.14) ℏ𝜔 = ℏ2𝑘2/2𝑚 + 𝑉.
To get from this equation to the Schrödinger equation, assume the matter wave associated with the particle can be written as the harmonic wavefunction 𝜓(𝑥, 𝑡):
(6.15) 𝜓(𝑥, 𝑡) = 𝛢𝑒𝑖(𝑘𝑥-𝜔𝑡) = 𝑒-𝑖𝜔𝑡(𝛢𝑒𝑖𝑘𝑥).
Notice that we've divided the exponential term the time-dependent term from the space-dependent term. Then we can get the first and and second derivatives with respect to time 𝑡 or space 𝑥:
(6.16) ∂𝜓/∂𝑡 = [∂(𝑒-𝑖𝜔𝑡)/∂𝑡](𝛢𝑒𝑖𝑘𝑥) = -𝑖𝜔(𝑒-𝑖𝜔𝑡)(𝛢𝑒𝑖𝑘𝑥) = -𝑖𝜔𝜓.
(6.17) ∂𝜓/∂𝑥 = 𝑒-𝑖𝜔𝑡∂(𝛢𝑒𝑖𝑘𝑥)/∂𝑥 = 𝑖𝑘𝑒-𝑖𝜔𝑡(𝛢𝑒𝑖𝑘𝑥) = 𝑖𝑘𝜓.
(6.18) ∂2𝜓/∂𝑥2 = 𝑒-𝑖𝜔𝑡∂2(𝛢𝑒𝑖𝑘𝑥)/∂𝑥2 = (𝑖𝑘)2(𝛢𝑒𝑖𝑘𝑥) = -𝑘2𝜓.
Before fitting these derivatives into Eq. (6.14) we are to multiply Eq. (6.16) by 𝑖ℏ at Eq. (6.16)
𝑖ℏ(∂𝜓/∂𝑡) = 𝑖ℏ(-𝑖𝜔𝜓) = ℏ𝜔𝜓 or ℏ𝜔 = (𝑖ℏ/𝜓)(∂𝜓/∂𝑡).
Now we can plug this into Eq. (6.14):
(𝑖ℏ/𝜓)(∂𝜓/∂𝑡) = ℏ2𝑘2/2𝑚 + 𝑉 or 𝑖ℏ(∂𝜓/∂𝑡) = (ℏ2𝑘2/2𝑚)𝜓 + 𝑉𝜓.
But we know that 𝑘2𝜓 = -∂2𝜓/∂𝑥2 from Eq. (6.18), so
(6.19) 𝑖ℏ(∂𝜓/∂𝑡) = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2) + 𝑉𝜓.
This is the one-dimensional time-dependent Schrödinger equation. Note that the presence of "𝑖" as a multiplicative factor means the the solutions will generally complex. We can derive a "time-independent" version by using Eq. (6.16) to replace ∂𝜓/∂𝑡 by -𝑖𝜔𝜓:
(6.20) 𝑖ℏ(-𝑖𝜔𝜓) = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2) + 𝑉𝜓 or ℏ𝜔𝜓 = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2) + 𝑉𝜓.
Since 𝛦 = ℏ𝜔 Eq. (6.11) we may also see this equation written as
(6.21) 𝛦𝜓 = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2) + 𝑉𝜓 or
(6.22) (𝛦 -𝑉)𝜓 = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2).
We must note that the wavefunction 𝜓 is still 𝜓(𝑥, 𝑡) and it's essentially an expression of the conservation of energy: 𝛦 -𝑉 is the kinetic energy. So the equation tells us that the kinetic energy of the particle is proportional to the second spatial derivative of 𝜓, which is the curvature of the wavefunction. Greater curvature with 𝑥 means that the waveform has a higher spatial frequency, which means it has shorter wavelength, and de Brogle's equation relates shorter wavelength to higher momentum.
Example 6.3 What is the time-independent Schrödinger equation for a free particle?
In this context "free" means the particle is free from the influence of external force. Because a free particle travels in a region of constant potential energy and reference location of zero potential energy is arbitrary, we can set 𝑉 = 0 in Eq. (6.22). So
(6.23) 𝛦𝜓 = (-ℏ2/2𝑚)(∂2𝜓/∂𝑥2) or
(6.24) ∂2𝜓/∂𝑥2= - (2𝑚𝛦/ℏ2) 𝜓.
Since the total energy of a free particle equals the particle's kinetic energy, we can set 𝛦 = 𝑝2/2𝑚:
(6.25) ∂2𝜓/∂𝑥2= - (𝑝2/ℏ2) 𝜓.
This is the Schrödinger equation for a free particle. It's instructive to compare with Eq. (3.22) for standing wave, which is assumed to be the product of a function 𝑋(𝑥) that depends only on 𝑥 and another function 𝑇(𝑡) that depends only on 𝑡. The equation is
(3.22) ∂2𝑋/∂𝑥2 = 𝛼𝑋 = -𝑘2,
which is identical to Eq. (6.25), provided that
𝑝2/ℏ2 = -𝑘2. so 𝑝2/ℏ2 = (2π/𝜆)2 or
𝑝/ℏ = 𝑝/𝘩/(2π) = (2π/𝜆) or 𝜆 = 𝘩/𝑝,
which is de Broglie's expression Eq. (6.3) for the wavelength of matter wave. For a free particles, oscillation frequency and energy may take on any value, but particles in the regions in which the potential energy varies may be constrained to certain values of frequency and energy that depend on the boundary conditions. Thus the allowed energies of a particle in a potential well can be quantized.
This means that the wave characteristic of a particle is analogous to a standing wave, and the energy of a particle is proportional to the oscillation frequency of that standing wave. We may see solutions to the time-independent Schrödinger equation referred to as"stationary states", but we should note that this means that the energy of the system is constant over time, not that the wavefunction is stationary.
6.4 Probability wavefunctions
At first Schrödinger thoght that the wavefunction 𝜓(𝑥, 𝑡) was the charge density of electron. However, MaxBorn was able to offer his own explanation, which is now the modern interpretation of wavefunction. It is a "prpbability amplitude" related to the probability of finding the particle in a given region of space. The quantity is called an amplitude because just as we must square the amplitudeto get its energy in Eq. (4.22), so we must square the wavefunctin to get a probability density 𝓟. Since the wavefunction is generally complex, we square it by multiplying it by its complex conjugate:
(6.26-27) 𝓟(𝑥, 𝑡) = 𝜓*(𝑥, 𝑡)𝜓(𝑥, 𝑡) or 𝓟(𝑥, 𝑡) = ∣𝜓(𝑥, 𝑡)∣2.
The probability density is the probability per unit length in one dimension, per unit area in two dimension and per unit volume in three dimension. 𝓟 tells us how the probability of finding the particle in a particular place is spread out through space at any given time. This answers the question of what's waving for an electron and other quantum-mechanical objects: A traveling particle is actually traveling lump of probability amplitude. When it encounter an obstacle (such as the two slits described in Section 6.2), the waving probability amplitude is diffracted according to the wavelength. When interact (which is how it is measured or detected), this wavefunction collapses to the single measured result. This result is discrete, which is consistent with particle behavior.
So we can write the wavefunction for a free particle using harmonic function. Since 𝓟(𝑥, 𝑡) represents the probability density, integrating overall space (𝑥 = -∞ to 𝑥 = ∞) should give a probabilty of one. So
(6.28-31) 𝜓(𝑥, 𝑡) = 𝐴𝑒𝑖(𝑘𝑥-𝜔𝑡), 1 = ∫-∞ ∞𝜓*(𝑥, 𝑡)𝜓(𝑥, 𝑡)𝑑𝑥, 1 = ∫-∞ ∞𝐴*𝐴𝑒-𝑖(𝑘𝑥-𝜔𝑡)𝑒𝑖(𝑘𝑥-𝜔𝑡)𝑑𝑥, 1 = 𝐴*𝐴(∞).
But since nothing can multiply to give one, this waveform is "non-normalizable". To modify the wavefunctin of Eq. (6.28) and to form quantum wave packet, the Fourier concepts are very useful as we'll see in the next section.
6.5 Quantum wave packets
Since a particles localized in space, so it seems reasonable to expect that its wave should also be spatially limited: that is, it should be a wave packet. To form a wave pocket some waves with different but similar wavelength must be included. A range of wavelength means arrange of wavenumber, and a range of wavenumber means a range of momenta (since 𝑝 = ℏ𝑘). So the challenge is to find a wave packet that is localized in space over a region 𝛥𝑥 but that travels with a well-defined momentum 𝑝 = ℏ𝑘0, where 𝑘0 represents the dominant wavenumber.
It's a bit easier to write 𝜓(𝑥, 𝑡) = 𝑓(𝑡)𝜓((𝑥) allow us to concentrate on localizing the spatial term 𝜓((𝑥); the effect of the time term 𝑓(𝑡) will be considered later. And one approach to limiting the spatial extent of the wavefunction is to write 𝜓((𝑥) as the product of two functions: the exterior" envelope 𝑔(𝑥), and the "interior" oscillations 𝑓(𝑥),
(6.32) 𝜓((𝑥) = 𝑔(𝑥)𝑓(𝑥).
If the envelope function goes to zero everywhere except at a certain range of 𝑥 values, then the oscillations of the wave packet will be localized to that range.
For example, consider the single-wavelength oscillating function 𝑓(𝑥) = 𝑒𝑖𝑘𝑥 (= cos𝑘𝑥 + 𝑖sin𝑘𝑥) as the plot of the real part of 𝑓(𝑥) in Fig. 6.7 (a)(𝑘 = 10), this function extends over all space. And consider the envelope function 𝑔((𝑥) given by
(6.33) 𝑔(𝑥) = 𝑒-𝑎𝑥2.
As we can see in Fig. 6.7 (b)(𝑎 = 1), this function reaches a peak of 𝑔(𝑥) at 𝑥 = 0 and decreases both directions at a rate determined by 𝑎.
Multiplying this envelope function 𝑔(𝑥) by the oscillating function 𝑓(𝑥) causes the product function 𝑓(𝑥)𝑔(𝑥) as (the real part) shown in Fig. 6.8. So the probability density is
𝜓 = 𝑒𝑖𝑘𝑥𝑒-𝑎𝑥2, 𝜓* = 𝑒-𝑖𝑘𝑥𝑒-𝑎𝑥2,
𝓟 = ∣𝜓*𝜓∣ = (𝑒-𝑖𝑘𝑥𝑒-𝑎𝑥2)(𝑒𝑖𝑘𝑥𝑒-𝑎𝑥2) = 𝑒-2𝑎𝑥2.
Integrating this over all space gives
𝓟all space = ∫-∞ ∞𝑒-2𝑎𝑥2𝑑𝑥 = √(π/2𝑎). [Re Wolframalpha]
So to set 𝓟all space = 1, 𝜓 must be scaled by the square root of the inverse of √π/(2𝑎)}, so
(6.34) 𝜓((𝑥) = √[1/{√π/(2𝑎)}]𝑒-2𝑎𝑥2𝑒𝑖𝑘𝑥 = (2𝑎/π)1/4𝑒-2𝑎𝑥2𝑒𝑖𝑘𝑥.
This function is normalized to give an all-space probability of one.
Example 6.4 Determine the probability of finding a particle at a given location if the particle's wavefunction is defined as
𝜓((𝑥) = (0.2/π)1/4 𝑒-0.1𝑥2 𝑒𝑖𝑘𝑥.
𝜓*((𝑥)𝜓((𝑥) = [(0.2/π)1/4 𝑒-0.1𝑥2 𝑒-𝑖𝑘𝑥][(0.2/π)1/4 𝑒-0.1𝑥2 𝑒𝑖𝑘𝑥] = (0.2/π)1/2 𝑒-0.2𝑥2,
which is a Gaussian distribution, as shown in Fig. 6.9.
To find probability of the particle with this wavefunction being located in a particular spot, we have to integrate the density around that place. In this example the likelihood of finding the particle at 𝑥 = 1, give or take 0.1 m is
𝓟(1 ∓ 0.1) = (0.2/π)1/2∫0.91.1𝑒-0.2𝑥2 𝑑𝑥 = 0.041, [Re Wolframalpha]
or 4.1%. We can check the normalization of this function by integrating over all space:
𝓟all space = (0.2/π)1/2∫-∞ ∞𝑒-0.2𝑥2𝑑𝑥 = 1. [Re Wolframalpha]
If we encounter other wave functions that aren't normalized then we may write the waveform with a multiplicative factor 𝛢 out front, we can set the integral over all space of probability density equal to one and solve for 𝛢.
Example 6.5 Normalize the triangular-pulse wavefunction in Fig. 6.10.
The equation for this triangular pulse can be written as
⌈ 𝛢𝑥 0 ≤ 𝑥 ≤ 0.5,
𝜓((𝑥) =┃𝛢(1-𝑥) 0.5 ≤ 𝑥 ≤ 1,
⌊ 0 else,
which can be plugged into the probability density integral:
𝓟all space = 1 = ∫-∞∞𝜓*(𝑥)𝜓(𝑥)𝑑𝑥. Thus
1 = ∫00.5(𝛢*𝑥)(𝛢𝑥)𝑑𝑥 + ∫0.51(𝛢*(1-𝑥))(𝛢(1-𝑥))𝑑𝑥, and pulling out 𝛢*𝛢 from each integral leaves
1 = 𝛢*𝛢 {∫00.5𝑥2𝑑𝑥 + ∫00.5(1 - 𝑥)2𝑑𝑥} = 𝛢*𝛢 (1/24 + 1/24). [Re Wolframalpha]
Here all factors are real, so 𝛢*𝛢 = 𝛢2. Solving for the normalization constant gives
1 = 𝛢2(1/24 + 1/24), 𝛢 = √12.
Fig. 6.11 shows the probability density before and after normalization. Note that the shape of the normalized probability density haven't changed from non-normalized one: only its scale has changed.
Additionally it's important that we also understand the wavenumber (and momentum) range of those waveform. Using the Fourier synthesis approach, we can construct a spatially limited wavefunction from a single wavelength function 𝑒𝑖𝑘0𝑥 by adding in other single-wavelength function in just the right proportion to cause the amplitude of the combined function to roll off over distance at the desired rate.
If we attempt to do this using a discrete set of wavefunctions 𝜓n and represent the amplitude coefficient of each component waveform as 𝜙n, the combined waveform will be
(6.35) 𝜓((𝑥) = ∑n 𝜓n = [1/√(2π)]∑n 𝜙n𝑒𝑖𝑘𝑥.
The reason for including the scaling factor of 1/√(2π) will be made clear below. If we hope to construct a wavefunction with a single region of large amplitude, the wavenumber difference between the component wavefunctions must be infinitesimally small, and the discrete sum must become an integral.
(6.36) 𝜓(𝑥) = [1/√(2π)] ∫-∞∞ 𝜙(𝑘)𝑒𝑖𝑘𝑥 𝑑𝑘,
in which the discrete coefficient 𝜙n have been replaced by 𝜙(𝑘), a continuous function that determines the amount of each wavenumber component that gets added to the mix.
We may recall Eq. (3.34) which is the equation for the inverse Fourier transform. Thus the spatial wavefunction 𝜓(𝑥) and the wavenumber function 𝜙(𝑘) are a Fourier transform pair. That means we can find the wavenumber function through the forward Fourier transform of 𝜓(𝑥):(1)
(6.37) 𝜙(𝑘) = [1/√(2π)] ∫-∞∞ 𝜓(𝑥)𝑒-𝑖𝑘𝑥 𝑑𝑥,
The Fourier-transform relationship between 𝜓(𝑥) and 𝜙(𝑘) has powerful implications like all conjugate-variable pairs, these functions obey the uncertainty principle, and that help us determine the wavenumber content of a given spatial wavefunction.
To see how that works, consider a general Gaussian envelope function of width 𝜊x. That function can be written as
(6.38) 𝑔(𝑥) = 𝑒-𝑥2/(2𝜊x2).
this is essentially the same envelope function in Eq. (6.33) and 𝑎 = 1/(2𝜊𝑥2), where 𝜊𝑥 is the standard deviation of Gaussian wavefunction. Multiplying this envelope function by interior, single-wavenumber oscillating function 𝑓(𝑥) = 𝑒𝑖𝑘0𝑥 and normalizing produces the waveform. That is Eq. (6.34) with 𝑎 = 1/(2𝜊𝑥2:
(6.39) 𝜓(𝑥) = (1/π𝜊𝑥2)1/4 𝑒-𝑥2/(2𝜊𝑥2)𝑒𝑖𝑘0𝑥.
That Fourier transform is
𝜙(𝑘) = [1/√(2π)] ∫-∞∞ 𝜓(𝑥)𝑒-𝑖𝑘𝑥 𝑑𝑥 = [1/√(2π)](1/π𝜊x2)1/4 ∫-∞∞ 𝑒-𝑥2/(2𝜊𝑥2)𝑒𝑖𝑘0𝑥𝑒-𝑖𝑘0𝑥 𝑑𝑥
So the wavenumber (and momentum) distribution is(2)
(6.40) 𝜙(𝑘) = (𝜊x2/π)1/4 𝑒(𝜊𝑥2/2)(𝑘0-𝑘)2.
This is a Gaussian distribution around 𝑘0 width 𝜊𝑘 = 1/𝜊𝑥. And, the spread in those values depends on how much the packet spreads in space, as expected.
Detailed analysis of uncertainty in position shows that for Gaussian wavevpacket with standard deviation 𝜊𝑥, the position uncertainty is 𝛥𝑥 = 𝜊𝑥/√(2π) and the wavenumber uncertainty is 𝛥𝑘 = 𝜊𝑘/√(2π). And since 𝜊𝑥 =1/𝜊𝑘, the product of the uncertainties in position and wavenumber is
(6.41) 𝛥𝑥𝛥𝑘 = [𝜊𝑥/√(2π)][𝜊𝑘/√(2π)] = [𝜊𝑥/√(2π)][1/𝜊𝑥√(2π)] = 1/2.
Likewise, the product of uncertainties in 𝑥 and 𝑝 is (since 𝑝 = ℏ𝑘)
(6.42) 𝛥𝑥𝛥𝑝 = [𝜊𝑥/√(2π)][𝜊𝑝/√(2π)] = [𝜊𝑥/√(2π)][ℏ𝜊𝑘/√(2π)] = [𝜊𝑥/√(2π)][ℏ/𝜊𝑥√(2π)] = ℏ/2.
This is known as"Heisenberg's uncertainty principle" it's a version of the general uncertainty between conjugate variables discussed in Chapter 3.
If we measure the position of a given particle and then measure its momentum at a later time, we can certainly measure a precise value for each. So there's a better way think about Heisenberg's uncertainty principle.
Imagine that we have a large number of identical particles, all in the same state (so they have the same wavefunction). If the spread positions of these "ensemble" of particles is small, measuring the positions of all of the particles will return very similar values. However, if we measure the momentum of each of these particles, the measured momenta will be very different from one another. That's because particles with position have many contributing momentum states {waves with different wavenumbers), and the measurement process cause the wavefunction to "collapse" randomly to one of those states. Conversely, if the spread in position among the particles is large, then there are few contributing momentum states, and the measured values of momentum will be very similar.
The final aspect of quantum waves we'll consider is the time evolution of the wavefunction of a free particle. To do that, we'll have to put the time term back into the spatially limited wavefunction. At time 𝑡 = 0, the wavefunction 𝛹(𝑥, 0) for Gaussian wave packet can be written as
(6.43) 𝛹(𝑥, 0) = 1/(π𝜊𝑥2) 𝑒𝑖𝑘0𝑥𝑒-𝑥2/(2𝜊𝑥2).
in which 𝜊𝑥 is the standard deviation of Gaussian position envelope. At time 𝑡, this wavefunction is
(6.44) 𝛹(𝑥, 𝑡) = [1/√(2π)] ∫-∞∞ 𝜙(𝑘) 𝑒𝑖[𝑘𝑥-𝜔(𝑘)𝑡] 𝑑𝑘,
in which 𝜙(𝑘) is the wavenumber function that is the Fourier transform of the position function and we've written 𝜔(𝑘) to remind that 𝜔 depends on 𝑘. so the 𝜔(𝑘) = ℏ𝑘2/(2𝑚). Now inserting 𝜙(𝑘) Eq. (6.40) for a Gaussian wavepacket into the expression for 𝛹(𝑥, 𝑡) gives
𝛹(𝑥, 𝑡) = [𝜊𝑥2/(4π3)]1/4 ∫-∞∞ 𝑒(𝜊𝑥2/2)(𝑘0-𝑘)2 𝑒𝑖[𝑘𝑥-𝜔(𝑘)𝑡] 𝑑𝑘,
so the wavefunction is consequently.(3)
(6.45) 𝛹(𝑥, 𝑡) = [𝜊𝑥2/(4π3)]1/4 exp[𝑖(𝑘0𝑥 - 𝜔0𝑡)] [π/{𝜊𝑥2/2 + 𝑖ℏ𝑡/(2𝑚)}]1/2 exp[-(𝑥 - ℏ𝑘0𝑡/𝑚)2/4(𝜊𝑥2/2 + 𝑖ℏ𝑡/(2𝑚)].
This expression for 𝛹(𝑥, 𝑡) looks quite complicate, programs such as Mathematica, MATLAB and Octave help us explore the behavior of the wavefunction over time. For example, if we choose a particle with the mass of a proton (1.67 × 10-27 kg) at a speed of 4 mm/s, the particle's de Broglie wavelength is just under 100 microns. Forming a Gaussian wave packet with a standard deviation of 250 microns results in the wavefunction in Fig. 6.12.
In this figure, the wavefunction is shown at times of 𝑡 = 0, 1, and 2 seconds over a spatial interval about 10 mm. The particles dominant wavelength is approximately 100 microns, and there are about 2.5 cycles on either side of the central maximum within the standard deviation at time 𝑡 = 0. Each second, the wave packet propagates 4 mm, so the group velocity of the packet equals the particles's speed, as expected.
The component waves that make up the wave packet all have slightly different velocities, but those velocities are about half the group velocity of the packet. To see the reason, consider that the dispersion relationship for de Broglie waves is (also see eq. (6.14) when 𝑉 = 0)
(6.46) 𝜔(𝑘) = [ℏ/(2𝑚)]𝑘2,
so the packet's group velocity 𝑑𝜔/𝑑𝑘 is
(6.47) 𝑣𝑔 = (𝑑𝜔/𝑑𝑘) = ℏ𝑘/𝑚,
which is the classical particle speed. Recall also that the phase velocity is 𝜔/𝑘, which is
(6.48) 𝑣𝑝 = 𝜔/𝑘 = ℏ𝑘/(2𝑚).
This is half the wave packet 's group velocity, and half the particles's speed.
Figure 6.13 shows the probability density of the wave packet moving through space as time passes. As we can see both the plot of 𝛹(𝑥, 𝑡) and the plot of the probability density. the wave packet isn't just moving, it's also spreading out as time passes. As explained Section 3.4 0f Chapter 3. dispersion occurs whenever the component waves that make up a wave packet travel with different speeds. Given that the quantum dispersion relationship is not linear with respect to 𝑘, quantum objects are dispersive - the different speeds of the components of the wave packet cause the packet to spread out in time.
All of the matter waves we've seen in this chapter have been for free particles in the regions constant energy (which we set to zero): these all have 𝑒𝑖𝑘𝑥 as their basic functions. As mentioned in Chapter 4, waves have non-sinusoidal basis functions in an inhomogeneous string. This is also true for matter waves in regions of non-constant potential energy. And, we may study on them further in the same author's other textbook.(4)
(1) This is why we included the factor of 1/√(2π) to Eq.(6.36)
(2) (3) For this complicate integral, we can calculate with Wolframalpha or refer to textbook's online solution.
(4) D. Fleisch A Student's Guide to Schrödinger Equation (Cambridge University Press 2020)
* Textbook: D. Fleisch & J. Kinnaman A Student's Guide to Waves (Cambridge University Press 2015) |
|
|





































