|
김관석
|
2019-06-03 00:08:56, 조회수 : 866 |
- Download #1 : Tensor_I_2.jpg (47.8 KB), Download : 1

I-7 Tensor의 미분과 적분
a) 7.2 좌표에 대한 미분
함수 𝜙(𝐱)에 대한 좌표에 대한 미분 → ∂𝜙 /∂x𝑖 또는 𝜙,𝑖 <- index notation(지수 표기) [7.2.1]
b) 7.3 Del operator(미분 연산자)
𝛁 = ∂/∂𝐱 = (∂/∂x𝑖) 𝐞𝑖 <- 1차 tensor, Einstein summation convention 이하 동일 [7.3.1,2]
c) 7.4 Gradient(구배)
∘ Scalar field(스칼라장): 𝛁𝜙 = ∂𝜙/∂𝐱 = (∂𝜙/∂x𝑖) 𝐞𝑖 = 𝜙,𝑖 𝐞𝑖 [7.4.1,2]
∘ Vector field(벡터장): 𝛁𝐮 = ∂𝐮/∂𝐱 = (∂u𝑗/∂x𝑖) 𝐞𝑖 ⊗ 𝐞𝑗 <- 2차 tensor [7.4.3]
∘ Conjugate gradient(켤레 구배): 𝐮𝛁 = (∂u𝑖/∂x𝑗) 𝐞𝑖 ⊗ 𝐞𝑗 [7.4.5]
∘ Vector 미분과 Kronecker delta: 𝛁𝐱 = ∂𝐱/∂𝐱 = (∂x𝑗/∂x𝑖) 𝐞𝑖 ⊗ 𝐞𝑗 = 𝐈 = δ𝑖𝑗 𝐞𝑖 ⊗ 𝐞𝑗 [7.4.7-12]
∘ 2차 tensor gradient: 𝛁𝐀 = (∂/∂x𝑖) 𝐞𝑖 ⊗ (A𝑗𝑘 𝐞𝑗 ⊗ 𝐞𝑘) = (∂A𝑗𝑘/∂x𝑖) 𝐞𝑖 ⊗ 𝐞𝑗 ⊗ 𝐞𝑘; ∂A𝑗𝑘/∂x𝑖 = A𝑗𝑘,𝑖 [7.4.18,19]
d) 7.5 Divergence(발산)
∘ Vector divergence: 𝛁 ∙ 𝐮 = (∂/∂𝐱) ∙ 𝐮 = (∂/∂x𝑖) 𝐞𝑖 ∙ u𝑗 𝐞𝑗 = (∂u𝑗/∂x𝑖) 𝐞𝑖 ∙ 𝐞𝑗 = (∂u𝑗/∂xi) δ𝑖𝑗 = ∂u𝑖/∂x𝑖 [7.5.1-3]
∘ 2차 tensor: 𝛁 ∙ 𝐀 = (∂/∂x𝑖) 𝐞𝑖 ∙ A𝑗𝑘 (𝐞𝑗 ⊗ 𝐞𝑘) = (∂A𝑗𝑘/∂x𝑖)(𝐞𝑖 ∙ 𝐞𝑗) 𝐞𝑘 = (∂A𝑗𝑘/∂x𝑖) δ𝑖𝑗 𝐞𝑘 = (∂A𝑖𝑘/∂x𝑖) 𝐞𝑘 [7.5.7-10]
e) 7.6 Laplacian operator(Laplacian 연산자)
𝛁2 = 𝛁 ∙ 𝛁 = (∂/∂x𝑖) 𝐞𝑖 ∙ (∂/∂x𝑗) 𝐞𝑗 = (∂2/∂x𝑗∂x𝑖) 𝐞𝑖 ∙ 𝐞𝑗 = (∂2/∂x𝑗∂x𝑗) δ𝑖𝑗= ∂2/∂x𝑖∂x𝑖 로 정의됩니다. [7.6.1-3]
f) 7.7 Curl(회전)
∘ Vector curl : 𝛁 ⨯ 𝐮 = (∂/∂x𝑖) 𝐞𝑖 ⨯ u𝑗 𝐞𝑗 = (∂u𝑗/∂x𝑖) (𝐞𝑖 ⨯ 𝐞𝑗) = e𝑖𝑗𝑘 u𝑗,𝑖 𝐞𝑘 [7.7.1-2]
= 𝐞1[(∂/∂x2)u3 - (∂/∂x3)u2] - 𝐞2[(∂/∂x1)u3 - (∂/∂x3)u1] + 𝐞3[(∂/∂x1)u2 - (∂/∂x2)u1] [7.7.3]
∘ Vector conjugate curl: 𝐮 ⨯ 𝛁 = u𝑖 𝐞𝑖 ⨯ (∂/∂x𝑗) 𝐞𝑗 = (∂u𝑖/∂x𝑗) (𝐞𝑖 ⨯ 𝐞𝑗) = e𝑖𝑗𝑘 u𝑖,𝑗 𝐞𝑘 [7.7.4-7]
∘ 2차 tensor curl: 𝛁 ⨯ 𝐀 = (∂/∂x𝑖) 𝐞𝑖 ⨯ A𝑗𝑘 (𝐞𝑗 ⊗ 𝐞𝑘) = (∂A𝑗𝑘/∂x𝑖) (𝐞𝑖 ⨯ 𝐞𝑗) 𝐞𝑘 = e𝑖𝑗𝑙 A𝑗𝑘,𝑖 (𝐞𝑙 ⊗ 𝐞𝑘) [7.7.8-12]
g) 7.9 Tensor와 적분
∘ Gradient theorem(구배 정리):
∭v 𝛁 𝜙 𝑑𝑉 = ∬s 𝜙 𝐧 𝑑𝑆 → ∭v 𝜙,𝑖 𝑑𝑉 = ∭v ∂𝜙/∂𝑥𝑖 𝑑𝑉 = ∬s 𝜙𝑛𝑖 𝑑𝑆 <- 𝑛𝑖: 수직인 단위 vector [7.9.1,2]
∘ Divergence theorem(발산 정리):
∭v 𝛁 ∙ 𝐮 𝑑𝑉 = ∬s 𝐮 ∙ 𝐧 𝑑𝑆 → ∭v 𝑢𝑖,𝑖 𝑑𝑉 = ∭v ∂𝑢𝑖/∂𝑥𝑖 𝑑𝑉 = ∬s 𝑢𝑖𝑛𝑖 𝑑𝑆 [7.9.3,4]
∘ Stokes theorem(Stokes 정리):
∬s (𝛁 X 𝐮) ∙ 𝐧 𝑑𝑆 = ∫c 𝐮 ∙ 𝑑𝐶 → ∬s 𝑛𝑖 𝑒𝑖𝑗𝑘 𝑢𝑘,𝑗 𝑑𝑆 = ∬s 𝑛𝑖 𝑒𝑖𝑗𝑘 ∂𝑢𝑘/∂𝑥j 𝑑𝑆 = ∫c 𝑢𝑖 𝑑𝐶𝑖 [7.9.5,6]
h) 7.10 Taylor series(Taylor 급수 전개)
∘ Scala function: 𝑓(𝑥 + 𝛥𝑥) = 𝑓(𝑥 ) + (𝑑𝑓/𝑑𝑥)𝛥𝑥 + (1/2!)(𝑑2𝑓/𝑑𝑥2)(𝛥𝑥)2 + (1/3!)(𝑑3𝑓/𝑑𝑥3)(𝛥𝑥)3 + ∙∙∙ [7.10.1]
∘ Vector function: 𝑓(𝐱 + 𝛥𝐱) = 𝑓(𝑥 ) + (𝑑𝑓/𝑑𝐱) ∙ 𝛥𝐱 + (1/2!)(𝑑2𝑓/𝑑𝐱𝑑𝐱) : 𝛥𝐱 + (1/3!)(𝑑3𝑓/𝑑𝐱𝑑𝐱𝑑𝐱) : 𝛥𝐱 + ∙∙∙ [7.10.3]
I-8 Tensor와 좌표 변환 I
a) 8.2 좌표 변환의 원리 <- 그림 8.1 참조
∘ 기저 벡터의 변환: ē𝑖 = 𝑙𝑖𝑗 𝐞𝑗 = 𝐋 𝐞𝑗 <- 𝐋 = [𝑙𝑖𝑗]: 변환 tensor [8.2.2]
⌈ ēi ⌉ ⌈ 𝑙11 𝑙12 𝑙13 ⌉ ⌈ 𝐞i ⌉
┃ē2┃ = ┃ 𝑙21 𝑙22 𝑙23┃ ┃𝐞2┃ [8.2.3]
⌊ ē3 ⌋ ⌊ 𝑙31 𝑙33 𝑙33 ⌋ ⌊ 𝐞3 ⌋
𝑙𝑖𝑗 ≡ ē𝑖 ∙ 𝐞𝑗 = cos 𝜃𝑖𝑗 <- 𝜃𝑖𝑗: ē𝑖와 𝐞𝑗가 이루고 있는 각도 [8.2.4,5]
∘ Orthogonal(직교) tensor: 변환된 좌표계도 Cartesian 좌표계일 경우
𝐞𝑖 ∙ 𝐞𝑗 = δ𝑖𝑗, ē𝑖 ∙ ē𝑗 = δ𝑖𝑗, 𝑙𝑖𝑘 𝐞𝑘 ∙ ē𝑗 = δ𝑖𝑗, (∵ ē𝑖 = 𝑙𝑖𝑘 𝐞𝑘, 𝐞𝑘 ∙ ē𝑗 = 𝑙𝑖𝑘), 𝑙𝑖𝑘 𝑙𝑘𝑗 = δ𝑖𝑗 [8.2.7-10]
∴ 𝐋 ∙ 𝐋T = 𝐋T ∙ 𝐋 = 𝐈 → ※ 중요 𝐋-1 = 𝐋T 이면 orthogonal(직교) tensor라고 정의합니다. [8.2.11,12]
∘ 좌표계의 역변환: 𝑙𝑖𝑘 ē𝑖 = 𝑙𝑖𝑘 𝑙𝑖𝑗 𝐞𝑗 = δ𝑗𝑘 𝐞𝑗, ∴ 𝐞i = 𝑙𝑗𝑖 ē𝑗 = 𝐋T ē𝑗 [8.2.13,14]
b) 8.3 좌표 회전 변환:
먼저 z축에 대한 반시계 방향 𝜃 만큼 회전 변환을 수행하는 경우를 예를 들어 설명합니다.
𝐮 = u𝑖 𝐞𝑖에서 ū = ū𝑖 ē𝑖로 변환 <- ū = 𝐋 𝐮, ū𝑖 = 𝑙𝑖𝑗 u𝑖, 𝐋 = 𝑙𝑖𝑗 [8.3.1- 5]
⌈ ū1 ⌉ ⌈ cos 𝜃 sin 𝜃 0 ⌉ ⌈ u1 ⌉
┃ū2┃ = ┃-sin 𝜃 cos 𝜃 0 ┃ ┃u2┃
⌊ ū3 ⌋ ⌊ 0 0 1 ⌋ ⌊ u3 ⌋
∘ x, y, z축에 대한 회전 변환 tensor들은 각각 다음과 같습니다.
[ 𝑙𝑖𝑗]x = [ 𝑙𝑖𝑗]y = [ 𝑙𝑖𝑗]z =
⌈ 1 0 0 ⌉ ⌈ cos 𝜃 0 -sin 𝜃 ⌉ ⌈ cos 𝜃 sin 𝜃 0 ⌉
┃ 0 cos 𝜃 sin 𝜃 ┃ ┃ 0 1 0 ┃ ┃ -sin 𝜃 cos 𝜃 0 ┃ [8.3.6-8]
⌊ 0 -sin 𝜃 cos 𝜃 ⌋ ⌊ sin 𝜃 0 cos 𝜃 ⌋ ⌊ 0 0 1 ⌋
∘ proper orthogonal translation(적합 직교 변환): det [𝑙𝑖𝑗] = 1, 오른손 좌표계로 변환함.
improper orthogonal translation(부적합 직교 변환): det [𝑙𝑖𝑗] = -1, 왼손 좌표계로 변환함.
∘ 2차 tensor의 변환식
임의의 tensor 𝐀 = A𝑖𝑗 𝐞𝑖 ⊗ 𝐞𝑗 = Ā𝑖𝑗 ē𝑖 ⊗ ē𝑗 [8.4.1]
𝐞𝑖 = 𝑙𝑘𝑖 ē𝑘, 𝐞𝑗 = 𝑙𝑖𝑗 ē𝑙. ∴ A𝑖𝑗 𝐞𝑖 ⊗ 𝐞𝑗 = 𝑙𝑘𝑖𝑙𝑙𝑗 A𝑖𝑗 ē𝑘 ⊗ ē𝑙 = 𝑙𝑖𝑘𝑙𝑗𝑙 A𝑘𝑙 ē𝑖 ⊗ ē𝑗 <- 𝑖 ⇄ 𝑘, 𝑗 ⇄ 𝑙 지수 조정 [8.4.2,3]
∴ Ā𝑖𝑗 = 𝑙𝑖𝑘𝑙𝑗𝑙 A𝑘𝑙 [8.4.4]
c) 8.5 변환 tensor의 성질 <- ※ 좌표에 의한 미분
x̄𝑖 = 𝑙𝑖𝑗 x𝑗, 좌표 x𝑗로 양변을 미분하면, ∂x̄𝑖/∂x𝑗 = 𝑙𝑖𝑗 [8.5.1,2]
역변환의 경우도 x𝑗 = 𝑙𝑗𝑖 ̄x𝑖, ̄x𝑖로 양변을 미분하면, ∂x𝑗/∂x̄𝑖 = 𝑙𝑗𝑖 [8.5.3,4]
∴ ū𝑖 = 𝑙𝑖𝑗 u𝑗 = ∂x̄𝑖/∂x𝑗 u𝑗, u𝑗 = 𝑙𝑗𝑖 ū𝑗 = ∂x𝑖/∂x̄𝑗 ū𝑖; ∴ ē𝑖 = 𝑙𝑖𝑗 𝐞𝑗 = ∂x̄𝑖/∂x𝑗 𝐞𝑗, 𝐞𝑖 = 𝑙𝑗𝑖 ē𝑗 = ∂x𝑖/∂x̄𝑗 ē𝑗 [8.5.5-8]
∴ Ā𝑖𝑗 = 𝑙𝑖𝑘𝑙𝑗𝑙 A𝑘𝑙 = (∂x̄𝑖/∂x𝑘)(∂x̄𝑗/∂x𝑙) A𝑘𝑙, A𝑖𝑗 = 𝑙𝑘𝑖𝑙𝑙𝑗 Ā𝑘𝑙 = (∂x𝑖/∂x̄𝑘)(∂x𝑗/∂x̄𝑙) Ā𝑘𝑙 [8.5.9,10]
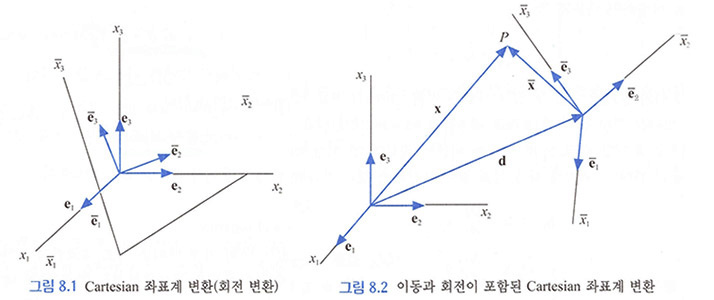
d) 8.6 이동 및 반사 변환 <- 그림 8.2 참조
∘ 회전-이동 변환: x̄𝑖 = 𝑙𝑖𝑗 xj - 𝑑𝑖, 양변을 미분하면, ∂x̄𝑖/∂x𝑗= 𝑙𝑖𝑗 [8.6.1,2]
∘ 반사 변환: [𝑙𝑖𝑗] = <- ex) y-z 평면에 대한 반사 변환; det [𝑙𝑖𝑗] = -1 <- 부적합 직교 변환 [8.6.3]
⌈ -1 0 0 ⌉
┃ 0 1 0 ┃
⌊ 0 0 1 ⌋
e) 8.7 Jacobian <- ※ 좌표 변환의 determinant 決定素
𝑱 = <- x̄ = x̄ (x1, x2, x3)으로 주어진 경우
∣ ∂x̄1/∂x1 ∂x̄1/∂x2 ∂x̄1/∂x3 ∣ ⌈ 𝑱 ≠ 0 : 좌표 변환 가능함.
∣ ∂x̄2/∂x1 ∂x̄2/∂x2 ∂x̄2/∂x3 ∣ <- ┃ 𝑱 > 0 : 오른손 좌표계인 경우 [8.7.1]
∣ ∂x̄3/∂x1 ∂x̄3/∂x2 ∂x̄3/∂x3 ∣ ⌊ 𝑱 < 0 : 왼손 좌표계인 경우
f) 8.8 isotropic(등방) tensor
회전 변환 시에 성분의 변화가 없는 tensor를 지칭 → scalar, 𝟎 vector (1차 tensor 중 유일함)
2차 tensor Ā𝑖𝑗 = 𝑙𝑖𝑘𝑙𝑗𝑙 A𝑘𝑙 회전 변환식에서, Ā𝑖𝑗 = A𝑖𝑗 성분 불변의 조건이 만족되어야 함.
g) 8.9 미분 성분의 좌표 변환
∘ Gradient 좌표 변환: scalar field 𝜙̄ = 𝜙 (∵ scalar는 좌표 변환에 불변)
𝛁𝜙̄ = ∂𝜙̄ /∂x̄𝑖 ē𝑖 = ∂𝜙/∂x̄𝑖 ē𝑖; ∂𝜙/∂x̄𝑖 = (∂𝜙/∂x𝑘)(∂x𝑘/∂x̄𝑙) = 𝑙𝑖𝑘 (∂𝜙/∂x𝑘) [8.9.1,2]
𝛁𝜙̄ = ∂𝜙̄ /∂x̄𝑖 ē𝑖 = 𝑙𝑖𝑘 (∂𝜙/∂x𝑘) ē𝑖 [8.9.3]
∘ Divergence 좌표 변환: ※ 좌표계와 무관하게 불변
𝛁 ∙ 𝐮 = ∂/∂x̄𝑖 ē𝑖 ∙ ū𝑗 ē𝑗 = ∂ū𝑖/∂x̄𝑖 = ∂/∂x𝑘 (𝑙𝑖𝑗u𝑗) ∂x𝑘/∂x̄ 𝑖 = 𝑙𝑖𝑗𝑙𝑖𝑘 ∂u𝑗/∂x𝑘 = ∂u𝑘/∂x𝑘 <- 직교 변환 𝑙𝑖𝑗𝑙𝑖𝑘= 𝛿𝑗𝑘 [8.9.6-8]
∘ Curl 좌표 변환: ※ 순환 기호는 회전에 등방성 → 𝑒̄ 𝑖𝑗𝑘 = 𝑒𝑖𝑗𝑘
𝛁 ⨯ 𝐮 = 𝑒̄ 𝑖𝑗𝑘 ∂ū𝑗/∂x̄𝑖 ē𝑘 = 𝑒𝑖𝑗𝑘 (∂𝑗/∂xp)(𝑙𝑗𝑞u𝑞)(∂x𝑝/∂x̄𝑖) ē𝑘 = 𝑒𝑖𝑗𝑘 𝑙𝑗𝑞 𝑙𝑖𝑝 (∂u𝑞/∂x𝑝) ē𝑘 [8.9.9]
∘ 시간의 미분: vector 변환 법칙을 만족
속도 𝐯 = 𝑑𝐫/𝑑𝑡 (𝐫은 위치 vector, 𝑡는 시간), 𝑣̄i = 𝑑𝑟̄𝑖/𝑑𝑡 = (𝑑/𝑑𝑡)(𝑙𝑖𝑗𝑟j) = 𝑙𝑖𝑗 (𝑑𝑟𝑗/𝑑𝑡) = 𝑙𝑖𝑗 𝑣𝑖 [8.9.10,11] |
|
|





































