|
김관석
|
2019-06-03 21:39:43, 조회수 : 940 |
- Download #1 : Tesor_II_1.jpg (49.2 KB), Download : 5

II-1 일반 좌표계와 Tensor
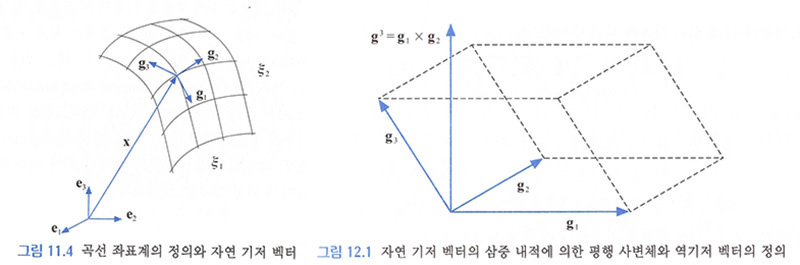
a) 11.1 General coordinate(일반 좌표계) <- 그림 11.4 참조
∘ Cartesian coordinates(좌표계): 𝐱1= x, 𝐱2= y, 𝐱3= z, 𝐮 = 𝑢1𝐞1 + 𝑢2𝐞2 + 𝑢3𝐞3
∘ Cylindrical coordinates(원통 좌표계): 𝜉1= 𝑟, ξ2= 𝜃, 𝜉3= 𝑧, 𝐱1= 𝑟 cos𝜃, 𝐱2 = 𝑟 sin𝜃, x3 = 𝑧
∘ Sphrical coordinates(구 좌표계): 𝜉1= 𝜌, 𝜉2= 𝜃, 𝜉3= 𝜙, 𝐱1= 𝜌 sin𝜃 cos𝜙, 𝐱2= 𝜌 sin𝜃 sin𝜙, 𝐱3= 𝜌 cos𝜃
∘ Curviinear coordinates(곡선 좌표계) → general coordinate(일반 좌표계)로 지칭되기도 함.
다른 좌표계들과 달리 특정의 reference point(기준점)이 없으며 Cartesian 좌표계의 원점에 대한 상대적인 위치에서 정해집니다.
curvilinear 좌표계는 global coordinate(광역 죄표계)인 Cartesian 좌표계와 달리 local coordinate(국소 좌표계)라고 부릅니다.
위 그림에서 보듯이 Cartesian 좌표계에서 임의 거리만큼 떨어진 한점까지를 잇는 vector를 위치 vector 𝐱 라고 표기합니다.
이 점에서 curvilinear 좌표계는 좌표계의 components(성분)에 따른 곡면을 가지게 됩니다.
b) 11.2 일반 좌표계(곡선 좌표계)에서의 표기법
∘ 일반 좌표계의 vector 𝐮 = 𝑢𝑖 𝐠𝑖 = 𝑢𝑖 𝐠𝑖 <- ※ 일반 tensor의 중복지수는 반드시 위와 아래로 교차하도록 해야 합니다. [11.2.2,5]
𝐮 = 𝑢𝑖 𝐠𝑖 = 𝑢1𝐠𝑖 + 𝑢2𝐠2 + 𝑢3𝐠3 <- 𝑢𝑖: contravariant component(반변 성분), 𝐠𝑖: natural basis(자연 기저) vector [11.2.3]
𝐮 = 𝑢𝑖 𝐠𝑖 = 𝑢1𝐠1 + 𝑢2𝐠2 + 𝑢3𝐠3 <- 𝑢𝑖: covariant component(공변 성분), 𝐠𝑖: reciprocal basis(역기저) vector [11.2.4]
∘ 2차 tensor 표기법: 다음의 4가지로 표현될 수 있습니다.
𝐀 = 𝐴𝑖𝑗 𝐠𝑖 ⊗ 𝐠𝑗 = 𝐴𝑖𝑗 𝐠𝑖 ⊗ 𝐠𝑗 = 𝐴𝑖,𝑗 𝐠𝑖 ⊗ 𝐠𝑗 = 𝐴𝑖,𝑗 𝐠𝑖⊗ 𝐠𝑗 <- contravant(반변), covariant(공변), mixed(혼합) 성분 [11.2.6-8]
c) 11.3 General(일반) tensor의 성질
∘ Tanspose(전치):
symmetric tensor 𝐀T = (𝐴𝑖𝑗)T 𝐠𝑖 ⊗ 𝐠j = 𝐴𝑗𝑖 𝐠𝑖 ⊗ 𝐠j = 𝐴𝑖𝑗 𝐠j ⊗ 𝐠𝑖, (𝐴𝑖𝑗)T = 𝐴𝑗𝑖, (𝐴𝑖𝑗)T = 𝐴𝑗𝑖, (𝐴𝑖,j)T = 𝐴j,𝑖 [11.3.1,2]
symmetric tensor: If 𝐀T = 𝐀, then 𝐀: sym𝐀 <- square matrix
skew-symetric(반대칭) tensor: If 𝐀T = -𝐀, then 𝐀: skew𝐀 <- square matrix [11.3.3]
𝐀 = sym𝐀 + skew𝐀, sym𝐀 = 1/2 (𝐀 + 𝐀T), skew𝐀 = 1/2 (𝐀 - 𝐀T) <- Toeplitz decomposition 'Symmetric matrix'[link]
∘ 덧셈과 뺄셈: 동일한 기저(basis)를 갖는 성분(component) 간에 가능
ex1) 𝐀 - 𝐁 = (𝐴𝑖𝑗 - 𝐵𝑖𝑗) 𝐠𝑖 ⊗ 𝐠𝑗 = 𝑇𝑖𝑗 = 𝐓, ex2) 𝐀 - 𝐁 = (𝐴𝑖,𝑗 - 𝐵𝑖,𝑗) 𝐠𝑖 ⊗ 𝐠𝑗 = 𝑇𝑖,𝑗 = 𝐓 [11.4.4,5]
d) 11.5 General tensor의 유용성: ※ 좌표계에 무관한 수식 표현이 가능하므로, Einstein에 의해 일반 상대성 원리(GR)에 활용되었음.
Cartesian 좌표계에서: ex) velocity 𝐯 = 𝑣𝑖𝐞𝑖, 𝑣𝑖 = 𝑎𝑖𝑡, 𝑣𝑖𝐞𝑖 = 𝑎𝑖𝐞𝑖𝑡 ∴ 𝐯 = 𝐚𝑡 <- 𝐚: acceleration, 𝑡: time [11.5.1,4]
General 좌표계에서: ex) velocity 𝐯 = 𝑣𝑖𝐠𝑖, 𝑣𝑖 = 𝑎𝑖𝑡, 𝑣𝑖𝐠𝑖 = 𝑎𝑖𝐠𝑖𝑡 ∴ 𝐯 = 𝐚𝑡 <- 𝐚: acceleration, 𝑡: time [11.5.2,5]
II-2 일반 좌표계에서의 연산
a) 12.1 Inner product(내적)
∘ Metric tensor: 𝑔𝑖𝑗 ≡ 𝐠𝑖 ∙ 𝐠𝑗; If 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗, then 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 𝑔𝑖𝑗 [12.1.6]
metric tensor [𝑔𝑖𝑗] =
⌈ 𝑔11 𝑔12 𝑔13 ⌉
┃ 𝑔21 𝑔22 𝑔23┃ (𝑖,𝑗 = 1,2,3) [12.1.7]
⌊ 𝑔31 𝑔32 𝑔33 ⌋
∘ Kronecker delta: 𝛿𝑖𝑗 ≡ 𝐠𝑖 ∙ 𝐠𝑗 = {0 (𝑖≠𝑗); 1 (𝑖=𝑗)}; If 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠j, then 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 𝛿𝑖𝑗 = 𝑎𝑖𝑏i <- index 교환 (j→i of 𝑏) [12.1.11,12]
∘ Reciprocal(역) metric tensor: 𝑔𝑖𝑗 ≡ 𝐠𝑖 ∙ 𝐠𝑗; If 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗, then 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏j 𝑔𝑖𝑗 [12.1.13,14]
∘ Identity(단위) tensor: 𝐈 = 𝛿𝑖𝑗 𝐠𝑖 ⊗ 𝐠𝑗 = 𝐠𝑖 ⊗ 𝐠𝑖, 𝐈 = 𝐈T = 𝛿𝑗𝑖 𝐠𝑖 ⊗ 𝐠𝑗 = 𝐠𝑗 ⊗ 𝐠𝑗 ∴ 𝐈 = 𝐠𝑖 ⊗ 𝐠𝑖 = 𝐠𝑖 ⊗ 𝐠𝑖 [12.1.15-17]
∘ Index 기호∙위치 바꾸기: ※ metric tensor/reciprocal metric tensor는 근접해 있는 index의 기호와 위치를 동시에 바꿈.
𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗 = 𝑎𝑖𝑏𝑗 𝑔𝑖𝑗 = 𝑎𝑖𝑏i, 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗 = 𝑎𝑖𝑏𝑗 𝛿𝑗𝑖 = 𝑎𝑖𝑏i, 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗 = 𝑎𝑖𝑏𝑗 𝛿𝑖𝑗 = 𝑎𝑖𝑏𝑖, 𝑎𝑖𝑏𝑗 𝐠𝑖 ∙ 𝐠𝑗 = 𝑎𝑖𝑏𝑗 𝑔𝑖𝑗 = 𝑎𝑖𝑏𝑖, 𝐚 ∙ 𝐛 = 𝑎𝑖𝑏𝑗 = 𝑎𝑖𝑏𝑗 [12.1.24-28]
b) 12.2 Inner product(내적) 응용
∘ Basis(기저) vector의 변환: 𝐠𝑖 = 𝑔𝑖𝑗 𝐠𝑗, 𝐠𝑖 = 𝑔𝑖𝑗 𝐠𝑗 [12.2.1,2]
∘ Metric tensor 관계식: [𝑔𝑖𝑗] = [𝑔𝑖𝑗]-1 ∵ 𝑔𝑖𝑗 ∙ 𝑔𝑖𝑗 = 𝐠𝑖 ∙ 𝐠𝑗 ∙ 𝐠𝑖 ∙ 𝐠𝑗 = 𝐠𝑖 ∙ 𝐠𝑗 ∙ 𝐠𝑗 ∙ 𝐠𝑖 = 𝛿𝑖𝑗 𝛿𝑗𝑖 = 𝐈 [12.2.6-8]
∘ Trace(대각합): tr𝐀 = 𝐀 : 𝐈 ≡ 𝐴𝑖,𝑖, tr(𝐀2) = tr(𝐀 ∙ 𝐀) = 𝐀 : 𝐀 = 𝐴𝑖,𝑗𝐴j,𝑖, (tr𝐀)2 = tr(𝐀) tr(𝐀) = 𝐴𝑖,𝑖 𝐴𝑗,𝑗 [12.2.12-14]
∘ Vector의 크기: 𝐧 = 𝑛𝑖 𝐠𝑖의 크기 → ∥𝐧∥= √ (𝐧 ∙ 𝐧) = √ (𝑛𝑖 𝐠𝑖 ∙ 𝑛𝑗 𝐠𝑗) = √ (𝑛𝑖𝑛𝑗𝑔𝑖𝑗) = √ (𝑛i𝑛𝑗), ∴ ∥𝐧∥= √ (𝐧 ∙ 𝐧) = √ (𝑛i𝑛i) [12.2.16-18]
∘ Basis(기저) vector의 크기: ∥𝐠𝑖∥= √ (𝐠𝑖̄ ∙ 𝐠𝑖̄) = √ 𝑔𝑖̄𝑖̄, ∥𝐠𝑖∥= √ (𝐠𝑖̄ ∙ 𝐠𝑖̄) = √ 𝑔𝑖̄𝑖̄ <- ※ 𝑖̄ : 중복지수(dummy index) 미적용 표기임. [12.2.19-24]
ex) 원통 좌표계의 자연 기저 vector 크기∥𝐠𝑖∥를 구하시오. ◂
∥𝐠1∥= √ (𝐠1 ∙ 𝐠1) = √ 𝑔11, ∥𝐠2∥= √ (𝐠2 ∙ 𝐠2) = √ 𝑔22, ∥𝐠3∥= √ (𝐠3 ∙ 𝐠3) = √ 𝑔33 ▮ [12.2.25]
c) 12.3 Tensor component(성분) 변환
∘ Tensor 성분 구하기: 원하는 방향의 basis vector를 tensor에 dot product를 함. <- 1차 tensor: 1회, 2차 tensor: 2회
ex1) 𝐮 ∙ 𝐠𝑗 = 𝑢𝑖 𝐠𝑖 ∙ 𝐠𝑗 = 𝑢𝑖𝛿𝑖𝑗 = 𝑢𝑗, ex2) 𝐠𝑘 ∙ 𝐀 ∙ 𝐠𝑙 = 𝐠𝑘 ∙ (𝐴𝑖𝑗 𝐠𝑖 ⊗ 𝐠𝑗) ∙ 𝐠𝑙 = 𝐴𝑖𝑗 (𝐠𝑘 ∙ 𝐠𝑖)(𝐠𝑗 ∙ 𝐠𝑙) = 𝐴𝑖𝑗 𝑔𝑘𝑖 𝑔𝑗𝑙 = 𝐴𝑘𝑙 [12.3.1,3]
∘ Tensor 구성하기: tensor의 성분아 알려져 있을 때는 basis vector를 곱하여 tensor를 회복할 수 있습니다.
ex1) 𝑢𝑗 (= 𝐮 ∙ 𝐠𝑗)를 알면, 𝑢j 𝐠𝑗 = 𝐮; ex2) 𝑢𝑗 (= 𝐮 ∙ 𝐠𝑗)를 알면, 𝑢𝑗 𝐠𝑗 = 𝐮 [12.3.15,16].
∘ 12.4 Tensor 성분 변환 절차: 𝐚 = 𝑢𝑖 𝐠𝑖 <- contavariant 성분과 자연 기저 vector가 주어질 경우
1) metric tensor 구하기: ; 𝑔𝑖𝑗 = 𝐠𝑖 ∙ 𝐠𝑗
ex) 원통 좌표계 (𝑟, 𝜃, 𝑧)에서 x = 𝑟 cos 𝜃, y = 𝑟 sin 𝜃, z = 𝑧 일 때 해당 metric tensor 𝑔𝑖𝑗를 구하시오. ◂
⌈ 𝐠1 ⌉ ⌈ cos𝜃 sin𝜃 0 ⌉ ⌈ 𝐞1 ⌉
┃𝐠2┃ = ┃ -𝑟 sin 𝜃 𝑟 cos𝜃 0 ┃ ┃𝐞2┃ [12.1.8]
⌊ 𝐠3 ⌋ ⌊ 0 0 1 ⌋ ⌊ 𝐞3 ⌋
∴ 𝐠1 = cos𝜃 𝐞1 + sin𝜃 𝐞2, 𝐠2 = -𝑟 sin𝜃 𝐞1 + 𝑟 cos𝜃 𝐞2, 𝐠3 = 𝐞3
𝑔11 = 𝐠1 ∙ 𝐠1 = (cos𝜃 𝐞1 + sin𝜃 𝐞2) ∙ (cos𝜃 𝐞1 + sin𝜃 𝐞2) = 1, 같은 방식으로 계산을 계속한 결과는,
metric tensor [𝑔𝑖𝑗] =
⌈ 1 0 0 ⌉
┃ 0 𝑟2 0┃ ▮ [12.1.9]
⌊ 0 0 1 ⌋
2) reciproca(역) metric tensor 구하기: 𝑔𝑖𝑗 <- [𝑔𝑖𝑗] = [𝑔𝑖𝑗]-1 관계식으로 부터
ex) 원통 좌표계 (𝑟, 𝜃, 𝑧)의 경우에 역 metric tensor 구하시오. ◂
reciprocal metric tensor [𝑔𝑖𝑗] =
⌈ 1 0 0 ⌉ -1 ⌈ 1 0 0 ⌉
┃0 𝑟2 0┃ = ┃0 1/𝑟2 0┃ ▮ [12.2.9]
⌊ 0 0 1 ⌋ ⌊ 0 0 1 ⌋
3) reciproca(역) 기저 vector 구하기: 𝐠𝑖 = 𝑔𝑖𝑗 𝐠𝑗
ex) 원통 좌표계 (𝑟, 𝜃, 𝑧)의 경우에 역기저 vector 𝐠𝑖를 유도하시오. ◂
𝐠1 = 𝑔11𝐠1 + 𝑔12𝐠2 + 𝑔13𝐠3 = 𝐠1 + 0 + 0 = 𝐠1 ∴ 𝐠1 = cos𝜃 𝐞1 + sin𝜃 𝐞2
𝐠2 = 𝑔21𝐠1 + 𝑔22𝐠2 + 𝑔23𝐠3 = 0 + (1/𝑟2 ) 𝐠2 + 0 + 0 = (1/𝑟2 ) 𝐠2 ∴ 𝐠2 = -(1/𝑟) sin𝜃 𝐞1 + (1/𝑟) cos𝜃 𝐞2
𝐠3 = 𝑔31𝐠1 + 𝑔32𝐠2 + 𝑔33𝐠3 = 0 + 0 + 𝐠3 = 𝐠3 ∴ 𝐠3 = 𝐞3 ▮ [12.2.4,5]
4) 변환된 성분 구하기: 𝑢𝑖 = 𝑔𝑖𝑗 𝑢𝑗
5) 변환된 tensor 구성함: 𝐮 = 𝑢𝑖 𝐠𝑖 <- covariant → contravariant 의 경우에도 유사 방식으로 진행됩니다.
d) 12.5 Outer product(외적)
∘ 𝐠𝑖 ⨯ 𝐠𝑗 ≡ 𝝐𝑖𝑗𝑘 𝐠𝑘, 𝐚 ⨯ 𝐛 = 𝑎𝑖𝑏𝑗 (𝐠𝑖 ⨯ 𝐠𝑗) = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗 𝐠𝑘 <- 𝝐𝑖𝑗𝑘: 일반 좌표계의 순환 기호 [12.5.2,3]
∘ 𝐠𝑖 ⨯ 𝐠∣ ≡ 𝝐𝑖𝑗𝑘 𝐠𝑘, 𝐚 ⨯ 𝐛 = 𝑎𝑖𝑏𝑗 (𝐠𝑖 ⨯ 𝐠∣) = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗 𝐠k ∴ 일반 좌표계의 vector의 외적: 𝐚 ⨯ 𝐛 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗 𝐠k or 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗 𝐠k [12.5.5,6]
e) 12.6 Triple inner product(삼중 내적)
(𝐚 ⨯ 𝐛) ∙ 𝐜 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗 𝐠𝑘 ∙ 𝑐𝑙 𝐠𝑙 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗𝑐𝑙 𝐠𝑘 ∙ 𝐠𝑙 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗𝑐𝑙 𝛿𝑘𝑙 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗𝑐𝑘 ∴ (𝐚 ⨯ 𝐛) ∙ 𝐜 = 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗𝑐𝑘 or 𝝐𝑖𝑗𝑘 𝑎𝑖𝑏𝑗𝑐𝑘 [12.6.1-3]
∘ Permutation symbol(순환 기호) 정의: 𝝐𝑖𝑗𝑘 ≡ (𝐠𝑖 ⨯ 𝐠𝑗) ∙ 𝐠𝑘 <- 𝐄 = 𝝐𝑖𝑗𝑘 𝐠𝑖 ⊗ 𝐠𝑗 ⊗ 𝐠𝑘의 covariant 성분 [12.6.5]
𝝐𝑖𝑗𝑘 =
⌈ 𝑉𝑔 (123, 231, 312)
┃ -𝑉𝑔 (321, 132, 213) <- 𝑉𝑔: 3개 기저 vector들로 이루어진 평행육면체의 체적 [12.6.8]
⌊ 0 (223, 331 기타)
∘ Reciprocal basis(역기저) vector <- 그림 12.1 참조
𝐠1 ∙ 𝐠1 = 1, 𝐠1 ∙ 𝐠2 = 0, 𝐠1 ∙ 𝐠3 = 0, (<- Kronecker delta) ∴ 𝐠1 = 𝜆(𝐠2 ⨯ 𝐠3), 𝐠1 ∙ 𝐠1 = 𝜆(𝐠2 ⨯ 𝐠3) ∙ 𝐠1 = 𝜆𝑉𝑔 = 1, 𝜆 = 1/𝑉𝑔.
∴ 𝐠1 = (𝐠2 ⨯ 𝐠3)/𝑉𝑔, 𝐠2 = (𝐠3 ⨯ 𝐠1)/𝑉𝑔, 𝐠3 = (𝐠1 ⨯ 𝐠2)/𝑉𝑔 [12.6.15-17]
∘ Reciprocal permutation symbol(역순환 기호): 𝝐𝑖𝑗𝑘 ≡ (𝐠𝑖 ⨯ 𝐠𝑗) ∙ 𝐠𝑘 <- 𝐅 = 𝝐𝑖𝑗𝑘 𝐠𝑖 ⊗ 𝐠𝑗 ⊗ 𝐠𝑘의 contravariant 성분 [12.6.26]
𝝐𝑖𝑗𝑘 =
⌈ 1/𝑉𝑔 (123, 231, 312)
┃-1/𝑉𝑔 (321, 132, 213) <- 𝑉 𝑔: 3개 기저 vector들로 이루어진 평행육면체의 체적 [12.6.30]
⌊ 0 (223, 331 기타)
f) 12.7 수학적 유도 과정
∘ Permutation symbol(순환 기호) 관계식: 𝝐𝑖𝑗𝑘 = 𝑉𝑔 𝑒𝑖𝑗𝑘 <- Cartesian 좌표계의 순환 기호의 사용 가능 [12.7.1]
∘ Triple inner product(삼중 내적) 값의 유도: (𝐠𝑖 ⨯ 𝐠𝑗 ∙ 𝐠𝑘)(𝐠p ⨯ 𝐠q ∙ 𝐠r) = 𝝐𝑖𝑗𝑘 𝝐𝑝𝑞𝑟 <- ※ [6.5.25] 참조 [12.7.2]
𝝐𝑖𝑗𝑘 𝝐𝑝𝑞𝑟 =
∣ 𝐠𝑖 ∙ 𝐠𝑝 𝐠𝑖 ∙ 𝐠𝑞 𝐠𝑖 ∙ 𝐠𝑟 ∣ ∣ 𝑔𝑖𝑝 𝑔𝑖𝑞 𝑔𝑖𝑟 ∣
∣ 𝐠𝑗 ∙ 𝐠𝑞 𝐠𝑗 ∙ 𝐠𝑞 𝐠j ∙ 𝐠r ∣ = ∣ 𝑔𝑗𝑝 𝑔𝑗𝑞 𝑔𝑗𝑟 ∣ = det [𝐠𝑖𝑗], 𝑔 ≡ det [𝐠𝑖𝑗] [12.7.4,5]
∣ 𝐠𝑘 ∙ 𝐠𝑝 𝐠𝑘 ∙ 𝐠𝑞 𝐠𝑘 ∙ 𝐠𝑟 ∣ ∣ 𝑔𝑘𝑝 𝑔𝑘𝑞 𝑔𝑘𝑟 ∣
basis vector (𝝐123)2 = det [𝐠] (𝑖,𝑗 = 1,2,3) = 𝑔, 𝝐123 = √ 𝑔 = 𝑉𝑔 ∴ 𝝐𝑖𝑗𝑘 = 𝑉𝑔 𝑒𝑖𝑗𝑘 = √ 𝑔 𝑒𝑖𝑗𝑘 [12.7.6-8]
∘ Reciprocal permutation symbol(역순환 기호): 𝝐𝑖𝑗𝑘 = 𝐠𝑖 ⨯ 𝐠𝑗 ∙ 𝐠𝑘, 𝝐𝑖𝑗𝑘 = (1/√ 𝑔) 𝑒𝑖𝑗𝑘 <- 역기저 vector 참조 [12.7.13-19]
g) 12.8 Eigenvalue(고유값) 관련
(𝐀 - λ𝐈) ∙ 𝐱 = 0 λ: eigenvalue(고유값), 𝐱: eigenvector(고유 vector) , 𝐈: identity vector(단위 vector) [12.8.1]
det (𝐀 - λ𝐈) = 0 [12.8.2]
λ3 - 𝐼 λ2 + 𝐼𝐼 λ2 - 𝐼𝐼𝐼 = 0 <- 𝐼, 𝐼𝐼, 𝐼𝐼𝐼: invariant scalars [12.8.3]
𝐼 = tr𝐀 = 𝐴𝑖.𝑖 𝐼𝐼 = 1/2{(tr𝐀 )2 - (tr(𝐀 2)} = 1/2 {(𝐴𝑖.𝑖 𝐴𝑗.𝑗 - 𝐴𝑖.𝑗 𝐴𝑖.𝑗)} 𝐼𝐼𝐼 = det 𝐀 = 𝑒𝑖𝑗𝑘 𝐴𝑖.1 𝐴𝑗.2 𝐴𝑘.3 [12.8.4-6]
|
|
|





































