|
김관석
|
2019-06-16 16:51:45, 조회수 : 1,176 |
- Download #1 : dff_1_3.jpg (47.8 KB), Download : 1
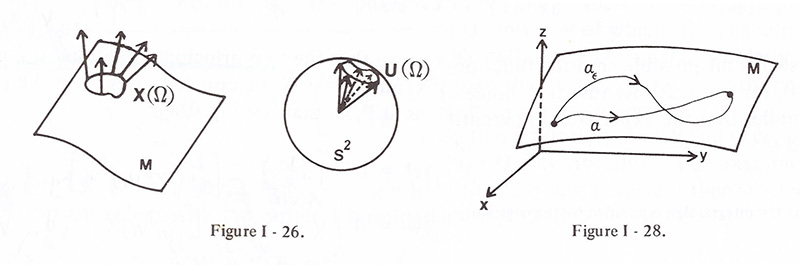

6. Gauss Curvature II <- Figure I-26 참조
∘ Definition I-4
𝐤1과 𝐤2가 곡면 𝐌의 한 점 𝐏의 normal curvature 𝐤n(𝐯)의 최대값과 최소값이라면, 𝐤1과 𝐤2를 principal curvatures 라
하며 해당 방향을 principal directions 이라 하며, 곱인 𝐊 = 𝐊(𝐏) = 𝐤1𝐤2는 𝐏에서의 𝐌의 Gauss curvature 라 부른다.
∘ Theorem I-5
𝐌의 어떤 점 𝐏의 Gauss curvature : 𝐊(𝐏) = 𝐿/𝑔 로 주어진다. <- 𝐿 = det (𝐿𝑖𝑗), 𝑔 = det (𝑔𝑖𝑗)
Proof. 우리는 𝑔𝑖𝑗v𝑖v𝑗 = 1 라는 제한된 식을 extremize(極値化)함으로써 증명을 유도하려고 합니다.
𝐤 = 𝐤n(𝐯) = 𝐿𝑖𝑗v𝑖v𝑗/𝑔𝑚𝑛v𝑚v𝑛 <- 𝐯: non-zero vectors of 𝐓𝑝𝐌; 𝐯 = v𝑖𝐗𝑖: principal direction vector, ∂𝐤/∂v1 = ∂𝐤/∂v2 = 0
Let f(x1, x2) = a𝑖𝑗x𝑖x𝑗 <- quadratic form, (a𝑖𝑗): real symmetric n X n matrix: a𝑖𝑗 = a𝑖𝑗, Then ∂f/∂x𝑟 = 2a𝑟𝑗x𝑗, r = 1,2. ∴
[d[f(x)/g(x)]/dx = [f'(x)g(x)- f(x)g'(x)]/g(x)2]→ ∂𝐤/∂v𝑟 = (2𝑔𝑚𝑛v𝑚v𝑛𝐿𝑟𝑗v𝑗 - 2𝐿𝑖𝑗v𝑖v𝑗𝑔𝑟𝑛v𝑛)/(𝑔𝑚𝑛v𝑚v𝑛)2, r = 1,2
[분자의 𝐿𝑖𝑗v𝑖v𝑗↦ 𝐤𝑔𝑚𝑛v𝑚v𝑛, 분자 분모를 정리]→ ∂𝐤/∂v𝑟 = [2(𝐿𝑟𝑗 - 𝐤𝑔𝑟𝑗)v𝑗]/𝑔𝑚𝑛v𝑚v𝑛, r = 1,2
At an extreme value we must have (𝐿𝑖𝑗 - 𝐤𝑔𝑖𝑗)v𝑗 = 0, 𝑖 = 1,2. then det(𝐿𝑖𝑗 - 𝐤𝑔𝑖𝑗) = 0. <- v𝑗: non-zero vector; why? [6-24]
𝑔 = det (𝑔𝑖𝑗) = 𝑔11𝑔22 - (𝑔11)2, 𝐿 = 𝐿11𝐿22 - (𝐿11)2; 𝐤2, 𝐤, constant에 대해 (𝐤 - 𝐤1)(𝐤 - 𝐤2) = 0 방식으로 전개합니다.
𝐤2𝑔 - 𝐤(𝑔11𝐿22 + 𝑔22𝐿11 - 2𝑔12𝐿12) + 𝐿 = 0 or 𝐤2 - 𝐤(𝑔11𝐿22 + 𝑔22𝐿11 - 2𝑔12𝐿12)/𝑔 + 𝐿/𝑔 = 0, ∴ 𝐊(𝐏) = 𝐤1𝐤2 = 𝐿/𝑔 ▮ *
∘ Gauss curvature의 두 principal direction은 서로 직교한다.
Proof. 점 𝐏의 두 non-zero principal direction vector를 각각 𝐯 = v𝑖𝐗𝑖, 𝐰 = w𝑖𝐗𝑖 라고 합시다.
By Eq. (24), (𝐿𝑖𝑗 - 𝐤1𝑔𝑖𝑗)v𝑗 = 0, (𝐿𝑖𝑗 - 𝐤2𝑔𝑖𝑗)w𝑗 = 0, 𝑖 = 1,2; [𝑖 ⇄ 𝑗, 𝑔𝑖𝑗 = 𝑔𝑗𝑖] → 𝐿𝑖𝑗v𝑖 = 𝐤1𝑔𝑖𝑗v𝑖, 𝑖 = 1,2 [6-25]
By Eq. (24) (25), (𝐤1 - 𝐤2)𝑔𝑖𝑗v𝑖w 𝑗 = 0. ∴𝑔𝑖𝑗v𝑖w 𝑗 = 𝐯 ∙ 𝐰 = 0. 만일 𝐤1 ≠ 𝐤2 이면, 두 principal directions은 서로 직교한다.
만일 𝐤1 = 𝐤2 이면, 우리는 서로 직교하는 두 direction을 선택해서 principal directions이라고 부릅니다. ▮
∘ Sphere mapping or Gauss mapping
𝐏 = 𝐗 (u10, u20) 그리고 𝛺: neighborhood of (u10, u20), 𝐗: one-to-one, continuous inverse 𝐗(𝛺)→ 𝛺 라고 가정한다면,
𝐗(𝛺)의 각 점 𝐗 (u1, u2)으로, E3의 원점으로 pararell-translated normal vector 𝐔 (u1, u2)를 관련시킬 수 있습니다.
∥𝐔∥= 1 이므로, 그 translated vector는 unit sphere 𝐒2의 한점관 연관시켜 볼 수 있는데, 이러한 𝐗(𝛺)→ 𝐒2 mapping을
Sphere mapping 또는 Gauss mapping라 부르며. 𝐔(𝛺)는 𝐗(𝛺)의 spherical normal image라 부르기도 합니다.
𝐔는 sphere에 수직하므로, 𝐒2의 𝐔(u1, u2)의 tangent plane 𝐓u𝐒2는 𝐗(u1, u2)의 tangent plane 𝐓x𝐌과 평행합니다.
∴ 𝐔 = ∓ (𝐔1 ⨯ 𝐔2) /∥𝐔1 ⨯ 𝐔2∥ or 𝐔 ∙ 𝐔1 ⨯ 𝐔2 = ∓∥𝐔1 ⨯ 𝐔2∥.
∘ Area 𝐔(𝛺) = ∓ ∬𝛺∥𝐔1 ⨯ 𝐔2∥du1du2 = ∬𝛺 𝐔 ∙ 𝐔1 ⨯ 𝐔2 du1du2, 𝐗(𝛺) = ∓ ∬𝛺∥𝐗1 ⨯ 𝐗2∥du1du2 = ∬𝛺 𝐔 ∙ 𝐗1 ⨯ 𝐗2 du1du2
𝐊(𝐏) = lim𝛺 → (u01, u02) [Area 𝐔(𝛺)/Area 𝐗(𝛺)] [6-26]
Area 𝐔(𝛺) ≈ (𝐔 ∙ 𝐔1 ⨯ 𝐔2)(𝐏) A(𝛺), 𝐗(𝛺) ≈ (𝐔 ∙ 𝐗1 ⨯ 𝐗2)(𝐏) A(𝛺) ∴ Area 𝐔(𝛺)/𝐗(𝛺) ≈ (𝐔 ∙ 𝐔1 ⨯ 𝐔2 / 𝐔 ∙ 𝐗1 ⨯ 𝐗2) (𝐏)
∘ Lemma (보조 정리) I-6
𝐔1 ⨯ 𝐔2 = 𝐊 (𝐗1 ⨯ 𝐗2)
Proof. Define the functions 𝐿𝑖𝑗(u1, u2) 𝐿𝑖𝑗 ≡ 𝐿𝑗𝑘 𝑔𝑘𝑖, 𝑖,𝑗 =1,2 [6-27]
𝐿𝑖𝑗 𝑔𝑖𝑚 = 𝐿𝑗𝑘 𝑔𝑘𝑖𝑔𝑖𝑚 = 𝐿𝑗𝑘 𝛿𝑘𝑚 = 𝐿𝑗𝑚; 𝐔 ∙ 𝐔 = 1, ∴ 𝐔 ∙ 𝐔𝑗 = 0; 𝐔𝑗 = a𝑟𝑗 𝐗𝑟, 𝑗 =1,2 <- linear combination of 𝐗1 and 𝐗2
𝐔 ∙ 𝐗𝑘 = 0 → 𝐔𝑗 ∙ 𝐗𝑘 + 𝐔 ∙ 𝐗𝑗𝑘 = 0 <- differentiated by u𝑗; ∴ 𝐔𝑗 ∙ 𝐗𝑘 = - 𝐔 ∙ 𝐗𝑗𝑘 = -𝐿𝑗𝑘 = a𝑟𝑗 𝐗𝑟 ∙ 𝐗𝑘 = a𝑟𝑗 𝑔𝑟𝑘, 𝑗,𝑘 = 1,2
<- by eq. 20; [양변에 𝑔𝑘𝑖를 곱하고 sum over k]→ - 𝑔𝑘𝑖𝐿𝑗𝑘 = a𝑟𝑗 𝑔𝑟𝑘𝑔𝑘𝑖 = a𝑟𝑗 𝛿𝑖𝑟 = a𝑖𝑗, ∴ a𝑖𝑗 = - 𝐿𝑖𝑗 <- by eq. 27;
∴ 𝐔𝑗 = - 𝐿𝑖𝑗 𝐗𝑖, 𝑗 =1,2 <- the equation of Weingarten [6-28]
𝐔1 ⨯ 𝐔2 = (- 𝐿𝑖1𝐗𝑖) ⨯ (- 𝐿𝑘2𝐗𝑘) = (𝐿11𝐗1 + 𝐿21𝐗2) ⨯ (𝐿12𝐗1 + 𝐿22𝐗2) = (𝐿11𝐿22 - 𝐿21𝐿12) (𝐗1 ⨯ 𝐗2) = det (𝐿𝑖𝑗) (𝐗1 ⨯ 𝐗2)
<- 𝐗𝑖 ⨯ 𝐗𝑖 = 𝟎, 𝐗𝑖 ⨯ 𝐗𝑗 = - 𝐗𝑗 ⨯ 𝐗𝑖; [det(𝐀𝐁) = det(𝐀)det(𝐁); det(𝐀-1) = 1/det(𝐀): det(𝐀) is non-zero, iff, 𝐀 is invertible.]
det(𝐿𝑖𝑗) = det(𝐿𝑗𝑘𝑔𝑘𝑖) = det(𝐿𝑗𝑘)det(𝑔𝑘𝑖) = det(𝐿𝑗𝑘)/det(𝑔𝑘𝑖) = 𝐿/𝑔 = 𝐊. ▮
7. Geodesics ** <- Figure I-28 참조
∘ 일반적으로 곡면 𝐌 위 곡선 𝛂은 두가지 이유로 curvature를 갖습니다. 첫째는 곡면 자체가 3차원의 공간 속에서 굽은 것으로
본질적으로는 앞에서 논의된 normal curvature 입니다. 둘째는 𝐌이 곡면이든 아니든 𝛂가 𝐌에 대해 상대적으로 굽은 정도로
이를 geodesic curvature 라 부르며, 아래와 같이 정의합니다.
∘ 𝛂(s) <- s: arc length; 𝛂' ∙ 𝛂' = 1, ∴ 𝛂" ∙ 𝛂' = 0; 𝛂" = 𝛂"tan + 𝛂"nor = (u𝑟" + 𝛤𝑟𝑖𝑗 u𝑖'u𝑗')𝐗𝑟 + (𝐿𝑖𝑗 u𝑖'u𝑗')𝐔 <- by eq. (18)
𝛂"tan ∙ 𝐔 = 0 and 𝛂"tan ∙ 𝛂' = (𝛂"tan + 𝛂"nor) ∙ 𝛂' = 𝛂" ∙ 𝛂' = 0 이므로, 𝛂"tan는 다음 식의 the geodesic normal vector 인,
𝐰 = 𝐔 ⨯ 𝛂' (a vector tangent to 𝐌)와 비례하는데. 그 propotionality factor를 geodesic curvature 라고 부릅니다.
∘ Definition I-7
𝛂 = 𝛂(s)가 s가 호의 길이인 𝐌의 곡선일 때, 𝛂(s)에서의 geodesic curvature 는 다음 방정식의 함수 𝐤g = 𝐤g(s)이다.
𝛂"tan = 𝐤g 𝐰 = 𝐤g 𝐔 ⨯ 𝛂' [7-30]
∴ 𝐤g = 𝐔 ∙ 𝛂' ⨯ 𝛂" <- geodesic curvature 𝐤g = 𝛂"tan∙ 𝐰 = 𝛂" ∙ 𝐰 = 𝛂" ∙ 𝐔 ⨯ 𝛂' <- 삼중 내적의 순환 [7-31]
∘ Definition I-8
𝛂 = 𝛂(s)가 s가 호의 길이인 𝐌의 곡선일 때, 만일 𝛂가 모든(every) 점에서 𝛂"tan = 𝟬 (동등하게 𝛂" = 𝛂"nor) 이라면
𝛂를 하나의 geodesic 이라고 부른다.
∴ 𝛂"tan = u𝑟" + 𝛤𝑟𝑖𝑗 u𝑖'u𝑗' = 0, 𝑟 = 1,2, 𝐤g = 𝐔 ∙ 𝛂'⨯ 𝛂" = 0 <- a geodesic, if and onky if, [7-32ab]
∘ Christoffel symbols of the second kind and the first kind
Eq. (17) [𝐗𝑖𝑗 = 𝛤𝑟𝑖𝑗𝐗𝑟 + 𝐿𝑖𝑗𝐔, 𝑖,𝑗 = 1, 2]에서 정의된 𝛤𝑟𝑖𝑗를 Christoffel symbols of the second kind 라고 부릅니다.
또한 𝛤𝑖𝑗𝑘 = 𝛤𝑟𝑖𝑗𝑔𝑟𝑘 𝑖,𝑗,𝑘 = 1,2 로 정의합니다. <- 𝛤𝑖𝑗𝑘: Christoffel symbols of the first kind [7-33]
𝐗𝑖𝑗 ∙ 𝐗𝑘 = 𝛤𝑟𝑖𝑗 𝐗𝑟 ∙ 𝐗𝑘 = 𝛤𝑟𝑖𝑗 𝑔𝑟𝑘 = 𝛤𝑖𝑗𝑘 -> ※ 𝛤𝑟𝑖𝑗= 𝛤𝑟𝑗𝑖, 𝛤𝑖𝑗𝑘= 𝛤𝑗𝑖𝑘, 𝛤𝑚𝑖𝑗= 𝛤𝑖𝑗𝑘 𝑔𝑘𝑚 by eq. (17,12) [7-34]
∂𝑔𝑖𝑘/∂u𝑗 = (∂ /∂u𝑗)(𝐗𝑖 ∙ 𝐗𝑘) = 𝐗𝑖𝑗 ∙ 𝐗𝑘 + 𝐗𝑘𝑗 ∙ 𝐗𝑖 = 𝛤𝑖𝑗𝑘 + 𝛤𝑘𝑗𝑖
∂𝑔𝑖𝑘/∂u𝑗 = 𝛤𝑖𝑗𝑘 + 𝛤𝑘𝑗𝑖, ∂𝑔𝑗𝑖/∂u𝑘 = 𝛤𝑗𝑘𝑖 + 𝛤𝑖𝑘𝑗, ∂𝑔𝑘𝑗/∂u𝑖 = 𝛤𝑘𝑖𝑗 + 𝛤𝑗𝑖𝑘 [7-35]
∴ 𝛤𝑖𝑗𝑘 = 1/2 (∂𝑔𝑖𝑘/∂u𝑗 + ∂𝑔𝑘𝑗/∂u𝑖 - ∂𝑔𝑗𝑖/∂u𝑘) <- Christoffel symbols of the first kind [7-36]
∴ 𝛤𝑟𝑖𝑗 = (1/2) 𝑔𝑘𝑟 (∂𝑔𝑖𝑘/∂u𝑗 + ∂𝑔𝑘𝑗/∂u𝑖 - ∂𝑔𝑗𝑖/∂u𝑘) <- Christoffel symbols of the second kind [7-37]
Eq.(32a)(37)로 extrinsic한 정의의 Christoffel symbol과 geodesic의 intrinsic 해법이 가능한 것을 알 수 있습니다!
∘ Christoffel symbols 계산 <- 𝑔𝑖𝑗 = 𝐗𝑖 ∙ 𝐗𝑗, 𝑔 = det (𝑔𝑖𝑗) = 𝐸𝐺 - 𝐹2, 𝑔𝑖𝑗𝑔𝑗𝑘 = 𝛿𝑘𝑖, 𝑔11= 𝑔22/𝑔, 𝑔12= 𝑔21= -𝑔12/𝑔, 𝑔22= 𝑔11/𝑔
Orthogonal coordinates 直交 座標系: 𝐹 = 𝑔12= 𝑔21= 0, 𝑔12= 𝑔21= 0, 𝑔11= 𝐺/𝐸𝐺 = 1/𝐸 = 1/𝑔11, 𝑔22= 𝐸/𝐸𝐺 = 1/𝐺 = 1/𝑔22
𝛤𝑟𝑖𝑗 = (1/2𝑔𝑟𝑟)(∂𝑔𝑖𝑟/∂u𝑗 + ∂𝑔𝑟𝑗/∂u𝑖 - ∂𝑔𝑗𝑖/∂u𝑟) (no sum) <- replacing 𝑘 by 𝑟 [7-38]
(Case 1) For 𝑗 = 𝑟: 𝛤𝑟𝑖𝑟 = (1/2𝑔𝑟𝑟) ∂𝑔𝑟𝑟/∂u𝑖 (no sum) [7-39a]
(Case 2) For 𝑖 = 𝑗 ≠ 𝑟: 𝛤𝑟𝑖𝑖 = (1/2𝑔𝑟𝑟)(- ∂𝑔𝑖𝑖/∂u𝑟) (no sum) <- 𝑔𝑖𝑟= 𝑔𝑗𝑟= 0 [7-39b]
(Case 3) (in dimension > 2) For 𝑖, 𝑗, 𝑟 all distinct: 𝛤𝑟𝑖𝑗 = 0 <- 𝑔𝑖𝑗= 𝑔𝑖𝑟= 𝑔𝑗𝑟= 0 [7-39c]
(in dimension 2) 𝛤111= 𝐸u/2𝐸, 𝛤222= 𝐺v/2𝐺, 𝛤112= 𝛤121= 𝐸v/2𝐸, 𝛤212= 𝛤221= 𝐺u/2𝐺, 𝛤122= -𝐺u/2𝐸<, 𝛤211= -𝐸v/2𝐺 [7-40]
∘ Example 17. Cartesian 좌표계의 평면
ds2 = du2 + dv2, 𝐸 = 𝐺 = 1, u"= v"= 0; u = as + b, v = cs + d, ∴ geodesics: straight lines(直線) ▮
∘ Example 18. Geographic(地理) 좌표계의 구
𝐗(u, v) = (R cos u cos v, R cos u sin v, R sin v), 𝐸 = R2cos v2, 𝐹 = 0 , 𝐺 = R2,
𝐗1 = (-R sin u cos v, R sin u sin v, 0), 𝐗2 = (-R cos u sin v, R cos u cos v, R cos v),
ds2 = R2cos2v du2 + R2dv2, 𝛤112= 𝛤121= 𝐸v/2𝐸 = -tan v, 𝛤211= -𝐸v/2𝐺 = sin v cos v,
(Geographic 좌표계 구의 geodesics이 great circles(大圓)이라는 증명은 나중에 나옵니다. <- Ex. 12, 14 참조)
∘ Example 19. Polar(極) 좌표계의 평면
𝐗(r, 𝜃) = (rcos𝜃, rsin𝜃, 0), 𝐗1 = (cos𝜃, sin𝜃, 0), 𝐗2 = (-rsin𝜃, rcos𝜃, 0), 𝐸 = 1, 𝐹 = 0, 𝐺 = r2; (u, v)→ (r, 𝜃) in Eq. (40)
ds2 = dr2 + r2d𝜃2, 𝛤212= 𝛤221= 1/r, 𝛤122= -r; applying Eq. (32a) [ur" + 𝛤𝑟𝑖𝑗u𝑖'u𝑗' = 0, r=1,2 u1= r, u2= 𝜃]→
d2r/ds2 - r (d𝜃/ds)2 = 0, d2𝜃/ds2 + 2/r (dr/ds)(d𝜃/ds) = 0 [7-41ab]
If we divide Eq. (41b) by 𝜃'= d𝜃/ds, then 1/𝜃'(d𝜃'/ds) + 2/r(dr/ds) = 0, [integrated to s]→ ln ∣𝜃'∣ + ln r2 = c.
[expoentiationg]→ ∣r2𝜃'∣ = ec or r2 d𝜃/ds = h h: non-zero constant [7-42]
[deviding Eq.(6) by ds2] → 1 = (dr/ds)2 + r2(d𝜃/ds)2 = (dr/ds)2 + h2/r2 [7-43]
dr/ds = ∓ 1/r(r2 - h2)1/2, [by eq. (40)]→ d𝜃/dr = ∓ h/[r(r2-h2)1/2] = ∓ d(cos-1 h/r)/dr
h/r = cos(𝜃 - 𝜃0) <- h: 원점에서 직선까지 수직거리, 𝜃0: 𝜃 = 0 에서 원점에서 직선까지의 수직 교차점까지의 각 [7-44]
그러므로 이 geodesic은 점 𝐏(r, 𝜃)와 𝐀(h, 𝜃0)를 연결하는 직선 𝐏𝐀↔의 방정식입니다. <- ∠𝐏𝐎𝐀 = 𝜃 - 𝜃0 ▮
∘ Theorem I-9
𝛂 = 𝛂(s)가, a≤s≤b, 𝐌 위의 s가 호의 길이인 곡선일 때, 만일 𝛂가 두 끝점을 연결하는 곡면 𝐌 위의 가장 짧은 곡선이라면,
𝛂는 한 geodesic이다.
Proof. 𝛂(s) = 𝐗(u1(s), u2(s)), length of 𝛂𝜖(s) ≧ length of 𝛂(s),
U𝑖(s, 𝜖) = u𝑖(s) + 𝜖v𝑖(s) for 𝑖=1,2, a≤s≤b, v𝑖: smooth function v𝑖(a)= v𝑖(b)= 0, 𝑖=1,2, 임의의 (U1, U2) in the domain of 𝐗
For each 𝜖, 𝛂𝜖(s) = 𝐗(U1(s, 𝜖), U1(s, 𝜖)) is a slight variation. [Figure I-28]; 이제 L(𝜖)를 𝛂𝜖의 길이라고 합시다.
L(𝜖) = ∫ab𝜆(s, 𝜖)ds, <- 𝜆(s, 𝜖) = [𝑔𝑖𝑗(U1,U2) ∂U𝑖/∂s, ∂U𝑗/∂s]1/2; the minimality of L(0) → L'(0) = ∫ab ∂𝜆(s,0)/∂𝜖 ds = 0
∂𝜆(s,𝜖)/∂𝜖 = 1/2𝜆[(∂𝑔𝑖𝑗)/∂𝜖)(∂U𝑖/∂s)(∂U𝑗/∂s) + 2𝑔𝑖𝑗(∂U𝑖/∂s)(∂2U𝑗/∂s∂𝜖)] <- 𝜆=√ F, 𝜆'=(1/2𝜆)F'; 𝑔𝑖𝑗= 𝑔𝑗𝑖
L'(0) = (1/2)∫ab (∂𝑔𝑖𝑗/∂U𝑘)v𝑘U𝑖'U𝑗' + 2𝑔𝑖𝑘U𝑖'v𝑘') ds = 0 <- 𝜖 = 0, 𝛂0(s) = 𝛂(s), 𝜆(s, 0) = 1; ∂U𝑗/∂𝜖 = v𝑗
괄호안 둘째항의 적분: [∫ udv = uv- ∫ vdu], u: 2𝑔𝑖𝑘U𝑖', dv: v𝑘'ds, du: ∂/∂s[2𝑔𝑖𝑘U𝑖']ds, v = ∫ dv = ∫ v𝑘'ds = v𝑘,
uv = 2𝑔𝑖𝑘U𝑖'v𝑘 ∣ba = 0 (∵ v𝑘(a) = v𝑘(b) = 0), ∴ [∫ udv = - ∫ vdu = - 2∂(𝑔𝑖𝑘U𝑖'v𝑘)/∂s ds
L'(0) = (1/2)∫ab[(∂𝑔𝑖𝑗/∂U𝑘)U𝑖'U𝑗' - 2∂(𝑔𝑖𝑘U𝑖')/∂s] v𝑘 ds = 0
∴ 1/2(∂𝑔𝑖𝑗/∂U𝑘)U𝑖'U𝑗' - ∂(𝑔𝑖𝑘U𝑖')/∂s = 0, 𝑘 = 1,2 → 이하는 이로부터 Eq. (32a)를 추론합니다.
0 = 1/2(∂𝑔𝑖𝑗/∂U𝑘)U𝑖'U𝑗' - (∂𝑔𝑖𝑘/∂U𝑗)U𝑖''U𝑗'- 𝑔𝑚𝑘u𝑚" = [1/2(𝛤𝑖𝑘𝑗 + 𝛤𝑗𝑘𝑖) - (𝛤𝑘𝑗𝑖 + 𝛤𝑖𝑗𝑘)]U𝑖'U𝑗' - 𝑔𝑚𝑘u𝑚"
[𝛤𝑖𝑘𝑗U𝑖'U𝑗' = 𝛤𝑗𝑘𝑖U𝑖'U𝑗'] (dummi index 교환); 𝛤𝑗𝑘𝑖 = 𝛤𝑘𝑗𝑖; ∴ 𝑔𝑚𝑘u𝑚" + 𝛤𝑖𝑗𝑘U𝑖'U𝑗' = 0; 양변에 𝑔𝑘r 곱하고 k에 대해 합산을 하면,
𝑔𝑚𝑘𝑔𝑘ru𝑚" + 𝛤𝑖𝑗𝑘𝑔𝑘rU𝑖'U𝑗' = 0, 𝜎𝑚ru𝑚" + 𝛤 r 𝑖𝑗U𝑖'U𝑗' = 0, ur" + 𝛤 r 𝑖𝑗U𝑖'U𝑗' = 0, r = 1,2; ∴ 𝛂는 하나의 geodesic입니다. ▮
∘ Theorem I-10
𝐌의 점 𝐏와 그 곳의 unit tangent vector 𝐯가 주어지면, 𝛂(0) = 𝐏 그리고 𝛂'(0) = 𝐯인 유일한 geodesic 𝛂(s)가 존재한다.
Proof. 𝐏 = 𝐗(u01, u01), 𝐯 = v𝑖𝐗𝑖(u01, u01) 이라고 하면 geodesic의 정의 Eq. (32a)에 따라 유일한 function ur(s)는,
u𝑟" + 𝛤𝑟𝑖𝑗 u𝑖'u𝑗' = 0, ur = ur0, ur'(0) = v' for r = 1,2 <- 𝛂(s) = 𝐗(u1(s), u2(s)), s: arc length
f(s) = ∥𝛂'(s)∥2 = 𝑔𝑖𝑗 u𝑖'u𝑗' = constant C <- ds2 by eq. (6), the first fundamental form; f(0): unit length
f'(s) = (∂𝑔𝑖𝑗/∂u𝑘)u𝑖'u𝑗'u𝑘' + 𝑔𝑖𝑗 u𝑖"u𝑗' + 𝑔𝑖𝑗 u𝑖'u𝑗" = (𝑔𝑗𝑟𝛤𝑟𝑖𝑘 + 𝑔𝑖𝑟𝛤𝑟𝑗𝑘)u𝑖'u𝑗'u𝑘' + 𝑔𝑖𝑗 u𝑖"u𝑗' + 𝑔𝑖𝑗 u𝑖'u𝑗"
= 𝑔𝑖𝑟u𝑖'(u𝑟" + 𝛤𝑟𝑗𝑘 u𝑗'u𝑘') + 𝑔𝑟𝑗u𝑗'(u𝑟" + 𝛤𝑟𝑖𝑘 u𝑖'u𝑘') = 0, and so f(s) ≡ 1. <- unit tangent vector
즉, Geodesic 필요충분조건식 Eq. (32a)을 적용하면 metric form이 성립하고, 그 역도 성립하므로 증명이 완료됩니다. ▮
∘ Exercise I-7-12. Sppose 𝐌 has metric form ds2 = 𝐸 du2 + 𝐺 dv2 with 𝐸v = 𝐺v = 0.
(a) Verify that the only non-zero Christoffel symbol 𝛤𝑟𝑖𝑗 are 𝛤111 = 𝐸u /2𝐸, 𝛤212 = 𝛤221 = 𝐺u /2𝐺, 𝛤122 = - 𝐺u /2𝐸. Solution. Eq. (40)
(b) Show that a geodesic on 𝐌 satisfies v" + 𝐺u /𝐺 u' v' = 0 and intergrate this equation to obtain 𝐺v' = h (a non-zero constant)
Solution. u𝑟" + 𝛤𝑟𝑖𝑗 u𝑖'u𝑗' = 0, 𝑟 = 1,2, Hence v " + 2𝛤212u'v' = 0. ∴ v" + 𝐺u /𝐺 u'v' = 0. Again, d(𝐺v')/𝐺ds = v" + (𝐺u /𝐺)u'v' = 0.
Therefore d(𝐺v')/ds = 0, and 𝐺v' = h, h = non-zero constant.
(c) Refering to Example 19, combine 𝐺v' = h with 𝐸 (u')2 + 𝐺 (v')2 = 1 to obtain dv/du = ∓ h√ 𝐸 /{√ 𝐺 √ (𝐺 - h2)}. [7-45]
Solution. dv/dh = h/𝐺. 1 = 𝐸(du/ds)2 + 𝐺(du/ds)2= 𝐸(du/ds)2 + 𝐺(h/𝐺)2= 𝐸(du/ds)2 + h2/𝐺. Hence du/ds = ∓ √ {(1 - h2/𝐺)/𝐸},
dv/du = ∓ h/𝐺 √ {E/(1 - h2/𝐺)} = ∓ h√ 𝐸 /{√ 𝐺 √ (𝐺 - h2)}. ▮
∘ Exercise I-7-14. If 𝐌 has metric ds2 = 𝐸 du2 + 𝐺 dv2 with 𝐸u = 𝐺u = 0. a geodesic on 𝐌 satisfies du/dv = ∓ h√ 𝐺 /√ 𝐸 √ (𝐸 - h2).
(A proof is immediately obtained if in Exercise 12 we Intechange u with v, 𝐸 with 𝐺, and 1 with 2.)
(a) Show that a geodesic on the sphere satisfies du/dv = h sec2v /√ (R2 - h2 sec2v) = h sec2v /√ (R2 - h2 - h2 tan2v). h: const.
Solution. du/dv = ∓ h√ 𝐺 /{√ 𝐸 √ (𝐸 - h2)} 𝐸u' = h, 𝐸 = R2 cos2 v, 𝐺 = R2,
du/dv = ∓ h√ 𝐺 /√ 𝐸 √ (𝐸 - h2) = hR / (R cos v √ (R2 cos v - h2) = h sec2v /√ (R2 - h2 sec2v) = h sec2v /√ (R2 - h2 - h2 tan2v).
(b) By means of the substitution w = h tan v, intergrate the above equation to obtain cos(u - u0) + 𝛾 tan v = 0, u0), 𝛾 = constants. [46]
[Use ∫ (a2 - x2)-1/2 dx = - cos-1 (x/a) + c.]
Solution. dw = h sec2 v dv, u = ∫ {h sec2 v / √ (r2 - h2 - h2 tan2} dv = - ∫ {-1/√ R2 - h2 - w2)} dw = - cos-1(w /√ {R2 - h2)} + u0.
Therefore cos (u - u0) = w /√ {R2 - h2) = h tan v /√ {R2 - h2). Let 𝛾 = -h /√ {R2 - h2) be. Then we have cos (u - u0) + 𝛾 tan v = 0.
(c) Show that Eq. (46), when reexpressed in terms of Cartesian coordinates, x = R cos u cos v, y = R sin u cos v, z = R sin v
is a linear equation of the form 𝛼x + 𝛽y + 𝛾z = 0, and so represednts a plane pf the sphere through the orgin, i.e., a great circle.
Solution. By multiplying R cos v, R cos v cos (u - u0) + 𝛾 cos v tan v = 0, R cos v (cos u cos u0 + sin u sin u0) + 𝛾 sin v = 0.
Hence if 𝛼 = cos u0, 𝛽 = sin u0, then we have 𝛼x + 𝛽y + 𝛾z = 0. (이는 𝐧 (𝛼, 𝛽, 𝛾)과 직교하면서 원점을 지나는 평면 𝐏 (z,y,z)입니다.
즉, 𝐧 ∙ 𝐏 = 0. 따라서 지리적(geographical) 좌표계의 geodesic은 대원(great circle)의 일부입니다.) ▮
p.s. determinant는 선형독립 여부, 역행렬 존재 여부, 삼중내적의 부피 및 Gauss curvature 산정의 '결정자'-google-임. ('행렬식'은 비추천)
* ▮ 'the proof is complete ' 증명이 완료됨을 나타내는 기호
** geodesic: 대한수학회의 측지선(測地線), 물리학회의 지름길인데, 여기서는 측지선/영어로 표기 |
|
|



















